Причинно-следственный график

В статистике, эконометрике, эпидемиологии, генетике и смежных дисциплинах причинные графы (также известные как диаграммы путей , причинные байесовские сети или DAG ) представляют собой вероятностные графические модели, используемые для кодирования предположений о процессе генерации данных.

Причинно-следственные графы можно использовать для связи и вывода. Они дополняют другие формы причинных рассуждений, например, использование обозначения причинного равенства . Будучи средством коммуникации, графики обеспечивают формальное и прозрачное представление причинно-следственных предположений, которые исследователи могут захотеть передать и защитить. В качестве инструментов вывода графики позволяют исследователям оценить величину эффекта на основе неэкспериментальных данных. ^[1]^[2]^[3]^[4]^[5] получить проверяемые последствия закодированных предположений, ^[1]^[6]^[7]^[8] тест на внешнюю валидность, ^[9] и управлять недостающими данными ^[10] и предвзятость отбора. ^[11]

Причинно-следственные графы впервые были использованы генетиком Сьюэллом Райтом. ^[12] в рубрике «путевые диаграммы». Позже они были приняты социологами. ^[13]^[14]^[15]^[16]^[17]^[18] и, в меньшей степени, экономистами. ^[19] Эти модели изначально ограничивались линейными уравнениями с фиксированными параметрами. Современные разработки расширили графические модели до непараметрического анализа и, таким образом, достигли общности и гибкости, которые преобразовали причинный анализ в информатике, эпидемиологии, ^[20] и социальные науки. ^[21]

Конструкция и терминология

Причинно-следственный график можно построить следующим образом. Каждая переменная в модели имеет соответствующую вершину или узел, и стрелка рисуется от переменной X к переменной Y всякий раз, когда считается, что Y реагирует на изменения X , когда все остальные переменные остаются постоянными. Переменные, связанные с Y прямыми стрелками, называются родительскими для Y или «прямыми причинами Y » и обозначаются Pa(Y) .

Причинно-следственные модели часто включают «члены ошибок» или «пропущенные факторы», которые представляют все неизмеренные факторы, влияющие на переменную Y , когда Pa(Y) остается постоянным. В большинстве случаев члены ошибок исключаются из графика. Однако если автор графика подозревает, что члены ошибок каких-либо двух переменных являются зависимыми (например, две переменные имеют ненаблюдаемую или скрытую общую причину), то между ними рисуется двунаправленная дуга. Таким образом, наличие скрытых переменных учитывается посредством корреляций, которые они вызывают между членами ошибок, что представлено двунаправленными дугами.

Основные инструменты

Фундаментальным инструментом графического анализа является d-разделение , которое позволяет исследователям путем проверки определить, подразумевает ли причинная структура, что два набора переменных независимы с учетом третьего набора. В рекурсивных моделях без коррелированных членов ошибок (иногда называемых марковскими ) эти условные независимости представляют все проверяемые последствия модели. ^[22]

Пример

Предположим, мы хотим оценить влияние посещения элитного колледжа на будущие доходы. Простое регрессирование доходов на рейтинг колледжа не даст объективной оценки целевого эффекта, поскольку элитные колледжи очень избирательны, и студенты, посещающие их, скорее всего, до поступления в школу будут иметь квалификацию для высокооплачиваемой работы. Предполагая, что причинно-следственные связи линейны, эти базовые знания могут быть выражены в следующей спецификации модели структурных уравнений (SEM).

Модель 1

{\begin{aligned}Q_{1}&=U_{1}\\C&=a\cdot Q_{1}+U_{2}\\Q_{2}&=c\cdot C+d\cdot Q_{1}+U_{3}\\S&=b\cdot C+e\cdot Q_{2}+U_{4},\end{aligned}}

где $Q_{1}$ представляет квалификацию человека до поступления в колледж, $Q_{2}$ представляет квалификацию после колледжа, $C$ содержит атрибуты, отражающие качество посещаемого колледжа, и $S$ заработная плата человека.

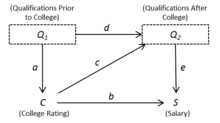
На рисунке 1 показан причинно-следственный график, представляющий данную спецификацию модели. Каждой переменной в модели соответствует соответствующий узел или вершина на графике. Кроме того, для каждого уравнения нарисованы стрелки от независимых переменных к зависимым переменным. Эти стрелки отражают направление причинно-следственной связи. В некоторых случаях мы можем пометить стрелку соответствующим структурным коэффициентом, как показано на рисунке 1.

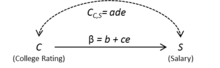
Если $Q_{1}$ и не удалось проанализировать (SVG (MathML можно включить через плагин браузера): неверный ответ («Расширение Math не может подключиться к Restbase.») с сервера «http://localhost:6011/en.wikipedia.org/v1/»: ): {\displaystyle Q_2} являются ненаблюдаемыми или скрытыми переменными, их влияние на $C$ и $S$ можно объяснить их ошибочными условиями. Удалив их, получим следующую спецификацию модели:

Модель 2

{\begin{aligned}C&=U_{C}\\S&=\beta C+U_{S}\end{aligned}}

Справочная информация, указанная в модели 1, подразумевает, что член ошибки $S$ , $U_{S}$ , коррелирует с C ошибкой , $U_{C}$ . В результате мы добавляем двунаправленную дугу между S и C , как на рисунке 2.

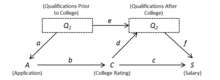
Рисунок 3: Идентифицированная модель со скрытыми переменными ( $Q_{1}$ и $Q_{2}$ ) показано явно

Рисунок 4: Идентифицированная модель с обобщенными скрытыми переменными

С $U_{S}$ коррелирует с $U_{C}$ и, следовательно, $C$ , $C$ является эндогенным и $\beta$ не указан в Модели 2. Однако, если мы учтем убедительность заявления человека в колледж, $A$ , как показано на рисунке 3, мы получаем следующую модель:

Модель 3

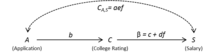
{\begin{aligned}Q_{1}&=U_{1}\\A&=a\cdot Q_{1}+U_{2}\\C&=b\cdot A+U_{3}\\Q_{2}&=e\cdot Q_{1}+d\cdot C+U_{4}\\S&=c\cdot C+f\cdot Q_{2}+U_{5},\end{aligned}}

Удалив скрытые переменные из спецификации модели, мы получим:

Модель 4

{\begin{aligned}A&=a\cdot Q_{1}+U_{A}\\C&=b\cdot A+U_{C}\\S&=\beta \cdot C+U_{S},\end{aligned}}

с $U_{A}$ коррелирует с $U_{S}$ .

Сейчас, $\beta$ идентифицируется и может быть оценен с помощью регрессии $S$ на $C$ и $A$ . Это можно проверить с помощью критерия одной двери : ^[1]^[23] необходимое и достаточное графическое условие для идентификации структурных коэффициентов, таких как $\beta$ , используя регрессию.

Ссылки

^ Jump up to: ^а ^б ^с Перл, Иудея (2000). Причинность . Кембридж, Массачусетс: MIT Press. ISBN 9780521773621 .
^ Тиан, Джин; Перл, Иудея (2002). «Общее условие идентификации причинных последствий» . Материалы восемнадцатой национальной конференции по искусственному интеллекту . ISBN 978-0-262-51129-2 .
^ Шпицер, Илья; Перл, Иудея (2008). «Полные методы идентификации причинной иерархии» (PDF) . Журнал исследований машинного обучения . 9 : 1941–1979.
^ Хуанг, Ю.; Валторта, М. (2006). https://www.aaai.org/Papers/AAAI/2006/AAAI06-180.pdf . {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь ) ; Отсутствует или пусто |title= ( помощь )
^ Барейнбойм, Элиас; Перл, Иудея (2012). «Причинный вывод с помощью суррогатных экспериментов: z-идентифицируемость». Материалы двадцать восьмой конференции по неопределенности в искусственном интеллекте . arXiv : 1210.4842 . Бибкод : 2012arXiv1210.4842B . ISBN 978-0-9749039-8-9 .
^ Тиан, Джин; Перл, Иудея (2002). «О проверяемых последствиях причинных моделей со скрытыми переменными». Материалы восемнадцатой конференции по неопределенности в искусственном интеллекте . стр. 519–27. arXiv : 1301.0608 . Бибкод : 2013arXiv1301.0608T . ISBN 978-1-55860-897-9 .
^ Шпицер, Илья; Перл, Иудея (2008). {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь ) ; Отсутствует или пусто |title= ( помощь )
^ Чен, Брайант; Перл, Иудея (2014). «Проверяемые последствия моделей линейного структурного уравнения» . Материалы конференции AAAI по искусственному интеллекту . 28 . дои : 10.1609/aaai.v28i1.9065 . S2CID 1612893 .
^ Барейнмбойм, Элиас; Перл, Иудея (2014). «Внешняя валидность: от математического расчета к транспортабельности среди населения». Статистическая наука . 29 (4): 579–595. arXiv : 1503.01603 . дои : 10.1214/14-стс486 . S2CID 5586184 .
^ Мохан, Картика; Перл, Иудея; Тиан, Джин (2013). «Графические модели для вывода с отсутствующими данными» (PDF) . Достижения в области нейронных систем обработки информации .
^ Барейнбойм, Элиас; Тиан, Джин; Перл, Иудея (2014). «Восстановление после систематической ошибки выбора в причинно-следственных и статистических выводах» . Материалы конференции AAAI по искусственному интеллекту . 28 . дои : 10.1609/aaai.v28i1.9074 .
^ Райт, С. (1921). «Корреляция и причинно-следственная связь». Журнал сельскохозяйственных исследований . 20 : 557–585.
^ Блэлок, HM (1960). «Корреляционный анализ и причинно-следственные выводы» . Американский антрополог . 62 (4): 624–631. дои : 10.1525/aa.1960.62.4.02a00060 .
^ Дункан, ОД (1966). «Путь анализа: социологические примеры». Американский журнал социологии . 72 : 1–16. дои : 10.1086/224256 . S2CID 59428866 .
^ Дункан, ОД (1976). «Введение в модели структурных уравнений». Американский журнал социологии . 82 (3): 731–733. дои : 10.1086/226377 .
^ Йорескуг, КГ (1969). «Общий подход к подтверждающему факторному анализу максимального правдоподобия». Психометрика . 34 (2): 183–202. дои : 10.1007/bf02289343 . S2CID 186236320 .
^ Гольдбергер, А.С.; Дункан, ОД (1973). Модели структурных уравнений в социальных науках . Нью-Йорк: Семинар Пресс.
^ Гольдбергер, А.С. (1972). «Модели структурных уравнений в социальных науках». Эконометрика . 40 (6): 979–1001. дои : 10.2307/1913851 . JSTOR 1913851 .
^ Уайт, Халберт; Чалак, Карим; Лу, Сюнь (2011). «Связывание причинности Грейнджера и причинной модели Жемчуга с настраиваемыми системами» (PDF) . Причинность во временных рядах. Проблемы машинного обучения . 5 .
^ Ротман, Кеннет Дж.; Гренландия, Сандер; Лэш, Тимоти (2008). Современная эпидемиология . Липпинкотт Уильямс и Уилкинс.
^ Морган, СЛ; Уиншип, К. (2007). Контрафакты и причинно-следственные выводы: методы и принципы социальных исследований . Нью-Йорк: Издательство Кембриджского университета.
^ Гейгер, Дэн; Перл, Иудея (1993). «Логико-алгоритмические свойства условной независимости». Анналы статистики . 21 (4): 2001–2021. CiteSeerX 10.1.1.295.2043 . дои : 10.1214/aos/1176349407 .
^ Чен, Б.; Перл, Дж (2014). «Графические инструменты для моделирования линейными структурными уравнениями» (PDF) . Технический отчет .

[causality-1] Jump up to: ^а ^б ^с Перл, Иудея (2000). Причинность . Кембридж, Массачусетс: MIT Press. ISBN 9780521773621 .

[2] Тиан, Джин; Перл, Иудея (2002). «Общее условие идентификации причинных последствий» . Материалы восемнадцатой национальной конференции по искусственному интеллекту . ISBN 978-0-262-51129-2 .

[3] Шпицер, Илья; Перл, Иудея (2008). «Полные методы идентификации причинной иерархии» (PDF) . Журнал исследований машинного обучения . 9 : 1941–1979.

[4] Хуанг, Ю.; Валторта, М. (2006). https://www.aaai.org/Papers/AAAI/2006/AAAI06-180.pdf . {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь ) ; Отсутствует или пусто |title= ( помощь )

[5] Барейнбойм, Элиас; Перл, Иудея (2012). «Причинный вывод с помощью суррогатных экспериментов: z-идентифицируемость». Материалы двадцать восьмой конференции по неопределенности в искусственном интеллекте . arXiv : 1210.4842 . Бибкод : 2012arXiv1210.4842B . ISBN 978-0-9749039-8-9 .

[6] Тиан, Джин; Перл, Иудея (2002). «О проверяемых последствиях причинных моделей со скрытыми переменными». Материалы восемнадцатой конференции по неопределенности в искусственном интеллекте . стр. 519–27. arXiv : 1301.0608 . Бибкод : 2013arXiv1301.0608T . ISBN 978-1-55860-897-9 .

[7] Шпицер, Илья; Перл, Иудея (2008). {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь ) ; Отсутствует или пусто |title= ( помощь )

[8] Чен, Брайант; Перл, Иудея (2014). «Проверяемые последствия моделей линейного структурного уравнения» . Материалы конференции AAAI по искусственному интеллекту . 28 . дои : 10.1609/aaai.v28i1.9065 . S2CID 1612893 .

[9] Барейнмбойм, Элиас; Перл, Иудея (2014). «Внешняя валидность: от математического расчета к транспортабельности среди населения». Статистическая наука . 29 (4): 579–595. arXiv : 1503.01603 . дои : 10.1214/14-стс486 . S2CID 5586184 .

[10] Мохан, Картика; Перл, Иудея; Тиан, Джин (2013). «Графические модели для вывода с отсутствующими данными» (PDF) . Достижения в области нейронных систем обработки информации .

[11] Барейнбойм, Элиас; Тиан, Джин; Перл, Иудея (2014). «Восстановление после систематической ошибки выбора в причинно-следственных и статистических выводах» . Материалы конференции AAAI по искусственному интеллекту . 28 . дои : 10.1609/aaai.v28i1.9074 .

[12] Райт, С. (1921). «Корреляция и причинно-следственная связь». Журнал сельскохозяйственных исследований . 20 : 557–585.

[13] Блэлок, HM (1960). «Корреляционный анализ и причинно-следственные выводы» . Американский антрополог . 62 (4): 624–631. дои : 10.1525/aa.1960.62.4.02a00060 .

[14] Дункан, ОД (1966). «Путь анализа: социологические примеры». Американский журнал социологии . 72 : 1–16. дои : 10.1086/224256 . S2CID 59428866 .

[15] Дункан, ОД (1976). «Введение в модели структурных уравнений». Американский журнал социологии . 82 (3): 731–733. дои : 10.1086/226377 .

[16] Йорескуг, КГ (1969). «Общий подход к подтверждающему факторному анализу максимального правдоподобия». Психометрика . 34 (2): 183–202. дои : 10.1007/bf02289343 . S2CID 186236320 .

[17] Гольдбергер, А.С.; Дункан, ОД (1973). Модели структурных уравнений в социальных науках . Нью-Йорк: Семинар Пресс.

[18] Гольдбергер, А.С. (1972). «Модели структурных уравнений в социальных науках». Эконометрика . 40 (6): 979–1001. дои : 10.2307/1913851 . JSTOR 1913851 .

[19] Уайт, Халберт; Чалак, Карим; Лу, Сюнь (2011). «Связывание причинности Грейнджера и причинной модели Жемчуга с настраиваемыми системами» (PDF) . Причинность во временных рядах. Проблемы машинного обучения . 5 .

[20] Ротман, Кеннет Дж.; Гренландия, Сандер; Лэш, Тимоти (2008). Современная эпидемиология . Липпинкотт Уильямс и Уилкинс.

[21] Морган, СЛ; Уиншип, К. (2007). Контрафакты и причинно-следственные выводы: методы и принципы социальных исследований . Нью-Йорк: Издательство Кембриджского университета.

[22] Гейгер, Дэн; Перл, Иудея (1993). «Логико-алгоритмические свойства условной независимости». Анналы статистики . 21 (4): 2001–2021. CiteSeerX 10.1.1.295.2043 . дои : 10.1214/aos/1176349407 .

[23] Чен, Б.; Перл, Дж (2014). «Графические инструменты для моделирования линейными структурными уравнениями» (PDF) . Технический отчет .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]