Конструкция Томпсона

В информатике Томпсона построения Томпсона алгоритм , также называемый алгоритмом Макнотона-Ямады- , ^{[ 1 ]} — это метод преобразования регулярного выражения в эквивалентный недетерминированный конечный автомат (НКА). ^{[ 2 ]} Этот NFA можно использовать для сопоставления строк с регулярным выражением. Авторство этого алгоритма принадлежит Кену Томпсону .

Регулярные выражения и недетерминированные конечные автоматы являются двумя представлениями формальных языков . Например, утилиты обработки текста используют регулярные выражения для описания шаблонов расширенного поиска, но NFA лучше подходят для выполнения на компьютере. Следовательно, этот алгоритм представляет практический интерес, поскольку он может компилировать регулярные выражения в NFA. С теоретической точки зрения этот алгоритм является частью доказательства того, что они оба принимают одни и те же языки, то есть обычные языки .

NFA можно сделать детерминированным с помощью конструкции набора степеней , а затем минимизировать , чтобы получить оптимальный автомат, соответствующий данному регулярному выражению. Однако NFA также можно интерпретировать напрямую .

Чтобы решить, описывают ли два заданных регулярных выражения один и тот же язык, каждое из них можно преобразовать в эквивалентный минимальный детерминированный конечный автомат с помощью конструкции Томпсона, конструкции степенного набора и минимизации DFA . Если и только если результирующие автоматы согласны на переименование состояний, языки регулярных выражений соглашаются.

Алгоритм

Алгоритм работает рекурсивно , разбивая выражение на составляющие его подвыражения, из которых будет построен NFA с использованием набора правил. ^{[ 3 ]} Точнее, из регулярного выражения $E$ получен автомат $A$ с функцией перехода $∆$ ^{[ нужны разъяснения ]} учитывает следующие свойства:

$A$ имеет ровно одно начальное состояние $q0,$ которое недоступно из любого другого состояния. То есть для любого состояния $q$ и любой $a$ буквы $\Delta (q,a)$ не содержит $q 0$ .
$A$ имеет ровно одно конечное состояние $qf .$ , которое недоступно из любого другого состояния То есть для любой $а$ буквы $\Delta (q_{f},a)=\emptyset$ .
Пусть $c$ — количество конкатенаций регулярного выражения $E$ , а $s$ — количество символов, не считая круглых скобок, то есть $|$ , $*$ , $а$ и $ε$ . Тогда число состояний $A$ равно $2 s - c$ (линейно по размеру $E$ ).
Число переходов, выходящих из любого состояния, не более двух.
Поскольку NFA $m$ состояний и не более $e$ переходов из каждого состояния может сопоставлять строку длины $n$ за время $O (emn)$ , NFA Томпсона может выполнять сопоставление с образцом за линейное время, предполагая алфавит фиксированного размера. ^{[ 4 ]}^{[ нужен лучший источник ]}

Правила

Следующие правила описаны в соответствии с Aho et al. (2007), ^{[ 1 ]} п. 122. Далее N ( s ) и N ( t ) являются NFA подвыражений песок т соответственно.

Пустое выражение ε преобразуется в

Символ a входного алфавита преобразуется в

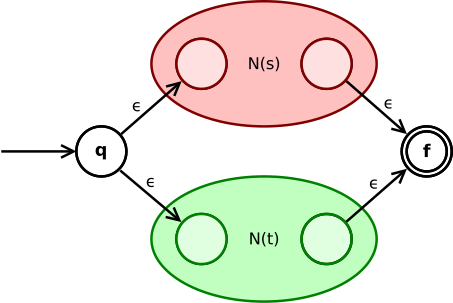
союза Выражение s | t преобразуется в

Состояние q переходит через ε либо в исходное состояние N ( s ) или N ( т ). Их конечные состояния становятся промежуточными состояниями всей НКА и сливаются посредством двух ε-переходов в конечное состояние НКА.

Выражение конкатенации st преобразуется в

Начальное состояние N ( s ) — начальное состояние всей НКА. Конечное состояние N ( s ) становится начальным состоянием N ( т ). Конечное состояние N ( t ) — конечное состояние всего NFA.

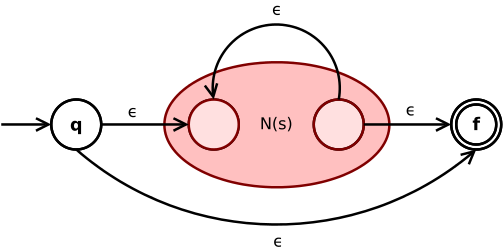
Выражение Клини звезды с ^* преобразуется в

ε-переход соединяет начальное и конечное состояние NFA с суб-NFA N ( с ) между ними. Еще один ε-переход из внутреннего финала во внутреннее начальное состояние N ( s ) допускает повторение выражения По словам звездного оператора.

Выражение в скобках ( s ) преобразуется в N ( с ) сам.

С помощью этих правил, используя правила пустых выражений и символов в качестве базовых случаев, можно с помощью структурной индукции доказать , что любое регулярное выражение можно преобразовать в эквивалентный NFA. ^{[ 1 ]}

Пример

Сейчас будут даны два примера: небольшой неформальный с результатом и более крупный с пошаговым применением алгоритма.

Небольшой пример

Пример `(ε|a*b)` используя конструкцию Томпсона, шаг за шагом

На рисунке ниже показан результат построения Томпсона на (ε|a*b). Фиолетовый овал соответствует a , бирюзовый овал соответствует a* , зеленый овал соответствует b , оранжевый овал соответствует a*b , а синий овал соответствует ε .

Применение алгоритма

В качестве примера на картинке показан результат алгоритма построения Томпсона по регулярному выражению (0|(1(01*(00)*0)*1)*)* который обозначает набор двоичных чисел, кратных 3:

{ ε, "0", "00", "11", "000", "011", "110", "0000", "0011", "0110", "1001", "1100", "1111" , «00000», ... }.

В верхней правой части показана логическая структура (синтаксическое дерево) выражения с знаком "." обозначающий конкатенацию (предполагается, что она имеет переменную арность); подвыражения называются а - q для справочных целей. В левой части показан недетерминированный конечный автомат, полученный в результате алгоритма Томпсона, с вход и состояние выхода каждого подвыражения, окрашенного в цвет пурпурный и голубой соответственно. Метка перехода ε в качестве метки перехода опущена для ясности — немаркированные переходы на самом деле являются переходами ε. Состояние входа и выхода, соответствующее корневому выражению q — стартовое и приемное состояние автомата соответственно.

Шаги алгоритма следующие:

вопрос :	начните конвертировать выражение звезды Клини									`(0\|(1(01(00)0)1))*`
	б :	начать конвертировать выражение объединения								`0\|(1(01(00)0)1)`
		а :	конвертировать символ							`0`
		п :	начните конвертировать выражение звезды Клини							`(1(01(00)0)1)`
			д :	начать преобразование выражения конкатенации						`1(01(00)0)*1`
				с :	конвертировать символ					`1`
				н :	начните конвертировать выражение звезды Клини					`(01(00)0)*`
					ж :	начать преобразование выражения конкатенации				`01(00)0`
						и :	конвертировать символ			`0`
						ч :	начните конвертировать выражение звезды Клини			`1*`
							г :	конвертировать символ		`1`
						ч :	закончил преобразование выражения звезды Клини			`1*`
						л :	начните конвертировать выражение звезды Клини			`(00)*`
							Дж :	начать преобразование выражения конкатенации		`00`
								я :	конвертировать символ	`0`
								к :	конвертировать символ	`0`
							Дж :	завершено преобразование выражения конкатенации		`00`
						л :	закончил преобразование выражения звезды Клини			`(00)*`
						м :	конвертировать символ			`0`
					ж :	завершено преобразование выражения конкатенации				`01(00)0`
				н :	закончил преобразование выражения звезды Клини					`(01(00)0)*`
				о :	конвертировать символ					`1`
			д :	завершено преобразование выражения конкатенации						`1(01(00)0)*1`
		п :	закончил преобразование выражения звезды Клини							`(1(01(00)0)1)`
	б :	завершено преобразование выражения объединения								`0\|(1(01(00)0)1)`
вопрос :	закончил преобразование выражения звезды Клини									`(0\|(1(01(00)0)1))*`

Эквивалентный минимальный детерминированный автомат показан ниже.

Связь с другими алгоритмами

Томпсона — один из нескольких алгоритмов построения NFA из регулярных выражений; ^{[ 5 ]} более ранний алгоритм был предложен Макнотоном и Ямадой. ^{[ 6 ]} В отличие от конструкции Томпсона, алгоритм Клини преобразует конечный автомат в регулярное выражение.

Алгоритм построения Глушкова аналогичен конструкции Томпсона, если исключить ε-переходы.

Ссылки

^ Jump up to: ^а ^б ^с Альфред Вайно Ахо ; Моника С. Лам ; Рави Сетхи ; Джеффри Д. Уллман (2007). «3.7.4 Построение NFA из регулярного выражения» (печать) . Составители: принципы, методы и инструменты (2-е изд.). Бостон, Массачусетс, США: Пирсон Аддисон-Уэсли. п. 159–163 . ISBN 9780321486813 .
^ Лауден, Кеннет К. (1997). «2.4.1 От регулярного выражения к NFA» (печать) . Конструкция компилятора: Принципы и практика (3-е изд.). 20 Park Plaza Boston, MA 02116-4324, США: Издательская компания PWS. стр. 64–69. ISBN 978-0-534-93972-4 . {{cite book}}: CS1 maint: местоположение ( ссылка )
^ Кен Томпсон (июнь 1968 г.). «Техника программирования: Алгоритм поиска по регулярным выражениям» . Коммуникации АКМ . 11 (6): 419–422. дои : 10.1145/363347.363387 . S2CID 21260384 .
^ Син, Гуанмин. «Минимизированный Томпсон NFA» (PDF) .
^ Уотсон, Брюс В. (1995). Таксономия алгоритмов построения конечных автоматов (PDF) (Технический отчет). Эйндховенский технологический университет . Отчет по информатике 93/43.
^ Р. Макнотон, Х. Ямада (март 1960 г.). «Регулярные выражения и графы состояний для автоматов». Транзакции IEEE на электронных компьютерах . 9 (1): 39–47. дои : 10.1109/TEC.1960.5221603 .

[DragonBook-1] Jump up to: ^а ^б ^с Альфред Вайно Ахо ; Моника С. Лам ; Рави Сетхи ; Джеффри Д. Уллман (2007). «3.7.4 Построение NFA из регулярного выражения» (печать) . Составители: принципы, методы и инструменты (2-е изд.). Бостон, Массачусетс, США: Пирсон Аддисон-Уэсли. п. 159–163 . ISBN 9780321486813 .

[2] Лауден, Кеннет К. (1997). «2.4.1 От регулярного выражения к NFA» (печать) . Конструкция компилятора: Принципы и практика (3-е изд.). 20 Park Plaza Boston, MA 02116-4324, США: Издательская компания PWS. стр. 64–69. ISBN 978-0-534-93972-4 . {{cite book}}: CS1 maint: местоположение ( ссылка )

[3] Кен Томпсон (июнь 1968 г.). «Техника программирования: Алгоритм поиска по регулярным выражениям» . Коммуникации АКМ . 11 (6): 419–422. дои : 10.1145/363347.363387 . S2CID 21260384 .

[4] Син, Гуанмин. «Минимизированный Томпсон NFA» (PDF) .

[5] Уотсон, Брюс В. (1995). Таксономия алгоритмов построения конечных автоматов (PDF) (Технический отчет). Эйндховенский технологический университет . Отчет по информатике 93/43.

[6] Р. Макнотон, Х. Ямада (март 1960 г.). «Регулярные выражения и графы состояний для автоматов». Транзакции IEEE на электронных компьютерах . 9 (1): 39–47. дои : 10.1109/TEC.1960.5221603 .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

v т и Струны
String metric	Approximate string matching Bitap algorithm Damerau–Levenshtein distance Edit distance Gestalt pattern matching Hamming distance Jaro–Winkler distance Lee distance Levenshtein automaton Levenshtein distance Wagner–Fischer algorithm
String-searching algorithm	Apostolico–Giancarlo algorithm Boyer–Moore string-search algorithm Boyer–Moore–Horspool algorithm Knuth–Morris–Pratt algorithm Rabin–Karp algorithm Raita algorithm Trigram search Two-way string-matching algorithm Zhu–Takaoka string matching algorithm
Multiple string searching	Aho–Corasick Commentz-Walter algorithm
Regular expression	Comparison of regular-expression engines Regular grammar Thompson's construction Nondeterministic finite automaton
Sequence alignment	BLAST Hirschberg's algorithm Needleman–Wunsch algorithm Smith–Waterman algorithm
Data structure	DAFSA Suffix array Suffix automaton Suffix tree Generalized suffix tree Rope Ternary search tree Trie
Other	Parsing Pattern matching Compressed pattern matching Longest common subsequence Longest common substring Sequential pattern mining Sorting String rewriting systems String operations