Расстояние Хэмминга

Расстояние Хэмминга
4-битный двоичный тессеракт для определения расстояния Хэмминга.	Два примера расстояний: 0100→1001 имеет расстояние 3; 0110→1110 имеет расстояние 1
Сорт	Сходство строк
Структура данных	нить
Худшая производительность
Лучшая производительность
Средняя производительность
Наихудшая пространственная сложность

3-битный двоичный куб для определения расстояния Хэмминга

Два примера расстояний: 100→011 имеет расстояние 3; 010→111 имеет расстояние 2

Минимальное расстояние между любыми двумя вершинами — это расстояние Хэмминга между двумя двоичными строками.

В теории информации между расстояние Хэмминга двумя строками или векторами одинаковой длины — это количество позиций, в которых соответствующие символы различны. Другими словами, он измеряет минимальное количество замен, необходимых для замены одной строки на другую, или, что то же самое, минимальное количество ошибок , которые могли бы преобразовать одну строку в другую. В более общем контексте расстояние Хэмминга — это одна из нескольких строковых метрик для измерения расстояния редактирования между двумя последовательностями. Оно названо в честь американского математика Ричарда Хэмминга .

Основное применение — в теории кодирования , точнее, в блочных кодах , в которых строки одинаковой длины являются векторами над конечным полем .

Определение [ править ]

Расстояние Хэмминга между двумя строками символов одинаковой длины — это количество позиций, в которых соответствующие символы различны. ^[1]

Примеры [ править ]

Символами могут быть буквы, биты или десятичные цифры, а также другие возможности. Например, расстояние Хэмминга между:

« ka roll in » и « ka thr in » — это 3.
« ка р ол ин » и « к е р ст ин » — 3.
« К атр в » и « керст в » — это 4.
0000 и 1111 — это 4.
2 17 3 8 96 и 2 23 3 7 96 равно 3.

Свойства [ править ]

Для фиксированной длины n расстояние Хэмминга является метрикой на множестве слов длины n (также известном как пространство Хэмминга ), поскольку оно удовлетворяет условиям неотрицательности, симметрии, расстояние Хэмминга двух слов равно 0. удовлетворяет неравенству треугольника : тогда и только тогда, когда два слова идентичны и также ^[2] Действительно, если мы зафиксируем три слова a , b и c , то всякий раз, когда есть разница между i -й буквой a и i -й буквой c , то должна быть разница и между i -й буквой a и i- й буквой. буква b или между i -й буквой b и i- й буквой c . Следовательно, расстояние Хэмминга между a и c не больше суммы расстояний Хэмминга между a и b и между b и c . Расстояние Хэмминга между двумя словами a и b также можно рассматривать как вес Хэмминга a - b для соответствующего выбора оператора -, так же, как разницу между двумя целыми числами можно рассматривать как расстояние от нуля на числовой прямой. ^{[ нужны разъяснения ]}

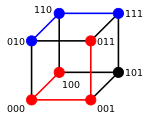
Для двоичных строк a и b расстояние Хэмминга равно количеству единиц ( населения ) в XOR b количество . ^[3] Метрическое пространство двоичных строк длиной n с расстоянием Хэмминга известно как куб Хэмминга ; как метрическое пространство оно эквивалентно множеству расстояний между вершинами графа гиперкуба . Можно также рассматривать двоичную строку длины n как вектор в $\mathbb {R} ^{n}$ рассматривая каждый символ в строке как действительную координату; при таком вложении строки образуют вершины n- мерного гиперкуба , а расстояние Хэмминга строк эквивалентно манхэттенскому расстоянию между вершинами.

Обнаружение и исправление ошибок [ править ]

Минимальное расстояние Хэмминга или минимальное расстояние (обычно обозначаемое d _min ) используется для определения некоторых важных понятий в теории кодирования , таких как коды обнаружения и исправления ошибок . В частности, код C считается обнаруживающим k ошибок тогда и только тогда, когда минимальное расстояние Хэмминга между любыми двумя его кодовыми словами составляет не менее k +1. ^[2]

Например, рассмотрим код, состоящий из двух кодовых слов «000» и «111». Расстояние Хэмминга между этими двумя словами равно 3, и, следовательно, обнаружение ошибок k =2. Это означает, что если инвертировать один бит или инвертировать два бита, ошибка может быть обнаружена. Если три бита перевернуты, то «000» становится «111», и ошибка не может быть обнаружена.

Код C называется исправляющим k-ошибки , если для каждого слова w в базовом пространстве Хэмминга H существует не более одного кодового слова c (из C ) такого, что расстояние Хэмминга между w и c не превышает k . Другими словами, код исправляет k -ошибок, если минимальное расстояние Хэмминга между любыми двумя его кодовыми словами составляет не менее 2k +1 . Геометрически это также понимается как любые замкнутые шары радиуса k с центрами на различных кодовых словах. непересекающиеся ^[2] также называются сферами Хэмминга . Эти шары в этом контексте ^[4]

Например, рассмотрим один и тот же 3-битный код, состоящий из двух кодовых слов «000» и «111». Пространство Хэмминга состоит из 8 слов 000, 001, 010, 011, 100, 101, 110 и 111. Кодовое слово «000» и слова с однобитовой ошибкой «001», «010», «100» меньше или равно расстоянию Хэмминга от 1 до «000». Аналогично, кодовое слово «111» и его слова с однобитовой ошибкой «110», «101» и «011» находятся в пределах 1 расстояния Хэмминга от исходного «111». В этом коде ошибка в один бит всегда находится в пределах 1 расстояния Хэмминга от исходных кодов, и код может быть исправлен с 1 ошибкой , то есть k=1 . Поскольку расстояние Хэмминга между «000» и «111» равно 3, а они включают весь набор кодовых слов в коде, минимальное расстояние Хэмминга равно 3, что удовлетворяет 2k+1 = 3 .

Таким образом, код с минимальным расстоянием Хэмминга d между своими кодовыми словами может обнаружить не более d -1 ошибок и исправить ошибки ⌊( d -1)/2⌋. ^[2] Последнее число также называют радиусом упаковки или исправлять ошибки . способностью кода ^[4]

История и приложения [ править ]

Расстояние Хэмминга названо в честь Ричарда Хэмминга , который представил эту концепцию в своей фундаментальной статье о Хэмминга кодах «Коды обнаружения и исправления ошибок » в 1950 году. ^[5] Весовой анализ битов по Хэммингу используется в нескольких дисциплинах, включая теорию информации , теорию кодирования и криптографию . ^[6]

Он используется в телекоммуникациях для подсчета количества перевернутых битов в двоичном слове фиксированной длины в качестве оценки ошибки, и поэтому иногда его называют сигнальным расстоянием . ^[7] Для q -арных строк в алфавите размера q ≥ 2 расстояние Хэмминга применяется в случае q-ичного симметричного канала , тогда как расстояние Ли используется для фазовой манипуляции или, в более общем плане, каналов, подверженных ошибкам синхронизации , поскольку расстояние учитывает ошибки ±1. ^[8] Если $q=2$ или $q=3$ оба расстояния совпадают, поскольку любая пара элементов из ${\textstyle \mathbb {Z} /2\mathbb {Z} }$ или ${\textstyle \mathbb {Z} /3\mathbb {Z} }$ отличаются на 1, но расстояния различны для больших $q$ .

Расстояние Хэмминга также используется в систематике как мера генетической дистанции. ^[9]

Однако для сравнения строк разной длины или строк, в которых следует ожидать не только замен, но и вставок или удалений, более сложная метрика, такая как расстояние Левенштейна более подходит .

Пример алгоритма [ править ]

Следующая функция, написанная на Python 3, возвращает расстояние Хэмминга между двумя строками:

def hamming_distance(string1: str, string2: str) -> int:
    """Return the Hamming distance between two strings."""
    if len(string1) != len(string2):
        raise ValueError("Strings must be of equal length.")
    dist_counter = 0
    for n in range(len(string1)):
        if string1[n] != string2[n]:
            dist_counter += 1
    return dist_counter

Или, в более коротком выражении:

sum(char1 != char2 for char1, char2 in zip(string1, string2, strict=True))

Функция hamming_distance(), реализованный в Python 3 , вычисляет расстояние Хэмминга между двумя строками (или другими повторяемыми объектами) одинаковой длины, создавая последовательность логических значений, указывающих несоответствия и совпадения между соответствующими позициями на двух входных данных, а затем суммируя последовательность со значениями True и False. , интерпретируемые как единица и ноль соответственно.

def hamming_distance(s1: str, s2: str) -> int:
    """Return the Hamming distance between equal-length sequences."""
    if len(s1) != len(s2):
        raise ValueError("Undefined for sequences of unequal length.")
    return sum(char1 != char2 for char1, char2 in zip(s1, s2))

где функция zip() объединяет две коллекции одинаковой длины в пары.

Следующая функция C вычисляет расстояние Хэмминга двух целых чисел (рассматриваемых как двоичные значения, то есть как последовательности битов). Время выполнения этой процедуры пропорционально расстоянию Хэмминга, а не количеству бит во входных данных. Он вычисляет побитовое исключающее ИЛИ из двух входных данных, а затем находит вес Хэмминга результата (количество ненулевых битов), используя алгоритм Вегнера (1960) , который неоднократно находит и очищает ненулевой бит младшего порядка. Некоторые компиляторы поддерживают функцию __builtin_popcount , которая может вычислить это, используя специализированное процессорное оборудование, если оно доступно.

int hamming_distance(unsigned x, unsigned y)
{
    int dist = 0;

    // The ^ operators sets to 1 only the bits that are different
    for (unsigned val = x ^ y; val > 0; ++dist)
    {
        // We then count the bit set to 1 using the Peter Wegner way
        val = val & (val - 1); // Set to zero val's lowest-order 1
    }

    // Return the number of differing bits
    return dist;
}

Более быстрая альтернатива — использовать ассемблерную инструкцию подсчета населения ( popcount ). Некоторые компиляторы, такие как GCC и Clang, делают его доступным через встроенную функцию:

// Hamming distance for 32-bit integers
int hamming_distance32(unsigned int x, unsigned int y)
{
    return __builtin_popcount(x ^ y);
}

// Hamming distance for 64-bit integers
int hamming_distance64(unsigned long long x, unsigned long long y)
{
    return __builtin_popcountll(x ^ y);
}

См. также [ править ]

Ссылки [ править ]

^ Ваггенер, Билл (1995). Методы импульсно-кодовой модуляции . Спрингер. п. 206. ИСБН 978-0-442-01436-0 . Проверено 13 июня 2020 г.
↑ Перейти обратно: Перейти обратно: ^а ^б ^с ^д Робинсон, Дерек Дж.С. (2003). Введение в абстрактную алгебру . Вальтер де Грюйтер . стр. 255–257. ISBN 978-3-11-019816-4 .
^ Уоррен-младший, Генри С. (2013) [2002]. Хакерское наслаждение (2-е изд.). Аддисон Уэсли – Pearson Education, Inc., стр. 81–96. ISBN 978-0-321-84268-8 . 0-321-84268-5.
↑ Перейти обратно: Перейти обратно: ^а ^б Коэн, Г .; Хонкала, И.; Лицын С.; Лобштейн, А. (1997), Покрывающие коды , Математическая библиотека Северной Голландии, том. 54, Elsevier , стр. 16–17, ISBN. 978-0-08-053007-9
^ Хэмминг, RW (апрель 1950 г.). «Коды обнаружения и исправления ошибок» (PDF) . Технический журнал Bell System . 29 (2): 147–160. дои : 10.1002/j.1538-7305.1950.tb00463.x . hdl : 10945/46756 . ISSN 0005-8580 . S2CID 61141773 . Архивировано (PDF) из оригинала 9 октября 2022 г.
^ Джаррус, Айман; Пинкас, Бенни (2009). «Безопасные вычисления на основе расстояния Хэмминга и их приложения». В Абдалле, Мишель; Пойнтчеваль, Дэвид; Фуке, Пьер-Ален; Верно, Дэмиен (ред.). Прикладная криптография и сетевая безопасность . Конспекты лекций по информатике. Том. 5536. Берлин, Гейдельберг: Springer. стр. 107–124. дои : 10.1007/978-3-642-01957-9_7 . ISBN 978-3-642-01957-9 .
^ Аяла, Хосе (2012). Проектирование интегральных схем и систем . Спрингер . п. 62. ИСБН 978-3-642-36156-2 .
^ Рот, Рон (2006). Введение в теорию кодирования . Издательство Кембриджского университета . п. 298. ИСБН 978-0-521-84504-5 .
^ Пилчер, Кристофер Д.; Вонг, Джозеф К.; Пиллаи, Сатиш К. (18 марта 2008 г.). «Вывод о динамике передачи ВИЧ на основе взаимоотношений филогенетических последовательностей» . ПЛОС Медицина . 5 (3): е69. doi : 10.1371/journal.pmed.0050069 . ISSN 1549-1676 . ПМК 2267810 . ПМИД 18351799 .

Дальнейшее чтение [ править ]

В этой статье использованы общедоступные материалы из Федеральный стандарт 1037C . Управление общего обслуживания . Архивировано из оригинала 22 января 2022 г.
Вегнер, Питер (1960). «Техника счета единиц в двоичном компьютере» . Коммуникации АКМ . 3 (5): 322. дои : 10.1145/367236.367286 . S2CID 31683715 .
Маккей, Дэвид Дж. К. (2003). Теория информации, вывод и алгоритмы обучения . Кембридж: Издательство Кембриджского университета . ISBN 0-521-64298-1 .

[1] Ваггенер, Билл (1995). Методы импульсно-кодовой модуляции . Спрингер. п. 206. ИСБН 978-0-442-01436-0 . Проверено 13 июня 2020 г.

[Robinson2003-2] Перейти обратно: Перейти обратно: ^а ^б ^с ^д Робинсон, Дерек Дж.С. (2003). Введение в абстрактную алгебру . Вальтер де Грюйтер . стр. 255–257. ISBN 978-3-11-019816-4 .

[Warren_2013-3] Уоррен-младший, Генри С. (2013) [2002]. Хакерское наслаждение (2-е изд.). Аддисон Уэсли – Pearson Education, Inc., стр. 81–96. ISBN 978-0-321-84268-8 . 0-321-84268-5.

[cc17-4] Перейти обратно: Перейти обратно: ^а ^б Коэн, Г .; Хонкала, И.; Лицын С.; Лобштейн, А. (1997), Покрывающие коды , Математическая библиотека Северной Голландии, том. 54, Elsevier , стр. 16–17, ISBN. 978-0-08-053007-9

[5] Хэмминг, RW (апрель 1950 г.). «Коды обнаружения и исправления ошибок» (PDF) . Технический журнал Bell System . 29 (2): 147–160. дои : 10.1002/j.1538-7305.1950.tb00463.x . hdl : 10945/46756 . ISSN 0005-8580 . S2CID 61141773 . Архивировано (PDF) из оригинала 9 октября 2022 г.

[6] Джаррус, Айман; Пинкас, Бенни (2009). «Безопасные вычисления на основе расстояния Хэмминга и их приложения». В Абдалле, Мишель; Пойнтчеваль, Дэвид; Фуке, Пьер-Ален; Верно, Дэмиен (ред.). Прикладная криптография и сетевая безопасность . Конспекты лекций по информатике. Том. 5536. Берлин, Гейдельберг: Springer. стр. 107–124. дои : 10.1007/978-3-642-01957-9_7 . ISBN 978-3-642-01957-9 .

[Ayala2012-7] Аяла, Хосе (2012). Проектирование интегральных схем и систем . Спрингер . п. 62. ИСБН 978-3-642-36156-2 .

[Roth2006-8] Рот, Рон (2006). Введение в теорию кодирования . Издательство Кембриджского университета . п. 298. ИСБН 978-0-521-84504-5 .

[9] Пилчер, Кристофер Д.; Вонг, Джозеф К.; Пиллаи, Сатиш К. (18 марта 2008 г.). «Вывод о динамике передачи ВИЧ на основе взаимоотношений филогенетических последовательностей» . ПЛОС Медицина . 5 (3): е69. doi : 10.1371/journal.pmed.0050069 . ISSN 1549-1676 . ПМК 2267810 . ПМИД 18351799 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

v т и Струны
Строковая метрика	Примерное соответствие строк Алгоритм битап Расстояние Дамерау – Левенштейна Изменить расстояние Сопоставление гештальт-образцов Расстояние Хэмминга Расстояние Яро – Винклера Расстояние Ли Автомат Левенштейна Расстояние Левенштейна Алгоритм Вагнера-Фишера
Алгоритм поиска строк	Алгоритм Апостола – Джанкарло Алгоритм поиска строк Бойера – Мура Алгоритм Бойера – Мура – Хорспула Алгоритм Кнута – Морриса – Пратта Алгоритм Рабина – Карпа Алгоритм Райта Триграммный поиск Алгоритм двустороннего сопоставления строк Алгоритм сопоставления строк Чжу – Такаока
Поиск нескольких строк	Ахо – Корасик Алгоритм Комментца-Вальтера
Регулярное выражение	Сравнение механизмов регулярных выражений Регулярная грамматика Конструкция Томпсона Недетерминированный конечный автомат
Выравнивание последовательности	ВЗРЫВ Алгоритм Хиршберга Алгоритм Нидлмана – Вунша Алгоритм Смита – Уотермана
Структура данных	ДАФСА Суффиксный массив Суффиксный автомат Суффиксное дерево Обобщенное суффиксное дерево Веревка Тернарное дерево поиска Три
Другой	Разбор Сопоставление с образцом Сопоставление сжатого шаблона Самая длинная общая подпоследовательность Самая длинная общая подстрока Последовательный анализ шаблонов Сортировка Системы перезаписи строк Строковые операции