Неравенство треугольника

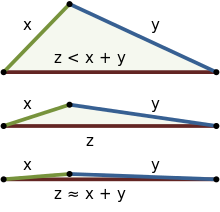
Три примера неравенства треугольника для треугольников со сторонами длиной $x$ , $y$ , $z$ . В верхнем примере показан случай, когда $z$ намного меньше суммы $x + y$ двух других сторон, а в нижнем примере показан случай, когда сторона $z$ лишь немного меньше $x + y$ .

В математике неравенство треугольника гласит, что для любого треугольника сумма длин любых двух сторон должна быть больше или равна длине оставшейся стороны. ^[1]^[2] Это утверждение допускает включение вырожденных треугольников , но некоторые авторы, особенно пишущие об элементарной геометрии, исключают эту возможность, тем самым упуская из виду возможность равенства. ^[3] Если $x$ , $y$ и $z$ — длины сторон треугольника, причем ни одна из сторон не превышает $z$ , то неравенство треугольника утверждает, что

z\leq x+y,

с равенством только в вырожденном случае треугольника нулевой площади.

В евклидовой геометрии и некоторых других геометриях неравенство треугольника представляет собой теорему о расстояниях и записывается с использованием векторов и длин векторов ( норм ):

\|\mathbf {x} +\mathbf {y} \|\leq \|\mathbf {x} \|+\|\mathbf {y} \|,

где длина $z$ третьей стороны заменена векторной суммой $x + y$ . Когда $x$ и $y$ — действительные числа , их можно рассматривать как векторы в $\mathbb {R} ^{1}$ , а неравенство треугольника выражает связь между абсолютными значениями .

В евклидовой геометрии для прямоугольных треугольников неравенство треугольника является следствием теоремы Пифагора , а для общих треугольников — следствием закона косинусов , хотя его можно доказать и без этих теорем. Неравенство можно рассматривать интуитивно либо в $\mathbb {R} ^{2}$ или $\mathbb {R} ^{3}$ . На рисунке справа показаны три примера, начиная с явного неравенства (вверху) и приближаясь к равенству (внизу). В евклидовом случае равенство возникает только в том случае, если треугольник имеет $угол 180°$ и два $угла 0°$ , что делает три вершины коллинеарными , как показано в нижнем примере. Таким образом, в евклидовой геометрии кратчайшим расстоянием между двумя точками является прямая линия.

В сферической геометрии кратчайшее расстояние между двумя точками — это дуга большого круга , но неравенство треугольника сохраняется при условии, что сделано ограничение, согласно которому расстояние между двумя точками на сфере равно длине меньшего сферического отрезка линии (т. е. один с центральным углом в $[0, π]$ ) с этими конечными точками. ^[4]^[5]

Неравенство треугольника является определяющим свойством и норм мер расстояния . Это свойство должно быть установлено в виде теоремы для любой функции, предложенной для таких целей для каждого конкретного пространства: например, таких пространств, как действительные числа , евклидовы пространства , L ^п пространства ( $p \geq 1$ ) и пространства внутреннего произведения .

Евклидова геометрия [ править ]

Евклид доказал неравенство треугольника для расстояний в плоской геометрии, используя конструкцию, изображенную на рисунке. ^[6]Начиная с треугольника $ABC$ , строится равнобедренный треугольник, одна сторона которого принимается за $BC$ , а другая равна катету $BD$ вдоль продолжения стороны $AB$ . Затем утверждается, что угол $β$ имеет большую величину, чем угол $α$ , поэтому сторона $AD$ длиннее стороны $AC$ . Однако:

{\overline {AD}}={\overline {AB}}+{\overline {BD}}={\overline {AB}}+{\overline {BC}},

следовательно, сумма длин сторон $AB$ и $BC$ больше длины $AC$ . Это доказательство появляется в «Началах» Евклида , книга 1, предложение 20. ^[7]

Математическое выражение ограничения на сторонах треугольника [ править ]

Для правильного треугольника неравенство треугольника, как оно сформулировано словами, буквально переводится в три неравенства (учитывая, что правильный треугольник имеет длины сторон $a, b, c$ , которые все положительны, и исключает вырожденный случай нулевой площади):

a+b>c,\quad b+c>a,\quad c+a>b.

Можно показать, что более сжатая форма этой системы неравенства:

|a-b|<c<a+b.

Другой способ заявить об этом:

\max(a,b,c)<a+b+c-\max(a,b,c)

подразумевая

2\max(a,b,c)<a+b+c

и, таким образом, длина самой длинной стороны меньше полупериметра .

Математически эквивалентная формулировка состоит в том, что площадь треугольника со сторонами $a, b, c$ должна быть действительным числом, большим нуля. Формула Герона для площади:

{\begin{aligned}4\cdot {\text{area}}&={\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}\\&={\sqrt {-a^{4}-b^{4}-c^{4}+2a^{2}b^{2}+2a^{2}c^{2}+2b^{2}c^{2}}}.\end{aligned}}

С точки зрения любого выражения площади неравенство треугольника, наложенное на все стороны, эквивалентно условию, что выражение под знаком квадратного корня действительно и больше нуля (поэтому выражение площади действительно и больше нуля).

Неравенство треугольника обеспечивает еще два интересных ограничения для треугольников, стороны которых равны $a, b, c$ , где $a \geq b \geq c$ и $\phi$ это золотое сечение , так как

1<{\frac {a+c}{b}}<3

1\leq \min \left({\frac {a}{b}},{\frac {b}{c}}\right)<\phi .

^[8]

Прямоугольный треугольник [ править ]

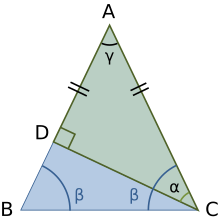
В случае прямоугольных треугольников неравенство треугольника сводится к утверждению, что гипотенуза больше любой из двух сторон и меньше их суммы. ^[9]

Вторая часть этой теоремы уже установлена выше для любой стороны любого треугольника. Первая часть устанавливается с помощью нижнего рисунка. На рисунке рассмотрим прямоугольный треугольник $ADC$ . Равнобедренный треугольник $ABC$ построен с равными сторонами $AB = AC$ . Согласно постулату треугольника , углы в прямоугольном треугольнике $ADC$ удовлетворяют:

\alpha +\gamma =\pi /2\ .

Аналогично, в равнобедренном треугольнике $ABC$ углы удовлетворяют:

2\beta +\gamma =\pi \ .

Поэтому,

\alpha =\pi /2-\gamma ,\ \mathrm {while} \ \beta =\pi /2-\gamma /2\ ,

и поэтому, в частности,

\alpha <\beta \ .

Это означает, что сторона $AD$ , противоположная углу $α$ , короче стороны $AB$ , противоположной большему углу $β$ . Но $АВ = АС$ . Следовательно:

{\overline {AC}}>{\overline {AD}}\ .

Аналогичная конструкция показывает $AC > DC$ , что доказывает теорему.

Альтернативное доказательство (также основанное на постулате треугольника) основано на рассмотрении трех положений точки $B$ : ^[10] (i) как изображено (что необходимо доказать), или (ii) $B$ совпадает с $D$ (что означало бы, что равнобедренный треугольник имел два прямых угла в качестве основных углов плюс угол при вершине $γ$ , что нарушило бы постулат треугольника ), или наконец, (iii) $B$ внутри прямоугольного треугольника между точками $A$ и $D$ (в этом случае угол $ABC$ является внешним углом прямоугольного треугольника $BDC$ и, следовательно, больше $π /2$ , что означает, что другой основной угол равнобедренного треугольника также равен больше $π /2$ и их сумма превышает $π$ в нарушение постулата треугольника).

Эта теорема, устанавливающая неравенства, уточнена теоремой Пифагора до равенства, что квадрат длины гипотенузы равен сумме квадратов двух других сторон.

Примеры использования [ править ]

Рассмотрим треугольник, стороны которого находятся в арифметической прогрессии , и пусть стороны равны $a, a + d, a + 2 d$ . Тогда неравенство треугольника требует, чтобы

{\begin{array}{rcccl}0&<&a&<&2a+3d,\\0&<&a+d&<&2a+2d,\\0&<&a+2d&<&2a+d.\end{array}}

Для удовлетворения всех этих неравенств требуется

a>0{\text{ and }}-{\frac {a}{3}}<d<a.

^[11]

Когда $d$ выбирается так, что $d = a /3$ , получается прямоугольный треугольник, который всегда подобен тройке Пифагора со сторонами $3$ , $4$ , $5$ .

Теперь рассмотрим треугольник, стороны которого находятся в геометрической прогрессии , и пусть стороны равны $a, ar, ar. 2$ . Тогда неравенство треугольника требует, чтобы

{\begin{array}{rcccl}0&<&a&<&ar+ar^{2},\\0&<&ar&<&a+ar^{2},\\0&<&\!ar^{2}&<&a+ar.\end{array}}

Первое неравенство требует $a > 0$ ; следовательно, его можно разделить и устранить. При $a > 0$ среднее неравенство требует только $r > 0$ . Теперь первое и третье неравенства должны удовлетворять

{\begin{aligned}r^{2}+r-1&{}>0\\r^{2}-r-1&{}<0.\end{aligned}}

Первое из этих квадратных неравенств требует, $чтобы r$ находился в области, превышающей значение положительного корня квадратного уравнения $r. 2 + r - 1 = 0$ , т. е. $r > φ - 1$ , где $φ$ — золотое сечение . Второе квадратное неравенство требует, $чтобы r$ находился в диапазоне от 0 до положительного корня квадратного уравнения $r. 2 - р - 1 знак равно 0$ , т. е. $0 < р < φ$ . Объединенные требования приводят к тому, что $r$ ограничивается диапазоном

\varphi -1<r<\varphi \,{\text{ and }}a>0.

^[12]

Когда $r$ общее отношение выбирается так, что $r = \sqrt φ,$ оно образует прямоугольный треугольник, который всегда подобен треугольнику Кеплера .

Обобщение на любой полигон [ править ]

Неравенство треугольника можно путем математической индукции распространить на произвольные ломаные пути, показав, что общая длина такого пути не меньше длины прямой между его концами. Следовательно, длина любой стороны многоугольника всегда меньше суммы длин других сторон многоугольника.

Пример обобщенного неравенства многоугольника для четырехугольника [ править ]

Рассмотрим четырехугольник, стороны которого находятся в геометрической прогрессии , и пусть стороны равны $a, ar, ar 2, С 3$ . Тогда обобщенное неравенство многоугольника требует, чтобы

{\begin{array}{rcccl}0&<&a&<&ar+ar^{2}+ar^{3}\\0&<&ar&<&a+ar^{2}+ar^{3}\\0&<&ar^{2}&<&a+ar+ar^{3}\\0&<&ar^{3}&<&a+ar+ar^{2}.\end{array}}

Эти неравенства при $a > 0$ сводятся к следующему

r^{3}+r^{2}+r-1>0

r^{3}-r^{2}-r-1<0.

^[13]

Левые части полиномов этих двух неравенств имеют корни, которые являются константой Трибоначчи и обратной ей величиной. Следовательно, $r$ ограничен диапазоном $1/ t < r < t$ , где $t$ — константа Трибоначчи.

Связь с кратчайшими путями [ править ]

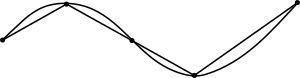
Длина дуги кривой определяется как наименьшая верхняя граница длин полигональных аппроксимаций.

Это обобщение можно использовать, чтобы доказать, что кратчайшая кривая между двумя точками в евклидовой геометрии представляет собой прямую линию.

Ни один многоугольный путь между двумя точками не короче линии между ними. Это означает, что ни одна кривая не может иметь длину дуги меньше расстояния между ее конечными точками. По определению, длина дуги кривой — это наименьшая верхняя граница длин всех полигональных аппроксимаций кривой. Результат для полигональных путей показывает, что прямая линия между конечными точками является самой короткой из всех полигональных аппроксимаций. Поскольку длина дуги кривой больше или равна длине каждой полигональной аппроксимации, сама кривая не может быть короче прямой линии. ^[14]

Конверс [ править ]

Верно и обратное утверждение теоремы о неравенстве треугольника: если три действительных числа таковы, что каждое из них меньше суммы других, то существует треугольник, длины сторон которого являются этими числами, и с положительной площадью; и если одно число равно сумме двух других, существует вырожденный треугольник (то есть с нулевой площадью) с этими числами в качестве длин сторон.

В любом случае, если длины сторон равны $a$ , $b$ , $c,$ мы можем попытаться разместить треугольник в евклидовой плоскости , как показано на схеме. Нам нужно доказать, что существует действительное число $h,$ соответствующее значениям $a$ , $b$ и $c$ , и в этом случае этот треугольник существует.

По теореме Пифагора имеем $b 2 = час 2 + д 2$ и $ 2 = час 2 + (с - d) 2$ согласно рисунку справа. Вычитание этих значений $дает 2 - б 2 = с 2 - 2 компакт-диска$ . Это уравнение позволяет нам выразить $d$ через стороны треугольника:

d={\frac {-a^{2}+b^{2}+c^{2}}{2c}}.

Для высоты треугольника имеем $h 2 = б 2 - д 2$ . Заменив $d$ формулой, приведенной выше, получим

h^{2}=b^{2}-\left({\frac {-a^{2}+b^{2}+c^{2}}{2c}}\right)^{2}.

Чтобы действительное число $h$ удовлетворяло этому требованию, $h 2$ должно быть неотрицательным:

{\begin{aligned}0&\leq b^{2}-\left({\frac {-a^{2}+b^{2}+c^{2}}{2c}}\right)^{2}\\[4pt]0&\leq \left(b-{\frac {-a^{2}+b^{2}+c^{2}}{2c}}\right)\left(b+{\frac {-a^{2}+b^{2}+c^{2}}{2c}}\right)\\[4pt]0&\leq \left(a^{2}-(b-c)^{2})((b+c)^{2}-a^{2}\right)\\[6pt]0&\leq (a+b-c)(a-b+c)(b+c+a)(b+c-a)\\[6pt]0&\leq (a+b-c)(a+c-b)(b+c-a)\end{aligned}}

что справедливо, если неравенство треугольника выполняется для всех сторон. Следовательно, существует действительное число $h$ в соответствии со сторонами $a,b,c$ , и треугольник существует. Если каждое неравенство треугольника выполняется строго , $h>0$ и треугольник невырожден (имеет положительную площадь); но если одно из неравенств выполняется с равенством, то $h=0$ , треугольник вырожден.

Обобщение на более высокие измерения [ править ]

Площадь треугольной грани тетраэдра меньше или равна сумме площадей трех других треугольных граней. В более общем смысле, в евклидовом пространстве гиперобъем $(n - 1)$ - симплекса меньше $- грани n$ или равен сумме гиперобъемов других $n$ граней.

Подобно тому, как неравенство треугольника обобщается на неравенство многоугольника, неравенство для симплекса любой размерности обобщается на многогранник любой размерности: гиперобъем любой грани многогранника меньше или равен сумме гиперобъемов остальных граней. .

В некоторых случаях тетраэдрическое неравенство сильнее некоторых применений неравенства треугольника. Например, неравенство треугольника, по-видимому, допускает возможность существования четырех точек $A$ , $B$ , $C$ и $Z$ в евклидовом пространстве, таких что расстояния

АВ = ВС = СА = 26

и

AZ = BZ = CZ = 14

.

Однако точек с такими расстояниями существовать не может: площадь равностороннего треугольника $ABC$ 26–26–26 равна $169 \sqrt 3$ , что в три раза больше $39 \sqrt 3$ , площади равнобедренного треугольника 26–14–14 (все по формула Герона ), поэтому расположение запрещено тетраэдрическим неравенством.

Нормированное векторное пространство [ править ]

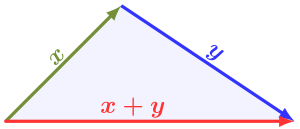
Неравенство треугольника для норм векторов.

В нормированном векторном пространстве $V$ одним из определяющих свойств нормы является неравенство треугольника:

\|x+y\|\leq \|x\|+\|y\|\quad \forall \,x,y\in V

то есть норма суммы двух векторов не превышает суммы норм двух векторов. Это также называется субаддитивностью . Чтобы любая предложенная функция вела себя как норма, она должна удовлетворять этому требованию. ^[15]

Если нормированное пространство евклидово или, шире, строго выпуклое , то $\|x+y\|=\|x\|+\|y\|$ тогда и только тогда, когда треугольник, образованный $x$ , $y$ и $x + y$ , вырожден, то есть $x$ и $y$ находятся на одном луче, т. е. $x = 0$ или $y = 0$ , или $x = α y$ для некоторого $α > 0$ . Это свойство характеризует строго выпуклые нормированные пространства, такие как $пространства ℓ p$ с $1 < p < \infty$ . Однако существуют нормированные пространства, в которых это неверно. Например, рассмотрим плоскость с $нормой ℓ 1$ ( манхэттенское расстояние ) и обозначим $x = (1, 0)$ и $y = (0, 1)$ . Тогда треугольник, образованный $x$ , $y$ и $x + y$ , невырожден, но

\|x+y\|=\|(1,1)\|=|1|+|1|=2=\|x\|+\|y\|.

Примеры норм [ править ]

Абсолютное значение как норма для реальной линии . Чтобы быть нормой, неравенство треугольника требует, чтобы абсолютное значение удовлетворяло любым действительным числам $x$ и $y$ : $|x+y|\leq |x|+|y|,$ что он и делает.

Доказательство: ^[16]

-\left\vert x\right\vert \leq x\leq \left\vert x\right\vert

-\left\vert y\right\vert \leq y\leq \left\vert y\right\vert

После добавления,

-(\left\vert x\right\vert +\left\vert y\right\vert )\leq x+y\leq \left\vert x\right\vert +\left\vert y\right\vert

Используйте тот факт, что $\left\vert b\right\vert \leq a\Leftrightarrow -a\leq b\leq a$ (с $заменой b$ на $x + y$ и $a$ на $\left\vert x\right\vert +\left\vert y\right\vert$ ), у нас есть

|x+y|\leq |x|+|y|

Неравенство треугольника полезно в математическом анализе для определения наилучшей верхней оценки размера суммы двух чисел с точки зрения размеров отдельных чисел.

Существует также нижняя оценка, которую можно найти с помощью неравенства обратного треугольника , которое гласит, что для любых действительных чисел $x$ и $y$ :

|x-y|\geq {\biggl |}|x|-|y|{\biggr |}.

Внутренний продукт как норма в пространстве внутреннего продукта . Если норма возникает из скалярного произведения (как в случае евклидовых пространств), то неравенство треугольника следует из неравенства Коши – Шварца следующим образом: заданные векторы $x$ и $y$ и обозначая внутренний продукт как $\langle x,y\rangle$ : ^[17]

$\\|x+y\\|^{2}$	$=\langle x+y,x+y\rangle$
	$=\\|x\\|^{2}+\langle x,y\rangle +\langle y,x\rangle +\\|y\\|^{2}$
	$\leq \\|x\\|^{2}+2\|\langle x,y\rangle \|+\\|y\\|^{2}$
	$\leq \\|x\\|^{2}+2\\|x\\|\\|y\\|+\\|y\\|^{2}$ (по неравенству Коши–Шварца)
	$=\left(\\|x\\|+\\|y\\|\right)^{2}$ .

Неравенство Коши–Шварца превращается в равенство тогда и только тогда, когда $x$ и $y$ линейно зависимы. Неравенство $\langle x,y\rangle +\langle y,x\rangle \leq 2\left|\left\langle x,y\right\rangle \right|$ превращается в равенство для линейно зависимых $x$ и $y$ тогда и только тогда, когда один из векторов $x$ или $y$ является неотрицательным скаляром другого.

Извлечение квадратного корня из конечного результата дает неравенство треугольника.

$p$ -норма : обычно используемой нормой является $p$ -норма: $\|x\|_{p}=\left(\sum _{i=1}^{n}|x_{i}|^{p}\right)^{1/p}\ ,$ где $x i$ — компоненты вектора $x$ . При $p = 2$ p $-$ норма становится евклидовой нормой : $\|x\|_{2}=\left(\sum _{i=1}^{n}|x_{i}|^{2}\right)^{1/2}=\left(\sum _{i=1}^{n}x_{i}^{2}\right)^{1/2}\ ,$ это теорема Пифагора в $n$ -мерностях, особый случай, соответствующий норме скалярного произведения. За исключением случая $p = 2$ , $p$ является -норма не нормой скалярного произведения, поскольку она не удовлетворяет закону параллелограмма . Неравенство треугольника для общих значений $p$ называется неравенством Минковского . ^[18] Он принимает форму: $\|x+y\|_{p}\leq \|x\|_{p}+\|y\|_{p}\ .$

Метрическое пространство [ править ]

В метрическом пространстве $M$ с метрикой $d$ неравенство треугольника является требованием к расстоянию :

d(x,\ z)\leq d(x,\ y)+d(y,\ z)\ ,

для $x$ , $y$ , $z$ в $M.$ всех То есть расстояние от $x$ до $z$ не превышает суммы расстояния от $x$ до $y$ и расстояния от $y$ до $z$ .

Неравенство треугольника отвечает за большую часть интересной структуры метрического пространства, а именно за сходимость. Это связано с тем, что остальные требования к метрике по сравнению с ними довольно упрощены. Например, тот факт, что любая сходящаяся последовательность в метрическом пространстве является последовательностью Коши , является прямым следствием неравенства треугольника, поскольку если мы выберем любые $x n$ и $x m$ такие, что $d (x n, x) < ε /2$ и $d (x m, x) < ε /2$ , где $ε > 0$ задано и произвольно (как в определении предела в метрическом пространстве), то по неравенству треугольника $d (x n, x m) \leq d (x n, x) + d (x m, x) < ε /2 + ε /2 = ε$ , так что последовательность ${x n}$ является последовательностью Коши по определению.

Эта версия неравенства треугольника сводится к указанной выше в случае нормированных векторных пространств, где метрика индуцируется через $d (x, y) ≔ ‖ x - y ‖$ , где $x - y$ является вектором, указывающим из точки $y$ в $x.$ .

Неравенство обратного треугольника [ править ]

Неравенство обратного треугольника — это логически эквивалентная альтернативная формулировка неравенства треугольника, которая дает нижние границы вместо верхних. Для плоской геометрии утверждение следующее: ^[19]

Любая сторона треугольника больше или равна разности двух других сторон .

В случае нормированного векторного пространства утверждение выглядит следующим образом:

{\bigg |}\|x\|-\|y\|{\bigg |}\leq \|x-y\|,

или для метрических пространств, $|d(x,z)-d(y,z)|\leq d(x,y)$ . Это означает, что норма $\|\cdot \|$ а также расстояние от- $z$ функция $d(z,\cdot )$ непрерывны по Липшицу с константой Липшица $1$ и поэтому, в частности, равномерно непрерывны .

Для доказательства обратного неравенства треугольника от обычного используется $\|y-x\|=\|{-}1(x-y)\|=|{-}1|\cdot \|x-y\|=\|x-y\|$ найти:

\|x\|=\|(x-y)+y\|\leq \|x-y\|+\|y\|\Rightarrow \|x\|-\|y\|\leq \|x-y\|,

\|y\|=\|(y-x)+x\|\leq \|y-x\|+\|x\|\Rightarrow \|x\|-\|y\|\geq -\|x-y\|,

Объединение этих двух утверждений дает:

-\|x-y\|\leq \|x\|-\|y\|\leq \|x-y\|\Rightarrow {\bigg |}\|x\|-\|y\|{\bigg |}\leq \|x-y\|.

Обратно, доказательство неравенства треугольника из обратного неравенства треугольника работает в двух случаях:

Если $\|x+y\|-\|x\|\geq 0,$ тогда по обратному неравенству треугольника $\|x+y\|-\|x\|={\bigg |}\|x+y\|-\|x\|{\bigg |}\leq \|(x+y)-x\|=\|y\|\Rightarrow \|x+y\|\leq \|x\|+\|y\|$ ,

и если $\|x+y\|-\|x\|<0,$ тогда тривиально $\|x\|+\|y\|\geq \|x\|>\|x+y\|$ по неотрицательности нормы.

Таким образом, в обоих случаях мы получаем, что $\|x\|+\|y\|\geq \|x+y\|$ .

Для метрических пространств доказательство неравенства обратного треугольника находится аналогично:

$d(x,y)+d(y,z)\geq d(x,z)\Rightarrow d(x,y)\geq d(x,z)-d(y,z)$

$d(z,x)+d(x,y)\geq d(z,y)\Rightarrow d(x,y)\geq d(y,z)-d(x,z)$

Сложив эти уравнения вместе, находим:

$d(x,y)\geq |d(x,z)-d(y,z)|$

И в обратном порядке, начиная с обратного неравенства треугольника, мы снова можем использовать два случая:

Если $d(x,z)-d(y,z)\geq 0$ , затем $d(x,y)\geq |d(x,z)-d(y,z)|=d(x,z)-d(y,z)\Rightarrow d(x,y)+d(y,z)\geq d(x,z)$ ,

и если $d(x,z)-d(y,z)<0,$ затем $d(x,y)+d(y,z)\geq d(y,z)>d(x,z)$ снова по неотрицательности метрики.

Таким образом, в обоих случаях мы получаем, что $d(x,y)+d(y,z)\geq d(x,z)$ .

Неравенство треугольника подобия для косинусного

Применяя функцию косинуса к неравенству треугольника и обратному неравенству треугольника для длин дуг и используя формулы сложения и вычитания углов для косинусов, сразу же следует, что

\operatorname {sim} (x,z)\geq \operatorname {sim} (x,y)\cdot \operatorname {sim} (y,z)-{\sqrt {\left(1-\operatorname {sim} (x,y)^{2}\right)\cdot \left(1-\operatorname {sim} (y,z)^{2}\right)}}

и

\operatorname {sim} (x,z)\leq \operatorname {sim} (x,y)\cdot \operatorname {sim} (y,z)+{\sqrt {\left(1-\operatorname {sim} (x,y)^{2}\right)\cdot \left(1-\operatorname {sim} (y,z)^{2}\right)}}\,.

С помощью этих формул нужно вычислить квадратный корень для каждой исследуемой тройки векторов ${x, y, z}$ , а не $arccos(sim(x, y))$ для каждой исследуемой пары векторов ${x, y}$ , и может быть улучшение производительности, если количество проверенных троек меньше количества проверенных пар.

Обращение в пространстве Минковского [ править ]

Минковского пространства Метрика $\eta _{\mu \nu }$ не является положительно определенным, что означает, что $\|x\|^{2}=\eta _{\mu \nu }x^{\mu }x^{\nu }$ может иметь либо знак, либо нуль, даже если вектор $x$ не равен нулю. Более того, если $x$ и $y$ являются времениподобными векторами, лежащими в световом конусе будущего, неравенство треугольника меняется на противоположное:

\|x+y\|\geq \|x\|+\|y\|.

Физическим примером этого неравенства является парадокс близнецов в специальной теории относительности . Та же обратная форма неравенства справедлива, если оба вектора лежат в световом конусе прошлого и если один или оба являются нулевыми векторами. Результат сохраняется в $n+1$ размеры для любых $n\geq 1$ . Если плоскость, определяемая $x$ и $y$ подобно пространству (и, следовательно, является евклидовым подпространством), то выполняется обычное неравенство треугольника.

См. также [ править ]

Примечания [ править ]

^ Wolfram MathWorld – http://mathworld.wolfram.com/TriangleInequality.html
^ Мохамед А. Хамси; Уильям А. Кирк (2001). «§1.4 Неравенство треугольника в $R н$ " . Введение в метрические пространства и теорию неподвижной точки . Wiley-IEEE. ISBN 0-471-41825-0 .
^ например, Джейкобс, Гарольд Р. (1974), Геометрия , WH Freeman & Co., с. 246, ISBN 0-7167-0456-0
^ Оливер Брок; Джефф Тринкль; Фабио Рамос (2009). Робототехника: наука и системы IV . МТИ Пресс. п. 195. ИСБН 978-0-262-51309-8 .
^ Арлан Рамзи; Роберт Д. Рихтмайер (1995). Введение в гиперболическую геометрию . Спрингер. п. 17 . ISBN 0-387-94339-0 .
^ Гарольд Р. Джейкобс (2003). Геометрия: видеть, делать, понимать (3-е изд.). Макмиллан. п. 201. ИСБН 0-7167-4361-2 .
^ Дэвид Э. Джойс (1997). «Элементы Евклида, Книга 1, Предложение 20» . Элементы Евклида . Кафедра математики и информатики, Университет Кларка . Проверено 25 июня 2010 г.
↑ American Mathematical Monthly , стр. 49–50, 1954.
^ Клод Ирвин Палмер (1919). Практическая математика для домашнего обучения: основы арифметики, геометрии, алгебры и тригонометрии . МакГроу-Хилл. п. 422 .
^ Александр Завайра; Гэвин Хичкок (2009). «Лемма 1: В прямоугольном треугольнике гипотенуза больше любой из двух других сторон» . Букварь для соревнований по математике . Издательство Оксфордского университета. ISBN 978-0-19-953988-8 .
^ Вольфрам|Альфа. "вход: решить 0<a<2a+3d, 0<a+d<2a+2d, 0<a+2d<2a+d, " . Вольфрам Исследования . Проверено 7 сентября 2010 г.
^ Вольфрам|Альфа. "вход: решить 0<a<ar+ar ², 0<ar<a+ar ², 0<ар ²<a+ar » . Wolfram Research . Проверено 7 сентября 2010 г.
^ Вольфрам|Альфа. "вход: решить 0<a<ar+ar ²+ с ³, 0<ар ³<а+ар+ар ²" . Wolfram Research . Проверено 29 июля 2012 г.
^ Джон Стиллвелл (1997). Числа и геометрия . Спрингер. ISBN 978-0-387-98289-2 . п. 95.
^ Райнер Кресс (1988). «§3.1: Нормированные пространства» . Численный анализ . Спрингер. п. 26. ISBN 0-387-98408-9 .
^ Джеймс Стюарт (2008). Основное исчисление . Томсон Брукс/Коул. п. А10. ISBN 978-0-495-10860-3 .
^ Джон Стиллвелл (2005). Четыре столпа геометрии . Спрингер. п. 80 . ISBN 0-387-25530-3 .
^ Карен Сакс (2002). Начало функционального анализа . Спрингер. п. 61. ИСБН 0-387-95224-1 .
^ Аноним (1854 г.). «Упражнение I. к предложению XIX» . Популярный педагог; четвертый том . Ладгейт-Хилл, Лондон: Джон Касселл. п. 196.

Ссылки [ править ]

Педо, Дэниел (1988). Геометрия: Комплексный курс . Дувр. ISBN 0-486-65812-0 . .
Рудин, Уолтер (1976). Принципы математического анализа . Нью-Йорк: МакГроу-Хилл . ISBN 0-07-054235-Х . .

Внешние ссылки [ править ]

Неравенство треугольника в ProofWiki

[1] Wolfram MathWorld – http://mathworld.wolfram.com/TriangleInequality.html

[Khamsi-2] Мохамед А. Хамси; Уильям А. Кирк (2001). «§1.4 Неравенство треугольника в $R н$ " . Введение в метрические пространства и теорию неподвижной точки . Wiley-IEEE. ISBN 0-471-41825-0 .

[3] например, Джейкобс, Гарольд Р. (1974), Геометрия , WH Freeman & Co., с. 246, ISBN 0-7167-0456-0

[Ramos-4] Оливер Брок; Джефф Тринкль; Фабио Рамос (2009). Робототехника: наука и системы IV . МТИ Пресс. п. 195. ИСБН 978-0-262-51309-8 .

[Ramsay-5] Арлан Рамзи; Роберт Д. Рихтмайер (1995). Введение в гиперболическую геометрию . Спрингер. п. 17 . ISBN 0-387-94339-0 .

[Jacobs-6] Гарольд Р. Джейкобс (2003). Геометрия: видеть, делать, понимать (3-е изд.). Макмиллан. п. 201. ИСБН 0-7167-4361-2 .

[Joyce-7] Дэвид Э. Джойс (1997). «Элементы Евклида, Книга 1, Предложение 20» . Элементы Евклида . Кафедра математики и информатики, Университет Кларка . Проверено 25 июня 2010 г.

[8] American Mathematical Monthly , стр. 49–50, 1954.

[Palmer-9] Клод Ирвин Палмер (1919). Практическая математика для домашнего обучения: основы арифметики, геометрии, алгебры и тригонометрии . МакГроу-Хилл. п. 422 .

[Zawaira-10] Александр Завайра; Гэвин Хичкок (2009). «Лемма 1: В прямоугольном треугольнике гипотенуза больше любой из двух других сторон» . Букварь для соревнований по математике . Издательство Оксфордского университета. ISBN 978-0-19-953988-8 .

[11] Вольфрам|Альфа. "вход: решить 0<a<2a+3d, 0<a+d<2a+2d, 0<a+2d<2a+d, " . Вольфрам Исследования . Проверено 7 сентября 2010 г.

[12] Вольфрам|Альфа. "вход: решить 0<a<ar+ar ², 0<ar<a+ar ², 0<ар ²<a+ar » . Wolfram Research . Проверено 7 сентября 2010 г.

[13] Вольфрам|Альфа. "вход: решить 0<a<ar+ar ²+ с ³, 0<ар ³<а+ар+ар ²" . Wolfram Research . Проверено 29 июля 2012 г.

[14] Джон Стиллвелл (1997). Числа и геометрия . Спрингер. ISBN 978-0-387-98289-2 . п. 95.

[Kress-15] Райнер Кресс (1988). «§3.1: Нормированные пространства» . Численный анализ . Спрингер. п. 26. ISBN 0-387-98408-9 .

[Stewart-16] Джеймс Стюарт (2008). Основное исчисление . Томсон Брукс/Коул. п. А10. ISBN 978-0-495-10860-3 .

[Stillwell-17] Джон Стиллвелл (2005). Четыре столпа геометрии . Спрингер. п. 80 . ISBN 0-387-25530-3 .

[Saxe-18] Карен Сакс (2002). Начало функционального анализа . Спрингер. п. 61. ИСБН 0-387-95224-1 .

[inequality-19] Аноним (1854 г.). «Упражнение I. к предложению XIX» . Популярный педагог; четвертый том . Ладгейт-Хилл, Лондон: Джон Касселл. п. 196.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

$\\|x+y\\|^{2}$	$=\langle x+y,x+y\rangle$
	$=\\|x\\|^{2}+\langle x,y\rangle +\langle y,x\rangle +\\|y\\|^{2}$
	$\leq \\|x\\|^{2}+2\|\langle x,y\rangle \|+\\|y\\|^{2}$
	$\leq \\|x\\|^{2}+2\\|x\\|\\|y\\|+\\|y\\|^{2}$ (по неравенству Коши–Шварца)
	$=\left(\\|x\\|+\\|y\\|\right)^{2}$ .