Треугольник Кеплера

Это хорошая статья. Нажмите здесь для получения дополнительной информации.

Треугольник Кеплера — прямоугольный треугольник, образованный тремя квадратами, площади которых находятся в геометрической прогрессии согласно золотому сечению .

Треугольник Кеплера — это особый прямоугольный треугольник , длины сторон которого находятся в геометрической прогрессии . Коэффициент прогрессии где это золотое сечение , и прогрессию можно записать: , или приблизительно . Квадраты на краях этого треугольника имеют площади в другой геометрической прогрессии: . Альтернативные определения того же треугольника характеризуют его с точки зрения трех пифагорейских средних двух чисел или через радиус равнобедренных треугольников .

Этот треугольник назван в честь Иоганна Кеплера , но его можно найти и в более ранних источниках. Хотя некоторые источники утверждают, что древнеегипетские пирамиды имели пропорции, основанные на треугольнике Кеплера, большинство ученых полагают, что золотое сечение не было известно египетской математике и архитектуре.

История [ править ]

Треугольник Кеплера назван в честь немецкого математика и астронома Иоганна Кеплера (1571–1630), который написал об этой форме в письме 1597 года. [1] Две концепции, которые можно использовать для анализа этого треугольника, теорема Пифагора и золотое сечение, представляли интерес для Кеплера, как он писал в другом месте:

У геометрии есть два великих сокровища: одно — теорема Пифагора, другое — деление прямой на экстремальное и среднее отношение. Первое мы можем сравнить с массой золота, второе мы можем назвать драгоценным камнем. [2]

Однако Кеплер был не первым, кто описал этот треугольник. [3] Сам Кеплер приписывал это «профессору музыки по имени Магирус». [1] Тот же треугольник появляется ранее в книге по арабской математике , Liber mensurationum Абу Бекра, известной из перевода XII века Герарда Кремонского на латынь: [3] [4] и в Practica geometriae [ it ] Фибоначчи (опубликовано в 1220–1221 гг . ), Который определил ее аналогично Кеплеру. [3] [5] Немного раньше, чем Кеплер, об этом написал Педро Нуньес в 1567 году, и «вероятно, оно было широко распространено в рукописных традициях позднего средневековья и Возрождения». [3] Его также несколько раз независимо переоткрывали позже, чем Кеплера. [1]

Прямоугольный треугольник, образованный средней точкой ребра, центральной точкой основания и вершиной квадратной пирамиды . Некоторые пирамидологи предполагают, что треугольник, образованный таким образом для Великой пирамиды в Гизе, был задуман как треугольник Кеплера.

По мнению некоторых авторов, «золотая пирамида» с удвоенным треугольником Кеплера в поперечном сечении точно описывает конструкцию египетских пирамид, таких как Великая пирамида в Гизе ; Одним из источников этой теории является неправильное прочтение Геродота в XIX веке пирамидологом Джоном Тейлором. [6] [7] Для той же пирамиды было предложено множество других теорий пропорций, не связанных с треугольником Кеплера. [1] [6] [8] Поскольку эти различные теории очень похожи в получаемых ими числовых значениях, а также из-за неточностей в измерениях, отчасти вызванных разрушением внешней поверхности пирамиды, такие теории трудно разрешить, основываясь исключительно на физических доказательствах. [6] [9] Совпадение пропорций с треугольником Кеплера вполне может быть численным совпадением: по мнению учёных, исследовавших эту взаимосвязь, древние египтяне, скорее всего, не знали о золотом сечении и не использовали его в своей математике и архитектуре. [1] [8] [10] [11] Вместо этого пропорции пирамиды можно адекватно объяснить, используя целочисленные соотношения, основанные на прямоугольном треугольнике со сторонами 11 и 14. [1] [6]

Название «треугольник Кеплера» для этой формы было использовано Роджером Герц-Фишлером на основе письма Кеплера 1597 года еще в 1979 году. [7] Другое название того же треугольника, использованное Матилой Гикой в ​​его книге 1946 года о золотом сечении « Геометрия искусства и жизни », — «треугольник Прайса», в честь пирамидолога У.А. Прайса. [12]

Определения [ править ]

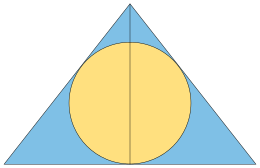
Когда равнобедренный треугольник образуется из двух треугольников Кеплера, отраженных от их длинных сторон, он имеет максимально возможный внутренний радиус среди всех равнобедренных треугольников, имеющих катеты заданного размера.

Треугольник Кеплера однозначно определяется свойствами прямоугольного треугольника и тем, что длины его сторон находятся в геометрической прогрессии:или, что то же самое, иметь квадраты по сторонам в геометрической прогрессии. Отношение прогрессии длин сторон равно , где это золотое сечение , и прогрессию можно записать: , или примерно 1:1,272:1,618. Квадраты на краях этого треугольника имеют площади в другой геометрической прогрессии: .Тот факт, что треугольник с этими пропорциями является прямоугольным, следует из того факта, что для квадратов длин сторон с этими пропорциямиопределяющий полином золотого сечения такой же, как формула, данная теоремой Пифагора для квадратов длин ребер прямоугольного треугольника:

Поскольку это уравнение верно для золотого сечения, эти три длины подчиняются теореме Пифагора и образуют прямоугольный треугольник. И наоборот, в любом прямоугольном треугольнике, квадраты длин сторон которого находятся в геометрической прогрессии с любым соотношением , из теоремы Пифагора следует, что это соотношение подчиняется тождеству . Следовательно, соотношение должно быть единственным положительным решением этого уравнения, золотым сечением, а треугольник должен быть треугольником Кеплера. [1]

Три длины ребра , и являются средним гармоническим , средним геометрическим и средним арифметическим соответственно двух чисел . [13] [14] Все эти три способа объединения двух чисел изучались в древнегреческой математике и называются пифагорейскими средствами . [15] И наоборот, это можно рассматривать как альтернативное определение треугольника Кеплера: это прямоугольный треугольник, длины ребер которого равны трем пифагорейским средним значениям некоторых двух чисел. Единственные треугольники, для которых это верно, — это треугольники Кеплера. [13] [14]

Третий, эквивалентный способ определения этого треугольника исходит из проблемы максимизации радиуса равнобедренного треугольника .Среди всех равнобедренных треугольников с фиксированным выбором длины двух равных сторон, но с переменной длиной основания, треугольник с наибольшим внутренним радиусом формируется из двух копий треугольника Кеплера, отраженных друг от друга через свои длинные стороны. Следовательно, треугольник Кеплера можно определить как прямоугольный треугольник, который среди всех прямоугольных треугольников с одинаковой гипотенузой образует своим отражением равнобедренный треугольник максимального радиуса. [16] То же отражение также образует равнобедренный треугольник, который для данного периметра содержит максимально возможный полукруг . [17]

Свойства [ править ]

В локсодромной последовательности касательных окружностей Коксетера центры каждых трех последовательных окружностей образуют угол, образующий треугольник Кеплера.

Если короткая сторона треугольника Кеплера имеет длину , остальные стороны будут иметь длины и . Площадь можно рассчитать по стандартной формуле площади прямоугольного треугольника (половины произведения двух коротких сторон): . Косинус : большего из двух непрямых углов представляет собой отношение прилежащей стороны (более короткой из двух сторон) к гипотенузе , откуда следует, что два непрямых угла равны [1]

и

Ежи Кочик заметил, что больший из этих двух углов также является углом, образованным центрами троек последовательных окружностей в локсодромной последовательности касательных окружностей Коксетера . [18]

См. также [ править ]

  • Автомедиановый треугольник — треугольник, квадраты длин сторон которого образуют арифметическую прогрессию, включая прямоугольный треугольник с длинами сторон.
  • Золотой треугольник — равнобедренный треугольник, отношение длины основания к длине стороны которого равно золотому сечению.

Ссылки [ править ]

  1. ↑ Перейти обратно: Перейти обратно: а б с д и ж г час Герц-Фишлер, Роджер (2000). Форма Великой пирамиды . Ватерлоо, Онтарио: Издательство Университета Уилфрида Лорье . ISBN  0-88920-324-5 . МР   1788996 . Вся книга рассматривает множество альтернативных теорий формы этой пирамиды. См. главу 11, «Теория треугольника Кеплера», стр. 80–91, для получения материалов, касающихся треугольника Кеплера, и стр. 80–91. 166 за вывод о том, что теория треугольника Кеплера может быть устранена по принципу: «Теория должна соответствовать уровню математики, соответствующему тому, что было известно древним египтянам». См. примечание 3, с. 229, по истории работы Кеплера с этим треугольником.
  2. ^ Финк, Карл (1903). Краткая история математики: авторизованный перевод книги доктора Карла Финка Geschichte der Elementar-Mathematik . Перевод Бемана, Вустера Вудраффа; Смит, Дэвид Юджин (2-е изд.). Чикаго: Издательская компания Open Court . п. 223 .
  3. ↑ Перейти обратно: Перейти обратно: а б с д Хойруп, Йенс (2002). «Обзор формы Великой пирамиды Роджера Герц-Фишлера» (PDF) . Математические обзоры . МР   1788996 . Архивировано (PDF) из оригинала 23 февраля 2022 г. Проверено 23 февраля 2022 г.
  4. ^ Басард, Хьюберт Л.Л. (апрель – июнь 1968 г.). «L'algèbre au Moyen Âge: le «Liber mensurationum» d'Abû Bekr» . Journal des Savants (на французском и латыни). 1968 (2): 65–124. дои : 10.3406/jds.1968.1175 . Архивировано из оригинала 12 января 2022 г. Проверено 12 января 2022 г. См. задачу 51, воспроизведенную на стр. 98
  5. ^ Хьюз, Варнава, изд. (2008). Практика геометрии Фибоначчи . Источники и исследования по истории математики и физических наук. Нью-Йорк: Спрингер. стр. 130–131. дои : 10.1007/978-0-387-72931-2 . ISBN  978-0-387-72930-5 . МР   2364574 .
  6. ↑ Перейти обратно: Перейти обратно: а б с д Бартлетт, Кристофер (май 2014 г.). «Проект Великой пирамиды Хуфу» . Сетевой журнал Nexus . 16 (2): 299–311. дои : 10.1007/s00004-014-0193-9 . S2CID   122021107 .
  7. ↑ Перейти обратно: Перейти обратно: а б Фишлер, Р. (1979). «Что на самом деле сказал Геродот? или как построить (теорию) Великой пирамиды». Окружающая среда и планирование B: Планирование и дизайн . 6 (1): 89–93. дои : 10.1068/b060089 . S2CID   62210630 .
  8. ↑ Перейти обратно: Перейти обратно: а б Росси, Коринна (2004). Архитектура и математика в Древнем Египте . Издательство Кембриджского университета. стр. 67–68. ISBN  978-0-521-82954-0 . ни в одном древнеегипетском письменном математическом источнике нет прямых свидетельств каких-либо арифметических вычислений или геометрических построений, которые можно было бы классифицировать как Золотое сечение... , и само по себе как число не соответствует дошедшим до нас математическим источникам Среднего царства ; см. также обширное обсуждение множества альтернативных теорий формы пирамиды и другой египетской архитектуры, стр. 7–56.
  9. ^ Энглин, WS (1994). «Великая пирамидальная чепуха». Математика: краткая история и философия . Тексты для бакалавриата по математике. Нью-Йорк: Springer-Verlag . п. 4. дои : 10.1007/978-1-4612-0875-4 . ISBN  0-387-94280-7 . МР   1301327 .
  10. ^ Росси, Коринна ; Тут, Кристофер А. (2002). «Были ли в Древнем Египте известны ряды Фибоначчи и Золотое сечение?» . История Математики . 29 (2): 101–113. дои : 10.1006/hmat.2001.2334 . HDL : 11311/997099 . МР   1896969 .
  11. ^ Марковский, Джордж (январь 1992 г.). «Заблуждения о золотом сечении» (PDF) . Математический журнал колледжа . 23 (1). Математическая ассоциация Америки : 2–19. дои : 10.2307/2686193 . JSTOR   2686193 . Архивировано (PDF) из оригинала 11 декабря 2020 г. Проверено 29 июня 2012 г. Похоже, что египтяне вообще не знали о существовании гораздо меньше включали его в свои здания
  12. ^ Гика, Матила Костиеску (1946). Геометрия искусства и жизни . Нью-Йорк: Шид и Уорд . п. 22.
  13. ↑ Перейти обратно: Перейти обратно: а б Брюс, Ян (1994). «Еще один пример золотого прямоугольного треугольника» (PDF) . Ежеквартальный журнал Фибоначчи . 32 (3): 232–233. МР   1285752 . Архивировано (PDF) из оригинала 29 января 2022 г. Проверено 29 января 2022 г.
  14. ↑ Перейти обратно: Перейти обратно: а б Ди Доменико, Анджело (июль 2005 г.). «89.41 Золотое сечение — прямоугольный треугольник — и средние арифметические, геометрические и гармонические». Математический вестник . 89 (515): 261. дои : 10.1017/s0025557200177769 . JSTOR   3621234 . S2CID   123738769 .
  15. ^ Хаффман, Карл (2005). «Архит и история средств» . Архит Тарентский: царь-пифагорейец, философ и математик . Издательство Кембриджского университета . стр. 170–177. ISBN  978-1-139-44407-1 . Архивировано из оригинала 22 января 2022 г. Проверено 22 января 2022 г.
  16. ^ Халлек, Эзра (март 2012 г.). «Обучающий совет: рассмотрите круглую корову». Математический журнал колледжа . 43 (2): 133. doi : 10.4169/college.math.j.43.2.133 . JSTOR   10.4169/college.math.j.43.2.133 . S2CID   123891402 .
  17. ^ ДеТемпл, Дуэйн В. (1992). «Треугольник наименьшего периметра, описывающий полукруг» (PDF) . Ежеквартальный журнал Фибоначчи . 30 (3): 274. МР   1175315 . Архивировано (PDF) из оригинала 20 января 2022 г. Проверено 29 января 2022 г.
  18. ^ Кочик, Ежи (январь 2019 г.). «Заметка о неограниченных упаковках аполлоновых дисков». arXiv : 1910.05924 [ math.MG ].
Викискладе есть медиафайлы по теме треугольника Кеплера .
Retrieved from "https://en.wikipedia.org/w/index.php?title=Kepler_triangle&oldid=1226849711"