Гармонический четырехугольник

В евклидовой геометрии — гармонический четырёхугольник или гармонический четырёхугольник . ^[1] — четырёхугольник , который можно вписать в окружность ( вписанный четырёхугольник ), у которой произведения длин противоположных сторон равны. Он имеет несколько важных свойств.

Свойства [ править ]

Пусть $ABCD$ — гармонический четырехугольник, $M$ середина — диагонали а $AC$ . Затем:

Касательные к описанной окружности в точках $А$ и $С$ и прямой $BD$ либо пересекаются в одной точке, либо взаимно параллельны .

Углы $∠BMC$ и $∠DMC$ равны.

Биссектрисы углов $B$ и $D$ пересекаются на диагонали $AC$ .

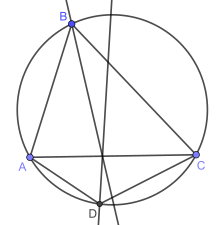
Диагональ $BD$ четырехугольника является симмедианой углов при $B$ и $D$ в треугольниках ∆ $ABC$ и ∆ $ADC$ .
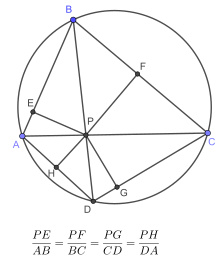
Точка пересечения диагоналей расположена по направлению к сторонам четырехугольника на расстояния, пропорциональные длинам этих сторон.

Ссылки [ править ]

^ Джонсон, Роджер А. (2007) [1929], Advanced Euclidean Geometry , Dover, p. 100, ISBN 978-0-486-46237-0

Дальнейшее чтение [ править ]

Галлатли, В. «Гармонический четырехугольник». §124 в «Современной геометрии треугольника», 2-е изд. Лондон: Ходжсон, стр. 90 и 92, 1913.

Эта посвященная геометрии, статья, незавершена . Вы можете помочь Википедии, расширив ее .

[1] Джонсон, Роджер А. (2007) [1929], Advanced Euclidean Geometry , Dover, p. 100, ISBN 978-0-486-46237-0

[1]