Параллелограмм

Параллелограмм
Параллелограмм
	Этот параллелограмм является ромбоидом, так как у него нет прямых углов и неравных сторон.
Тип	четырехугольник , трапеция
Ребра и вершины	4
Группа симметрии	С 2 , [2] + ,
Область	b × h (основание×высота); ; ab sin θ (произведение смежных сторон и синуса определяемого ими угла при вершине)
Характеристики	выпуклый

В евклидовой геометрии параллелограмм — это простой (несамопересекающийся ) четырёхугольник с двумя парами параллельных сторон. Противоположные или обращенные стороны параллелограмма имеют одинаковую длину, а противоположные углы параллелограмма имеют одинаковую длину. Сравнение , и ни одно условие не противоположных сторон и противоположных углов является прямым следствием постулата евклидовой параллельности может быть доказано без обращения к постулату евклидовой параллельности или одной из его эквивалентных формулировок.

Для сравнения, четырехугольник, по крайней мере, с одной парой параллельных сторон, представляет собой трапецию в американском английском или трапецию в британском английском.

Трехмерным аналогом параллелограмма является параллелепипед .

Слово происходит от греческого παραλληλό-γραμμον, parallēló-grammon , что означает форму «параллельных линий».

Особые случаи [ править ]

Прямоугольник – параллелограмм с четырьмя углами одинаковой величины (прямыми углами).
Ромб – параллелограмм с четырьмя сторонами одинаковой длины. Любой параллелограмм, не являющийся ни прямоугольником, ни ромбом, традиционно назывался ромбоидом, но в современной математике этот термин не используется. ^[1]
Квадрат – параллелограмм с четырьмя сторонами одинаковой длины и углами одинаковой величины (прямыми углами).

Характеристики [ править ]

Простой верно (несамопересекающийся) четырехугольник является параллелограммом тогда и только тогда, когда любое из следующих утверждений: ^[2]^[3]

Две пары противоположных сторон параллельны (по определению).
Две пары противоположных сторон равны по длине.
Две пары противоположных углов равны по мере.
Диагонали . делят друг друга пополам
Одна пара противоположных сторон параллельна и равна по длине.
Соседние углы являются дополнительными .
Каждая диагональ делит четырёхугольник на два равных треугольника .
Сумма квадратов сторон равна сумме квадратов диагоналей. (Это закон параллелограмма .)
Имеет вращательную симметрию второго порядка.
Сумма расстояний от любой внутренней точки до сторон не зависит от местоположения точки. ^[4] (Это расширение теоремы Вивиани .)
существует точка X В плоскости четырехугольника , свойство которой состоит в том, что каждая прямая, проходящая через X, делит четырехугольник на две области равной площади. ^[5]

Таким образом, все параллелограммы обладают всеми перечисленными выше свойствами, и наоборот , если хотя бы одно из этих утверждений верно в простом четырехугольнике, то это параллелограмм.

Другая недвижимость [ править ]

Противоположные стороны параллелограмма параллельны (по определению) и поэтому никогда не пересекаются.
Площадь параллелограмма в два раза больше площади треугольника, образованного одной из его диагоналей.
Площадь параллелограмма также равна величине векторного произведения двух соседних сторон.
Любая линия, проходящая через середину параллелограмма, делит площадь пополам. ^[6]
Любое невырожденное аффинное преобразование переводит параллелограмм в другой параллелограмм.
Параллелограмм имеет вращательную симметрию второго порядка (до 180°) (или порядка 4, если квадрат). Если он также имеет ровно две линии отражательной симметрии , то он должен быть ромбом или продолговатым (неквадратным прямоугольником). Если он имеет четыре линии отражательной симметрии, это квадрат .
Периметр параллелограмма равен 2( a + b ), где a и b — длины соседних сторон.
В отличие от любого другого выпуклого многоугольника, параллелограмм нельзя вписать в любой треугольник, площадь которого меньше удвоенной. ^[7]
Центры четырех квадратов, построенных либо внутри, либо снаружи на сторонах параллелограмма, являются вершинами квадрата. ^[8]
Если две прямые, параллельные сторонам параллелограмма, построены одновременно с диагональю, то параллелограммы, образованные на противоположных сторонах этой диагонали, равны по площади. ^[8]
Диагонали параллелограмма делят его на четыре треугольника одинаковой площади.

Формула площади [ править ]

Схема, показывающая, как параллелограмм можно преобразовать в форму прямоугольника. — Параллелограмм можно переставить в прямоугольник той же площади.

Все формулы площади четырехугольников общего вида применимы и к параллелограммам. Дальнейшие формулы специфичны для параллелограммов:

Параллелограмм с основанием b и высотой h можно разделить на трапецию и прямоугольный треугольник и перестроить в прямоугольник , как показано на рисунке слева. Это означает, что площадь параллелограмма такая же, как и у прямоугольника с тем же основанием и высотой:

K=bh.

Формулу площади основания × высоты также можно вывести, используя рисунок справа. Площадь K параллелограмма справа (синяя область) равна общей площади прямоугольника за вычетом площади двух оранжевых треугольников. Площадь прямоугольника равна

K_{\text{rect}}=(B+A)\times H\,

а площадь одного треугольника равна

K_{\text{tri}}={\frac {A}{2}}\times H.\,

Следовательно, площадь параллелограмма равна

K=K_{\text{rect}}-2\times K_{\text{tri}}=((B+A)\times H)-(A\times H)=B\times H.

Другая формула площади для двух сторон B и C и угла θ:

K=B\cdot C\cdot \sin \theta .\,

Площадь параллелограмма со сторонами B и C ( B ≠ C ) и углом $\gamma$ на пересечении диагоналей определяется выражением ^[9]

K={\frac {|\tan \gamma |}{2}}\cdot \left|B^{2}-C^{2}\right|.

Если параллелограмм задан исходя из длин B и C двух соседних сторон вместе с длиной D ₁ любой диагонали, то площадь можно найти по формуле Герона . В частности, это

K=2{\sqrt {S(S-B)(S-C)(S-D_{1})}}

где $S=(B+C+D_{1})/2$ а ведущий множитель 2 обусловлен тем, что выбранная диагональ делит параллелограмм на два равных треугольника.

Из координат вершин [ править ]

Пусть векторы $\mathbf {a} ,\mathbf {b} \in \mathbb {R} ^{2}$ и разреши $V={\begin{bmatrix}a_{1}&a_{2}\\b_{1}&b_{2}\end{bmatrix}}\in \mathbb {R} ^{2\times 2}$ обозначаем матрицу с элементами a и b . Тогда площадь параллелограмма, порожденного a и b , равна $|\det(V)|=|a_{1}b_{2}-a_{2}b_{1}|\,$ .

Пусть векторы $\mathbf {a} ,\mathbf {b} \in \mathbb {R} ^{n}$ и разреши $V={\begin{bmatrix}a_{1}&a_{2}&\dots &a_{n}\\b_{1}&b_{2}&\dots &b_{n}\end{bmatrix}}\in \mathbb {R} ^{2\times n}$ . Тогда площадь параллелограмма, порожденного a и b , равна ${\sqrt {\det(VV^{\mathrm {T} })}}$ .

Пусть точки $a,b,c\in \mathbb {R} ^{2}$ . Тогда подписанная площадь параллелограмма с вершинами a , b и c эквивалентна определителю матрицы, построенной с использованием a , b и c в виде строк с последним столбцом, дополненным единицами следующим образом:

K=\left|{\begin{matrix}a_{1}&a_{2}&1\\b_{1}&b_{2}&1\\c_{1}&c_{2}&1\end{matrix}}\right|.

Доказательство того, что диагонали делят друг друга пополам [ править ]

Параллелограмм ABCD — Parallelogram ABCD

Чтобы доказать, что диагонали параллелограмма делят друг друга пополам, воспользуемся равными треугольниками :

\angle ABE\cong \angle CDE

(альтернативные внутренние углы равны по мере)

\angle BAE\cong \angle DCE

(альтернативные внутренние углы равны по мере) .

(поскольку это углы, которые образует трансверсаль с параллельными прямыми AB и DC ).

Кроме того, сторона AB равна длине стороны DC , поскольку противоположные стороны параллелограмма равны по длине.

Следовательно, треугольники ABE и CDE конгруэнтны (постулат ASA, два соответствующих угла и включённая сторона ).

Поэтому,

AE=CE

BE=DE.

Поскольку диагонали AC и BD делят друг друга на отрезки одинаковой длины, они делят друг друга пополам.

Отдельно, поскольку диагонали AC и BD делят друг друга пополам в точке E , точка E является серединой каждой диагонали.

Решетка из параллелограммов [ править ]

Параллелограммы могут замостить плоскость путем перемещения. Если края равны или углы прямые, симметрия решетки выше. Они представляют собой четыре решетки Браве в двух измерениях .

Решетки
Форма	Квадрат	Прямоугольник	Ромб	Ромбовидный
Система	Квадрат (четырехугольный)	Прямоугольный (орторомбический)	Центрированный прямоугольный (орторомбический)	Косой (моноклинный)
Ограничения	α=90°, а=б	α=90°	а=б	Никто
Симметрия	p4m, [4,4], порядок 8 n	pmm, [∞,2,∞], порядок 4 n		p1, [∞ ⁺,2,∞ ⁺], порядок 2 n
Форма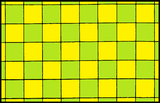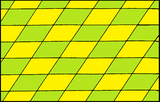

Параллелограммы, возникающие из других фигур [ править ]

Автомедиановый треугольник [ править ]

Автомедианный треугольник которого — это треугольник, медианы находятся в тех же пропорциях, что и его стороны (хотя и в другом порядке). Если ABC — автомедианный треугольник, в котором вершина A стоит напротив стороны a , G — центр тяжести (где пересекаются три медианы ABC ), а AL — одна из расширенных медиан ABC , причем L лежит на описанной окружности ABC , то BGCL — параллелограмм.

Параллелограмм Вариньона [ править ]

Теорема Вариньона утверждает, что середины сторон произвольного четырехугольника являются вершинами параллелограмма, называемого его параллелограммом Вариньона . Если четырехугольник выпуклый или вогнутый (то есть не самопересекающийся), то площадь параллелограмма Вариньона равна половине площади четырехугольника.

Доказательство без слов (см. рисунок):

Произвольный четырёхугольник и его диагонали.
Основания подобных треугольников параллельны синей диагонали.
То же самое и с красной диагональю.
Пары оснований образуют параллелограмм, у которого половина площади четырехугольника A _q равна сумме площадей четырех больших треугольников A _l равна 2 A _q (каждая из двух пар восстанавливает четырехугольник), а площадь маленького треугольников, A _s — это четверть A _l (полулинейные размеры дают четверть площади), а площадь параллелограмма равна A _q минус A _s .

Касательный параллелограмм эллипса [ править ]

Для эллипса два диаметра называются сопряженными тогда и только тогда, когда касательная к эллипсу в конечной точке одного диаметра параллельна другому диаметру. Каждая пара сопряженных диаметров эллипса имеет соответствующий касательный параллелограмм , иногда называемый ограничивающим параллелограммом, образованный касательными линиями к эллипсу в четырех конечных точках сопряженных диаметров. Все касательные параллелограммы к данному эллипсу имеют одинаковую площадь.

можно восстановить Эллипс по любой паре сопряженных диаметров или по любому касательному параллелограмму.

Грани параллелепипеда [ править ]

Параллелепипед являются – трехмерная фигура, шесть граней которой параллелограммами .

См. также [ править ]

Ссылки [ править ]

^ «CIMT — страница больше недоступна на серверах Плимутского университета» (PDF) . www.cimt.plymouth.ac.uk . Архивировано из оригинала (PDF) 14 мая 2014 г.
^ Оуэн Байер, Феликс Лазебник и Дейдра Смельцер , Методы евклидовой геометрии , Математическая ассоциация Америки, 2010, стр. 51-52.
^ Залман Усискин и Дженнифер Гриффин, «Классификация четырехугольников. Исследование определения», Information Age Publishing, 2008, стр. 22.
^ Чен, Чжибо и Лян, Тянь. «Обратная теорема Вивиани», The College Mathematics Journal 37 (5), 2006, стр. 390–391.
^ Задача 5, Британская математическая олимпиада 2006 г. , [1] .
^ Данн, Дж. А. и Дж. Э. Претти, «Разделение треугольника пополам», Mathematical Gazette 56, май 1972 г., стр. 105.
^ Вайсштейн, Эрик В. «Описание треугольника» . Математический мир Вольфрама .
^ Перейти обратно: ^а ^б Вайсштейн, Эрик В. «Параллелограмм». Из MathWorld — веб-ресурса Wolfram. http://mathworld.wolfram.com/Parallelogram.html
^ Митчелл, Дуглас В., «Площадь четырехугольника», Mathematical Gazette , июль 2009 г.

Внешние ссылки [ править ]

Параллелограмм и Ромб - Анимационный курс (Построение, Окружность, Площадь)
Вайсштейн, Эрик В. «Параллелограмм» . Математический мир .
Интерактивный параллелограмм — стороны, углы и наклон.
Площадь параллелограмма при разрезании узла
Равносторонние треугольники на сторонах параллелограмма при разрезании узла
Определение и свойства параллелограмма с анимированным апплетом
расчета площади параллелограмма Интерактивный апплет, показывающий интерактивный апплет

[1] «CIMT — страница больше недоступна на серверах Плимутского университета» (PDF) . www.cimt.plymouth.ac.uk . Архивировано из оригинала (PDF) 14 мая 2014 г.

[2] Оуэн Байер, Феликс Лазебник и Дейдра Смельцер , Методы евклидовой геометрии , Математическая ассоциация Америки, 2010, стр. 51-52.

[3] Залман Усискин и Дженнифер Гриффин, «Классификация четырехугольников. Исследование определения», Information Age Publishing, 2008, стр. 22.

[4] Чен, Чжибо и Лян, Тянь. «Обратная теорема Вивиани», The College Mathematics Journal 37 (5), 2006, стр. 390–391.

[5] Задача 5, Британская математическая олимпиада 2006 г. , [1] .

[6] Данн, Дж. А. и Дж. Э. Претти, «Разделение треугольника пополам», Mathematical Gazette 56, май 1972 г., стр. 105.

[7] Вайсштейн, Эрик В. «Описание треугольника» . Математический мир Вольфрама .

[Weisstein-8] Перейти обратно: ^а ^б Вайсштейн, Эрик В. «Параллелограмм». Из MathWorld — веб-ресурса Wolfram. http://mathworld.wolfram.com/Parallelogram.html

[9] Митчелл, Дуглас В., «Площадь четырехугольника», Mathematical Gazette , июль 2009 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]