Эллипс

Эта статья о геометрической фигуре. Чтобы узнать о других значениях, см. Эллипс (значения) .

Не путать с Ellipsis или Eclipse .

Эллипс (красный), полученный в результате пересечения конуса наклонной плоскостью.

Эллипс: обозначения

Эллипсы: примеры с увеличением эксцентриситета

В математике эллипс окружающая — это плоская кривая, две фокальные точки , причем для всех точек кривой сумма двух расстояний до фокальных точек является постоянной. Он обобщает круг , который представляет собой особый тип эллипса, в котором две фокальные точки одинаковы. Удлинение эллипса измеряется его эксцентриситетом. $e$, число от $e=0$ ( предельный случай круга) до $e=1$ (предельный случай бесконечного удлинения, уже не эллипс, а парабола ).

Эллипс имеет простое алгебраическое решение для определения своей площади, но только приближения для его периметра (также известного как длина окружности ), для которого для получения точного решения требуется интегрирование.

Аналитически уравнение стандартного эллипса с центром в начале координат и шириной $2a$ и высота $2b$ является:

$${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1.$$

Предполагая $a\geq b$, фокусы $(\pm c,0)$ для ${\textstyle c={\sqrt {a^{2}-b^{2}}}}$. Стандартное параметрическое уравнение:

$$(x,y)=(a\cos(t),b\sin(t))\quad {\text{for}}\quad 0\leq t\leq 2\pi .$$

Эллипсы — это закрытый тип конического сечения : плоская кривая, описывающая пересечение конуса с плоскостью ( см. рисунок). Эллипсы имеют много общего с двумя другими формами конических сечений, параболами и гиперболами , которые являются открытыми и неограниченными . Угловое сечение прямого кругового цилиндра также является эллипсом.

Эллипс также можно определить с точки зрения одной фокальной точки и линии вне эллипса, называемой директрисой : для всех точек эллипса соотношение между расстоянием до фокуса и расстоянием до директрисы является константой. Это постоянное соотношение и есть упомянутый выше эксцентриситет:

$$e={\frac {c}{a}}={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}.$$

Эллипсы широко распространены в физике , астрономии и технике . Например, орбита каждой планеты Солнечной системы представляет собой примерно эллипс с Солнцем в одной точке фокуса (точнее, фокус — барицентр пары Солнце-планета). То же самое относится и к спутникам, вращающимся вокруг планет, и ко всем другим системам двух астрономических тел. Формы планет и звезд часто хорошо описываются эллипсоидами . Круг, рассматриваемый под боковым углом, выглядит как эллипс: то есть эллипс — это изображение круга в параллельной или перспективной проекции . Эллипс также является простейшей фигурой Лиссажу, образующейся, когда горизонтальное и вертикальное движения представляют собой синусоиды с одинаковой частотой: аналогичный эффект приводит к эллиптической поляризации света в оптике .

Название ἔλλειψις ( élleipsis , «упущение») было дано Аполлонием Пергским в его «Кониках» .

Определение как геометрическое положение точек

Эллипс: определение по сумме расстояний до фокусов

Эллипс: определение по фокусу и круговой директрисе

Эллипс можно определить геометрически как множество точек на евклидовой плоскости:

Даны две фиксированные точки $F_{1},F_{2}$ называются фокусами и расстоянием $2a$ которое больше расстояния между фокусами, эллипс представляет собой множество точек $P$ такая, что сумма расстояний $|PF_{1}|,\ |PF_{2}|$ равно $2a$:

$$E=\left\{P\in \mathbb {R} ^{2}\,\mid \,\left|PF_{2}\right|+\left|PF_{1}\right|=2a\right\}.$$

Середина $C$ Отрезок, соединяющий фокусы, называется центром эллипса. Линия, проходящая через фокусы, называется большой осью , а линия, перпендикулярная ей, проходящая через центр, — малой осью . Большая ось пересекает эллипс в двух вершинах. $V_{1},V_{2}$, которые имеют расстояние $a$ в центр. Расстояние $c$ фокусов к центру называется фокусным расстоянием или линейным эксцентриситетом. Частное $e={\tfrac {c}{a}}$ это эксцентриситет .

Дело $F_{1}=F_{2}$ дает круг и включается как особый тип эллипса.

Уравнение $\left|PF_{2}\right|+\left|PF_{1}\right|=2a$ можно посмотреть по-другому (см. рисунок):

Если $c_{2}$ это круг с центром $F_{2}$ и радиус $2a$, то расстояние до точки $P$ в круг $c_{2}$ равно расстоянию до фокуса $F_{1}$:

$$\left|PF_{1}\right|=\left|Pc_{2}\right|.$$

$c_{2}$ называется круговой директрисой (связанной с фокусом $F_{2}$) эллипса. Это свойство не следует путать с определением эллипса с использованием линии направляющей ниже.

Используя сферы Одуванчика , можно доказать, что любое сечение конуса плоскостью является эллипсом, предполагая, что плоскость не содержит вершины и имеет наклон меньше, чем у линий на конусе.

В декартовых координатах

Параметры формы:

• а : большая полуось,
• б : малая полуось,
• c : линейный эксцентриситет,
• p : полупрямая сторона (обычно $\ell$).

Стандартное уравнение

Стандартная форма эллипса в декартовых координатах предполагает, что начало координат — это центр эллипса, ось X — большая ось и:

• фокусы - это точки $F_{1}=(c,\,0),\ F_{2}=(-c,\,0)$,
• вершины $V_{1}=(a,\,0),\ V_{2}=(-a,\,0)$.

Для произвольной точки $(x,y)$ расстояние до фокуса $(c,0)$ является ${\textstyle {\sqrt {(x-c)^{2}+y^{2}}}}$ и в другой фокус ${\textstyle {\sqrt {(x+c)^{2}+y^{2}}}}$. Отсюда и точка $(x,\,y)$ находится на эллипсе всякий раз, когда:

$${\sqrt {(x-c)^{2}+y^{2}}}+{\sqrt {(x+c)^{2}+y^{2}}}=2a\ .$$

Удаление радикалов путем подходящего возведения в квадрат и использования $b^{2}=a^{2}-c^{2}$ (см. диаграмму) дает стандартное уравнение эллипса:

$${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1,$$

или, решено для y :

$$y=\pm {\frac {b}{a}}{\sqrt {a^{2}-x^{2}}}=\pm {\sqrt {\left(a^{2}-x^{2}\right)\left(1-e^{2}\right)}}.$$

Параметры ширины и высоты $a,\;b$ называются большой и малой полуосями . Верхняя и нижняя точки $V_{3}=(0,\,b),\;V_{4}=(0,\,-b)$ являются ко-вершинами . Расстояния от точки $(x,\,y)$ на эллипсе слева и справа расположены фокусы $a+ex$ и $a-ex$.

Из уравнения следует, что эллипс симметричен относительно осей координат и, следовательно, относительно начала координат.

Параметры

Главные оси

На протяжении всей статьи большая и малая полуоси обозначаются $a$ и $b$соответственно, т.е. $a\geq b>0\ .$

В принципе, каноническое уравнение эллипса ${\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1$ может иметь $a<b$ (и, следовательно, высота эллипса будет больше его ширины). Эту форму можно преобразовать в стандартную форму, транспонировав имена переменных. $x$ и $y$ и имена параметров $a$ и $b.$

Линейный эксцентриситет

Это расстояние от центра до фокуса: $c={\sqrt {a^{2}-b^{2}}}$.

Эксцентриситет

Эксцентриситет может быть выражен как:

$$e={\frac {c}{a}}={\sqrt {1-\left({\frac {b}{a}}\right)^{2}}},$$

предполагая $a>b.$ Эллипс с равными осями ( $a=b$) имеет нулевой эксцентриситет и представляет собой круг.

Полупрямая сторона

Длина хорды, проходящей через один фокус, перпендикулярно большой оси, называется широкой прямой кишкой . Половина ее — полурасширенная прямая кишка. $\ell$. Расчет показывает:

$$\ell ={\frac {b^{2}}{a}}=a\left(1-e^{2}\right).$$

Полупрямая сторона $\ell$ равен радиусу кривизны в вершинах (см. раздел кривизна ).

Касательная

Произвольная линия $g$ пересекает эллипс в 0, 1 или 2 точках, называемых соответственно внешней линией , касательной и секущей . Через любую точку эллипса проходит единственная касательная. Касательная в точке $(x_{1},\,y_{1})$ эллипса ${\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1$ имеет координатное уравнение:

$${\frac {x_{1}}{a^{2}}}x+{\frac {y_{1}}{b^{2}}}y=1.$$

Векторное параметрическое уравнение касательной имеет вид:

$${\vec {x}}={\begin{pmatrix}x_{1}\\y_{1}\end{pmatrix}}+s\left({\begin{array}{r}-y_{1}a^{2}\\x_{1}b^{2}\end{array}}\right),\quad s\in \mathbb {R} .$$

Доказательство: Позволять $(x_{1},\,y_{1})$ быть точкой на эллипсе и ${\textstyle {\vec {x}}={\begin{pmatrix}x_{1}\\y_{1}\end{pmatrix}}+s{\begin{pmatrix}u\\v\end{pmatrix}}}$ быть уравнением любой прямой $g$ содержащий $(x_{1},\,y_{1})$. Вставляя уравнение прямой в уравнение эллипса и соблюдая ${\textstyle {\frac {x_{1}^{2}}{a^{2}}}+{\frac {y_{1}^{2}}{b^{2}}}=1}$ дает:

$${\frac {\left(x_{1}+su\right)^{2}}{a^{2}}}+{\frac {\left(y_{1}+sv\right)^{2}}{b^{2}}}=1\ \quad \Longrightarrow \quad 2s\left({\frac {x_{1}u}{a^{2}}}+{\frac {y_{1}v}{b^{2}}}\right)+s^{2}\left({\frac {u^{2}}{a^{2}}}+{\frac {v^{2}}{b^{2}}}\right)=0\ .$$

Тогда бывают случаи:

1. ${\frac {x_{1}}{a^{2}}}u+{\frac {y_{1}}{b^{2}}}v=0.$ Затем линия $g$ и эллипс имеет только точку $(x_{1},\,y_{1})$ совместно, и $g$ является касательной. Направление касательной имеет перпендикулярный вектор ${\begin{pmatrix}{\frac {x_{1}}{a^{2}}}&{\frac {y_{1}}{b^{2}}}\end{pmatrix}}$, поэтому касательная имеет уравнение ${\textstyle {\frac {x_{1}}{a^{2}}}x+{\tfrac {y_{1}}{b^{2}}}y=k}$ для некоторых $k$. Потому что $(x_{1},\,y_{1})$ находится на касательной и эллипсе, получаем $k=1$.
2. ${\frac {x_{1}}{a^{2}}}u+{\frac {y_{1}}{b^{2}}}v\neq 0.$ Затем линия $g$ имеет вторую общую точку с эллипсом и является секущей.

Используя (1), находим, что ${\begin{pmatrix}-y_{1}a^{2}&x_{1}b^{2}\end{pmatrix}}$ является касательным вектором в точке $(x_{1},\,y_{1})$, что доказывает векторное уравнение.

Если $(x_{1},y_{1})$ и $(u,v)$ две точки эллипса такие, что ${\textstyle {\frac {x_{1}u}{a^{2}}}+{\tfrac {y_{1}v}{b^{2}}}=0}$, то точки лежат на двух сопряженных диаметрах (см. ниже ). (Если $a=b$, эллипс представляет собой круг, а «сопряженный» означает «ортогональный».)

Сдвинутый эллипс

Если стандартный эллипс сдвинут в центр $\left(x_{\circ },\,y_{\circ }\right)$, его уравнение

$${\frac {\left(x-x_{\circ }\right)^{2}}{a^{2}}}+{\frac {\left(y-y_{\circ }\right)^{2}}{b^{2}}}=1\ .$$

Оси по-прежнему параллельны осям x и y .

Общий эллипс

Основная статья: Матричное представление конических сечений

Общий эллипс на плоскости можно однозначно описать как двумерное квадратное уравнение декартовых координат или с помощью центральной, большой и малой полуосей и угла

В аналитической геометрии эллипс определяется как квадрика : множество точек $(x,\,y)$ декартовой плоскости , которые в невырожденных случаях удовлетворяют неявному уравнению

$$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$$

предоставил $B^{2}-4AC<0.$

Чтобы отличить вырожденные случаи от невырожденных, пусть ∆ будет определителем

$$\Delta ={\begin{vmatrix}A&{\frac {1}{2}}B&{\frac {1}{2}}D\\{\frac {1}{2}}B&C&{\frac {1}{2}}E\\{\frac {1}{2}}D&{\frac {1}{2}}E&F\end{vmatrix}}=ACF+{\tfrac {1}{4}}BDE-{\tfrac {1}{4}}(AE^{2}+CD^{2}+FB^{2}).$$

Тогда эллипс является невырожденным вещественным эллипсом тогда и только тогда, когда C∆ < 0. Если C∆ > 0, то мы имеем мнимый эллипс, а если ∆ = 0, то имеем точечный эллипс.

Коэффициенты общего уравнения можно получить по известной большой полуоси. $a$, малая полуось $b$, координаты центра $\left(x_{\circ },\,y_{\circ }\right)$, и угол поворота $\theta$ (угол между положительной горизонтальной осью и большой осью эллипса) по формулам:

$${\begin{aligned}A&=a^{2}\sin ^{2}\theta +b^{2}\cos ^{2}\theta &B&=2\left(b^{2}-a^{2}\right)\sin \theta \cos \theta \\[1ex]C&=a^{2}\cos ^{2}\theta +b^{2}\sin ^{2}\theta &D&=-2Ax_{\circ }-By_{\circ }\\[1ex]E&=-Bx_{\circ }-2Cy_{\circ }&F&=Ax_{\circ }^{2}+Bx_{\circ }y_{\circ }+Cy_{\circ }^{2}-a^{2}b^{2}.\end{aligned}}$$

Эти выражения можно вывести из канонического уравнения

$${\frac {X^{2}}{a^{2}}}+{\frac {Y^{2}}{b^{2}}}=1$$

евклидовым преобразованием координат $(X,\,Y)$:

$${\begin{aligned}X&=\left(x-x_{\circ }\right)\cos \theta +\left(y-y_{\circ }\right)\sin \theta ,\\Y&=-\left(x-x_{\circ }\right)\sin \theta +\left(y-y_{\circ }\right)\cos \theta .\end{aligned}}$$

И наоборот, параметры канонической формы могут быть получены из коэффициентов общего вида по уравнениям:

$${\begin{aligned}a,b&={\frac {-{\sqrt {2{\big (}AE^{2}+CD^{2}-BDE+(B^{2}-4AC)F{\big )}{\big (}(A+C)\pm {\sqrt {(A-C)^{2}+B^{2}}}{\big )}}}}{B^{2}-4AC}},\\x_{\circ }&={\frac {2CD-BE}{B^{2}-4AC}},\\[5mu]y_{\circ }&={\frac {2AE-BD}{B^{2}-4AC}},\\[5mu]\theta &={\tfrac {1}{2}}\operatorname {atan2} (-B,\,C-A),\end{aligned}}$$

где atan2 — арктангенс с двумя аргументами.

Параметрическое представление

Построение точек на основе параметрического уравнения и интерпретации параметра t , предложенной де ла Гиром

Точки эллипса, рассчитанные по рациональному представлению с равноотстоящими друг от друга параметрами ( $\Delta u=0.2$).

Стандартное параметрическое представление

Используя тригонометрические функции , параметрическое представление стандартного эллипса ${\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1$ является:

$$(x,\,y)=(a\cos t,\,b\sin t),\ 0\leq t<2\pi \,.$$

Параметр t (называемый в астрономии эксцентрической аномалией ) не является углом $(x(t),y(t))$ с осью x , но имеет геометрическое значение благодаря Филиппу де Ла Гиру (см. § Рисование эллипсов ниже).

Рациональное представление

С заменой ${\textstyle u=\tan \left({\frac {t}{2}}\right)}$ и тригонометрические формулы, получаем

$$\cos t={\frac {1-u^{2}}{1+u^{2}}}\ ,\quad \sin t={\frac {2u}{1+u^{2}}}$$

и рациональное параметрическое уравнение эллипса

$${\begin{cases}x(u)=a\,{\dfrac {1-u^{2}}{1+u^{2}}}\\[10mu]y(u)=b\,{\dfrac {2u}{1+u^{2}}}\\[10mu]-\infty <u<\infty \end{cases}}$$

который покрывает любую точку эллипса ${\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1$ кроме левой вершины $(-a,\,0)$.

Для $u\in [0,\,1],$ эта формула представляет правую верхнюю четверть эллипса, движущуюся против часовой стрелки с увеличением $u.$ Левая вершина — предел ${\textstyle \lim _{u\to \pm \infty }(x(u),\,y(u))=(-a,\,0)\;.}$

Альтернативно, если параметр $[u:v]$ считается точкой на действительной проективной прямой ${\textstyle \mathbf {P} (\mathbf {R} )}$, то соответствующая рациональная параметризация равна

$$[u:v]\mapsto \left(a{\frac {v^{2}-u^{2}}{v^{2}+u^{2}}},b{\frac {2uv}{v^{2}+u^{2}}}\right).$$

Затем ${\textstyle [1:0]\mapsto (-a,\,0).}$

Рациональные представления конических сечений обычно используются в компьютерном проектировании (см. Кривую Безье ).

Наклон касательной как параметр

Параметрическое представление, использующее наклон $m$ касательная в точке эллипсаможно получить из производной стандартного представления ${\vec {x}}(t)=(a\cos t,\,b\sin t)^{\mathsf {T}}$:

$${\vec {x}}'(t)=(-a\sin t,\,b\cos t)^{\mathsf {T}}\quad \rightarrow \quad m=-{\frac {b}{a}}\cot t\quad \rightarrow \quad \cot t=-{\frac {ma}{b}}.$$

С помощью тригонометрических формул получаем:

$$\cos t={\frac {\cot t}{\pm {\sqrt {1+\cot ^{2}t}}}}={\frac {-ma}{\pm {\sqrt {m^{2}a^{2}+b^{2}}}}}\ ,\quad \quad \sin t={\frac {1}{\pm {\sqrt {1+\cot ^{2}t}}}}={\frac {b}{\pm {\sqrt {m^{2}a^{2}+b^{2}}}}}.$$

Замена $\cos t$ и $\sin t$ стандартного представления дает:

$${\vec {c}}_{\pm }(m)=\left(-{\frac {ma^{2}}{\pm {\sqrt {m^{2}a^{2}+b^{2}}}}},\;{\frac {b^{2}}{\pm {\sqrt {m^{2}a^{2}+b^{2}}}}}\right),\,m\in \mathbb {R} .$$

Здесь $m$ - наклон касательной в соответствующей точке эллипса, ${\vec {c}}_{+}$ является верхним и ${\vec {c}}_{-}$ нижняя половина эллипса. Вершины $(\pm a,\,0)$, имеющие вертикальные касательные, не покрываются изображением.

Уравнение касательной в точке ${\vec {c}}_{\pm }(m)$ имеет форму $y=mx+n$. Все еще неизвестное $n$ можно определить, вставив координаты соответствующей точки эллипса ${\vec {c}}_{\pm }(m)$:

$$y=mx\pm {\sqrt {m^{2}a^{2}+b^{2}}}\,.$$

Это описание касательных эллипса является важным инструментом для определения ортоптики эллипса . Ортоптическая статья содержит еще одно доказательство, без дифференциального исчисления и тригонометрических формул.

Общий эллипс

Эллипс как аффинное изображение единичного круга

Другое определение эллипса использует аффинные преобразования :

Любой эллипс является аффинным изображением единичной окружности с уравнением $x^{2}+y^{2}=1$.

Параметрическое представление

Аффинное преобразование евклидовой плоскости имеет вид ${\vec {x}}\mapsto {\vec {f}}\!_{0}+A{\vec {x}}$, где $A$ — регулярная матрица (с ненулевым определителем ) и ${\vec {f}}\!_{0}$ — произвольный вектор. Если ${\vec {f}}\!_{1},{\vec {f}}\!_{2}$ – векторы-столбцы матрицы $A$, единичный круг $(\cos(t),\sin(t))$, $0\leq t\leq 2\pi$, отображается на эллипс:

$${\vec {x}}={\vec {p}}(t)={\vec {f}}\!_{0}+{\vec {f}}\!_{1}\cos t+{\vec {f}}\!_{2}\sin t\,.$$

Здесь ${\vec {f}}\!_{0}$ является центром и ${\vec {f}}\!_{1},\;{\vec {f}}\!_{2}$ являются направлениями двух сопряженных диаметров , вообще говоря, не перпендикулярными.

Вершины

Четыре вершины эллипса ${\vec {p}}(t_{0}),\;{\vec {p}}\left(t_{0}\pm {\tfrac {\pi }{2}}\right),\;{\vec {p}}\left(t_{0}+\pi \right)$, для параметра $t=t_{0}$ определяется:

$$\cot(2t_{0})={\frac {{\vec {f}}\!_{1}^{\,2}-{\vec {f}}\!_{2}^{\,2}}{2{\vec {f}}\!_{1}\cdot {\vec {f}}\!_{2}}}.$$

(Если ${\vec {f}}\!_{1}\cdot {\vec {f}}\!_{2}=0$, затем $t_{0}=0$.) Это получается следующим образом. Касательный вектор в точке ${\vec {p}}(t)$ является:

$${\vec {p}}\,'(t)=-{\vec {f}}\!_{1}\sin t+{\vec {f}}\!_{2}\cos t\ .$$

По параметру вершины $t=t_{0}$, касательная перпендикулярна большой/малой осям, поэтому:

$$0={\vec {p}}'(t)\cdot \left({\vec {p}}(t)-{\vec {f}}\!_{0}\right)=\left(-{\vec {f}}\!_{1}\sin t+{\vec {f}}\!_{2}\cos t\right)\cdot \left({\vec {f}}\!_{1}\cos t+{\vec {f}}\!_{2}\sin t\right).$$

Расширение и применение идентичностей $\;\cos ^{2}t-\sin ^{2}t=\cos 2t,\ \ 2\sin t\cos t=\sin 2t\;$ дает уравнение для $t=t_{0}\;.$

Область

Из теоремы Аполлония (см. ниже) получаем:
Площадь эллипса $\;{\vec {x}}={\vec {f}}_{0}+{\vec {f}}_{1}\cos t+{\vec {f}}_{2}\sin t\;$ является

$$A=\pi \left|\det({\vec {f}}_{1},{\vec {f}}_{2})\right|.$$

Полуоси

С сокращениями $\;M={\vec {f}}_{1}^{2}+{\vec {f}}_{2}^{2},\ N=\left|\det({\vec {f}}_{1},{\vec {f}}_{2})\right|$ утверждения теоремы Аполлония можно записать как:

$$a^{2}+b^{2}=M,\quad ab=N\ .$$

Решая эту нелинейную систему для $a,b$ дает полуоси:

$${\begin{aligned}a&={\frac {1}{2}}({\sqrt {M+2N}}+{\sqrt {M-2N}})\\[1ex]b&={\frac {1}{2}}({\sqrt {M+2N}}-{\sqrt {M-2N}})\,.\end{aligned}}$$

Неявное представление

Решение параметрического представления для $\;\cos t,\sin t\;$ по правилу Крамера и используя $\;\cos ^{2}t+\sin ^{2}t-1=0\;$, получаем неявное представление

$$\det {\left({\vec {x}}\!-\!{\vec {f}}\!_{0},{\vec {f}}\!_{2}\right)^{2}}+\det {\left({\vec {f}}\!_{1},{\vec {x}}\!-\!{\vec {f}}\!_{0}\right)^{2}}-\det {\left({\vec {f}}\!_{1},{\vec {f}}\!_{2}\right)^{2}}=0.$$

Обратно: если уравнение

$x^{2}+2cxy+d^{2}y^{2}-e^{2}=0\ ,$ с $\;d^{2}-c^{2}>0\;,$

эллипса с центром в начале координат, то два вектора

$${\vec {f}}_{1}={e \choose 0},\quad {\vec {f}}_{2}={\frac {e}{\sqrt {d^{2}-c^{2}}}}{-c \choose 1}$$

указывают на две сопряженные точки, и инструменты, разработанные выше, применимы.

Пример : для эллипса с уравнением $\;x^{2}+2xy+3y^{2}-1=0\;$ векторы

$${\vec {f}}_{1}={1 \choose 0},\quad {\vec {f}}_{2}={\frac {1}{\sqrt {2}}}{-1 \choose 1}.$$

Вихри: вложенные, масштабированные и повернутые эллипсы. Спираль не рисуется: мы видим ее как место точек, где эллипсы особенно близки друг к другу.

Повернутый стандартный эллипс

Для ${\vec {f}}_{0}={0 \choose 0},\;{\vec {f}}_{1}=a{\cos \theta \choose \sin \theta },\;{\vec {f}}_{2}=b{-\sin \theta \choose \;\cos \theta }$ получается параметрическое представление стандартного эллипса, повернутого на угол $\theta$:

$${\begin{aligned}x&=x_{\theta }(t)=a\cos \theta \cos t-b\sin \theta \sin t\,,\\y&=y_{\theta }(t)=a\sin \theta \cos t+b\cos \theta \sin t\,.\end{aligned}}$$

Эллипс в космосе

Определение эллипса в этом разделе дает параметрическое представление произвольного эллипса, даже в пространстве, если это допускается. ${\vec {f}}\!_{0},{\vec {f}}\!_{1},{\vec {f}}\!_{2}$ быть векторами в пространстве.

Полярные формы

Полярная форма относительно центра

Полярные координаты с центром в центре.

В полярных координатах , с началом координат в центре эллипса и с угловой координатой $\theta$ если отсчитывать от большой оси, уравнение эллипса имеет вид

$$r(\theta )={\frac {ab}{\sqrt {(b\cos \theta )^{2}+(a\sin \theta )^{2}}}}={\frac {b}{\sqrt {1-(e\cos \theta )^{2}}}}$$

где $e$ это эксцентриситет, а не число Эйлера.

Полярная форма относительно фокуса

Полярные координаты в центре фокуса.

Если вместо этого мы используем полярные координаты с началом координат в одном фокусе, с угловой координатой $\theta =0$ по-прежнему измеряется от большой оси, уравнение эллипса имеет вид

$$r(\theta )={\frac {a(1-e^{2})}{1\pm e\cos \theta }}$$

где знак в знаменателе отрицательный, если исходное направление $\theta =0$ указывает на центр (как показано справа) и является положительным, если это направление указывает от центра.

Угол $\theta$ называется истинной аномалией точки. Числитель $\ell =a(1-e^{2})$ это полурасширенная прямая кишка .

Эксцентриситет и свойство директрисы

Эллипс: свойство направляющей

Каждая из двух линий параллельна малой оси и на расстоянии ${\textstyle d={\frac {a^{2}}{c}}={\frac {a}{e}}}$ отсюда называется директрисой эллипса (см. схему).

Для произвольной точки $P$ эллипса частное расстояния до одного фокуса и соответствующей директрисы (см. схему) равно эксцентриситету:

$${\frac {\left|PF_{1}\right|}{\left|Pl_{1}\right|}}={\frac {\left|PF_{2}\right|}{\left|Pl_{2}\right|}}=e={\frac {c}{a}}\ .$$

Доказательство для пары $F_{1},l_{1}$ следует из того, что ${\textstyle \left|PF_{1}\right|^{2}=(x-c)^{2}+y^{2},\ \left|Pl_{1}\right|^{2}=\left(x-{\tfrac {a^{2}}{c}}\right)^{2}}$ и $y^{2}=b^{2}-{\tfrac {b^{2}}{a^{2}}}x^{2}$ удовлетворить уравнение

$$\left|PF_{1}\right|^{2}-{\frac {c^{2}}{a^{2}}}\left|Pl_{1}\right|^{2}=0\,.$$

Второй случай доказывается аналогично.

Обратное также верно и может использоваться для определения эллипса (аналогично определению параболы):

Для любой точки $F$ (фокус), любая линия $l$ (директриса) не через $F$и любое действительное число $e$ с $0<e<1,$ эллипс — это геометрическое место точек, для которых частное расстояний до точки и прямой равно $e,$ то есть:

$$E=\left\{P\ \left|\ {\frac {|PF|}{|Pl|}}=e\right.\right\}.$$

Расширение для $e=0$, который является эксцентриситетом окружности, в данном контексте не допускается в евклидовой плоскости. Однако можно считать директрисой окружности линию, находящуюся на бесконечности в проективной плоскости .

(Выбор $e=1$ дает параболу, и если $e>1$, гипербола.)

Карандаш из коник с общей вершиной и общей полураскрытой прямой кишкой.

Доказательство

Позволять $F=(f,\,0),\ e>0$и предположим $(0,\,0)$ является точкой на кривой. Директриса $l$ имеет уравнение $x=-{\tfrac {f}{e}}$. С $P=(x,\,y)$, отношение $|PF|^{2}=e^{2}|Pl|^{2}$ выдает уравнения

$(x-f)^{2}+y^{2}=e^{2}\left(x+{\frac {f}{e}}\right)^{2}=(ex+f)^{2}$ и $x^{2}\left(e^{2}-1\right)+2xf(1+e)-y^{2}=0.$

Замена $p=f(1+e)$ урожайность

$$x^{2}\left(e^{2}-1\right)+2px-y^{2}=0.$$

Это уравнение эллипса ( $e<1$), или парабола ( $e=1$), или гипербола ( $e>1$). Все эти невырожденные коники имеют общее начало в виде вершины (см. диаграмму).

Если $e<1$, ввести новые параметры $a,\,b$ так что $1-e^{2}={\tfrac {b^{2}}{a^{2}}},{\text{ and }}\ p={\tfrac {b^{2}}{a}}$, и тогда приведенное выше уравнение принимает вид

$${\frac {(x-a)^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1\,,$$

которое представляет собой уравнение эллипса с центром $(a,\,0)$, ось X как главная ось, ибольшая/малая полуось $a,\,b$.

Построение директрисы

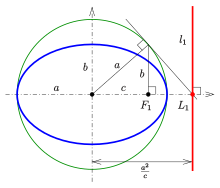
Построение директрисы

Из-за $c\cdot {\tfrac {a^{2}}{c}}=a^{2}$ точка $L_{1}$ директрисы $l_{1}$ (см. схему) и сфокусируйтесь $F_{1}$ обратны относительно инверсии окружности в окружности $x^{2}+y^{2}=a^{2}$ (на схеме зеленой). Следовательно $L_{1}$ можно построить, как показано на схеме. Директриса $l_{1}$ - перпендикуляр к главной оси в точке $L_{1}$.

Общий эллипс

Если фокус $F=\left(f_{1},\,f_{2}\right)$ и директриса $ux+vy+w=0$, получаем уравнение

$$\left(x-f_{1}\right)^{2}+\left(y-f_{2}\right)^{2}=e^{2}{\frac {\left(ux+vy+w\right)^{2}}{u^{2}+v^{2}}}\ .$$

(Правая часть уравнения использует нормальную форму линии Гессе для расчета расстояния $|Pl|$.)

Свойство отражения от фокуса к фокусу

Эллипс: касательная делит пополам дополнительный угол угла между линиями, ведущими к фокусам.

Лучи из одного фокуса отражаются от эллипса и проходят через другой фокус.

Эллипс обладает следующим свойством:

Нормальный в какой-то момент $P$ делит пополам угол между линиями ${\overline {PF_{1}}},\,{\overline {PF_{2}}}$.

Доказательство

Поскольку касательная линия перпендикулярна нормали, эквивалентным утверждением является то, что касательная является биссектрисой внешнего угла линий, ведущих к фокусам (см. Диаграмму).Позволять $L$ быть точкой на линии ${\overline {PF_{2}}}$ с расстоянием $2a$ в фокусе $F_{2}$, где $a$ — большая полуось эллипса. Пусть линия $w$ быть биссектрисой внешнего угла линий ${\overline {PF_{1}}}$ и ${\overline {PF_{2}}}.$ Возьмите любую другую точку $Q$ на $w.$ По неравенству треугольника и теореме о биссектрисе , $2a=\left|LF_{2}\right|<{}$$\left|QF_{2}\right|+\left|QL\right|={}$$\left|QF_{2}\right|+\left|QF_{1}\right|,$ поэтому $Q$ должно находиться вне эллипса. Поскольку это верно для любого выбора $Q,$ $w$ пересекает эллипс только в одной точке $P$ такой же должна быть и касательная линия.

Приложение

Лучи из одного фокуса отражаются эллипсом во второй фокус. Это свойство имеет оптическое и акустическое применение, аналогично отражающему свойству параболы (см. шепчущую галерею ).

Кроме того, из-за свойства эллипсов отражения от фокуса к фокусу, если лучам позволить продолжать распространяться, отраженные лучи в конечном итоге будут точно совмещены с большой осью.

Сопряженные диаметры

Определение

Ортогональные диаметры окружности с квадратом касательных, серединами параллельных хорд и аффинным изображением, представляющим собой эллипс с сопряженными диаметрами, параллелограмм касательных и середины хорд.

Основная статья: Сопряженные диаметры

Круг обладает следующим свойством:

Середины параллельных хорд лежат на диаметре.

Аффинное преобразование сохраняет параллельность и середины отрезков, поэтому это свойство справедливо для любого эллипса. (Обратите внимание, что параллельные хорды и диаметр больше не ортогональны.)

Определение

Два диаметра $d_{1},\,d_{2}$ эллипса сопряжены , если середины хорд параллельны $d_{1}$ лежать на $d_{2}\ .$

Из диаграммы можно найти:

Два диаметра ${\overline {P_{1}Q_{1}}},\,{\overline {P_{2}Q_{2}}}$ эллипса сопряжены, если касательные в точках $P_{1}$ и $Q_{1}$ параллельны ${\overline {P_{2}Q_{2}}}$.

Сопряженные диаметры в эллипсе обобщают ортогональные диаметры в круге.

В приведенном выше параметрическом уравнении общего эллипса

$${\vec {x}}={\vec {p}}(t)={\vec {f}}\!_{0}+{\vec {f}}\!_{1}\cos t+{\vec {f}}\!_{2}\sin t,$$

любая пара точек ${\vec {p}}(t),\ {\vec {p}}(t+\pi )$ принадлежат диаметру, а пара ${\vec {p}}\left(t+{\tfrac {\pi }{2}}\right),\ {\vec {p}}\left(t-{\tfrac {\pi }{2}}\right)$ принадлежат его сопряженному диаметру.

Для общего параметрического представления $(a\cos t,b\sin t)$ эллипса с уравнением ${\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1$ получает: Очки

$(x_{1},y_{1})=(\pm a\cos t,\pm b\sin t)\quad$ (знаки: (+,+) или (−,−))

$(x_{2},y_{2})=({\color {red}{\mp }}a\sin t,\pm b\cos t)\quad$ (знаки: (−,+) или (+,−))

являются сопряженными и

${\frac {x_{1}x_{2}}{a^{2}}}+{\frac {y_{1}y_{2}}{b^{2}}}=0\ .$

В случае круга последнее уравнение схлопывается до $x_{1}x_{2}+y_{1}y_{2}=0\ .$

Аполлония о

Теорема Аполлония

Для альтернативной формулы площади

Для эллипса с полуосями $a,\,b$ верно следующее:

Позволять $c_{1}$ и $c_{2}$ быть половинками двух сопряженных диаметров (см. диаграмму), тогда

1. $c_{1}^{2}+c_{2}^{2}=a^{2}+b^{2}$.
2. Треугольник ​ $O,P_{1},P_{2}$ с боками $c_{1},\,c_{2}$ (см. диаграмму) имеет постоянную площадь ${\textstyle A_{\Delta }={\frac {1}{2}}ab}$, что можно выразить формулой $A_{\Delta }={\tfrac {1}{2}}c_{2}d_{1}={\tfrac {1}{2}}c_{1}c_{2}\sin \alpha$, слишком. $d_{1}$ это высота точки $P_{1}$ и $\alpha$ угол между полудиаметрами. Следовательно, площадь эллипса (см. раздел « Свойства метрики» ) можно записать как $A_{el}=\pi ab=\pi c_{2}d_{1}=\pi c_{1}c_{2}\sin \alpha$.
3. Параллелограмм касательных, примыкающих к заданным сопряженным диаметрам, имеет вид ${\text{Area}}_{12}=4ab\ .$

Доказательство

Пусть эллипс имеет каноническую форму с параметрическим уравнением

$${\vec {p}}(t)=(a\cos t,\,b\sin t).$$

Две точки ${\textstyle {\vec {c}}_{1}={\vec {p}}(t),\ {\vec {c}}_{2}={\vec {p}}\left(t+{\frac {\pi }{2}}\right)}$ находятся на сопряженных диаметрах (см. предыдущий раздел). Из тригонометрических формул получаем ${\vec {c}}_{2}=(-a\sin t,\,b\cos t)^{\mathsf {T}}$ и

$$\left|{\vec {c}}_{1}\right|^{2}+\left|{\vec {c}}_{2}\right|^{2}=\cdots =a^{2}+b^{2}\,.$$

Площадь треугольника, образованного ${\vec {c}}_{1},\,{\vec {c}}_{2}$ является

$$A_{\Delta }={\tfrac {1}{2}}\det \left({\vec {c}}_{1},\,{\vec {c}}_{2}\right)=\cdots ={\tfrac {1}{2}}ab$$

Из рисунка видно, что площадь параллелограмма в 8 раз больше площади $A_{\Delta }$. Следовательно

$${\text{Area}}_{12}=4ab\,.$$

Ортогональные касательные

Эллипс с ортоптиком

Основная статья: Ортоптика (геометрия)

Для эллипса ${\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1$ точки пересечения ортогональных касательных лежат на окружности $x^{2}+y^{2}=a^{2}+b^{2}$.

Этот круг называется ортоптическим или направляющим кругом эллипса (не путать с круговой направляющей, определенной выше).

Рисование эллипсов

Центральная проекция кругов (ворота)

Эллипсы появляются в начертательной геометрии как изображения (параллельная или центральная проекция) кругов. Существуют различные инструменты для рисования эллипса. Компьютеры предоставляют самый быстрый и точный метод рисования эллипса. Однако существуют технические инструменты ( эллипсографы ), позволяющие нарисовать эллипс без компьютера. Принцип эллипсографа был известен греческим математикам, таким как Архимед и Проклос .

Если эллипсографа нет, можно нарисовать эллипс, используя аппроксимацию четырьмя соприкасающимися кругами в вершинах .

Для любого метода, описанного ниже, необходимо знание осей и полуосей (или, что то же самое: фокусов и большой полуоси). Если это предположение не выполняется, то необходимо знать как минимум два сопряженных диаметра. С помощью конструкции Ритца можно извлечь оси и полуоси.

Точечная конструкция де Ла Гира

Следующая конструкция одиночных точек эллипса принадлежит де Ла Гиру . Он основан на стандартном параметрическом представлении $(a\cos t,\,b\sin t)$ эллипса:

1. Нарисуйте два круга с центром в центре эллипса с радиусами. $a,b$ и оси эллипса.
2. Нарисуйте линию через центр , которая пересекает два круга в точке $A$ и $B$, соответственно.
3. Проведите линию через $A$ параллельно малой оси и линии, проходящей через $B$ то есть параллельно главной оси. Эти линии встречаются в точке эллипса (см. диаграмму).
4. Повторите шаги (2) и (3) с разными линиями, проходящими через центр.

• 
  метод де Ла Гира
• 
  Анимация метода

Эллипс: метод садовника

Метод булавок и веревок

Характеристика эллипса как геометрического места точек так, чтобы сумма расстояний до фокусов была постоянной, приводит к методу его рисования с использованием двух канцелярских кнопок , веревки и карандаша. В этом методе булавки втыкаются в бумагу в двух точках, которые становятся фокусами эллипса. К двум булавкам на каждом конце привязана веревка; его длина после завязывания равна $2a$. Затем кончик карандаша рисует эллипс, если его перемещать, сохраняя при этом натянутую веревку. Используя два колышка и веревку, садовники используют эту процедуру, чтобы очертить эллиптическую клумбу — поэтому ее называют эллипсом садовника .

Подобный метод рисования конфокальных эллипсов с замкнутой струной принадлежит ирландскому епископу Чарльзу Грейвсу .

полоски

Два следующих метода основаны на параметрическом представлении (см. § Стандартное параметрическое представление выше):

$$(a\cos t,\,b\sin t)$$

Технически это представление можно смоделировать двумя простыми методами. В обоих случаях центр, оси и полуоси $a,\,b$ надо знать.

Способ 1

Первый метод начинается с

полоска бумаги длиной $a+b$.

Точка пересечения полуосей отмечена знаком $P$. Если полоска скользит обоими концами по осям искомого эллипса, то точка $P$ обводит эллипс. Для доказательства показывается, что точка $P$ имеет параметрическое представление $(a\cos t,\,b\sin t)$, где параметр $t$ — угол наклона бумажной полоски.

Техническую реализацию движения бумажной полоски может осуществить пара Туси (см. анимацию). Устройство способно нарисовать любой эллипс с фиксированной суммой. $a+b$, который является радиусом большого круга. Это ограничение может оказаться недостатком в реальной жизни. Более гибким является второй метод полоски бумаги.

• 
  Построение эллипса: метод бумажной полоски 1
• 
  Эллипсы с парой Туси. Два примера: красный и голубой.

Вариант метода бумажной полоски 1 использует наблюдение, что средняя точка $N$ бумажная полоска движется по кругу с центром $M$ (эллипса) и радиус ${\tfrac {a+b}{2}}$. Следовательно, полоску бумаги можно разрезать в точке $N$ на половинки, снова соединенные суставом в $N$ и скользящий конец $K$ фиксированный в центре $M$ (см. схему). После этой операции движение неизмененной половины полоски не изменится. Для этого варианта требуется только один скользящий башмак.

• 
  Вариант метода бумажной полоски 1
• 
  Анимация варианта метода бумажной полоски 1

Построение эллипса: метод бумажной полоски 2

Способ 2

Второй метод начинается с

полоска бумаги длиной $a$.

Отмечается точка, разделяющая полосу на две подполоски длиной $b$ и $a-b$. Полоса располагается по осям, как показано на схеме. Тогда свободный конец полоски очерчивает эллипс, а полоска перемещается. Для доказательства следует признать, что точку трассировки можно описать параметрически формулой $(a\cos t,\,b\sin t)$, где параметр $t$ — угол наклона бумажной полоски.

Этот метод является основой для нескольких эллипсографов (см. раздел ниже).

Подобно варианту метода бумажных полосок 1, вариант метода бумажных полосок 2 можно создать (см. схему), разрезав часть между осями пополам.

• 
  Походка Архимеда (принцип)
• 
  Эллипсограф Бенджамина Брамера
• 
  Вариант метода бумажной полоски 2

Большинство инструментов для рисования эллипсографов основаны на втором методе полосок бумаги.

Аппроксимация эллипса соприкасающимися окружностями

Аппроксимация соприкасающимися окружностями

Из свойств метрики ниже можно получить:

• Радиус кривизны в вершинах $V_{1},\,V_{2}$ является: ${\tfrac {b^{2}}{a}}$
• Радиус кривизны в со-вершинах $V_{3},\,V_{4}$ является: ${\tfrac {a^{2}}{b}}\ .$

На схеме показан простой способ найти центры кривизны. $C_{1}=\left(a-{\tfrac {b^{2}}{a}},0\right),\,C_{3}=\left(0,b-{\tfrac {a^{2}}{b}}\right)$ в вершине $V_{1}$ и ковершина $V_{3}$, соответственно:

1. отметить вспомогательную точку $H=(a,\,b)$ и нарисуем отрезок $V_{1}V_{3}\ ,$
2. провести линию через $H$, который перпендикулярен прямой $V_{1}V_{3}\ ,$
3. точки пересечения этой линии с осями являются центрами соприкасающихся окружностей.

(доказательство: простой расчет.)

Центры остальных вершин находятся по симметрии.

С помощью кривой Френч рисуют кривую, имеющую плавный контакт с соприкасающимися окружностями .

Поколение Штейнера

Эллипс: поколение Штейнера

Эллипс: поколение Штейнера

Следующий метод построения отдельных точек эллипса основан на генерации Штейнером конического сечения :

Даны два карандаша $B(U),\,B(V)$ линий в двух точках $U,\,V$ (все строки, содержащие $U$ и $V$соответственно) и проективное, но не перспективное отображение $\pi$ из $B(U)$ на $B(V)$, то точки пересечения соответствующих прямых образуют невырожденное проективное коническое сечение.

Для генерации точек эллипса ${\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1$ каждый использует карандаши в вершинах $V_{1},\,V_{2}$. Позволять $P=(0,\,b)$ быть верхней ковершиной эллипса и $A=(-a,\,2b),\,B=(a,\,2b)$.

$P$ является центром прямоугольника $V_{1},\,V_{2},\,B,\,A$. Сторона ${\overline {AB}}$ прямоугольника разделен на n равноотстоящих друг от друга отрезков, и это деление проецируется параллельно диагонали $AV_{2}$ как направление на отрезок прямой ${\overline {V_{1}B}}$ и назначьте деление, как показано на схеме. Параллельная проекция вместе с обратной ориентацией является частью проективного отображения между пучками в точке $V_{1}$ и $V_{2}$ нужный. Точки пересечения любых двух связанных линий $V_{1}B_{i}$ и $V_{2}A_{i}$ являются точками однозначно определенного эллипса. С помощью точек $C_{1},\,\dotsc$ можно определить точки второй четверти эллипса. Аналогично получаются точки нижней половины эллипса.

Генерация Штейнера также может быть определена для гипербол и парабол. Его иногда называют методом параллелограмма, потому что вместо вершин можно использовать другие точки, которые начинаются с параллелограмма вместо прямоугольника.

Как гипотрохоид

Эллипс (красным) как частный случай гипотрохоиды с R = 2 r.

Эллипс является частным случаем гипотрохоиды , когда $R=2r$, как показано на соседнем изображении. Частный случай движущейся окружности радиуса. $r$ внутри круга с радиусом $R=2r$ называется парой Туси .

Вписанные углы и трехточечная форма

Круги

Круг: теорема о вписанном угле

Круг с уравнением $\left(x-x_{\circ }\right)^{2}+\left(y-y_{\circ }\right)^{2}=r^{2}$ однозначно определяется тремя точками $\left(x_{1},y_{1}\right),\;\left(x_{2},\,y_{2}\right),\;\left(x_{3},\,y_{3}\right)$ не на линии. Простой способ определения параметров $x_{\circ },y_{\circ },r$ использует теорему о вписанном угле для окружностей:

За четыре очка $P_{i}=\left(x_{i},\,y_{i}\right),\ i=1,\,2,\,3,\,4,\,$ (см. диаграмму) верно следующее утверждение:

Четыре точки лежат на окружности тогда и только тогда, когда углы при $P_{3}$ и $P_{4}$ равны.

Обычно вписанные углы измеряют в градусах или радианах θ , но здесь удобнее следующее измерение:

Чтобы измерить угол между двумя линиями с помощью уравнений $y=m_{1}x+d_{1},\ y=m_{2}x+d_{2},\ m_{1}\neq m_{2},$ используется частное:

$${\frac {1+m_{1}m_{2}}{m_{2}-m_{1}}}=\cot \theta \ .$$

Теорема о вписанном угле для окружностей

За четыре очка $P_{i}=\left(x_{i},\,y_{i}\right),\ i=1,\,2,\,3,\,4,\,$ нет трех из них на линии, мы имеем следующее (см. схему):

Четыре точки лежат на окружности тогда и только тогда, когда углы при $P_{3}$ и $P_{4}$ равны. С точки зрения измерения угла выше, это означает:

$${\frac {(x_{4}-x_{1})(x_{4}-x_{2})+(y_{4}-y_{1})(y_{4}-y_{2})}{(y_{4}-y_{1})(x_{4}-x_{2})-(y_{4}-y_{2})(x_{4}-x_{1})}}={\frac {(x_{3}-x_{1})(x_{3}-x_{2})+(y_{3}-y_{1})(y_{3}-y_{2})}{(y_{3}-y_{1})(x_{3}-x_{2})-(y_{3}-y_{2})(x_{3}-x_{1})}}.$$

Сначала размер доступен только для аккордов, не параллельных оси Y, но окончательная формула работает для любого аккорда.

Трехточечная форма уравнения окружности

Как следствие, получаем уравнение для окружности, определяемой тремя неколлинеарными точками $P_{i}=\left(x_{i},\,y_{i}\right)$:

$${\frac {({\color {red}x}-x_{1})({\color {red}x}-x_{2})+({\color {red}y}-y_{1})({\color {red}y}-y_{2})}{({\color {red}y}-y_{1})({\color {red}x}-x_{2})-({\color {red}y}-y_{2})({\color {red}x}-x_{1})}}={\frac {(x_{3}-x_{1})(x_{3}-x_{2})+(y_{3}-y_{1})(y_{3}-y_{2})}{(y_{3}-y_{1})(x_{3}-x_{2})-(y_{3}-y_{2})(x_{3}-x_{1})}}.$$

Например, для $P_{1}=(2,\,0),\;P_{2}=(0,\,1),\;P_{3}=(0,\,0)$ уравнение трех точек:

${\frac {(x-2)x+y(y-1)}{yx-(y-1)(x-2)}}=0$, который можно переставить в $(x-1)^{2}+\left(y-{\tfrac {1}{2}}\right)^{2}={\tfrac {5}{4}}\ .$

Используя векторы, скалярные произведения и определители, эту формулу можно представить более наглядно, позволяя ${\vec {x}}=(x,\,y)$:

$${\frac {\left({\color {red}{\vec {x}}}-{\vec {x}}_{1}\right)\cdot \left({\color {red}{\vec {x}}}-{\vec {x}}_{2}\right)}{\det \left({\color {red}{\vec {x}}}-{\vec {x}}_{1},{\color {red}{\vec {x}}}-{\vec {x}}_{2}\right)}}={\frac {\left({\vec {x}}_{3}-{\vec {x}}_{1}\right)\cdot \left({\vec {x}}_{3}-{\vec {x}}_{2}\right)}{\det \left({\vec {x}}_{3}-{\vec {x}}_{1},{\vec {x}}_{3}-{\vec {x}}_{2}\right)}}.$$

Центр круга $\left(x_{\circ },\,y_{\circ }\right)$ удовлетворяет:

$${\begin{bmatrix}1&{\dfrac {y_{1}-y_{2}}{x_{1}-x_{2}}}\\[2ex]{\dfrac {x_{1}-x_{3}}{y_{1}-y_{3}}}&1\end{bmatrix}}{\begin{bmatrix}x_{\circ }\\[1ex]y_{\circ }\end{bmatrix}}={\begin{bmatrix}{\dfrac {x_{1}^{2}-x_{2}^{2}+y_{1}^{2}-y_{2}^{2}}{2(x_{1}-x_{2})}}\\[2ex]{\dfrac {y_{1}^{2}-y_{3}^{2}+x_{1}^{2}-x_{3}^{2}}{2(y_{1}-y_{3})}}\end{bmatrix}}.$$

Радиус — это расстояние между любой из трех точек и центром.

$$r={\sqrt {\left(x_{1}-x_{\circ }\right)^{2}+\left(y_{1}-y_{\circ }\right)^{2}}}={\sqrt {\left(x_{2}-x_{\circ }\right)^{2}+\left(y_{2}-y_{\circ }\right)^{2}}}={\sqrt {\left(x_{3}-x_{\circ }\right)^{2}+\left(y_{3}-y_{\circ }\right)^{2}}}.$$

Эллипсы

В этом разделе рассматривается семейство эллипсов, определяемое уравнениями ${\tfrac {\left(x-x_{\circ }\right)^{2}}{a^{2}}}+{\tfrac {\left(y-y_{\circ }\right)^{2}}{b^{2}}}=1$ с фиксированным эксцентриситетом $e$. Удобно использовать параметр:

$${\color {blue}q}={\frac {a^{2}}{b^{2}}}={\frac {1}{1-e^{2}}},$$

и записать уравнение эллипса как:

$$\left(x-x_{\circ }\right)^{2}+{\color {blue}q}\,\left(y-y_{\circ }\right)^{2}=a^{2},$$

где q фиксировано и $x_{\circ },\,y_{\circ },\,a$ отличаться от реальных цифр. (Оси таких эллипсов параллельны осям координат: если $q<1$, большая ось параллельна оси x ; если $q>1$, оно параллельно оси y .)

Теорема о вписанном угле эллипса

Как и круг, такой эллипс определяется тремя точками, не лежащими на прямой.

Для этого семейства эллипсов вводится следующая q-аналоговая угловая мера, которая не является функцией обычной угловой меры θ :

Чтобы измерить угол между двумя линиями с помощью уравнений $y=m_{1}x+d_{1},\ y=m_{2}x+d_{2},\ m_{1}\neq m_{2}$ используется частное:

$${\frac {1+{\color {blue}q}\;m_{1}m_{2}}{m_{2}-m_{1}}}\ .$$

угле для эллипсов

Учитывая четыре балла $P_{i}=\left(x_{i},\,y_{i}\right),\ i=1,\,2,\,3,\,4$, не три из них на линии (см. схему).

Четыре точки находятся на эллипсе с уравнением $(x-x_{\circ })^{2}+{\color {blue}q}\,(y-y_{\circ })^{2}=a^{2}$ тогда и только тогда, когда углы при $P_{3}$ и $P_{4}$ равны в смысле измерения, приведенного выше, то есть, если

$${\frac {(x_{4}-x_{1})(x_{4}-x_{2})+{\color {blue}q}\;(y_{4}-y_{1})(y_{4}-y_{2})}{(y_{4}-y_{1})(x_{4}-x_{2})-(y_{4}-y_{2})(x_{4}-x_{1})}}={\frac {(x_{3}-x_{1})(x_{3}-x_{2})+{\color {blue}q}\;(y_{3}-y_{1})(y_{3}-y_{2})}{(y_{3}-y_{1})(x_{3}-x_{2})-(y_{3}-y_{2})(x_{3}-x_{1})}}\ .$$

Сначала размер доступен только для хорд, не параллельных оси Y. Но окончательная формула работает для любого аккорда. Доказательство следует из несложного расчета. Для направления доказательства, учитывая, что точки лежат на эллипсе, можно предположить, что центр эллипса является началом координат.

Трехточечная

Как следствие, получаем уравнение для эллипса, определяемого тремя неколлинеарными точками $P_{i}=\left(x_{i},\,y_{i}\right)$:

$${\frac {({\color {red}x}-x_{1})({\color {red}x}-x_{2})+{\color {blue}q}\;({\color {red}y}-y_{1})({\color {red}y}-y_{2})}{({\color {red}y}-y_{1})({\color {red}x}-x_{2})-({\color {red}y}-y_{2})({\color {red}x}-x_{1})}}={\frac {(x_{3}-x_{1})(x_{3}-x_{2})+{\color {blue}q}\;(y_{3}-y_{1})(y_{3}-y_{2})}{(y_{3}-y_{1})(x_{3}-x_{2})-(y_{3}-y_{2})(x_{3}-x_{1})}}\ .$$

Например, для $P_{1}=(2,\,0),\;P_{2}=(0,\,1),\;P_{3}=(0,\,0)$ и $q=4$ получается трехточечная форма

${\frac {(x-2)x+4y(y-1)}{yx-(y-1)(x-2)}}=0$ и после конвертации ${\frac {(x-1)^{2}}{2}}+{\frac {\left(y-{\frac {1}{2}}\right)^{2}}{\frac {1}{2}}}=1.$

Аналогично случаю с кругом, уравнение можно записать более наглядно, используя векторы:

$${\frac {\left({\color {red}{\vec {x}}}-{\vec {x}}_{1}\right)*\left({\color {red}{\vec {x}}}-{\vec {x}}_{2}\right)}{\det \left({\color {red}{\vec {x}}}-{\vec {x}}_{1},{\color {red}{\vec {x}}}-{\vec {x}}_{2}\right)}}={\frac {\left({\vec {x}}_{3}-{\vec {x}}_{1}\right)*\left({\vec {x}}_{3}-{\vec {x}}_{2}\right)}{\det \left({\vec {x}}_{3}-{\vec {x}}_{1},{\vec {x}}_{3}-{\vec {x}}_{2}\right)}},$$

где $*$ это модифицированное скалярное произведение ${\vec {u}}*{\vec {v}}=u_{x}v_{x}+{\color {blue}q}\,u_{y}v_{y}.$

Полюсно-полярное соотношение

Эллипс: полюс-полярное соотношение

Любой эллипс можно описать в подходящей системе координат уравнением ${\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1$. Уравнение касательной в точке $P_{1}=\left(x_{1},\,y_{1}\right)$ эллипса ${\tfrac {x_{1}x}{a^{2}}}+{\tfrac {y_{1}y}{b^{2}}}=1.$ Если допустить точку $P_{1}=\left(x_{1},\,y_{1}\right)$ быть произвольной точкой, отличной от начала координат, то

точка $P_{1}=\left(x_{1},\,y_{1}\right)\neq (0,\,0)$ отображается на линии ${\tfrac {x_{1}x}{a^{2}}}+{\tfrac {y_{1}y}{b^{2}}}=1$, а не через центр эллипса.

Это отношение между точками и линиями является биекцией .

функция Обратная отображает

• линия $y=mx+d,\ d\neq 0$ в точку $\left(-{\tfrac {ma^{2}}{d}},\,{\tfrac {b^{2}}{d}}\right)$ и
• линия $x=c,\ c\neq 0$ в точку $\left({\tfrac {a^{2}}{c}},\,0\right).$

Такое отношение между точками и линиями, порожденное коникой, называется полюсно-полярным отношением или полярностью . Полюс — это точка; полярная линия.

Расчетным путем можно подтвердить следующие свойства полюсно-полярного отношения эллипса:

• Для точки (полюса) на эллипсе полярой является касательная в этой точке (см. схему: $P_{1},\,p_{1}$).
• Для шеста $P$ вне эллипса точки пересечения его поляры с эллипсом являются точками касания двух касательных, проходящих $P$ (см. схему: $P_{2},\,p_{2}$).
• Для точки внутри эллипса поляра не имеет общей точки с эллипсом (см. диаграмму: $F_{1},\,l_{1}$).

1. Точкой пересечения двух поляров является полюс линии, проходящей через их полюса.
2. Очаги $(c,\,0)$ и $(-c,\,0)$соответственно и директрисы $x={\tfrac {a^{2}}{c}}$ и $x=-{\tfrac {a^{2}}{c}}$соответственно принадлежат парам полюса и поляра. Потому что они являются четными парами полюсов относительно окружности. $x^{2}+y^{2}=a^{2}$, направляющие можно построить с помощью циркуля и линейки (см. Обратная геометрия ).

Полюсно-полярные отношения существуют также для гипербол и парабол.

Свойства метрики

Все метрические свойства, приведенные ниже, относятся к эллипсу с уравнением

$${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$$

( 1 )

за исключением участка на площади, ограниченной наклонным эллипсом, где обобщенный вид уравнения ( 1 будет задан ).

Площадь

Район ​ $A_{\text{ellipse}}$ заключенный в эллипс:

$$A_{\text{ellipse}}=\pi ab$$

( 2 )

где $a$ и $b$ – длины большой и малой полуосей соответственно. Формула площади $\pi ab$ интуитивно понятно: начните с круга радиуса $b$ (так что его площадь $\pi b^{2}$) и растянуть его в раз $a/b$ сделать эллипс. Это масштабирует площадь на тот же коэффициент: $\pi b^{2}(a/b)=\pi ab.$ Однако использовать тот же подход для длины окружности было бы ошибочно – сравните интегралы ${\textstyle \int f(x)\,dx}$ и ${\textstyle \int {\sqrt {1+f'^{2}(x)}}\,dx}$. Строго доказать формулу площади с помощью интегрирования также легко следующим образом. Уравнение ( 1 ) можно переписать как ${\textstyle y(x)=b{\sqrt {1-x^{2}/a^{2}}}.}$ Для $x\in [-a,a],$ эта кривая представляет собой верхнюю половину эллипса. Значит, удвоенный интеграл $y(x)$ за интервал $[-a,a]$ будет площадь эллипса:

$${\begin{aligned}A_{\text{ellipse}}&=\int _{-a}^{a}2b{\sqrt {1-{\frac {x^{2}}{a^{2}}}}}\,dx\\&={\frac {b}{a}}\int _{-a}^{a}2{\sqrt {a^{2}-x^{2}}}\,dx.\end{aligned}}$$

Второй интеграл — это площадь круга радиуса $a,$ то есть, $\pi a^{2}.$ Так

$$A_{\text{ellipse}}={\frac {b}{a}}\pi a^{2}=\pi ab.$$

Эллипс, определенный неявно формулой $Ax^{2}+Bxy+Cy^{2}=1$ имеет площадь $2\pi /{\sqrt {4AC-B^{2}}}.$

Площадь также можно выразить через эксцентриситет и длину большой полуоси как $a^{2}\pi {\sqrt {1-e^{2}}}$ (получено путем решения задачи сглаживания с последующим вычислением малой полуоси).

Площадь, ограниченная наклонным эллипсом, равна $\pi \;y_{\text{int}}\,x_{\text{max}}$.

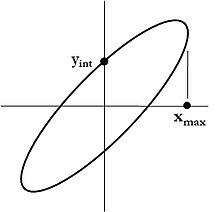
До сих пор мы имели дело с прямыми эллипсами, большая и малая оси которых параллельны $x$ и $y$ топоры. Однако в некоторых приложениях требуются наклонные эллипсы. Например, в оптике пучка заряженных частиц замкнутая область прямого или наклонного эллипса является важным свойством пучка, его эмиттансом . В этом случае по-прежнему применима простая формула, а именно:

$$A_{\text{ellipse}}=\pi \;y_{\text{int}}\,x_{\text{max}}=\pi \;x_{\text{int}}\,y_{\text{max}}$$

( 3 )

где $y_{\text{int}}$, $x_{\text{int}}$ являются перехватами и $x_{\text{max}}$, $y_{\text{max}}$ являются максимальными значениями. Это следует непосредственно из теоремы Аполлония .

Окружность

Дополнительная информация: Четверть меридиана.

Эллипсы одинаковой длины

Окружность $C$ эллипса это:

$$C\,=\,4a\int _{0}^{\pi /2}{\sqrt {1-e^{2}\sin ^{2}\theta }}\ d\theta \,=\,4a\,E(e)$$

где снова $a$ - длина большой полуоси, ${\textstyle e={\sqrt {1-b^{2}/a^{2}}}}$ – эксцентриситет, а функция $E$ – полный эллиптический интеграл второго рода ,

$$E(e)\,=\,\int _{0}^{\pi /2}{\sqrt {1-e^{2}\sin ^{2}\theta }}\ d\theta$$

что вообще-то не является элементарной функцией .

Окружность эллипса можно оценить с точки зрения $E(e)$ используя среднее арифметико-геометрическое Гаусса ; это квадратично сходящийся итерационный метод ( см. здесь подробности ).

Точный бесконечный ряд :

$${\begin{aligned}C&=2\pi a\left[{1-\left({\frac {1}{2}}\right)^{2}e^{2}-\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}{\frac {e^{4}}{3}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right)^{2}{\frac {e^{6}}{5}}-\cdots }\right]\\&=2\pi a\left[1-\sum _{n=1}^{\infty }\left({\frac {(2n-1)!!}{(2n)!!}}\right)^{2}{\frac {e^{2n}}{2n-1}}\right]\\&=-2\pi a\sum _{n=0}^{\infty }\left({\frac {(2n-1)!!}{(2n)!!}}\right)^{2}{\frac {e^{2n}}{2n-1}},\end{aligned}}$$

где $n!!$ - двойной факториал (расширенный до отрицательных нечетных целых чисел с помощью рекуррентного соотношения $(2n-1)!!=(2n+1)!!/(2n+1)$, для $n\leq 0$). Этот ряд сходится, но расширяясь по $h=(a-b)^{2}/(a+b)^{2},$ Джеймс Айвори и Бессель вывел выражение, которое сходится гораздо быстрее:

$${\begin{aligned}C&=\pi (a+b)\sum _{n=0}^{\infty }\left({\frac {(2n-3)!!}{2^{n}n!}}\right)^{2}h^{n}\\&=\pi (a+b)\left[1+{\frac {h}{4}}+\sum _{n=2}^{\infty }\left({\frac {(2n-3)!!}{2^{n}n!}}\right)^{2}h^{n}\right]\\&=\pi (a+b)\left[1+\sum _{n=1}^{\infty }\left({\frac {(2n-1)!!}{2^{n}n!}}\right)^{2}{\frac {h^{n}}{(2n-1)^{2}}}\right].\end{aligned}}$$

Шриниваса Рамануджан дал два близких приближения длины окружности в §16 книги «Модульные уравнения и приближения к окружности». $\pi$"; они есть

$$C\approx \pi {\biggl [}3(a+b)-{\sqrt {(3a+b)(a+3b)}}{\biggr ]}=\pi {\biggl [}3(a+b)-{\sqrt {10ab+3\left(a^{2}+b^{2}\right)}}{\biggr ]}$$

и

$$C\approx \pi \left(a+b\right)\left(1+{\frac {3h}{10+{\sqrt {4-3h}}}}\right),$$

где $h$ принимает тот же смысл, что и выше. Погрешности этих приближений, полученных эмпирическим путем, имеют порядок $h^{3}$ и $h^{5},$ соответственно.

Длина дуги

Дополнительная информация: Дуга меридиана § Расчет.

В более общем смысле, длина дуги части окружности как функция стягиваемого угла (или x координат любых двух точек в верхней половине эллипса) определяется неполным эллиптическим интегралом . Верхняя половина эллипса параметризуется

$$y=b\ {\sqrt {1-{\frac {x^{2}}{a^{2}}}\ }}~.$$

Тогда длина дуги $s$ от $\ x_{1}\$ к $\ x_{2}\$ является:

$$s=-b\int _{\arccos {\frac {x_{1}}{a}}}^{\arccos {\frac {x_{2}}{a}}}{\sqrt {\ 1+\left({\tfrac {a^{2}}{b^{2}}}-1\right)\ \sin ^{2}z~}}\;dz~.$$

Это эквивалентно

$$s=b\ \left[\;E\left(z\;{\Biggl |}\;1-{\frac {a^{2}}{b^{2}}}\right)\;\right]_{z\ =\ \arccos {\frac {x_{2}}{a}}}^{\arccos {\frac {x_{1}}{a}}}$$

где $E(z\mid m)$ – неполный эллиптический интеграл второго рода с параметром $m=k^{2}.$

Некоторые нижние и верхние оценки длины окружности канонического эллипса $\ x^{2}/a^{2}+y^{2}/b^{2}=1\$ с $\ a\geq b\$ являются

$${\begin{aligned}2\pi b&\leq C\leq 2\pi a\ ,\\\pi (a+b)&\leq C\leq 4(a+b)\ ,\\4{\sqrt {a^{2}+b^{2}\ }}&\leq C\leq {\sqrt {2\ }}\pi {\sqrt {a^{2}+b^{2}\ }}~.\end{aligned}}$$

Здесь верхняя граница $\ 2\pi a\$ - это длина описанной концентрической окружности, проходящей через конечные точки большой оси эллипса, а нижняя граница $4{\sqrt {a^{2}+b^{2}}}$ — периметр вписанного ромба с вершинами на концах большой и малой осей.

Кривизна

Кривизна выражением определяется $\kappa ={\frac {1}{a^{2}b^{2}}}\left({\frac {x^{2}}{a^{4}}}+{\frac {y^{2}}{b^{4}}}\right)^{-{\frac {3}{2}}}\ ,$ радиус кривизны в точке $(x,y)$:

$$\rho =a^{2}b^{2}\left({\frac {x^{2}}{a^{4}}}+{\frac {y^{2}}{b^{4}}}\right)^{\frac {3}{2}}={\frac {1}{a^{4}b^{4}}}{\sqrt {\left(a^{4}y^{2}+b^{4}x^{2}\right)^{3}}}\ .$$

Радиус кривизны в двух вершинах $(\pm a,0)$ и центры кривизны:

$$\rho _{0}={\frac {b^{2}}{a}}=p\ ,\qquad \left(\pm {\frac {c^{2}}{a}}\,{\bigg |}\,0\right)\ .$$

Радиус кривизны в двух ко-вершинах $(0,\pm b)$ и центры кривизны:

$$\rho _{1}={\frac {a^{2}}{b}}\ ,\qquad \left(0\,{\bigg |}\,\pm {\frac {c^{2}}{b}}\right)\ .$$

В геометрии треугольника

Эллипсы появляются в геометрии треугольника как

1. Эллипс Штейнера : эллипс, проходящий через вершины треугольника с центром в центроиде,
2. эллипсы : эллипсы, которые касаются сторон треугольника. Особыми случаями являются эллипс Штейнера и эллипс Мандарта .

Как плоские сечения квадрик

Эллипсы представляют собой плоские сечения следующих квадрик :

• Эллипсоид
• Эллиптический конус
• Эллиптический цилиндр
• Гиперболоид одного листа
• Гиперболоид из двух листов

• 
  Эллипсоид
• 
  Эллиптический конус
• 
  Эллиптический цилиндр
• 
  Гиперболоид одного листа
• 
  Гиперболоид из двух листов

Приложения

Физика

и

См. Также: зона Френеля

Волновая картина маленькой капли, упавшей в ртуть в фокусах эллипса.

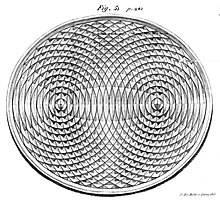
Если поверхность воды возмущена в одном фокусе эллиптического резервуара для воды, круговые волны этого возмущения после отражения от стенок сходятся одновременно в одной точке: втором фокусе . Это является следствием того, что общая длина перемещения одинакова на любом пути отскока от стены между двумя фокусами.

Аналогично, если источник света поместить в один фокус эллиптического зеркала , все световые лучи в плоскости эллипса отражаются во второй фокус. Поскольку ни одна другая гладкая кривая не обладает таким свойством, ее можно использовать как альтернативное определение эллипса. (В частном случае круга с источником в центре весь свет будет отражаться обратно в центр.) Если эллипс вращается вдоль своей большой оси, образуя эллипсоидное зеркало (в частности, вытянутый сфероид ), это свойство сохраняется. для всех лучей, исходящих из источника. В качестве альтернативы можно использовать цилиндрическое зеркало с эллиптическим поперечным сечением для фокусировки света линейной люминесцентной лампы вдоль линии бумаги; такие зеркала используются в некоторых сканерах документов .

Звуковые волны отражаются аналогичным образом, поэтому в большом эллиптическом помещении человек, стоящий в одном фокусе, прекрасно слышит человека, стоящего в другом фокусе. Эффект еще более заметен под сводчатой ​​крышей в форме части вытянутого сфероида. Такая комната называется камерой шепота . Тот же эффект можно продемонстрировать с помощью двух отражателей, имеющих форму торцевых крышек такого сфероида, расположенных друг против друга на нужном расстоянии. Примерами могут служить Национальный зал скульптур в Капитолии США (где, как говорят, Джон Куинси Адамс использовал это помещение для подслушивания политических вопросов); Скиния мормонов на Храмовой площади в Солт-Лейк-Сити , штат Юта ; на выставке звука в Музее науки и промышленности в Чикаго ; перед Университетом Иллинойса в аудитории Урбана-Шампейн Феллингер; а также в боковой камере дворца Карла V в Альгамбре .

Планетарные орбиты

Основная статья: Эллиптическая орбита

В 17 веке Иоганн Кеплер обнаружил, что орбиты, по которым планеты движутся вокруг Солнца, представляют собой эллипсы с Солнцем [приблизительно] в одном фокусе в своем первом законе движения планет . Позже Исаак Ньютон объяснил это как следствие своего закона всемирного тяготения .

В более общем смысле, в гравитационной задаче двух тел , если два тела связаны друг с другом (то есть общая энергия отрицательна), их орбиты представляют собой подобные эллипсы с общим барицентром, являющимся одним из фокусов каждого эллипса. Другой фокус любого эллипса не имеет известного физического значения. Орбита любого тела в системе отсчета другого также представляет собой эллипс, причем другое тело находится в том же фокусе.

Кеплеровы эллиптические орбиты являются результатом любой радиально направленной силы притяжения, сила которой обратно пропорциональна квадрату расстояния. Таким образом, в принципе движение двух противоположно заряженных частиц в пустом пространстве также было бы эллипсом. (Однако этот вывод игнорирует потери из-за электромагнитного излучения и квантовых эффектов , которые становятся существенными, когда частицы движутся с высокой скоростью.)

Для эллиптических орбит полезные соотношения, включающие эксцентриситет $e$ являются:

$${\begin{aligned}e&={\frac {r_{a}-r_{p}}{r_{a}+r_{p}}}={\frac {r_{a}-r_{p}}{2a}}\\r_{a}&=(1+e)a\\r_{p}&=(1-e)a\end{aligned}}$$

где

• $r_{a}$ — радиус в апоапсисе , т. е. самое дальнее расстояние орбиты до барицентра системы, который является фокусом эллипса
• $r_{p}$ это радиус в перицентре , ближайшее расстояние
• $a$ длина большой полуоси

Также с точки зрения $r_{a}$ и $r_{p}$, большая полуось $a$ — их среднее арифметическое , малая полуось $b$ — их среднее геометрическое , а полурасширенная прямая кишка $\ell$ является их гармоническим средним значением . Другими словами,

$${\begin{aligned}a&={\frac {r_{a}+r_{p}}{2}}\\[2pt]b&={\sqrt {r_{a}r_{p}}}\\[2pt]\ell &={\frac {2}{{\frac {1}{r_{a}}}+{\frac {1}{r_{p}}}}}={\frac {2r_{a}r_{p}}{r_{a}+r_{p}}}.\end{aligned}}$$

Гармонические осцилляторы

Общее решение для гармонического осциллятора в двух или более измерениях также представляет собой эллипс. Так обстоит дело, например, с длинным маятником, который может свободно двигаться в двух измерениях; массы, прикрепленной к неподвижной точке совершенно упругой пружиной ; или любого объекта, который движется под действием силы притяжения, прямо пропорциональной его расстоянию от неподвижного аттрактора. Однако в отличие от кеплеровских орбит эти «гармонические орбиты» имеют центр притяжения в геометрическом центре эллипса и имеют довольно простые уравнения движения.

Фазовая визуализация

В электронике относительную фазу двух синусоидальных сигналов можно сравнить, подав их на вертикальный и горизонтальный входы осциллографа . Если фигура Лиссажу представляет собой эллипс, а не прямую линию, два сигнала не совпадают по фазе.

Эллиптические шестерни

Две некруглые шестерни одинакового эллиптического контура, каждая из которых вращается вокруг одного фокуса и расположена под нужным углом, плавно вращаются, постоянно сохраняя контакт. В качестве альтернативы они могут быть соединены звеньевой цепью или ремнем ГРМ , а в случае велосипеда главная передняя звезда может быть эллиптической или овоидной , похожей на эллипс по форме. Такие эллиптические шестерни могут использоваться в механическом оборудовании для создания переменной угловой скорости или крутящего момента за счет постоянного вращения ведущей оси или, в случае велосипеда, для обеспечения изменяющейся скорости вращения кривошипа с обратно изменяющимся механическим преимуществом .

Эллиптические велосипедные шестерни облегчают соскальзывание цепи с шестерни при переключении передач.

Примером применения механизма может служить устройство, наматывающее нить на коническую шпульку машины прядильной . Шпульке придется наматывать быстрее, когда нить находится у вершины, чем когда она находится у основания.

Оптика

• В материале, который является оптически анизотропным ( двулучепреломляющим ), показатель преломления зависит от направления света. Зависимость можно описать индексным эллипсоидом . (Если материал оптически изотропен , этот эллипсоид представляет собой сферу.)
• В с ламповой накачкой для направления света от лампы накачки (соосной с одной эллиптической фокальной осью) на стержень активной среды (соосный со второй фокальной осью) использованы эллиптические отражатели цилиндрической формы. твердотельных лазерах
• В лазерно-плазменных источниках EUV- света, используемых в литографии микрочипов , EUV-свет генерируется плазмой, расположенной в первичном фокусе эллипсоидного зеркала, и собирается во вторичном фокусе на входе литографической машины.

Статистика и финансы

В статистике двумерный случайный вектор $(X,Y)$ распределена совместно эллиптически, если ее контуры изоплотности — места равных значений функции плотности — являются эллипсами. Эта концепция распространяется на произвольное количество элементов случайного вектора, и в этом случае, как правило, контуры изоплотности представляют собой эллипсоиды. Особым случаем является многомерное нормальное распределение . Эллиптические распределения важны в финансах, потому что, если нормы доходности активов совместно распределены эллиптически, тогда все портфели могут быть полностью охарактеризованы их средним значением и дисперсией, то есть любые два портфеля с одинаковым средним значением и дисперсией доходности портфеля имеют одинаковое распределение портфеля. возвращаться.

Компьютерная графика

Рисование эллипса как графического примитива часто встречается в стандартных библиотеках отображения, таких как MacIntosh QuickDraw API и Direct2D в Windows. Джек Брезенхем из IBM наиболее известен изобретением примитивов двумерного рисования, включая рисование линий и кругов, с использованием только быстрых целочисленных операций, таких как сложение и ветвление по биту переноса. MLV Pitteway расширил алгоритм Брезенхема для прямых до коник в 1967 году. Еще одно эффективное обобщение для рисования эллипсов было изобретено в 1984 году Джерри Ван Акеном.

В 1970 году Дэнни Коэн представил на конференции «Компьютерная графика 1970» в Англии линейный алгоритм рисования эллипсов и кругов. В 1971 году Л. Б. Смит опубликовал аналогичные алгоритмы для всех конических сечений и доказал их хорошие свойства. Этим алгоритмам требуется всего несколько умножений и сложений для вычисления каждого вектора.

В компьютерной графике выгодно использовать параметрическую формулировку, поскольку плотность точек наибольшая там, где имеется наибольшая кривизна. Таким образом, изменение наклона между каждой последующей точкой невелико, что уменьшает кажущуюся «неровность» аппроксимации.

Рисование с помощью путей Безье

Составные кривые Безье также можно использовать для рисования эллипса с достаточной точностью, поскольку любой эллипс можно рассматривать как аффинное преобразование круга. Сплайновые методы, используемые для рисования круга, могут использоваться для рисования эллипса, поскольку составляющие кривые Безье ведут себя соответствующим образом при таких преобразованиях.

Теория оптимизации

Иногда бывает полезно найти минимальный ограничивающий эллипс на множестве точек. Метод эллипсоида весьма полезен для решения этой проблемы.

См. также

• Декартов овал , обобщение эллипса.
• Циркумконический и неконический
• Расстояние наибольшего сближения эллипсов
• Эллипс фитинг
• Эллиптические координаты — ортогональная система координат, основанная на семействах эллипсов и гипербол.
• Эллиптическое уравнение в частных производных
• Эллиптическое распределение в статистике
• Эллиптический купол
• Геодезические на эллипсоиде
• Большой эллипс
• Законы движения планет Кеплера
• n -ellipse , обобщение эллипса для n фокусов
• Овал
• Сфероид — эллипсоид, полученный вращением эллипса вокруг его большой или малой оси.
• Стадион (геометрия) — двумерная геометрическая фигура, состоящая из прямоугольника с полукругами на двух противоположных сторонах.
• Окружность Штайнера — уникальный эллипс, описывающий треугольник и разделяющий его центроид.
• Суперэллипс , обобщение эллипса, которое может выглядеть более прямоугольным или более «заостренным».
• Истинная , эксцентричная и средняя аномалия

Ссылки

• Безант, WH (1907). «Глава III. Эллипс» . Конические сечения . Лондон: Джордж Белл и сыновья. п. 50.
• Коксетер, HSM (1969). Введение в геометрию (2-е изд.). Нью-Йорк: Уайли. стр. 115–9 .
• Месерв, Брюс Э. (1983) [1959], Фундаментальные концепции геометрии , Dover Publications, ISBN  978-0-486-63415-9
• Миллер, Чарльз Д.; Лиал, Маргарет Л.; Шнайдер, Дэвид И. (1990). Основы студенческой алгебры (3-е изд.). Скотт Форесман/Литтл. п. 381 . ISBN  978-0-673-38638-0 .
• Проттер, Мюррей Х.; Морри, Чарльз Б. младший (1970), Колледжское исчисление с аналитической геометрией (2-е изд.), Чтение: Аддисон-Уэсли , LCCN   76087042

Внешние ссылки

• Цитаты, связанные с эллипсом, в Wikiquote
• СМИ, связанные с эллипсами, на Викискладе?
• эллипс в PlanetMath .
• Вайсштейн, Эрик В. «Эллипс» . Математический мир .
• Вайсштейн, Эрик В. «Эллипс как частный случай гипотрохоиды» . Математический мир .
• Вывод Аполлонием эллипса при сближении
• Форма и история эллипса в Вашингтоне, округ Колумбия, Кларк Кимберлинг
• Калькулятор окружности эллипса
• Коллекция анимированных демонстраций эллипсов
• Иванов, А.Б. (2001) [1994], «Эллипс» , Энциклопедия Математики , EMS Press
• Траммель по Франсу ван Скутену
• «Почему нет уравнения для периметра эллипса‽» на YouTube Мэтта Паркера.