Гипербола

Эта статья о геометрической кривой. О термине, используемом в риторике, см. «Гипербола» .

Гипербола — разомкнутая кривая с двумя ветвями, пересечение плоскости обеими половинами двойного конуса . Плоскость не обязательно должна быть параллельна оси конуса; гипербола в любом случае будет симметричной.

Гипербола (красная): особенности

В математике гипербола ​ ( / h aɪ ˈ p ɜːr b ə l ə / ; пл. гиперболы или гиперболы /- l iː / ; прил. гиперболический / ˌ h aɪ p ər ˈ b ɒ l ɪ k / ) — это тип гладкой кривой, лежащей в плоскости , определяемый ее геометрическими свойствами или уравнениями , для которых она является множеством решений. Гипербола состоит из двух частей, называемых связными компонентами или ветвями, которые являются зеркальными отражениями друг друга и напоминают два бесконечных лука . Гипербола — один из трёх видов конического сечения , образованный пересечением плоскости и двойного конуса . (Другие конические сечения — парабола и эллипс . Окружность — частный случай эллипса.) Если плоскость пересекает обе половины двойного конуса, но не проходит через вершину конусов, то коника — это гипербола. .

Помимо того, что гипербола является коническим сечением, она может возникнуть как геометрическое место точек, разность расстояний до двух фиксированных фокусов которых постоянна, как кривая, для каждой точки которой лучи, ведущие к двум фиксированным фокусам, отражаются через касательную линию в этой точке. или как решение некоторых двумерных квадратных уравнений, таких как взаимности соотношение $xy=1.$ В практических приложениях гипербола может возникать как путь, по которому следует тень кончика солнечных часов , гномона форма открытой орбиты , например, у небесного объекта, превышающая скорость убегания ближайшего гравитационного тела, или траектория рассеяния субатомной частицы и другие.

Каждая ветвь гиперболы имеет два плеча, которые становятся более прямыми (меньшая кривизна) по мере удаления от центра гиперболы. Диагонально противоположные рукава, по одному от каждой ветви, в пределе стремятся к общей линии, называемой асимптотой этих двух плеч. Итак, существуют две асимптоты, пересечение которых находится в центре симметрии гиперболы, которую можно рассматривать как зеркальную точку, вокруг которой каждая ветвь отражается, образуя другую ветвь. В случае кривой $y(x)=1/x$ асимптоты представляют собой две оси координат .

Гиперболы разделяют многие аналитические свойства эллипсов, такие как эксцентриситет , фокус и директриса . Обычно переписка может осуществляться не более чем с помощью смены знака в каком-то периоде. Многие другие математические объекты берут свое начало от гиперболы, например, гиперболические параболоиды (седловые поверхности), гиперболоиды («мусорные корзины»), гиперболическая геометрия ( Лобачевского знаменитая неевклидова геометрия ), гиперболические функции (sinh, cosh, tanh и т. д.). .) и гировекторные пространства (геометрия, предложенная для использования как в теории относительности , так и в квантовой механике , которая не является евклидовой ).

Этимология и история

Слово «гипербола» происходит от греческого ὑπερβολή , что означает «свергнутый» или «чрезмерный», от которого также происходит английский термин «гипербола» . Гиперболы были открыты Менехмом при исследовании проблемы удвоения куба , но назывались тогда сечениями тупых конусов. Считается, что термин «гипербола» был придуман Аполлонием Пергским ( ок. 262 – ок. 190 до н.э. ) в его окончательном труде о конических сечениях , «Кониках» . Названия двух других общих конических сечений, эллипса и параболы , происходят от соответствующих греческих слов, означающих «недостаток» и «применение»; все три названия заимствованы из более ранней пифагорейской терминологии, которая относилась к сравнению стороны прямоугольников фиксированной площади с заданным отрезком. Прямоугольник может быть «приложен» к сегменту (то есть иметь равную длину), быть короче сегмента или превышать его.

Определения

Как геометрическое положение точек

Гипербола: определение по расстояниям точек до двух неподвижных точек (фокусов).

Гипербола: определение с круговой направляющей

Гиперболу можно определить геометрически как набор точек ( место точек ) на евклидовой плоскости:

Гипербола – это множество точек, такое что для любой точки $P$ набора, абсолютная разница расстояний $|PF_{1}|,\,|PF_{2}|$ к двум фиксированным точкам $F_{1},F_{2}$ ( фокусы ) постоянна, обычно обозначается $2a,\,a>0$:

$$H=\left\{P:\left|\left|PF_{2}\right|-\left|PF_{1}\right|\right|=2a\right\}.$$

Середина $M$ Отрезок, соединяющий фокусы, называется центром гиперболы. Линия, проходящая через фокусы, называется большой осью . Он содержит вершины $V_{1},V_{2}$, которые имеют расстояние $a$ в центр. Расстояние $c$ фокусов к центру называется фокусным расстоянием или линейным эксцентриситетом . Частное ${\tfrac {c}{a}}$ это эксцентриситет $e$.

Уравнение $\left|\left|PF_{2}\right|-\left|PF_{1}\right|\right|=2a$ можно посмотреть по-другому (см. схему):
Если $c_{2}$ это круг со средней точкой $F_{2}$ и радиус $2a$, то расстояние до точки $P$ правой ветки к кругу $c_{2}$ равно расстоянию до фокуса $F_{1}$:

$$|PF_{1}|=|Pc_{2}|.$$

$c_{2}$ называется круговой директрисой (связанной с фокусом $F_{2}$) гиперболы. Чтобы получить левую ветвь гиперболы, нужно использовать круговую направляющую, связанную с $F_{1}$. Это свойство не следует путать с определением гиперболы с помощью направляющей (линии) ниже.

Гипербола с уравнением y = A / x

Вращение системы координат для описания прямоугольной гиперболы как графика функции.

Три прямоугольные гиперболы $y=A/x$ с осями координат как асимптотами
красный: А = 1; пурпурный: А = 4; синий: А = 9

Если xy система координат повернута вокруг начала координат на угол $+45^{\circ }$ и новые координаты $\xi ,\eta$ назначены, то $x={\tfrac {\xi +\eta }{\sqrt {2}}},\;y={\tfrac {-\xi +\eta }{\sqrt {2}}}$.
Прямоугольная гипербола ${\tfrac {x^{2}-y^{2}}{a^{2}}}=1$ (у которого полуоси равны) имеет новое уравнение ${\tfrac {2\xi \eta }{a^{2}}}=1$.Решение для $\eta$ урожайность $\eta ={\tfrac {a^{2}/2}{\xi }}\ .$

Таким образом, в системе координат xy график функции $f:x\mapsto {\tfrac {A}{x}},\;A>0\;,$ с уравнением

$$y={\frac {A}{x}}\;,A>0\;,$$

представляет собой прямоугольную гиперболу целиком в первом и третьем квадранте с

• оси координат как асимптоты ,
• линия $y=x$ как главная ось ,
• центр ​ $(0,0)$ и полуось $a=b={\sqrt {2A}}\;,$
• вершины ​ $\left({\sqrt {A}},{\sqrt {A}}\right),\left(-{\sqrt {A}},-{\sqrt {A}}\right)\;,$
• полурасширенная прямая кишка и радиус кривизны в вершинах $p=a={\sqrt {2A}}\;,$
• линейный эксцентриситет $c=2{\sqrt {A}}$ и эксцентриситет $e={\sqrt {2}}\;,$
• касательная ​ $y=-{\tfrac {A}{x_{0}^{2}}}x+2{\tfrac {A}{x_{0}}}$ в точку $(x_{0},A/x_{0})\;.$

Вращение исходной гиперболы на $-45^{\circ }$ приводит к прямоугольной гиперболе полностью во втором и четвертом квадрантах с теми же асимптотами, центром, полуширотной прямой кишкой, радиусом кривизны в вершинах, линейным эксцентриситетом и эксцентриситетом, что и в случае $+45^{\circ }$ вращение с уравнением

$$y=-{\frac {A}{x}}\;,~~A>0\;,$$

• полуоси ​ $a=b={\sqrt {2A}}\;,$
• линия $y=-x$ в качестве главной оси,
• вершины ​ $\left(-{\sqrt {A}},{\sqrt {A}}\right),\left({\sqrt {A}},-{\sqrt {A}}\right)\;.$

Смещение гиперболы с помощью уравнения $y={\frac {A}{x}},\ A\neq 0\ ,$ так что новый центр $(c_{0},d_{0})$, дает новое уравнение

$$y={\frac {A}{x-c_{0}}}+d_{0}\;,$$

и новые асимптоты $x=c_{0}$ и $y=d_{0}$. Параметры формы $a,b,p,c,e$ остаются неизменными.

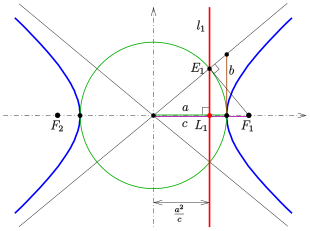
По свойству Directrix

Гипербола: свойство директрисы

Гипербола: определение со свойством направляющей

Две линии на расстоянии ${\textstyle d={\frac {a^{2}}{c}}}$ из центра и параллельно малой оси называются директрисами гиперболы (см. схему).

Для произвольной точки $P$ гиперболы частное расстояния до одного фокуса и соответствующей направляющей (см. схему) равно эксцентриситету:

$${\frac {|PF_{1}|}{|Pl_{1}|}}={\frac {|PF_{2}|}{|Pl_{2}|}}=e={\frac {c}{a}}\,.$$

Доказательство для пары $F_{1},l_{1}$ следует из того, что $|PF_{1}|^{2}=(x-c)^{2}+y^{2},\ |Pl_{1}|^{2}=\left(x-{\tfrac {a^{2}}{c}}\right)^{2}$ и $y^{2}={\tfrac {b^{2}}{a^{2}}}x^{2}-b^{2}$ удовлетворить уравнение

$$|PF_{1}|^{2}-{\frac {c^{2}}{a^{2}}}|Pl_{1}|^{2}=0\ .$$

Второй случай доказывается аналогично.

Карандаш из коник с общей вершиной и общей полуширокой прямой кишкой.

Обратное утверждение также верно и может использоваться для определения гиперболы (аналогично определению параболы):

Для любой точки $F$ (фокус), любая линия $l$ (директриса) не через $F$ и любое действительное число $e$ с $e>1$ множество точек (место точек), для которых частное расстояний до точки и до прямой равно $e$

$$H=\left\{P\,{\Biggr |}\,{\frac {|PF|}{|Pl|}}=e\right\}$$

является гиперболой.

(Выбор $e=1$ дает параболу , и если $e<1$ эллипс ) .

Доказательство

Позволять $F=(f,0),\ e>0$ и предположим $(0,0)$ является точкой на кривой.Директриса $l$ имеет уравнение $x=-{\tfrac {f}{e}}$. С $P=(x,y)$, отношение $|PF|^{2}=e^{2}|Pl|^{2}$ выдает уравнения

$(x-f)^{2}+y^{2}=e^{2}\left(x+{\tfrac {f}{e}}\right)^{2}=(ex+f)^{2}$ и $x^{2}(e^{2}-1)+2xf(1+e)-y^{2}=0.$

Замена $p=f(1+e)$ урожайность

$$x^{2}(e^{2}-1)+2px-y^{2}=0.$$

Это уравнение эллипса ( $e<1$) или парабола ( $e=1$) или гипербола ( $e>1$). Все эти невырожденные коники имеют общее начало в виде вершины (см. диаграмму).

Если $e>1$, ввести новые параметры $a,b$ так что $e^{2}-1={\tfrac {b^{2}}{a^{2}}},{\text{ and }}\ p={\tfrac {b^{2}}{a}}$, и тогда приведенное выше уравнение принимает вид

$${\frac {(x+a)^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1\,,$$

которое представляет собой уравнение гиперболы с центром $(-a,0)$, ось X как главная ось и большая/малая полуось $a,b$.

Гипербола: построение директрисы

Построение директрисы

Из-за $c\cdot {\tfrac {a^{2}}{c}}=a^{2}$ точка $L_{1}$ директрисы $l_{1}$ (см. схему) и сфокусируйтесь $F_{1}$ обратны относительно инверсии окружности в окружности $x^{2}+y^{2}=a^{2}$ (на схеме зеленой). Следовательно, точка $E_{1}$ можно построить с помощью теоремы Фалеса (на схеме не показана). Директриса $l_{1}$ перпендикуляр к прямой ${\overline {F_{1}F_{2}}}$ сквозной пункт $E_{1}$.

Альтернативное строительство $E_{1}$: Расчет показывает, что эта точка $E_{1}$ есть пересечение асимптоты с ее перпендикуляром через $F_{1}$ (см. схему).

Как плоское сечение конуса

Гипербола (красная): два вида конуса и две сферы Одуванчика d ₁ , d ₂

Пересечение вертикального двойного конуса плоскостью, не проходящей через вершину, с наклоном, большим, чем наклон прямых на конусе, является гиперболой (см. рисунок: красная кривая). Чтобы доказать определяющее свойство гиперболы (см. выше), используются две сферы Одуванчика. $d_{1},d_{2}$, представляющие собой сферы, соприкасающиеся с конусом по окружностям $c_{1}$, $c_{2}$ и пересекающая (гипербола) плоскость в точках $F_{1}$ и $F_{2}$. Оказывается: $F_{1},F_{2}$ являются фокусами гиперболы.

1. Позволять $P$ — произвольная точка кривой пересечения.
2. Образующая содержащая конуса, $P$ пересекает круг $c_{1}$ в точку $A$ и круг $c_{2}$ в какой-то момент $B$.
3. Линейные сегменты ${\overline {PF_{1}}}$ и ${\overline {PA}}$ касательны к сфере $d_{1}$ и, следовательно, имеют одинаковую длину.
4. Линейные сегменты ${\overline {PF_{2}}}$ и ${\overline {PB}}$ касательны к сфере $d_{2}$ и, следовательно, имеют одинаковую длину.
5. Результат: $|PF_{1}|-|PF_{2}|=|PA|-|PB|=|AB|$ не зависит от точки гиперболы $P$, потому что неважно, где точка $P$ является, $A,B$ должен быть в кругах $c_{1}$, $c_{2}$, и отрезок прямой $AB$ должен пересечь вершину. Поэтому, как точка $P$ движется по красной кривой (гиперболе), отрезок ${\overline {AB}}$ просто вращается вокруг вершины, не меняя своей длины.

Конструкция булавки и струны

Гипербола: конструкция штифта и струны

Определение гиперболы по ее фокусам и круговым направляющим (см. выше) можно использовать для построения ее дуги с помощью булавок, веревки и линейки:

0. Выберите фокусы $F_{1},F_{2}$, вершины $V_{1},V_{2}$ и одна из круговых направляющих , например $c_{2}$ (круг радиусом $2a$)
1. Линейка точке закреплена в $F_{2}$ свободно вращаться вокруг $F_{2}$. Точка $B$ отмечается на расстоянии $2a$.
2. Строка ​ длиной $|AB|$ готово.
3. Один конец веревки закреплен в точке $A$ на линейке другой конец прикреплен к точке $F_{1}$.
4. Возьмите ручку и крепко прижмите веревку к краю линейки.
5. Вращение линейки вокруг $F_{2}$ побуждает перо нарисовать дугу правой ветви гиперболы, поскольку $|PF_{1}|=|PB|$ (см. определение гиперболы круговыми направляющими ).

гиперболы

Гипербола: поколение Штейнера

Гипербола y = 1/ x : поколение Штейнера

Следующий метод построения отдельных точек гиперболы основан на порождении Штейнера невырожденного конического сечения :

Даны два карандаша $B(U),B(V)$ линий в двух точках $U,V$ (все строки, содержащие $U$ и $V$соответственно) и проективное, но не перспективное отображение $\pi$ из $B(U)$ на $B(V)$, то точки пересечения соответствующих прямых образуют невырожденное проективное коническое сечение.

Для генерации точек гиперболы ${\tfrac {x^{2}}{a^{2}}}-{\tfrac {y^{2}}{b^{2}}}=1$ каждый использует карандаши в вершинах $V_{1},V_{2}$. Позволять $P=(x_{0},y_{0})$ быть точкой гиперболы и $A=(a,y_{0}),B=(x_{0},0)$. Отрезок линии ${\overline {BP}}$ разделен на n равноотстоящих друг от друга сегментов, и это деление проецируется параллельно диагонали $AB$ как направление на отрезок прямой ${\overline {AP}}$ (см. схему). Параллельная проекция является частью проективного отображения между пучками в точке $V_{1}$ и $V_{2}$ нужный. Точки пересечения любых двух связанных линий $S_{1}A_{i}$ и $S_{2}B_{i}$ являются точками однозначно определенной гиперболы.

Примечания:

• Подразделение может быть расширено за пределы точек $A$ и $B$ чтобы получить больше очков, но определение точек пересечения станет более неточным. Лучшая идея — расширить уже построенные точки с помощью симметрии (см. анимацию).
• Поколение Штейнера существует также для эллипсов и парабол.
• Генерацию Штейнера иногда называют методом параллелограмма, потому что вместо вершин можно использовать другие точки, которые начинаются с параллелограмма вместо прямоугольника.

Вписанные углы для гипербол y = a /( x − b ) + c и трехточечная форма

Гипербола: теорема о вписанном угле

Гипербола с уравнением $y={\tfrac {a}{x-b}}+c,\ a\neq 0$ однозначно определяется тремя точками $(x_{1},y_{1}),\;(x_{2},y_{2}),\;(x_{3},y_{3})$ с разными координатами x и y . Простой способ определения параметров формы $a,b,c$ использует теорему о вписанном угле для гипербол:

Чтобы измерить угол между двумя линиями с помощью уравнений $y=m_{1}x+d_{1},\ y=m_{2}x+d_{2}\ ,m_{1},m_{2}\neq 0$ в этом контексте используется частное

$${\frac {m_{1}}{m_{2}}}\ .$$

Аналогично теореме о вписанном угле для окружностей получаем

Теорема о вписанном угле для гипербол — За четыре очка $P_{i}=(x_{i},y_{i}),\ i=1,2,3,4,\ x_{i}\neq x_{k},y_{i}\neq y_{k},i\neq k$ (см. диаграмму) верно следующее утверждение:

Четыре точки находятся на гиперболе с уравнением $y={\tfrac {a}{x-b}}+c$ тогда и только тогда, когда углы при $P_{3}$ и $P_{4}$ равны в смысле измерения, приведенного выше. Это означает, что если

$${\frac {(y_{4}-y_{1})}{(x_{4}-x_{1})}}{\frac {(x_{4}-x_{2})}{(y_{4}-y_{2})}}={\frac {(y_{3}-y_{1})}{(x_{3}-x_{1})}}{\frac {(x_{3}-x_{2})}{(y_{3}-y_{2})}}$$

Доказательство можно получить прямым расчетом. Если точки находятся на гиперболе, можно предположить, что уравнение гиперболы имеет вид $y=a/x$.

Следствием теоремы о вписанном угле для гипербол является

Трехточечная форма уравнения гиперболы — уравнение гиперболы, определяемое тремя точками. $P_{i}=(x_{i},y_{i}),\ i=1,2,3,\ x_{i}\neq x_{k},y_{i}\neq y_{k},i\neq k$ является решением уравнения

$${\frac {({\color {red}y}-y_{1})}{({\color {green}x}-x_{1})}}{\frac {({\color {green}x}-x_{2})}{({\color {red}y}-y_{2})}}={\frac {(y_{3}-y_{1})}{(x_{3}-x_{1})}}{\frac {(x_{3}-x_{2})}{(y_{3}-y_{2})}}$$

для ${\color {red}y}$.

Как аффинный образ единичной гиперболы x ² − и ² = 1

Гипербола как аффинный образ единичной гиперболы

Другое определение гиперболы использует аффинные преобразования :

Любая гипербола является аффинным образом единичной гиперболы с уравнением $x^{2}-y^{2}=1$.

Параметрическое представление

Аффинное преобразование евклидовой плоскости имеет вид ${\vec {x}}\to {\vec {f}}_{0}+A{\vec {x}}$, где $A$ является регулярной матрицей (ее определитель не равен 0) и ${\vec {f}}_{0}$ — произвольный вектор. Если ${\vec {f}}_{1},{\vec {f}}_{2}$ – векторы-столбцы матрицы $A$, единичная гипербола $(\pm \cosh(t),\sinh(t)),t\in \mathbb {R} ,$ отображается на гиперболе

$${\vec {x}}={\vec {p}}(t)={\vec {f}}_{0}\pm {\vec {f}}_{1}\cosh t+{\vec {f}}_{2}\sinh t\ .$$

${\vec {f}}_{0}$ это центр, ${\vec {f}}_{0}+{\vec {f}}_{1}$ точка гиперболы и ${\vec {f}}_{2}$ касательный вектор в этой точке.

Вершины

В целом векторы ${\vec {f}}_{1},{\vec {f}}_{2}$ не перпендикулярны. Это означает, что в целом ${\vec {f}}_{0}\pm {\vec {f}}_{1}$ являются не вершинами гиперболы. Но ${\vec {f}}_{1}\pm {\vec {f}}_{2}$ укажите направления асимптот. Касательный вектор в точке ${\vec {p}}(t)$ является

$${\vec {p}}'(t)={\vec {f}}_{1}\sinh t+{\vec {f}}_{2}\cosh t\ .$$

Поскольку в вершине касательная перпендикулярна большой оси гиперболы, получается параметр $t_{0}$ вершины из уравнения

$${\vec {p}}'(t)\cdot \left({\vec {p}}(t)-{\vec {f}}_{0}\right)=\left({\vec {f}}_{1}\sinh t+{\vec {f}}_{2}\cosh t\right)\cdot \left({\vec {f}}_{1}\cosh t+{\vec {f}}_{2}\sinh t\right)=0$$

и, следовательно, от

$$\coth(2t_{0})=-{\tfrac {{\vec {f}}_{1}^{\,2}+{\vec {f}}_{2}^{\,2}}{2{\vec {f}}_{1}\cdot {\vec {f}}_{2}}}\ ,$$

что дает

$$t_{0}={\tfrac {1}{4}}\ln {\tfrac {\left({\vec {f}}_{1}-{\vec {f}}_{2}\right)^{2}}{\left({\vec {f}}_{1}+{\vec {f}}_{2}\right)^{2}}}.$$

Формулы $\cosh ^{2}x+\sinh ^{2}x=\cosh 2x$, $2\sinh x\cosh x=\sinh 2x$, и $\operatorname {arcoth} x={\tfrac {1}{2}}\ln {\tfrac {x+1}{x-1}}$ были использованы.

Две вершины гиперболы ${\vec {f}}_{0}\pm \left({\vec {f}}_{1}\cosh t_{0}+{\vec {f}}_{2}\sinh t_{0}\right).$

Неявное представление

Решение параметрического представления для $\cosh t,\sinh t$ по правилу Крамера и используя $\;\cosh ^{2}t-\sinh ^{2}t-1=0\;$, получаем неявное представление

$$\det \left({\vec {x}}\!-\!{\vec {f}}\!_{0},{\vec {f}}\!_{2}\right)^{2}-\det \left({\vec {f}}\!_{1},{\vec {x}}\!-\!{\vec {f}}\!_{0}\right)^{2}-\det \left({\vec {f}}\!_{1},{\vec {f}}\!_{2}\right)^{2}=0.$$

Гипербола в космосе

Определение гиперболы в этом разделе дает параметрическое представление произвольной гиперболы даже в пространстве, если допускается ${\vec {f}}\!_{0},{\vec {f}}\!_{1},{\vec {f}}\!_{2}$ быть векторами в пространстве.

Как аффинное изображение гиперболы y = 1/ x

Гипербола как аффинный образ y = 1/ x

Поскольку единичная гипербола $x^{2}-y^{2}=1$ аффинно эквивалентна гиперболе $y=1/x$произвольную гиперболу можно рассматривать как аффинный образ (см. предыдущий раздел) гиперболы $y=1/x\,$:

$${\vec {x}}={\vec {p}}(t)={\vec {f}}_{0}+{\vec {f}}_{1}t+{\vec {f}}_{2}{\tfrac {1}{t}},\quad t\neq 0\,.$$

$M:{\vec {f}}_{0}$ – центр гиперболы, векторы ${\vec {f}}_{1},{\vec {f}}_{2}$ имеют направления асимптот и ${\vec {f}}_{1}+{\vec {f}}_{2}$ является точкой гиперболы. Касательный вектор

$${\vec {p}}'(t)={\vec {f}}_{1}-{\vec {f}}_{2}{\tfrac {1}{t^{2}}}.$$

В вершине касательная перпендикулярна большой оси. Следовательно

$${\vec {p}}'(t)\cdot \left({\vec {p}}(t)-{\vec {f}}_{0}\right)=\left({\vec {f}}_{1}-{\vec {f}}_{2}{\tfrac {1}{t^{2}}}\right)\cdot \left({\vec {f}}_{1}t+{\vec {f}}_{2}{\tfrac {1}{t}}\right)={\vec {f}}_{1}^{2}t-{\vec {f}}_{2}^{2}{\tfrac {1}{t^{3}}}=0$$

а параметр вершины равен

$$t_{0}=\pm {\sqrt[{4}]{\frac {{\vec {f}}_{2}^{2}}{{\vec {f}}_{1}^{2}}}}.$$

$\left|{\vec {f}}\!_{1}\right|=\left|{\vec {f}}\!_{2}\right|$ эквивалентно $t_{0}=\pm 1$ и ${\vec {f}}_{0}\pm ({\vec {f}}_{1}+{\vec {f}}_{2})$ являются вершинами гиперболы.

Следующие свойства гиперболы легко доказываются с использованием представления гиперболы, введенного в этом разделе.

Касательная конструкция

асимптоты и P → касательная Конструкция касательной: заданы

Касательный вектор можно переписать путем факторизации:

$${\vec {p}}'(t)={\tfrac {1}{t}}\left({\vec {f}}_{1}t-{\vec {f}}_{2}{\tfrac {1}{t}}\right)\ .$$

Это означает, что

диагональ $AB$ параллелограмма $M:\ {\vec {f}}_{0},\ A={\vec {f}}_{0}+{\vec {f}}_{1}t,\ B:\ {\vec {f}}_{0}+{\vec {f}}_{2}{\tfrac {1}{t}},\ P:\ {\vec {f}}_{0}+{\vec {f}}_{1}t+{\vec {f}}_{2}{\tfrac {1}{t}}$ параллельна касательной в точке гиперболы $P$ (см. схему).

Это свойство позволяет построить касательную в точке гиперболы.

Это свойство гиперболы является аффинной версией 3-точечного вырождения теоремы Паскаля .

Площадь серого параллелограмма

Площадь серого параллелограмма $MAPB$ на диаграмме выше это

$${\text{Area}}=\left|\det \left(t{\vec {f}}_{1},{\tfrac {1}{t}}{\vec {f}}_{2}\right)\right|=\left|\det \left({\vec {f}}_{1},{\vec {f}}_{2}\right)\right|=\cdots ={\frac {a^{2}+b^{2}}{4}}$$

и, следовательно, не зависит от точки $P$. Последнее уравнение следует из расчета для случая, когда $P$ — вершина и гипербола в канонической форме ${\tfrac {x^{2}}{a^{2}}}-{\tfrac {y^{2}}{b^{2}}}=1\,.$

Построение точек

Построение точки: асимптоты и P ₁ заданы → P ₂

Для гиперболы с параметрическим представлением ${\vec {x}}={\vec {p}}(t)={\vec {f}}_{1}t+{\vec {f}}_{2}{\tfrac {1}{t}}$ (для простоты центр является началом координат) верно следующее:

Для любых двух точек $P_{1}:\ {\vec {f}}_{1}t_{1}+{\vec {f}}_{2}{\tfrac {1}{t_{1}}},\ P_{2}:\ {\vec {f}}_{1}t_{2}+{\vec {f}}_{2}{\tfrac {1}{t_{2}}}$ точки

$$A:\ {\vec {a}}={\vec {f}}_{1}t_{1}+{\vec {f}}_{2}{\tfrac {1}{t_{2}}},\ B:\ {\vec {b}}={\vec {f}}_{1}t_{2}+{\vec {f}}_{2}{\tfrac {1}{t_{1}}}$$

коллинеарны центру гиперболы (см. схему).

Простое доказательство является следствием уравнения ${\tfrac {1}{t_{1}}}{\vec {a}}={\tfrac {1}{t_{2}}}{\vec {b}}$.

Это свойство дает возможность построить точки гиперболы, если заданы асимптоты и одна точка.

Это свойство гиперболы является аффинной версией 4-точечного вырождения теоремы Паскаля .

Треугольник касательная-асимптоты

Гипербола: касательная-асимптоты-треугольник

Для простоты центр гиперболы может быть началом координат, а векторы ${\vec {f}}_{1},{\vec {f}}_{2}$ иметь одинаковую длину. Если последнее предположение не выполняется, можно сначала применить преобразование параметров (см. Выше), чтобы сделать предположение верным. Следовательно $\pm ({\vec {f}}_{1}+{\vec {f}}_{2})$ это вершины, $\pm ({\vec {f}}_{1}-{\vec {f}}_{2})$ охватываем малую ось и получаем $|{\vec {f}}_{1}+{\vec {f}}_{2}|=a$ и $|{\vec {f}}_{1}-{\vec {f}}_{2}|=b$.

Для точек пересечения касательной в точке ${\vec {p}}(t_{0})={\vec {f}}_{1}t_{0}+{\vec {f}}_{2}{\tfrac {1}{t_{0}}}$ с асимптотами получают очки

$$C=2t_{0}{\vec {f}}_{1},\ D={\tfrac {2}{t_{0}}}{\vec {f}}_{2}.$$

Площадь ​ треугольника $M,C,D$ можно вычислить с помощью определителя 2 × 2:

$$A={\tfrac {1}{2}}{\Big |}\det \left(2t_{0}{\vec {f}}_{1},{\tfrac {2}{t_{0}}}{\vec {f}}_{2}\right){\Big |}=2{\Big |}\det \left({\vec {f}}_{1},{\vec {f}}_{2}\right){\Big |}$$

(см. правила для определителей ). $\left|\det({\vec {f}}_{1},{\vec {f}}_{2})\right|$ площадь ромба, образованного ${\vec {f}}_{1},{\vec {f}}_{2}$. Площадь ромба равна половине произведения его диагоналей. Диагонали – это полуоси. $a,b$ гиперболы. Следовательно:

Площадь ​ треугольника $MCD$ не зависит от точки гиперболы: $A=ab.$

Возвратное движение круга

Возвратно -поступательное движение круга B C по кругу всегда дает коническое сечение , такое как гипербола. Процесс «возвратно-поступательного движения по кругу С » состоит в замене каждой линии и точки геометрической фигуры соответствующими полюсом и полярой соответственно. Полюс C линии — это инверсия ее ближайшей точки к окружности C , тогда как поляра точки — наоборот, а именно линия, ближайшая точка которой к является инверсией точки.

Эксцентриситет конического сечения, полученного возвратно-поступательным движением, представляет собой отношение расстояний между центрами двух окружностей к радиусу r круга возвратно-поступательного движения C . Если B и C представляют собой точки в центрах соответствующих окружностей, то

$$e={\frac {\overline {BC}}{r}}.$$

Поскольку эксцентриситет гиперболы всегда больше единицы, центр B должен лежать вне возвратно-поступательной C. окружности

что гипербола является одновременно местом расположения полюсов касательных линий к окружности B , а также огибающей полярных линий точек на B. Из этого определения следует , И наоборот, окружность B является огибающей поляр точек гиперболы и местом расположения полюсов касательных к гиперболе. Две касательные линии к B не имеют (конечных) полюсов, поскольку они проходят через центр C круга возвратно-поступательного движения C ; поляры соответствующих точек касания на B являются асимптотами гиперболы. Две ветви гиперболы соответствуют двум частям окружности B , разделенным этими точками касания.

Квадратное уравнение

Гиперболу также можно определить как уравнение второй степени в декартовых координатах. $(x,y)$ в самолете ,

$$A_{xx}x^{2}+2A_{xy}xy+A_{yy}y^{2}+2B_{x}x+2B_{y}y+C=0,$$

при условии, что константы $A_{xx},$ $A_{xy},$ $A_{yy},$ $B_{x},$ $B_{y},$ и $C$ удовлетворять определяющему условию

$$D:={\begin{vmatrix}A_{xx}&A_{xy}\\A_{xy}&A_{yy}\end{vmatrix}}<0.$$

Этот определитель условно называют дискриминантом конического сечения.

Особый случай гиперболы — вырожденная гипербола, состоящая из двух пересекающихся прямых — возникает, когда другой определитель равен нулю:

$$\Delta :={\begin{vmatrix}A_{xx}&A_{xy}&B_{x}\\A_{xy}&A_{yy}&B_{y}\\B_{x}&B_{y}&C\end{vmatrix}}=0.$$

Этот определитель $\Delta$ иногда называют дискриминантом конического сечения.

Коэффициенты общего уравнения можно получить по известной большой полуоси. $a,$ малая полуось $b,$ координаты центра $(x_{\circ },y_{\circ })$, и угол поворота $\theta$ (угол между положительной горизонтальной осью и большой осью гиперболы) по формулам:

$${\begin{aligned}A_{xx}&=-a^{2}\sin ^{2}\theta +b^{2}\cos ^{2}\theta ,&B_{x}&=-A_{xx}x_{\circ }-A_{xy}y_{\circ },\\[1ex]A_{yy}&=-a^{2}\cos ^{2}\theta +b^{2}\sin ^{2}\theta ,&B_{y}&=-A_{xy}x_{\circ }-A_{yy}y_{\circ },\\[1ex]A_{xy}&=\left(a^{2}+b^{2}\right)\sin \theta \cos \theta ,&C&=A_{xx}x_{\circ }^{2}+2A_{xy}x_{\circ }y_{\circ }+A_{yy}y_{\circ }^{2}-a^{2}b^{2}.\end{aligned}}$$

Эти выражения можно вывести из канонического уравнения

$${\frac {X^{2}}{a^{2}}}-{\frac {Y^{2}}{b^{2}}}=1$$

путем перевода и вращения координат $(x,y)$:

$${\begin{alignedat}{2}X&={\phantom {+}}\left(x-x_{\circ }\right)\cos \theta &&+\left(y-y_{\circ }\right)\sin \theta ,\\Y&=-\left(x-x_{\circ }\right)\sin \theta &&+\left(y-y_{\circ }\right)\cos \theta .\end{alignedat}}$$

Учитывая приведенную выше общую параметризацию гиперболы в декартовых координатах, эксцентриситет можно найти по формуле в разделе Коническое сечение#Эксцентриситет через коэффициенты .

Центр $(x_{c},y_{c})$ гиперболы можно определить по формулам

$${\begin{aligned}x_{c}&=-{\frac {1}{D}}\,{\begin{vmatrix}B_{x}&A_{xy}\\B_{y}&A_{yy}\end{vmatrix}}\,,\\[1ex]y_{c}&=-{\frac {1}{D}}\,{\begin{vmatrix}A_{xx}&B_{x}\\A_{xy}&B_{y}\end{vmatrix}}\,.\end{aligned}}$$

Что касается новых координат, $\xi =x-x_{c}$ и $\eta =y-y_{c},$ определяющее уравнение гиперболы можно записать

$$A_{xx}\xi ^{2}+2A_{xy}\xi \eta +A_{yy}\eta ^{2}+{\frac {\Delta }{D}}=0.$$

Главные оси гиперболы составляют угол $\varphi$ с позитивом $x$-ось, которая определяется выражением

$$\tan(2\varphi )={\frac {2A_{xy}}{A_{xx}-A_{yy}}}.$$

Поворот осей координат так, чтобы $x$-ось совмещена с поперечной осью, что приводит уравнение к канонической форме

$${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1.$$

Большая и малая полуоси $a$ и $b$ определяются уравнениями

$${\begin{aligned}a^{2}&=-{\frac {\Delta }{\lambda _{1}D}}=-{\frac {\Delta }{\lambda _{1}^{2}\lambda _{2}}},\\[1ex]b^{2}&=-{\frac {\Delta }{\lambda _{2}D}}=-{\frac {\Delta }{\lambda _{1}\lambda _{2}^{2}}},\end{aligned}}$$

где $\lambda _{1}$ и $\lambda _{2}$ являются корнями квадратного уравнения

$$\lambda ^{2}-\left(A_{xx}+A_{yy}\right)\lambda +D=0.$$

Для сравнения соответствующее уравнение вырожденной гиперболы (состоящей из двух пересекающихся прямых) имеет вид

$${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=0.$$

Касательная линия к данной точке $(x_{0},y_{0})$ на гиперболе определяется уравнением

$$Ex+Fy+G=0$$

где $E,$ $F,$ и $G$ определяются

$${\begin{aligned}E&=A_{xx}x_{0}+A_{xy}y_{0}+B_{x},\\[1ex]F&=A_{xy}x_{0}+A_{yy}y_{0}+B_{y},\\[1ex]G&=B_{x}x_{0}+B_{y}y_{0}+C.\end{aligned}}$$

Нормаль к гиперболе в той же точке задается уравнением

$$F(x-x_{0})-E(y-y_{0})=0.$$

Нормальная линия перпендикулярна касательной, и обе проходят через одну и ту же точку. $(x_{0},y_{0}).$

Из уравнения

$${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1,\qquad 0<b\leq a,$$

левый фокус $(-ae,0)$ и правильный фокус $(ae,0),$ где $e$ это эксцентриситет. Обозначим расстояния от точки $(x,y)$ к левому и правому фокусу, как $r_{1}$ и $r_{2}.$ Для точки на правой ветви

$$r_{1}-r_{2}=2a,$$

и для точки на левой ветви,

$$r_{2}-r_{1}=2a.$$

Это можно доказать следующим образом:

Если $(x,y)$ — точка на гиперболе, расстояние до левой фокальной точки равно

$$r_{1}^{2}=(x+ae)^{2}+y^{2}=x^{2}+2xae+a^{2}e^{2}+\left(x^{2}-a^{2}\right)\left(e^{2}-1\right)=(ex+a)^{2}.$$

До правого фокуса расстояние равно

$$r_{2}^{2}=(x-ae)^{2}+y^{2}=x^{2}-2xae+a^{2}e^{2}+\left(x^{2}-a^{2}\right)\left(e^{2}-1\right)=(ex-a)^{2}.$$

Если $(x,y)$ является точкой на правой ветви гиперболы, тогда $ex>a$ и

$${\begin{aligned}r_{1}&=ex+a,\\r_{2}&=ex-a.\end{aligned}}$$

Вычитая эти уравнения, получаем

$$r_{1}-r_{2}=2a.$$

Если $(x,y)$ — точка на левой ветви гиперболы, тогда $ex<-a$ и

$${\begin{aligned}r_{1}&=-ex-a,\\r_{2}&=-ex+a.\end{aligned}}$$

Вычитая эти уравнения, получаем

$$r_{2}-r_{1}=2a.$$

В декартовых координатах

Уравнение

Если вводятся декартовы координаты так, что начало координат является центром гиперболы, а ось x является большой осью, то гипербола называется открывающейся с востока на запад, а

фокусы - это точки $F_{1}=(c,0),\ F_{2}=(-c,0)$,

вершины ​ ​ $V_{1}=(a,0),\ V_{2}=(-a,0)$.

Для произвольной точки $(x,y)$ расстояние до фокуса $(c,0)$ является ${\textstyle {\sqrt {(x-c)^{2}+y^{2}}}}$ и ко второму фокусу ${\textstyle {\sqrt {(x+c)^{2}+y^{2}}}}$. Отсюда и точка $(x,y)$ находится на гиперболе, если выполнено следующее условие

$${\sqrt {(x-c)^{2}+y^{2}}}-{\sqrt {(x+c)^{2}+y^{2}}}=\pm 2a\ .$$

Удалим квадратные корни путем подходящего возведения в квадрат и воспользуемся соотношением $b^{2}=c^{2}-a^{2}$ чтобы получить уравнение гиперболы:

$${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1\ .$$

Это уравнение называется канонической формой гиперболы, поскольку любую гиперболу, независимо от ее ориентации относительно декартовых осей и независимо от расположения ее центра, можно путем замены переменных привести к этой форме, дав гиперболу, соответствует оригиналу (см. ниже ).

Осями симметрии или главными осями являются поперечная ось (содержащая отрезок длиной 2 a с концами в вершинах) и сопряженная ось (содержащая отрезок длиной 2 b, перпендикулярный поперечной оси и со средней точкой в ​​центре гиперболы). . В отличие от эллипса, гипербола имеет только две вершины: $(a,0),\;(-a,0)$. Две точки $(0,b),\;(0,-b)$ на сопряженных осях не находятся на гиперболе.

Из уравнения следует, что гипербола симметрична относительно обеих координатных осей и, следовательно, симметрична относительно начала координат.

Эксцентриситет

Для гиперболы в указанной выше канонической форме эксцентриситет определяется выражением

$$e={\sqrt {1+{\frac {b^{2}}{a^{2}}}}}.$$

Две гиперболы геометрически подобны друг другу – это означает, что они имеют одинаковую форму, так что одну можно преобразовать в другую с помощью жестких движений влево и вправо , вращения , зеркального отображения и масштабирования (увеличения) – тогда и только тогда, когда у них одинаковая эксцентричность.

Асимптоты

Гипербола: полуоси а , б , линейный эксцентриситет с , полуширокая прямая кишка р

Гипербола: 3 объекта

Решение уравнения (выше) гиперболы для $y$ урожайность

$$y=\pm {\frac {b}{a}}{\sqrt {x^{2}-a^{2}}}.$$

Отсюда следует, что гипербола приближается к двум прямым

$$y=\pm {\frac {b}{a}}x$$

для больших значений $|x|$. Эти две прямые пересекаются в центре (начале координат) и называются асимптотами гиперболы. ${\tfrac {x^{2}}{a^{2}}}-{\tfrac {y^{2}}{b^{2}}}=1\ .$

С помощью второго рисунка можно увидеть, что

${\color {blue}{(1)}}$ Перпендикулярное расстояние от фокуса до любой асимптоты равно $b$ (малая полуось).

Из нормальной формы Гессена ${\tfrac {bx\pm ay}{\sqrt {a^{2}+b^{2}}}}=0$ из асимптот и уравнения гиперболы получаем:

${\color {magenta}{(2)}}$ Произведение расстояний от точки гиперболы до обеих асимптот есть константа ${\tfrac {a^{2}b^{2}}{a^{2}+b^{2}}}\ ,$ которое также можно записать через эксцентриситет e как $\left({\tfrac {b}{e}}\right)^{2}.$

Из уравнения $y=\pm {\frac {b}{a}}{\sqrt {x^{2}-a^{2}}}$ из гиперболы (см. выше) можно вывести:

${\color {green}{(3)}}$ Произведение наклонов линий от точки P до двух вершин есть константа $b^{2}/a^{2}\ .$

Кроме того, из (2) выше можно показать, что

${\color {red}{(4)}}$ Произведение расстояний от точки гиперболы до асимптот вдоль прямых, параллельных асимптотам, есть константа ${\tfrac {a^{2}+b^{2}}{4}}.$

Полупрямая сторона

Длина хорды через один из фокусов, перпендикулярную большой оси гиперболы, называется широкой прямой кишкой . Половина ее — полурасширенная прямая кишка. $p$. Расчет показывает

$$p={\frac {b^{2}}{a}}.$$

Полупрямая сторона $p$ также можно рассматривать как радиус кривизны вершин.

Касательная

Простейший способ определения уравнения касательной в точке $(x_{0},y_{0})$ заключается в неявном дифференцировании уравнения ${\tfrac {x^{2}}{a^{2}}}-{\tfrac {y^{2}}{b^{2}}}=1$ гиперболы. Обозначая dy/dx как y′ , это дает

$${\frac {2x}{a^{2}}}-{\frac {2yy'}{b^{2}}}=0\ \Rightarrow \ y'={\frac {x}{y}}{\frac {b^{2}}{a^{2}}}\ \Rightarrow \ y={\frac {x_{0}}{y_{0}}}{\frac {b^{2}}{a^{2}}}(x-x_{0})+y_{0}.$$

Что касается ${\tfrac {x_{0}^{2}}{a^{2}}}-{\tfrac {y_{0}^{2}}{b^{2}}}=1$, уравнение касательной в точке $(x_{0},y_{0})$ является

$${\frac {x_{0}}{a^{2}}}x-{\frac {y_{0}}{b^{2}}}y=1.$$

Особая касательная отличает гиперболу от других конических сечений. Пусть f — расстояние от вершины V (как по гиперболе, так и по ее оси, проходящей через два фокуса) до ближайшего фокуса. Тогда расстояние по линии, перпендикулярной этой оси, от этого фокуса до точки P на гиперболе больше 2 f . Касательная к гиперболе в точке P пересекает эту ось в точке Q под углом ∠PQV более 45°.

Прямоугольная гипербола

В случае $a=b$ Гипербола называется прямоугольной (или равносторонней ), потому что ее асимптоты пересекаются под прямым углом. В этом случае линейный эксцентриситет равен $c={\sqrt {2}}a$, эксцентриситет $e={\sqrt {2}}$ и полурасширенная прямая кишка $p=a$. График уравнения $y=1/x$ представляет собой прямоугольную гиперболу.

Параметрическое представление с гиперболическим синусом/косинусом

Использование гиперболических функций синуса и косинуса $\cosh ,\sinh$, параметрическое представление гиперболы ${\tfrac {x^{2}}{a^{2}}}-{\tfrac {y^{2}}{b^{2}}}=1$ можно получить, что аналогично параметрическому представлению эллипса:

$$(\pm a\cosh t,b\sinh t),\,t\in \mathbb {R} \ ,$$

которое удовлетворяет декартову уравнению, поскольку $\cosh ^{2}t-\sinh ^{2}t=1.$

Дополнительные параметрические представления приведены в разделе «Параметрические уравнения» ниже.

Здесь a = b = 1, что дает единичную гиперболу синего цвета и сопряженную с ней гиперболу зеленого цвета, имеющие одни и те же красные асимптоты.

Сопряженная гипербола

Основная статья: Сопряженная гипербола

Обмен ${\frac {x^{2}}{a^{2}}}$ и ${\frac {y^{2}}{b^{2}}}$ чтобы получить уравнение сопряженной гиперболы (см. схему):

$${\frac {y^{2}}{b^{2}}}-{\frac {x^{2}}{a^{2}}}=1\ ,$$

также написано как

$${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=-1\ .$$

Гипербола и ее сопряженная форма могут иметь сопряженные диаметры . теории В специальной относительности такие диаметры могут представлять собой оси времени и пространства, где одна гипербола представляет события на заданном пространственном расстоянии от центра , а другая представляет события на соответствующем временном расстоянии от центра.

В полярных координатах

Гипербола: полярные координаты с полюсом = фокус.

Гипербола: полярные координаты с полюсом = центру.

Анимированный сюжет Гиперболы с использованием $r={\frac {p}{1-e\cos \theta }}$

Происхождение в фокусе

Полярные координаты, используемые чаще всего для гиперболы, определяются относительно декартовой системы координат, начало которой находится в фокусе , а ось X указывает на начало «канонической системы координат», как показано на первой диаграмме.

В этом случае угол $\varphi$ называется истинной аномалией .

Относительно этой системы координат имеем

$$r={\frac {p}{1\mp e\cos \varphi }},\quad p={\frac {b^{2}}{a}}$$

и

$$-\arccos \left(-{\frac {1}{e}}\right)<\varphi <\arccos \left(-{\frac {1}{e}}\right).$$

Происхождение в центре

С полярными координатами относительно «канонической системы координат» (см. вторую диаграмму).у одного есть это

$$r={\frac {b}{\sqrt {e^{2}\cos ^{2}\varphi -1}}}.\,$$

Для правой ветви гиперболы диапазон значений $\varphi$ является

$$-\arccos \left({\frac {1}{e}}\right)<\varphi <\arccos \left({\frac {1}{e}}\right).$$

Параметрические уравнения

Гипербола с уравнением ${\tfrac {x^{2}}{a^{2}}}-{\tfrac {y^{2}}{b^{2}}}=1$ можно описать несколькими параметрическими уравнениями:

1. Через гиперболические тригонометрические функции
   $${\begin{cases}x=\pm a\cosh t,\\y=b\sinh t,\end{cases}}\qquad t\in \mathbb {R} .$$
2. Как рациональное представление
   $${\begin{cases}x=\pm a{\dfrac {t^{2}+1}{2t}},\\[1ex]y=b{\dfrac {t^{2}-1}{2t}},\end{cases}}\qquad t>0$$
3. Через круговые тригонометрические функции
   $${\begin{cases}x={\frac {a}{\cos t}}=a\sec t,\\y=\pm b\tan t,\end{cases}}\qquad 0\leq t<2\pi ,\ t\neq {\frac {\pi }{2}},\ t\neq {\frac {3}{2}}\pi .$$
4. С наклоном касательной в качестве параметра:
   Параметрическое представление, использующее наклон $m$ касательной в точке гиперболы можно получить аналогично случаю эллипса: Заменить в случае эллипса $b^{2}$ к $-b^{2}$ и использовать формулы для гиперболических функций . Получаешь
   $${\vec {c}}_{\pm }(m)=\left(-{\frac {ma^{2}}{\pm {\sqrt {m^{2}a^{2}-b^{2}}}}},{\frac {-b^{2}}{\pm {\sqrt {m^{2}a^{2}-b^{2}}}}}\right),\quad |m|>b/a.$$
   Здесь, ${\vec {c}}_{-}$ является верхним, и ${\vec {c}}_{+}$ нижняя половина гиперболы. Точки с вертикальными касательными (вершины $(\pm a,0)$) не покрываются представительством.
   Уравнение касательной в точке ${\vec {c}}_{\pm }(m)$ является
   $$y=mx\pm {\sqrt {m^{2}a^{2}-b^{2}}}.$$
   Это описание тангенсов гиперболы является важным инструментом для определения ортоптики гиперболы .

Гиперболические функции

Основная статья: Гиперболические функции

Луч, проходящий через единичную гиперболу $x^{2}\ -\ y^{2}\ =\ 1$ в точку $(\cosh \,a,\,\sinh \,a)$, где $a$ в два раза больше площади между лучом, гиперболой и $x$-ось. Для точек гиперболы ниже $x$-ось, площадь считается отрицательной.

Точно так же, как тригонометрические функции определяются в терминах единичной окружности , так и гиперболические функции определяются в терминах единичной гиперболы , как показано на этой диаграмме. В единичном круге угол (в радианах) равен удвоенной площади кругового сектора , на который опирается этот угол. Аналогичный гиперболический угол также определяется как удвоенная площадь гиперболического сектора .

Позволять $a$ быть в два раза больше площади между $x$ ось и луч, проходящий через начало координат, пересекающий единичную гиперболу, и определим ${\textstyle (x,y)=(\cosh a,\sinh a)=(x,{\sqrt {x^{2}-1}})}$ как координаты точки пересечения.Тогда площадь гиперболического сектора равна площади треугольника минус изогнутая область за вершиной в точке $(1,0)$:

$${\begin{aligned}{\frac {a}{2}}&={\frac {xy}{2}}-\int _{1}^{x}{\sqrt {t^{2}-1}}\,dt\\[1ex]&={\frac {1}{2}}\left(x{\sqrt {x^{2}-1}}\right)-{\frac {1}{2}}\left(x{\sqrt {x^{2}-1}}-\ln \left(x+{\sqrt {x^{2}-1}}\right)\right),\end{aligned}}$$

что упрощается до гиперболического косинуса площади

$$a=\operatorname {arcosh} x=\ln \left(x+{\sqrt {x^{2}-1}}\right).$$

Решение для $x$ дает экспоненциальную форму гиперболического косинуса:

$$x=\cosh a={\frac {e^{a}+e^{-a}}{2}}.$$

От $x^{2}-y^{2}=1$ каждый получает

$$y=\sinh a={\sqrt {\cosh ^{2}a-1}}={\frac {e^{a}-e^{-a}}{2}},$$

и обратный ему гиперболический синус площади :

$$a=\operatorname {arsinh} y=\ln \left(y+{\sqrt {y^{2}+1}}\right).$$

Другие гиперболические функции определяются в соответствии с гиперболическим косинусом и гиперболическим синусом, например

$$\operatorname {tanh} a={\frac {\sinh a}{\cosh a}}={\frac {e^{2a}-1}{e^{2a}+1}}.$$

Свойства

Свойство отражения

Гипербола: касательная делит линии, проходящие через фокусы, пополам.

Касательная в точке $P$ делит пополам угол между линиями ${\overline {PF_{1}}},{\overline {PF_{2}}}.$ Это называется оптическим свойством или свойством отражения гиперболы.

Доказательство

Позволять $L$ быть точкой на линии ${\overline {PF_{2}}}$ с расстоянием $2a$ в фокусе $F_{2}$ (см. схему, $a$ — большая полуось гиперболы). Линия $w$ - биссектриса угла между прямыми ${\overline {PF_{1}}},{\overline {PF_{2}}}$. Чтобы доказать это $w$ это касательная в точке $P$, проверяется, что любая точка $Q$ онлайн $w$ который отличается от $P$ не может находиться на гиперболе. Следовательно $w$ имеет только точку $P$ совпадает с гиперболой и, следовательно, является касательной в точке $P$.
Из диаграммы и неравенства треугольника видно, что $|QF_{2}|<|LF_{2}|+|QL|=2a+|QF_{1}|$ держится, что означает: $|QF_{2}|-|QF_{1}|<2a$. Но если $Q$ является точкой гиперболы, разность должна быть $2a$.

Середины параллельных хорд

Гипербола: середины параллельных хорд лежат на прямой.

Гипербола: середина хорды является серединой соответствующей хорды асимптот.

Середины параллельных хорд гиперболы лежат на прямой, проходящей через центр (см. схему).

Точки любой хорды могут лежать на разных ветвях гиперболы.

Доказательство свойства средних точек лучше всего проводить для гиперболы $y=1/x$. Потому что любая гипербола является аффинным образом гиперболы. $y=1/x$ (см. раздел ниже) и аффинное преобразование сохраняет параллельность и середины отрезков, это свойство справедливо для всех гипербол:
За два балла $P=\left(x_{1},{\tfrac {1}{x_{1}}}\right),\ Q=\left(x_{2},{\tfrac {1}{x_{2}}}\right)$ гиперболы $y=1/x$

середина аккорда это $M=\left({\tfrac {x_{1}+x_{2}}{2}},\cdots \right)=\cdots ={\tfrac {x_{1}+x_{2}}{2}}\;\left(1,{\tfrac {1}{x_{1}x_{2}}}\right)\ ;$

наклон хорды ${\frac {{\tfrac {1}{x_{2}}}-{\tfrac {1}{x_{1}}}}{x_{2}-x_{1}}}=\cdots =-{\tfrac {1}{x_{1}x_{2}}}\ .$

Для параллельных хорд наклон постоянен, а середины параллельных хорд лежат на прямой $y={\tfrac {1}{x_{1}x_{2}}}\;x\ .$

Следствие: для любой пары точек $P,Q$ хорды существует косое отражение с осью (набором неподвижных точек), проходящей через центр гиперболы, меняющей местами точки $P,Q$ и оставляет гиперболу (в целом) фиксированной. Косое отражение — это обобщение обычного отражения поперек линии. $m$, где все пары «точка-изображение» лежат на прямой, перпендикулярной $m$.

Поскольку косое отражение оставляет гиперболу фиксированной, пара асимптот также остается фиксированной. Отсюда и середина $M$ аккорда $PQ$ делит связанный сегмент прямой ${\overline {P}}\,{\overline {Q}}$ между асимптотами тоже пополам. Это означает, что $|P{\overline {P}}|=|Q{\overline {Q}}|$. Это свойство можно использовать для построения дальнейших точек. $Q$ гиперболы, если точка $P$ и даны асимптоты.

Если хорда вырождается в касательную , то точка касания делит отрезок между асимптотами на две половины.

Ортогональные касательные - ортоптические

Гипербола с ортоптическими (пурпурными)

Основная статья: Ортоптика (геометрия)

Для гиперболы ${\textstyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1,\,a>b}$ точки пересечения ортогональных касательных лежат на окружности $x^{2}+y^{2}=a^{2}-b^{2}$.
Эта окружность называется ортоптикой данной гиперболы.

Касательные могут принадлежать точкам на разных ветвях гиперболы.

В случае $a\leq b$ нет пар ортогональных касательных.

Полюсно-полярное

Гипербола: полюсно-полярное соотношение

Любую гиперболу можно описать в подходящей системе координат уравнением ${\tfrac {x^{2}}{a^{2}}}-{\tfrac {y^{2}}{b^{2}}}=1$. Уравнение касательной в точке $P_{0}=(x_{0},y_{0})$ гиперболы ${\tfrac {x_{0}x}{a^{2}}}-{\tfrac {y_{0}y}{b^{2}}}=1.$ Если допустить точку $P_{0}=(x_{0},y_{0})$ быть произвольной точкой, отличной от начала координат, то

точка $P_{0}=(x_{0},y_{0})\neq (0,0)$ отображается на линии ${\frac {x_{0}x}{a^{2}}}-{\frac {y_{0}y}{b^{2}}}=1$, а не через центр гиперболы.

Это отношение между точками и линиями является биекцией .

функция Обратная отображает

линия $y=mx+d,\ d\neq 0$ в точку $\left(-{\frac {ma^{2}}{d}},-{\frac {b^{2}}{d}}\right)$ и

линия $x=c,\ c\neq 0$ в точку $\left({\frac {a^{2}}{c}},0\right)\ .$

Такое отношение между точками и линиями, порожденное коникой, называется полюсно-полярным отношением или просто полярностью . Полюс – это точка, поляра – линия. См. Полюс и поляр .

Расчетом проверяются следующие свойства полюсно-полярного отношения гиперболы:

• Для точки (полюса) гиперболы полярой является касательная в этой точке (см. схему: $P_{1},\ p_{1}$).
• Для шеста $P$ вне гиперболы точки пересечения ее поляры с гиперболой являются точками касания двух касательных, проходящих $P$ (см. схему: $P_{2},\ p_{2},\ P_{3},\ p_{3}$).
• Для точки внутри гиперболы поляра не имеет общей точки с гиперболой. (см. схему: $P_{4},\ p_{4}$).

Примечания:

1. Точка пересечения двух поляр (например: $p_{2},p_{3}$) — полюс линии, проходящей через их полюса (здесь: $P_{2},P_{3}$).
2. Очаги $(c,0),$ и $(-c,0)$ соответственно и директрисы $x={\tfrac {a^{2}}{c}}$ и $x=-{\tfrac {a^{2}}{c}}$ соответственно принадлежат парам полюса и поляра.

Полюсно-полярные отношения существуют также для эллипсов и парабол.

Другая недвижимость

• Следующие элементы являются параллельными : (1) окружность, проходящая через фокусы гиперболы и с центром в центре гиперболы; (2) любая из прямых, касающихся гиперболы в вершинах; и (3) любая из асимптот гиперболы.
• Следующие элементы также являются параллельными: (1) окружность с центром в центре гиперболы и проходящая через вершины гиперболы; (2) любая директриса; и (3) любая из асимптот.

Длина дуги

Длина дуги гиперболы не имеет элементарного выражения . Верхнюю половину гиперболы можно параметризовать как

$$y=b{\sqrt {{\frac {x^{2}}{a^{2}}}-1}}.$$

Тогда интеграл, дающий длину дуги $s$ от $x_{1}$ к $x_{2}$ можно вычислить как:

$$s=b\int _{\operatorname {arcosh} {\frac {x_{1}}{a}}}^{\operatorname {arcosh} {\frac {x_{2}}{a}}}{\sqrt {1+\left(1+{\frac {a^{2}}{b^{2}}}\right)\sinh ^{2}v}}\,\mathrm {d} v.$$

После использования замены $z=iv$, это также можно представить с помощью неполного эллиптического интеграла второго рода $E$ с параметром $m=k^{2}$:

$$s=ib{\Biggr [}E\left(iv\,{\Biggr |}\,1+{\frac {a^{2}}{b^{2}}}\right){\Biggr ]}_{\operatorname {arcosh} {\frac {x_{2}}{a}}}^{\operatorname {arcosh} {\frac {x_{1}}{a}}}.$$

Используя только действительные числа, это становится

$$s=b\left[F\left(\operatorname {gd} v\,{\Biggr |}-{\frac {a^{2}}{b^{2}}}\right)-E\left(\operatorname {gd} v\,{\Biggr |}-{\frac {a^{2}}{b^{2}}}\right)+{\sqrt {1+{\frac {a^{2}}{b^{2}}}\tanh ^{2}v}}\,\sinh v\right]_{\operatorname {arcosh} {\tfrac {x_{1}}{a}}}^{\operatorname {arcosh} {\tfrac {x_{2}}{a}}}$$

где $F$ – неполный эллиптический интеграл первого рода с параметром $m=k^{2}$ и $\operatorname {gd} v=\arctan \sinh v$ – функция Гудермана .

Производные кривые

Синусоидальные спирали ( r ^н = –1 ^н cos( nθ ), θ = π /2 ) в полярных координатах и ​​их эквиваленты в прямоугольных координатах :

  n = −2 : равносторонняя гипербола

  n = −1 : линия

  n = −1/2 : Парабола

  n = 1/2 : Кардиоида

  n = 1 : Круг

  n = 2 : лемниската Бернулли.

из гиперболы можно получить еще несколько кривых Путем обращения , так называемые обратные кривые гиперболы. Если центр инверсии выбран в качестве собственного центра гиперболы, обратная кривая является лемнискатой Бернулли ; лемниската также представляет собой оболочку кругов с центром в прямоугольной гиперболе и проходящую через начало координат. Если центр инверсии выбран в фокусе или вершине гиперболы, полученные обратные кривые представляют собой лимасон или строфоид соответственно .

Эллиптические координаты

Семейство софокусных гипербол является основой системы эллиптических координат в двух измерениях. Эти гиперболы описываются уравнением

$$\left({\frac {x}{c\cos \theta }}\right)^{2}-\left({\frac {y}{c\sin \theta }}\right)^{2}=1$$

где фокусы расположены на расстоянии c от начала координат по оси x , и где θ - угол асимптот с осью x . Каждая гипербола в этом семействе ортогональна каждому эллипсу, имеющему одинаковые фокусы. Эту ортогональность можно показать с помощью конформного отображения декартовой системы координат w = z + 1/ z , где z = x + iy — исходные декартовы координаты, а w = u + iv — координаты после преобразования.

Другие ортогональные двумерные системы координат, включающие гиперболы, могут быть получены с помощью других конформных отображений. Например, отображение w = z ² преобразует декартову систему координат в два семейства ортогональных гипербол.

кругов

Центральная проекция кругов на сферу: центр O проекции находится внутри сферы, плоскость изображения красная.
В качестве изображений кругов получаются круг (пурпурный), эллипсы, гиперболы и линии. Особый случай параболы в этом примере не проявляется.
(Если бы центр О находился на сфере, все изображения кругов были бы кругами или линиями; см. стереографическую проекцию ).

Помимо обеспечения единообразного описания кругов, эллипсов, парабол и гипербол, конические сечения также можно понимать как естественную модель геометрии перспективы в том случае, когда просматриваемая сцена состоит из кругов или, в более общем смысле, эллипса. Зрителем обычно является камера или человеческий глаз, а изображение сцены — это центральная проекция на плоскость изображения, то есть все проекционные лучи проходят через фиксированную точку O , центр. Плоскость линзы параллельная плоскости изображения линзы O. — это плоскость ,

Изображение круга c есть

1. круг , , если круг c находится в особом положении, например параллельно плоскости изображения и др. (см. стереографическую проекцию)
2. эллипс c , если не общей имеет точки с плоскостью линзы,
3. парабола , если с имеет одну общую точку с плоскостью линзы и
4. гипербола . , если c имеет две общие точки с плоскостью линзы

(Особые положения, в которых плоскость окружности содержит точку O, опущены.)

Эти результаты можно понять, если признать, что процесс проецирования можно рассматривать в два этапа: 1) круг c и точка O образуют конус, который 2) разрезается плоскостью изображения для создания изображения.

Гиперболу можно увидеть всякий раз, когда замечаешь часть круга, пересекаемую плоскостью линзы. Неспособность видеть большую часть ветвей видимой ветви в сочетании с полным отсутствием второй ветви делает практически невозможным для зрительной системы человека распознавание связи с гиперболами.

Приложения

Гиперболы как линии склонения на солнечных часах.

горизонтального сверхзвукового самолета Зона контакта ударной волны с плоской землей (желтая) является частью гиперболы, поскольку земля пересекает конус параллельно ее оси.

Солнечные часы

Гиперболы можно увидеть на многих солнечных часах . В любой день солнце вращается по кругу на небесной сфере , и его лучи, попадая в точку солнечных часов, очерчивают конус света. Пересечение этого конуса с горизонтальной плоскостью земли образует коническое сечение. В большинстве населенных широт и в большинстве времен года это коническое сечение представляет собой гиперболу. На практике тень кончика шеста в течение суток очерчивает на земле гиперболу (этот путь называется линией склонения ). Форма этой гиперболы меняется в зависимости от географической широты и времени года, поскольку эти факторы влияют на конус солнечных лучей относительно горизонта. Собрание таких гипербол в течение целого года в заданном месте греки называли пелекинон , так как он напоминает двулезвийный топор.

Мультилатерация

Гипербола является основой решения задач мультилатерации , задачи определения местоположения точки по разностям ее расстояний до заданных точек — или, что то же самое, по разнице времен прихода синхронизированных сигналов между точкой и заданными точками. Подобные проблемы важны в судоходстве, особенно на воде; корабль может определить свое положение по разнице во времени прибытия сигналов от передатчиков LORAN или GPS . И наоборот, самонаводящийся маяк или любой передатчик можно определить путем сравнения времени прибытия его сигналов на две отдельные приемные станции; такие методы могут использоваться для отслеживания объектов и людей. В частности, множество возможных положений точки, которая имеет разницу расстояний 2 a от двух заданных точек, представляет собой гиперболу с расстоянием между вершинами 2 a, фокусами которой являются две заданные точки.

Путь, по которому следует частица

Путь, по которому движется любая частица в классической задаче Кеплера, представляет собой коническое сечение . В частности, если полная энергия E частицы больше нуля (т. е. если частица несвязана), путь такой частицы представляет собой гиперболу. Это свойство полезно при изучении атомных и субатомных сил путем рассеяния частиц высокой энергии; например, эксперимент Резерфорда продемонстрировал существование атомного ядра , исследуя рассеяние альфа-частиц на золота атомах . Если короткодействующие ядерные взаимодействия игнорируются, атомное ядро ​​и альфа-частица взаимодействуют только посредством отталкивающей силы Кулона , которая удовлетворяет требованию закона обратных квадратов для задачи Кеплера.

Кортевега –

Гиперболическая триггерная функция $\operatorname {sech} \,x$ появляется как одно из решений уравнения Кортевега – де Фриза , описывающего движение солитонной волны в канале.

Угловая трисекция

Трисекция угла (AOB) с использованием гиперболы с эксцентриситетом 2 (желтая кривая)

Как впервые показал Аполлоний Пергский , гиперболу можно использовать для разделения любого угла пополам — это хорошо изученная задача геометрии. Учитывая угол, сначала нарисуйте круг с центром в его вершине , который пересекает стороны угла в точках A и B. O Затем нарисуйте отрезок с конечными точками A и B и его серединный перпендикуляр. $\ell$. Постройте гиперболу эксцентриситета e =2 с $\ell$ как директриса и B как фокус. Пусть P — пересечение (верхнее) гиперболы с окружностью. Угол POB делит угол AOB на три части .

Чтобы доказать это, отразите отрезок ОП о прямой $\ell$ получение точки P' как образа P . Отрезок AP' имеет ту же длину, что и сегмент BP, из-за отражения, а сегмент PP' имеет ту же длину, что и сегмент BP, из-за эксцентриситета гиперболы. Поскольку OA , OP' , OP и OB являются радиусами одной и той же окружности (и, следовательно, имеют одинаковую длину), треугольники OAP' , OPP' и OPB конгруэнтны. Следовательно, угол был разделен на три части, поскольку 3× POB = AOB .

портфеля

В теории портфеля местоположение эффективных портфелей средней дисперсии (так называемая эффективная граница) представляет собой верхнюю половину ветви гиперболы, открывающейся на восток, нарисованной со стандартным отклонением доходности портфеля, нанесенным горизонтально, и его ожидаемым значением, нанесенным вертикально; согласно этой теории, все рациональные инвесторы выберут портфель, характеризующийся некоторой точкой в ​​этом локусе.

Биохимия

В биохимии и фармакологии уравнение Хилла и уравнение Хилла-Лэнгмюра соответственно описывают биологические реакции и образование комплексов белок-лиганд в зависимости от концентрации лиганда. Обе они представляют собой прямоугольные гиперболы.

Гиперболы как плоские сечения квадрик

Гиперболы представляют собой плоские сечения следующих квадрик :

• Эллиптический конус
• Гиперболический цилиндр
• Гиперболический параболоид
• Гиперболоид одного листа
• Гиперболоид из двух листов

• 
  Эллиптический конус
• 
  Гиперболический цилиндр
• 
  Гиперболический параболоид
• 
  Гиперболоид одного листа
• 
  Гиперболоид из двух листов

См. также

Другие конические сечения

• Круг
• Эллипс
• Парабола
• Вырожденная коническая

Другие похожие темы

• Эллиптические координаты — ортогональная система координат, основанная на семействах эллипсов и гипербол.
• Гиперболический рост
• Гиперболическое уравнение в частных производных
• Гиперболический сектор
• Гиперболоидная структура
• Гиперболическая траектория
• Гиперболоид
• Мультилатерация
• Вращение осей
• Перевод осей
• Единичная гипербола

Ссылки

• Казаринов, Николас Д. (1970), Правитель и раунд , Бостон: Приндл, Вебер и Шмидт, ISBN  0-87150-113-9
• Окли, Колорадо, доктор философии. (1944), Очерк исчисления , Нью-Йорк: Barnes & Noble. {{citation}}: CS1 maint: несколько имен: список авторов ( ссылка )
• Проттер, Мюррей Х .; Морри, Чарльз Б. младший (1970), Колледжское исчисление с аналитической геометрией (2-е изд.), Чтение: Аддисон-Уэсли , LCCN   76087042

Внешние ссылки

• «Гипербола» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Вывод Аполлонием гиперболы при конвергенции
• Франс ван Скутен: Математические упражнения , 1659 г.
• Вайсштейн, Эрик В. «Гипербола» . Математический мир .