Эксцентриситет (математика)

Семейство конических сечений с разным эксцентриситетом имеет общую точку фокуса и направляющую линию, включая эллипс (красный, $e = 1/2$ ), параболу (зеленый, $e = 1$ ) и гиперболу (синий, $e = 2$ ). Коника эксцентриситета $0$ на этом рисунке представляет собой бесконечно малую окружность с центром в фокусе, а коника эксцентриситета $\infty$ — бесконечно мало разделенную пару прямых.
Окружность конечного радиуса имеет бесконечно удаленную направляющую, а пара линий конечного разделения имеет бесконечно удаленный фокус.

В математике эксцентриситет . конического сечения — это неотрицательное действительное число, однозначно характеризующее его форму

Эксцентриситет можно рассматривать как меру того, насколько коническое сечение отклоняется от круглого. В частности:

Эксцентриситет окружности равен 0.
Эксцентриситет эллипса , не являющегося кругом, находится в диапазоне от 0 до 1.
Эксцентриситет параболы равен 1.
Эксцентриситет гиперболы больше 1.
Эксцентриситет пары прямых равен $\infty$

Два конических сечения с одинаковым эксцентриситетом подобны .

Определения [ править ]

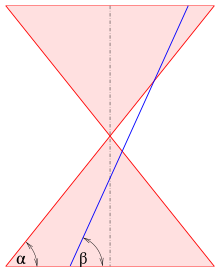
Любое коническое сечение можно определить как геометрическое место точек , расстояния до которых до точки (фокуса) и прямой (директрисы) находятся в постоянном соотношении. Это соотношение называется эксцентриситетом, обычно обозначаемым как $e$ .

Эксцентриситет также можно определить как пересечение плоскости и конуса с двойным ворсом, связанного с коническим сечением. Если конус ориентирован своей осью вертикально, эксцентриситет равен ^[1]

e={\frac {\sin \beta }{\sin \alpha }},\ \ 0<\alpha <90^{\circ },\ 0\leq \beta \leq 90^{\circ }\ ,

где β — угол между плоскостью и горизонталью, а α — угол между образующей наклона конуса и горизонталью. Для $\beta =0$ плоское сечение представляет собой круг, т.к. $\beta =\alpha$ парабола. (Плоскость не должна совпадать с вершиной конуса.)

Полуфокусное расстояние эллипса или гиперболы, обозначаемое $c$ (или иногда $f$ или $e$ ), представляет собой расстояние между его центром и любым из двух его фокусов . Эксцентриситет можно определить как отношение полуфокального расстояния к большой полуоси $a$ : то есть, $e={\frac {c}{a}}$ (без центра полуфокальное расстояние для парабол не определено). Стоит отметить, что параболу можно рассматривать как эллипс или гиперболу, но с одним фокусом на бесконечности .

Альтернативные названия [ править ]

В случае эллипсов и гипербол полуфокальное расстояние иногда называют линейным эксцентриситетом .

Обозначения [ править ]

Обычно используются три соглашения об обозначениях:

$e$ для эксцентриситета и $c$ для полуфокального разделения.

Ценности [ править ]

Коническое сечение	Уравнение	Эксцентриситет ( $е$ )	Линейный эксцентриситет ( $c$ )
Круг	$x^{2}+y^{2}=r^{2}$	$0$	$0$
Эллипс	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$ или ${\frac {y^{2}}{a^{2}}}+{\frac {x^{2}}{b^{2}}}=1$ где $a>b$	${\sqrt {1-{\frac {b^{2}}{a^{2}}}}}$	${\sqrt {a^{2}-b^{2}}}$
Парабола	$x^{2}=4ay$	$1$	неопределенный ( $\infty$ )
Гипербола	${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1$ или ${\frac {y^{2}}{a^{2}}}-{\frac {x^{2}}{b^{2}}}=1$	${\sqrt {1+{\frac {b^{2}}{a^{2}}}}}$	${\sqrt {a^{2}+b^{2}}}$

Здесь для эллипса и гиперболы $a$ — длина большой полуоси, а $b$ — длина малой полуоси.

Когда коническое сечение задано в общей квадратичной форме

Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0,

следующая формула дает эксцентриситет $e,$ если коническое сечение не является параболой (эксцентриситет которой равен 1), не вырожденной гиперболой или вырожденным эллипсом и не воображаемым эллипсом: ^[2]

e={\sqrt {\frac {2{\sqrt {(A-C)^{2}+B^{2}}}}{\eta (A+C)+{\sqrt {(A-C)^{2}+B^{2}}}}}}

где $\eta =1$ если определитель матрицы 3×3

{\begin{bmatrix}A&B/2&D/2\\B/2&C&E/2\\D/2&E/2&F\end{bmatrix}}

является отрицательным или $\eta =-1$ если этот определитель положителен.

Эллипсы [ править ]

Эксцентриситет эллипса строго меньше 1. Когда круги (которые имеют эксцентриситет 0) считаются эллипсами, эксцентриситет эллипса больше или равен 0; если кругам отдать специальную категорию и исключить их из категории эллипсов, то эксцентриситет эллипса строго больше 0.

Для любого эллипса пусть $a$ — длина его большой полуоси , а $b$ — длина его малой полуоси . В системе координат с началом координат в центре эллипса и $осью x$ , совмещенной с большой осью, точки эллипса удовлетворяют уравнению

{\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1,

с фокусами по координатам $(\pm c,0)$ для ${\textstyle c={\sqrt {a^{2}-b^{2}}}.}$

Определим ряд сопутствующих дополнительных понятий (только для эллипсов):

Имя	Символ	с точки зрения $а$ и $б$	с точки зрения $е$
Первый эксцентриситет	$e$	${\sqrt {1-{\frac {b^{2}}{a^{2}}}}}$	$e$
Второй эксцентриситет	$e'$	${\sqrt {{\frac {a^{2}}{b^{2}}}-1}}$	${\frac {e}{\sqrt {1-e^{2}}}}$
Третий эксцентриситет	$e''={\sqrt {m}}$	${\frac {\sqrt {a^{2}-b^{2}}}{\sqrt {a^{2}+b^{2}}}}$	${\frac {e}{\sqrt {2-e^{2}}}}$
Угловой эксцентриситет	$\alpha$	$\cos ^{-1}\left({\frac {b}{a}}\right)$	$\sin ^{-1}e$

Другие формулы эксцентриситета эллипса [ править ]

Эксцентриситет эллипса проще всего представляет собой отношение линейного эксцентриситета $c$ (расстояния между центром эллипса и каждым фокусом) к длине большой полуоси $a$ .

e={\frac {c}{a}}.

Эксцентриситет - это также отношение большой полуоси $a$ к расстоянию $d$ от центра до направляющей:

e={\frac {a}{d}}.

Эксцентриситет можно выразить через сплющивание $f$ (определяемое как $f=1-b/a$ для большой полуоси $a$ и малой полуоси $b$ ):

e={\sqrt {1-(1-f)^{2}}}={\sqrt {f(2-f)}}.

сплющивание может обозначаться буквой $g,$ ( В некоторых предметных областях $если f$ — линейный эксцентриситет.)

Определите максимальный и минимальный радиусы $r_{\text{max}}$ и $r_{\text{min}}$ как максимальное и минимальное расстояния от любого фокуса до эллипса (то есть расстояния от любого фокуса до двух концов большой оси). Тогда с большой полуосью $a$ эксцентриситет определяется выражением

e={\frac {r_{\text{max}}-r_{\text{min}}}{r_{\text{max}}+r_{\text{min}}}}={\frac {r_{\text{max}}-r_{\text{min}}}{2a}},

которое представляет собой расстояние между фокусами, деленное на длину большой оси.

Гиперболы [ править ]

Эксцентриситет гиперболы может быть любым действительным числом больше 1, без верхней границы. Эксцентриситет прямоугольной гиперболы равен ${\sqrt {2}}$ .

Квадрика [ править ]

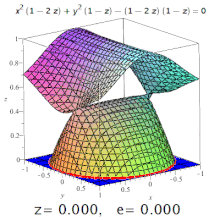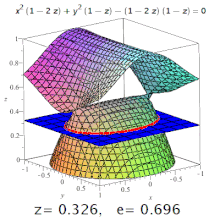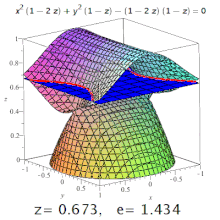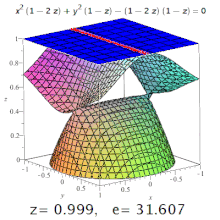
Эксцентриситет трехмерной квадрики — это эксцентриситет обозначенного участка ее . Например, на трехосном эллипсоиде меридиональный эксцентриситет — это эксцентриситет эллипса, образованного секцией, содержащей как самую длинную, так и самую короткую оси (одна из которых будет полярной осью), а экваториальный эксцентриситет — это эксцентриситет образованного эллипса. разрезом через центр, перпендикулярно полярной оси (т.е. в экваториальной плоскости). Но: конические сечения могут встречаться и на поверхностях более высокого порядка (см. Изображение).

Небесная механика [ править ]

В небесной механике для связанных орбит в сферическом потенциале приведенное выше определение является неформальным обобщением. Когда расстояние апоцентра близко к расстоянию перицентра , говорят, что орбита имеет низкий эксцентриситет; когда они сильно различаются, говорят, что орбита эксцентрична или имеет эксцентриситет, близкий к единице. Это определение совпадает с математическим определением эксцентриситета эллипсов в кеплеровском языке, т.е. $1/r$ потенциалы.

классификации Аналогичные

В ряде классификаций в математике используется терминология, производная от классификации конических сечений по эксцентриситету:

Классификация элементов SL классификации ₂ (R) на эллиптические, параболические и гиперболические – и аналогично для элементов PSL ₂ (R) вещественных преобразований Мёбиуса .
Классификация дискретных распределений по отношению дисперсии к среднему ; см . в кумулянтах некоторых дискретных распределений вероятностей . подробности
Классификация уравнений в частных производных проводится по аналогии с классификацией конических сечений; см. эллиптические , параболические и гиперболические уравнения в частных производных. ^[3]

См. также [ править ]

Ссылки [ править ]

^ Томас, Джордж Б.; Финни, Росс Л. (1979), Исчисление и аналитическая геометрия (пятое изд.), Аддисон-Уэсли, с. 434. ISBN 0-201-07540-7
^ Аюб, Аюб Б., «Эксцентриситет конического сечения», The College Mathematics Journal 34 (2), март 2003 г., 116–121.
^ «Классификация линейных УЧП с двумя независимыми переменными» . Проверено 2 июля 2013 г.

Внешние ссылки [ править ]

MathWorld: Эксцентриситет

[1] Томас, Джордж Б.; Финни, Росс Л. (1979), Исчисление и аналитическая геометрия (пятое изд.), Аддисон-Уэсли, с. 434. ISBN 0-201-07540-7

[2] Аюб, Аюб Б., «Эксцентриситет конического сечения», The College Mathematics Journal 34 (2), март 2003 г., 116–121.

[ornl.gov-3] «Классификация линейных УЧП с двумя независимыми переменными» . Проверено 2 июля 2013 г.

[1]

[2]

[3]