Средняя аномалия

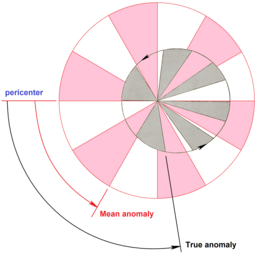
В небесной механике средняя аномалия — это доля периода эллиптической орбиты , прошедшая с тех пор, как вращающееся тело прошло перицентр , выраженная как угол , который можно использовать при вычислении положения этого тела в классической задаче двух тел . Это угловое расстояние от перицентра , которое имело бы фиктивное тело, если бы оно двигалось по круговой орбите с постоянной скоростью за тот же период обращения , что и реальное тело на своей эллиптической орбите. ^[1]^[2]

Определение

Определите $T$ как время, необходимое конкретному телу для совершения одного оборота. За время $T$ выметается радиус-вектор на 2 $π$ радиан, или 360°. Средняя скорость развертки $n$ тогда равна

$n={\frac {\,2\,\pi \,}{T}}={\frac {\,360^{\circ }\,}{T}}~,$

которое называется средним угловым движением тела с размерами в радианах в единицу времени или в градусах в единицу времени.

Определим $τ$ как время, в которое тело находится в перицентре. новую величину $M$ , среднюю аномалию. Из приведенных выше определений можно определить

$M=n\,(t-\tau )~,$

что дает угловое расстояние от перицентра в произвольный момент времени $t$ . ^[3] с размерами в радианах или градусах.

Поскольку скорость увеличения $n$ является постоянным средним значением, средняя аномалия увеличивается равномерно (линейно) от 0 до 2 $π$ радиан или от 0 ° до 360 ° на каждом витке. Он равен 0, когда тело находится в перицентре, $π$ радиан (180°) в апоцентре и 2 $π$ радиан (360°) после одного полного оборота. ^[4] Если средняя аномалия известна в любой момент времени, ее можно рассчитать в любой более поздний (или предыдущий) момент, просто добавив (или вычитая) $n\cdotδt$ , где $δt$ представляет собой небольшую разницу во времени.

Средняя аномалия не измеряет угол между какими-либо физическими объектами (кроме перицентра или апоцентра или круговой орбиты). Это просто удобная единая мера того, насколько далеко тело продвинулось по своей орбите от перицентра. Средняя аномалия — это один из трёх угловых параметров (исторически известных как «аномалии»), определяющих положение на орбите, два других — эксцентрическая аномалия и истинная аномалия .

Формулы

Средняя аномалия $M$ может быть вычислена из эксцентрической аномалии $E$ и эксцентриситета $e$ с помощью уравнения Кеплера :

$M=E-e\,\sin E~.$

Средняя аномалия также часто рассматривается как

$M=M_{0}+n\left(t-t_{0}\right)~,$

где $M$ ₀ — средняя аномалия в эпоху , а $t$ ₀ — эпоха , эталонное время, к которому относятся элементы орбиты , которое может совпадать или не совпадать с $τ$ , временем прохождения перицентра. Классический метод определения положения объекта на эллиптической орбите по набору элементов орбиты заключается в вычислении средней аномалии по этому уравнению, а затем в решении уравнения Кеплера для эксцентрической аномалии.

Определите $ϖ$ как долготу перицентра , угловое расстояние перицентра от опорного направления. Определите $ℓ$ как среднюю долготу , угловое расстояние тела от того же исходного направления, предполагая, что оно движется с равномерным угловым движением, как и в случае средней аномалии. Таким образом, средняя аномалия также ^[5]

M=\ell -\varpi ~.

Среднее угловое движение также можно выразить как

$n={\sqrt {{\frac {\mu }{\;a^{3}\,}}\,}}~,$

где $μ$ — гравитационный параметр , который меняется в зависимости от массы объектов, а $a$ — большая полуось орбиты. Затем среднюю аномалию можно расширить,

$M={\sqrt {{\frac {\mu }{\;a^{3}\,}}\,}}\,\left(t-\tau \right)~,$

и здесь средняя аномалия представляет собой равномерное угловое движение по окружности радиуса $a$ . ^[6]

Средняя аномалия может быть рассчитана на основе эксцентриситета и истинной аномалии $f,$ найдя эксцентрическую аномалию и затем используя уравнение Кеплера. Это дает в радианах: $M=\operatorname {atan2} \left(-\ {\sqrt {1-e^{2}}}\sin f,-\ e-\cos f\right)+\pi -e{\frac {{\sqrt {1-e^{2}}}\sin f}{1+e\cos f}}$ где atan2 (y,x) — угол от оси x луча от (0,0) до (x,y), имеющего тот же знак, что и y. , аргументы часто меняются местами (Обратите внимание, что в электронных таблицах, например Excel .)

Для параболических и гиперболических траекторий средняя аномалия не определена, поскольку они не имеют периода. Но в этих случаях, как и в случае эллиптических орбит, площадь, охватываемая хордой между аттрактором и объектом, следующим по траектории, линейно увеличивается со временем. Для гиперболического случая существует формула, аналогичная приведенной выше, дающая прошедшее время как функцию угла (истинная аномалия в эллиптическом случае), как объяснено в статье « Орбита Кеплера» . Для параболического случая существует другая формула: предельный случай для эллиптического или гиперболического случая, когда расстояние между фокусами стремится к бесконечности – см. Параболическая траектория # Уравнение Баркера .

Средняя аномалия также может быть выражена в виде разложения в ряд : ^[7] $M=f+2\sum _{n=1}^{\infty }(-1)^{n}\left[{\frac {1}{n}}+{\sqrt {1-e^{2}}}\right]\beta ^{n}\sin {nf}$

с $\beta ={\frac {1-{\sqrt {1-e^{2}}}}{e}}$

$M=f-2\,e\sin f+\left({\frac {3}{4}}e^{2}+{\frac {1}{8}}e^{4}\right)\sin 2f-{\frac {1}{3}}e^{3}\sin 3f+{\frac {5}{32}}e^{4}\sin 4f+\operatorname {\mathcal {O}} \left(e^{5}\right)$

Аналогичная формула дает истинную аномалию непосредственно через среднюю аномалию: ^[8]

$f=M+\left(2\,e-{\frac {1}{4}}e^{3}\right)\sin M+{\frac {5}{4}}e^{2}\sin 2M+{\frac {13}{12}}e^{3}\sin 3M+\operatorname {\mathcal {O}} \left(e^{4}\right)$

Общую формулировку приведенного выше уравнения можно записать как уравнение центра : ^[9]

$f=M+2\sum _{s=1}^{\infty }{\frac {1}{s}}\left[J_{s}(se)+\sum _{p=1}^{\infty }\beta ^{p}{\big (}J_{s-p}(se)+J_{s+p}(se){\big )}\right]\sin(sM)$

См. также

Ссылки

^ Монтенбрук, Оливер (1989). Практические расчеты эфемерид . Спрингер-Верлаг . п. 44 . ISBN 0-387-50704-3 .
^ Меус, Жан (1991). Астрономические алгоритмы . Willmann-Bell, Inc., Ричмонд, Вирджиния. п. 182 . ISBN 0-943396-35-2 .
^ Смарт, WM (1977). Учебник по сферической астрономии (шестое изд.). Издательство Кембриджского университета, Кембридж. п. 113. ИСБН 0-521-29180-1 .
^ Меус (1991), с. 183
^ Смарт (1977), с. 122
^ Валладо, Дэвид А. (2001). Основы астродинамики и приложений (2-е изд.). Эль Сегундо, Калифорния: Microcosm Press. стр. 53–54. ISBN 1-881883-12-4 .
^ Смарт, WM (1953). Небесная механика . Лондон, Великобритания: Longmans, Green, and Co. p. 38.
^ Рой, А.Е. (1988). Орбитальное движение (1-е изд.). Бристоль, Великобритания; Филадельфия, Пенсильвания: А. Хилгер. ISBN 0852743602 .
^ Брауэр, Дирк (1961). Методы небесной механики . Эльзевир. стр. например 77.

Внешние ссылки

Аномалия записи в глоссарии , среднее значение. Архивировано 23 декабря 2017 г. в Wayback Machine Военно-морской обсерватории США. в онлайн-альманахе Архивировано 20 апреля 2015 г. в Wayback Machine.

[1] Монтенбрук, Оливер (1989). Практические расчеты эфемерид . Спрингер-Верлаг . п. 44 . ISBN 0-387-50704-3 .

[2] Меус, Жан (1991). Астрономические алгоритмы . Willmann-Bell, Inc., Ричмонд, Вирджиния. п. 182 . ISBN 0-943396-35-2 .

[3] Смарт, WM (1977). Учебник по сферической астрономии (шестое изд.). Издательство Кембриджского университета, Кембридж. п. 113. ИСБН 0-521-29180-1 .

[4] Меус (1991), с. 183

[5] Смарт (1977), с. 122

[6] Валладо, Дэвид А. (2001). Основы астродинамики и приложений (2-е изд.). Эль Сегундо, Калифорния: Microcosm Press. стр. 53–54. ISBN 1-881883-12-4 .

[7] Смарт, WM (1953). Небесная механика . Лондон, Великобритания: Longmans, Green, and Co. p. 38.

[8] Рой, А.Е. (1988). Орбитальное движение (1-е изд.). Бристоль, Великобритания; Филадельфия, Пенсильвания: А. Хилгер. ISBN 0852743602 .

[9] Брауэр, Дирк (1961). Методы небесной механики . Эльзевир. стр. например 77.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]