Атан2

График $\operatorname {atan2} (y,x)$ над $y/x$

В вычислительной технике и математике функция представляет собой atan2 с двумя аргументами арктангенс . По определению, $\theta =\operatorname {atan2} (y,x)$ — мера угла (в радианах , с $-\pi <\theta \leq \pi$ ) между положительными $x$ -ось и луч от начала координат до точки $(x,\,y)$ в декартовой плоскости . Эквивалентно, $\operatorname {atan2} (y,x)$ — аргумент (также называемый фазой или углом ) комплексного числа $x+iy.$

The $\operatorname {atan2}$ Функция впервые появилась в языке программирования Фортран в 1961 году. Изначально она предназначалась для возврата правильного и однозначного значения угла $θ$ при преобразовании из декартовых координат $(x, y)$ в полярные координаты $(r, θ)$ . Если $\theta =\operatorname {atan2} (y,x)$ и ${\textstyle r={\sqrt {x^{2}+y^{2}}}}$ , затем $x=r\cos \theta$ и $y=r\sin \theta .$

Если $x > 0$ , желаемая угловая мера равна ${\textstyle \theta =\operatorname {atan2} (y,x)=\arctan \left(y/x\right).}$ Однако, когда $x < 0$ , угол $\arctan(y/x)$ диаметрально противоположен желаемому углу, и необходимо добавить ± $π$ (полоборота ) , чтобы поместить точку в правильный квадрант . ^[1] Используя $\operatorname {atan2}$ функция устраняет эту коррекцию, упрощая код и математические формулы.

Мотивация [ править ]

Обычная функция арктангенса с одним аргументом возвращает только угловые значения в интервале ${\textstyle {\left(-{\frac {\pi }{2}},+{\frac {\pi }{2}}\right)},}$ и при его вызове для нахождения меры угла между $осью x$ и произвольным вектором в декартовой плоскости не существует простого способа указать направление в левой полуплоскости (то есть точку $(x,\,y)$ с $x<0$ ). Диаметрально противоположные угловые меры имеют одинаковый тангенс, поскольку $y/x=(-y)/(-x),$ так что касательная $y/x$ само по себе недостаточно для однозначного определения угла.

Чтобы определить величину угла с помощью функции арктангенса по заданной точке или вектору. $(x,y),$ математические формулы или компьютерный код должны обрабатывать несколько случаев; хотя бы один для положительных значений $x$ и один для отрицательных значений $x,$ а иногда и дополнительные случаи, когда $y$ отрицательно или одна координата равна нулю. Поиск угловых мер и преобразование декартовых координат в полярные широко распространены в научных вычислениях, и этот код является избыточным и подвержен ошибкам.

Чтобы исправить это, в языках программирования была введена $функция atan2$ , по крайней мере, еще в языке Fortran IV 1960-х годов. ^[2]Величина $atan2(y, x)$ является мерой угла между $осью x$ и лучом от начала координат до точки $(x, y)$ в любом месте декартовой плоскости. Знаки x y $)$ и $/$ используются для определения результата и выбора правильной ветви функции $Arctan(y многозначной x .$ квадранта

Функция $atan2$ полезна во многих приложениях, связанных с евклидовыми векторами, таких как поиск направления от одной точки к другой или преобразование матрицы вращения в углы Эйлера .

Функция $atan2$ теперь включена во многие другие языки программирования, а также часто встречается в математических формулах науки и техники.

Порядок аргументов [ править ]

В 1961 году Фортран представил $функцию atan2$ с порядком аргументов. $(y,x)$ так что аргумент (фазовый угол) комплексного числа равен $\operatorname {arg} z=\operatorname {atan2} (\operatorname {Im} z,\operatorname {Re} z).$ Это соответствует порядку дроби слева направо, записанному $y/x,$ так что $\operatorname {atan2} (y,x)=\operatorname {atan} (y/x)$ для положительных значений $x.$ Однако это противоположно обычному порядку компонентов для комплексных чисел: $z=x+iy,$ или как координаты $(\operatorname {Re} z,\operatorname {Im} z).$ См. раздел Определение и расчет .

Некоторые другие языки программирования (см. § Реализации функции в распространенных компьютерных языках ) вместо этого выбрали противоположный порядок. Например, Microsoft Excel использует $\operatorname {Atan2} (x,y),$ OpenOffice Calc использует $\operatorname {arctan2} (x,y),$ и Mathematica использует $\operatorname {ArcTan} [x,y],$ по умолчанию используется арктангенс с одним аргументом, если вызывается с одним аргументом.

Определение и расчет [ править ]

Функция $atan2$ вычисляет главное значение функции аргумента , примененной к комплексному числу $x + i y$ . То есть $atan2(y, x) = Pr arg(x + i y) = Arg(x + i y)$ . Аргумент можно изменить на произвольное число, кратное $2π$ (что соответствует полному повороту вокруг начала координат), без какого-либо изменения угла, но для однозначного определения $atan2$ используется главное значение в диапазоне $(-\pi ,\pi ]$ , то есть $- π < atan2(y, x) \leq π$ .

С точки зрения стандартной $функции арктанга$ , диапазон которой равен $(-π/2, π/2)$ , ее можно выразить следующим образом, чтобы определить поверхность, которая не имеет разрывов, за исключением полубесконечной линии x<0 y=0:

\operatorname {atan2} (y,x)={\begin{cases}\arctan \left({\frac {y}{x}}\right)&{\text{if }}x>0,\\[5mu]\arctan \left({\frac {y}{x}}\right)+\pi &{\text{if }}x<0{\text{ and }}y\geq 0,\\[5mu]\arctan \left({\frac {y}{x}}\right)-\pi &{\text{if }}x<0{\text{ and }}y<0,\\[5mu]+{\frac {\pi }{2}}&{\text{if }}x=0{\text{ and }}y>0,\\[5mu]-{\frac {\pi }{2}}&{\text{if }}x=0{\text{ and }}y<0,\\[5mu]{\text{undefined}}&{\text{if }}x=0{\text{ and }}y=0.\end{cases}}

Компактное выражение с четырьмя перекрывающимися полуплоскостями:

\operatorname {atan2} (y,x)={\begin{cases}\arctan \left({\frac {y}{x}}\right)&{\text{if }}x>0,\\[5mu]{\frac {\pi }{2}}-{\arctan }{\bigl (}{\frac {x}{y}}{\bigr )}&{\text{if }}y>0,\\[5mu]-{\frac {\pi }{2}}-{\arctan }{\bigl (}{\frac {x}{y}}{\bigr )}&{\text{if }}y<0,\\[5mu]\arctan \left({\frac {y}{x}}\right)\pm \pi &{\text{if }}x<0,\\[5mu]{\text{undefined}}&{\text{if }}x=0{\text{ and }}y=0.\end{cases}}

позволяет Обозначение скобок Айверсона получить еще более компактное выражение: ^{[примечание 1]}

{\begin{aligned}\operatorname {atan2} (y,x)&=\arctan \left({\frac {y}{x}}\right)[x\neq 0]\\[5mu]&\qquad +{\bigl (}1-2[y<0]{\bigr )}\left(\pi [x<0]+{\tfrac {1}{2}}\pi [x=0]\right)\\[5mu]&\qquad +{\text{undefined}}\;\![x=0\wedge y=0]\end{aligned}}

Формула без явной условной конструкции :

\operatorname {atan2} (y,x)=\lim _{z\to x^{+}}\arctan \left({\frac {y}{z}}\right)+{\frac {\pi }{2}}\operatorname {sgn}(y)\operatorname {sgn}(x)\left(\operatorname {sgn}(x)-1\right)

Следующее выражение, полученное из формулы касательного полуугла, также можно использовать для определения $atan2$ :

\operatorname {atan2} (y,x)={\begin{cases}2\arctan \left({\frac {y}{{\sqrt {x^{2}+y^{2}}}+x}}\right)&{\text{if }}x>0{\text{ or }}y\neq 0,\\\pi &{\text{if }}x<0{\text{ and }}y=0,\\{\text{undefined}}&{\text{if }}x=0{\text{ and }}y=0.\end{cases}}

Это выражение может быть более подходящим для символического использования, чем определение, приведенное выше. Однако он непригоден для общего использования в вычислениях с плавающей запятой , так как эффект ошибок округления в

{\textstyle {\sqrt {x^{2}+y^{2}}}}

расширяться вблизи области

x < 0, y = 0

(это может даже привести к делению y на ноль).

Вариант последней формулы, позволяющий избежать завышенных ошибок округления:

\operatorname {atan2} (y,x)={\begin{cases}2\arctan \left({\frac {y}{{\sqrt {x^{2}+y^{2}}}+x}}\right)&{\text{if }}x>0,\\2\arctan \left({\frac {{\sqrt {x^{2}+y^{2}}}-x}{y}}\right)&{\text{if }}x\leq 0{\text{ and }}y\neq 0,\\\pi &{\text{if }}x<0{\text{ and }}y=0,\\{\text{undefined}}&{\text{if }}x=0{\text{ and }}y=0.\end{cases}}

Примечания:

Это дает результаты в диапазоне $(-π, π]$ . ^{[заметка 2]}
Как упоминалось выше, главное значение аргумента $atan2(y, x)$ может быть связано с $arctan(y / x)$ посредством тригонометрии. Вывод происходит следующим образом:
Если $(Икс, у) = (р потому что θ, р грех θ)$ , то $tan(θ /2) = y / (р + x)$ . Следует, что $\operatorname {atan2} (y,x)=\theta =2\,\theta /2=2\arctan {\frac {y}{{\sqrt {x^{2}+y^{2}}}+x}}.$ Обратите внимание, что $\sqrt x 2 + и 2 + x \neq 0$ в рассматриваемой области.

Производная [ править ]

Поскольку функция $atan2$ является функцией двух переменных, она имеет две частные производные . В точках, где эти производные существуют, $atan2$ , за исключением константы, равен $arctan(y / x)$ . Следовательно, для $x > 0$ или $y \neq 0$ ,

{\begin{aligned}&{\frac {\partial }{\partial x}}\operatorname {atan2} (y,\,x)={\frac {\partial }{\partial x}}\arctan \left({\frac {y}{x}}\right)=-{\frac {y}{x^{2}+y^{2}}},\\[5pt]&{\frac {\partial }{\partial y}}\operatorname {atan2} (y,\,x)={\frac {\partial }{\partial y}}\arctan \left({\frac {y}{x}}\right)={\frac {x}{x^{2}+y^{2}}}.\end{aligned}}

Таким образом, градиент atan2 определяется выражением

\nabla {\text{atan2}}(y,x)=\left({-y \over x^{2}+y^{2}},\ {x \over x^{2}+y^{2}}\right).

Неформальное представление функции $atan2$ как угловой функции $θ (x, y) = atan2(y, x)$ (которая определена только с точностью до константы) дает следующую формулу для полного дифференциала :

{\begin{aligned}\mathrm {d} \theta &={\frac {\partial }{\partial x}}\operatorname {atan2} (y,\,x)\,\mathrm {d} x+{\frac {\partial }{\partial y}}\operatorname {atan2} (y,\,x)\,\mathrm {d} y\\[5pt]&=-{\frac {y}{x^{2}+y^{2}}}\,\mathrm {d} x+{\frac {x}{x^{2}+y^{2}}}\,\mathrm {d} y.\end{aligned}}

Хотя функция $atan2$ является разрывной вдоль отрицательной $оси x$ , что отражает тот факт, что угол не может быть определен непрерывно, эта производная определена непрерывно, за исключением начала координат, что отражает тот факт, что бесконечно малые (и даже локальные) изменения угла могут быть определены везде. кроме происхождения. Интегрирование этой производной по пути дает общее изменение угла по пути, а интегрирование по замкнутому контуру дает число витков .

На языке дифференциальной геометрии эта производная есть одноформа , причем она замкнута (ее производная равна нулю), но не точна (она не является производной 0-формы, т. е. функцией), и фактически она порождает первые когомологии де Рама плоскости проколотой . Это самый простой пример такой формы, и он является фундаментальным в дифференциальной геометрии.

Частные производные $atan2$ не содержат тригонометрических функций, что делает их особенно полезными во многих приложениях (например, встроенных системах), где вычисление тригонометрических функций может оказаться дорогостоящим.

Иллюстрации [ править ]

На этом рисунке показаны значения atan2 вдоль выбранных лучей от начала координат, отмеченных единичным кругом. Значения в радианах показаны внутри круга. В диаграмме используется стандартное математическое соглашение, согласно которому углы увеличиваются против часовой стрелки от нуля вдоль луча вправо. Обратите внимание, что порядок аргументов обратный; функция $atan2(y, x)$ вычисляет угол, соответствующий точке $(x, y)$ .

На этом рисунке показаны значения $\arctan(\tan(\theta ))$ вместе с $\operatorname {atan2} (\sin(\theta ),\cos(\theta ))$ для $0\leq \theta \leq 2\pi$ . Обе функции нечетные и периодические с периодами $\pi$ и $2\pi$ соответственно, и, таким образом, может быть легко дополнено к любой области реальных значений $\theta$ . Хорошо видны ветвей срезы $\operatorname {atan2}$ -функция в $\theta =\pi$ и $\arctan$ -функция в $\theta \in \{{\tfrac {\pi }{2}},\;{\tfrac {3\pi }{2}}\}$ . ^[3]

На двух рисунках ниже показаны 3D-изображения соответственно $atan2(y, x)$ и $arctan( .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}y / x )$ над областью плоскости. Обратите внимание, что для $atan2(y, x)$ -плоскости , лучи в X / Y исходящие из начала координат, имеют постоянные значения, а для $arctan(y / x)$ линии в X / Y -плоскости, проходящие через начало координат, имеют постоянные значения. При $x > 0$ две диаграммы дают одинаковые значения.

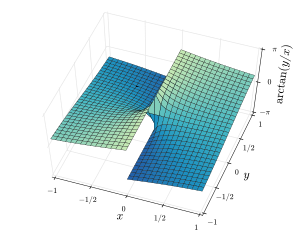Тождество суммы и разности углов [ править ]

Сумма или разность нескольких углов, вычисляемая по формуле $\operatorname {atan2}$ альтернативно могут быть вычислены путем составления их как комплексных чисел . Учитывая две пары координат $(x_{1},y_{1})$ и $(x_{2},y_{2})$ , их углы от положительных $x$ оси будут составлены (и длины умножены), если они рассматриваются как комплексные числа, а затем умножаются вместе, $(x_{1}+iy_{1})(x_{2}+iy_{2})={}$ $(x_{1}x_{2}-y_{1}y_{2})+i(y_{1}x_{2}+x_{1}y_{2})$ . Полученный угол можно найти с помощью одного $\operatorname {atan2}$ операции, пока результирующий угол лежит в $(-\pi ,\pi ]$ :

\operatorname {atan2} (y_{1},x_{1})\pm \operatorname {atan2} (y_{2},x_{2})=\operatorname {atan2} (y_{1}x_{2}\pm x_{1}y_{2},x_{1}x_{2}\mp y_{1}y_{2}),

и аналогично для более чем двух пар координат. Если составленный угол пересекает отрицательный $x$ -ось (т.е. выходит за пределы диапазона $(-\pi ,\pi ]$ ), то пересечения можно посчитать и найти соответствующее целое число, кратное $2\pi$ добавлено к окончательному результату, чтобы исправить его.

Эта разностная формула часто используется на практике для вычисления угла между двумя плоскими векторами , поскольку результирующий угол всегда находится в диапазоне $(-\pi ,\pi ]$ .

восток против часовой стрелки, север часовой стрелки, юг часовой стрелки и т. д. Условные обозначения :

The $\mathrm {atan2}$ Функция изначально была разработана для соглашения в чистой математике, которое можно назвать восток-против часовой стрелки . Однако в практических приложениях по северной и южной часовой стрелке часто нормой являются соглашения . Например, в науках об атмосфере направление ветра можно рассчитать с помощью $\mathrm {atan2}$ функция с восточным и северным компонентами вектора ветра в качестве аргументов; ^[4] можно Угол азимута Солнца рассчитать аналогичным образом, используя в качестве аргументов восточную и северную компоненты солнечного вектора. Направление ветра обычно определяется по направлению на север по часовой стрелке, а угол азимута Солнца широко использует соглашения как по северной, так и по южной часовой стрелке. ^[5] Эти различные соглашения можно реализовать, поменяв местами позиции и изменив знаки аргументов x и y следующим образом:

$\mathrm {atan2} (y,x),\;\;\;\;\;$ (Восточная конвенция против часовой стрелки)
$\mathrm {atan2} (x,y),\;\;\;\;\;$ (Конвенция по северной часовой стрелке)
$\mathrm {atan2} (-x,-y)$ . (Конвенция по южной часовой стрелке)

В качестве примера позвольте $x_{0}={\frac {\sqrt {3}}{2}}$ и $y_{0}={\frac {1}{2}}$ , то формат восток-против часовой стрелки дает $\mathrm {atan2} (y_{0},x_{0})\cdot {\frac {180}{\pi }}=30^{\circ }$ , формат по северной часовой стрелке дает $\mathrm {atan2} (x_{0},y_{0})\cdot {\frac {180}{\pi }}=60^{\circ }$ , а формат по южной часовой стрелке дает $\mathrm {atan2} (-x_{0},-y_{0})\cdot {\frac {180}{\pi }}=-120^{\circ }$ .

Изменение знака аргументов x и/или y и/или замена их позиций может создать 8 возможных вариантов $\mathrm {atan2}$ функции и они, что интересно, соответствуют 8 возможным определениям угла, а именно, по часовой стрелке или против часовой стрелки, начиная с каждого из 4 сторон света : севера, востока, юга и запада.

функции на распространенных языках Реализации компьютерных

Реализация функции отличается от одного компьютерного языка к другому:

В Microsoft Excel , ^[6] OpenOffice.org Calc , LibreOffice Calc , ^[7] таблицы Google , ^[8] и номера iWork , ^[9] функция арктангенса с двумя аргументами имеет два аргумента в стандартной последовательности $(\operatorname {Re} ,\operatorname {Im} )$ (перевернуто по сравнению с соглашением, использованным в обсуждении выше).
В системе Mathematica форма ArcTan[x, y]используется там, где форма с одним параметром предоставляет нормальный арктангенс. Система Mathematica классифицирует ArcTan[0, 0] как неопределенное выражение.
На большинстве графических калькуляторов TI (за исключением TI-85 и TI-86 ) эквивалентная функция называется R►Pθ и имеет аргументы $(\operatorname {Re} ,\operatorname {Im} )$ .
В TI-85 $функция arg$ называется angle(x,y) и хотя кажется, что он принимает два аргумента, на самом деле у него есть только один комплексный аргумент, который обозначается парой чисел: $x + i y = (x, y)$ .

The $(\operatorname {Im} ,\operatorname {Re} )$ соглашение используется:

Функция С atan2и большинство других компьютерных реализаций предназначены для уменьшения усилий по преобразованию декартовых координат в полярные и поэтому всегда определяют atan2(0, 0). В реализациях без знакового нуля или при наличии положительных нулевых аргументов он обычно определяется как 0. Он всегда будет возвращать значение в диапазоне $[-π, π]$ , а не вызывать ошибку или возвращать NaN (не число).
В Common Lisp , где существуют необязательные аргументы, atan функция позволяет опционально указать координату x : (atan y x). ^[10]
В Julia ситуация аналогична Common Lisp: вместо atan2, язык имеет однопараметрическую и двухпараметрическую форму для atan. ^[11] Однако у него гораздо больше двух методов, позволяющих проводить агрессивную оптимизацию во время компиляции (см. раздел «Почему бы вам не скомпилировать код Matlab/Python/R/… в Julia?» ^[12]).
Для систем, реализующих знаковый ноль , бесконечность или Not a Number (например, IEEE с плавающей запятой ), обычно реализуются разумные расширения, которые могут расширить диапазон создаваемых значений, включив в него − $π$ и −0, когда $y$ = −0. Они также могут возвращать NaN или вызывать исключение при получении аргумента NaN.
В архитектуры Intel x86 ассемблерном коде : atan2 известен как FPATAN (частичный арктангенс с плавающей запятой). ^[13] Он может иметь дело с бесконечностями, и результаты лежат в замкнутом интервале $[-π, π]$ , например atan2(∞, x)= + $π$ /2 для конечного x . Особенно, FPATAN определяется, когда оба аргумента равны нулю:
atan2(+0, +0) = +0;

atan2(+0, −0) = + $π$ ;

atan2(−0, +0) = −0;

atan2(−0, −0) знак равно - $π$ .

Это определение связано с понятием знакового нуля .

В математических трудах, кроме исходного кода, например, в книгах и статьях, обозначения Arctan ^[14] и Тан ⁻¹^[15]были использованы; это варианты обычного арктана и коричневого с заглавной буквы. ⁻¹. Такое использование согласуется с обозначением комплексного аргумента , например, $Atan(y, x) = Arg(x + i y)$ .
В калькуляторах HP рассматривайте координаты как комплексное число, а затем принимайте ARG. Или << C->R ARG >> 'ATAN2' STO.
В научных калькуляторах функцию часто можно рассчитать как угол, полученный при $(x, y)$ преобразовании из прямоугольных координат в полярные координаты .
Системы, поддерживающие символьную математику, обычно возвращают неопределенное значение для $atan2(0, 0)$ или иным образом сигнализируют о возникновении ненормального состояния.
Бесплатная математическая библиотека FDLIBM (Свободно распространяемая LIBM), доступная на сайте netlib, имеет исходный код, показывающий, как она реализуется. atan2 включая обработку различных исключительных значений IEEE.
Для систем без аппаратного умножителя функция $atan2$ может быть реализована численно надежным способом с помощью метода CORDIC . Таким образом, реализации $atan(y)$ , вероятно, предпочтут вычислить $atan2(y, 1)$ .

См. также [ править ]

гипотеза

Ссылки [ править ]

^ «Аргумент комплексного числа» (PDF) . Институт физики элементарных частиц Санта-Крус. Зима 2011.
^ Органик, Эллиот И. (1966). Букварь по Фортрану IV . Аддисон-Уэсли. п. 42. Некоторые процессоры также предлагают библиотечную функцию ATAN2, функцию двух аргументов (противоположного и соседнего).
^ «Вольф Юнг: Мандель, программное обеспечение для сложной динамики» . www.mndynamics.com . Проверено 20 апреля 2018 г.
^ «Краткий справочник по направлению ветра» . Лаборатория наблюдения Земли NCAR UCAR.
^ Чжан, Тайпин; Стэкхаус, Пол В.; Макферсон, Брэдли; Миковиц, Дж. Коллин (2021). «Формула солнечного азимута, которая делает ненужным подробное рассмотрение без ущерба для математической строгости: математическая установка, применение и расширение формулы, основанной на подсолнечной точке и функции atan2» . Возобновляемая энергия . 172 : 1333–1340. doi : 10.1016/j.renene.2021.03.047 . S2CID 233631040 .
^ «Метод Microsoft Excel Atan2» . Майкрософт.
^ «LibreOffice Calc ATAN2» . LibreOffice.org.
^ «Функции и формулы – Помощь редакторам документации» . support.google.com .
^ «Список тригонометрических функций чисел» . Яблоко.
^ «CLHS: Функция ASIN, ACOS, ATAN» . Лиспворкс.
^ «Математика · Язык Джулии» . docs.julialang.org .
^ «Часто задаваемые вопросы · Язык Джулии» . docs.julialang.org .
^ IA-32 Руководство разработчика программного обеспечения для архитектуры Intel. Том 2A: Справочник по набору команд, AM, 2004 г.
^ Бургер, Вильгельм; Бердж, Марк Дж. (7 июля 2010 г.). Принципы цифровой обработки изображений: фундаментальные методы . Springer Science & Business Media. ISBN 978-1-84800-191-6 . Проверено 20 апреля 2018 г. - через Google Книги.
^ Глиссон, Тилдон Х. (18 февраля 2011 г.). Введение в анализ и проектирование цепей . Springer Science & Business Media. ISBN 9789048194438 . Проверено 20 апреля 2018 г. - через Google Книги.

Внешние ссылки [ править ]

Другие реализации/код для atan2

«Перинг между двумя точками» . Архивировано из оригинала 18 ноября 2020 года . Проверено 21 февраля 2022 г.

«Арктан и полярные координаты» . Архивировано из оригинала 18 октября 2018 года . Проверено 21 февраля 2022 г.

«Что такое «Арккос»?» . Архивировано из оригинала 6 сентября 2017 года . Проверено 21 февраля 2022 г.

Примечания [ править ]

^ Предполагая определения ${\text{undefined}}\cdot 0=0,$ ${\text{undefined}}\cdot 1={\text{undefined}},$ и $z+{\text{undefined}}={\text{undefined}}$ для любого $z.$
^ Можно применить периодичность результата для сопоставления с другим желаемым диапазоном, например, сопоставления с $[0, 2π),$ добавив $2π$ к отрицательным результатам.

[1] «Аргумент комплексного числа» (PDF) . Институт физики элементарных частиц Санта-Крус. Зима 2011.

[2] Органик, Эллиот И. (1966). Букварь по Фортрану IV . Аддисон-Уэсли. п. 42. Некоторые процессоры также предлагают библиотечную функцию ATAN2, функцию двух аргументов (противоположного и соседнего).

[5] «Вольф Юнг: Мандель, программное обеспечение для сложной динамики» . www.mndynamics.com . Проверено 20 апреля 2018 г.

[6] «Краткий справочник по направлению ветра» . Лаборатория наблюдения Земли NCAR UCAR.

[7] Чжан, Тайпин; Стэкхаус, Пол В.; Макферсон, Брэдли; Миковиц, Дж. Коллин (2021). «Формула солнечного азимута, которая делает ненужным подробное рассмотрение без ущерба для математической строгости: математическая установка, применение и расширение формулы, основанной на подсолнечной точке и функции atan2» . Возобновляемая энергия . 172 : 1333–1340. doi : 10.1016/j.renene.2021.03.047 . S2CID 233631040 .

[8] «Метод Microsoft Excel Atan2» . Майкрософт.

[9] «LibreOffice Calc ATAN2» . LibreOffice.org.

[10] «Функции и формулы – Помощь редакторам документации» . support.google.com .

[11] «Список тригонометрических функций чисел» . Яблоко.

[12] «CLHS: Функция ASIN, ACOS, ATAN» . Лиспворкс.

[13] «Математика · Язык Джулии» . docs.julialang.org .

[14] «Часто задаваемые вопросы · Язык Джулии» . docs.julialang.org .

[15] IA-32 Руководство разработчика программного обеспечения для архитектуры Intel. Том 2A: Справочник по набору команд, AM, 2004 г.

[16] Бургер, Вильгельм; Бердж, Марк Дж. (7 июля 2010 г.). Принципы цифровой обработки изображений: фундаментальные методы . Springer Science & Business Media. ISBN 978-1-84800-191-6 . Проверено 20 апреля 2018 г. - через Google Книги.

[17] Глиссон, Тилдон Х. (18 февраля 2011 г.). Введение в анализ и проектирование цепей . Springer Science & Business Media. ISBN 9789048194438 . Проверено 20 апреля 2018 г. - через Google Книги.

[3] Предполагая определения ${\text{undefined}}\cdot 0=0,$ ${\text{undefined}}\cdot 1={\text{undefined}},$ и $z+{\text{undefined}}={\text{undefined}}$ для любого $z.$

[4] Можно применить периодичность результата для сопоставления с другим желаемым диапазоном, например, сопоставления с $[0, 2π),$ добавив $2π$ к отрицательным результатам.

[1]

[2]

[примечание 1]

[заметка 2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

v т Это Тригонометрические и гиперболические функции
Группы	Тригонометрический Синус и косинус Обратная тригонометрическая гиперболический Обратная гиперболическая
Другой	Его версия Дайте им высохнуть Джья, коти-джья и уткрама-джья Атан2