Delta- v

Дельта- » ) , обозначаемая v (более известная как «изменение скорости как ${\textstyle {\Delta v}}$ и выраженная дельта-ви , используемая в динамике полета космического корабля , является мерой импульса на единицу массы космического корабля, который необходим для выполнения маневра, такого как запуск или приземление на планету или луну, или орбитальный маневр в космосе. . Это скаляр , имеющий единицы скорости . В данном контексте это не то же самое, что физическое изменение скорости космического корабля.

Простым примером может служить обычный космический корабль с ракетным двигателем, тяга которого достигается за счет сжигания топлива. такого космического корабля Тогда дельта- v будет представлять собой изменение скорости, которого космический корабль может достичь, сжигая весь запас топлива.

Дельта- v создается реактивными двигателями , такими как ракетные двигатели , и пропорциональна тяге на единицу массы и времени горения. Он используется для определения массы топлива, необходимой для данного маневра, посредством уравнения ракеты Циолковского .

Для нескольких маневров дельта- v суммируется линейно.

Для межпланетных миссий дельта- v часто отображается на графике , который отображает требуемую дельту- v миссии как функцию даты запуска.

Определение

$\Delta {v}=\int _{t_{0}}^{t_{1}}{\frac {|T(t)|}{m(t)}}\,dt$ где

$T (t)$ — мгновенная тяга в момент времени $t$ .
$m (t)$ — мгновенная масса в момент времени $t$ .

Конкретные случаи

При отсутствии внешних сил: $\Delta {v}=\int _{t_{0}}^{t_{1}}\left|{\dot {v}}\right|\,dt$ где ${\dot {v}}$ - координатное ускорение.

Когда тяга приложена в постоянном направлении ( $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ в / | в | ⁠$ является константой), это упрощается до: $\Delta {v}=|v_{1}-v_{0}|$ это просто величина изменения скорости . Однако в общем случае это соотношение не выполняется: если, например, постоянное однонаправленное ускорение меняется на противоположное после $(t 1 - t 0)/2$ , то разность скоростей равна 0, но дельта- v такая же, как и для нереверсивная тяга.

Для ракет под «отсутствием внешних сил» понимают отсутствие силы тяжести и сопротивления атмосферы, а также отсутствие аэростатического противодавления на сопло, поэтому вакуум I _sp. аппарата используется для расчета дельта - вместимости через уравнение ракеты . затраты на атмосферные потери и гравитационное сопротивление . добавляются в дельта - бюджет Кроме того, при запусках с поверхности планеты ^[1]

Орбитальные маневры

Орбитальные маневры выполняются путем запуска двигателя для создания силы реакции, действующей на космический корабль. Размер этой силы будет

T=v_{\text{exh}}\ \rho

( 1 )

где

$v exh$ — скорость выхлопных газов в корпусе ракеты.
$ρ$ — расход топлива в камеру сгорания.

Ускорение ${\dot {v}}$ космического корабля, вызванная этой силой, будет

{\dot {v}}={\frac {T}{m}}=v_{\text{exh}}\ {\frac {\rho }{m}}

( 2 )

где $m$ - масса космического корабля

В процессе горения масса космического корабля уменьшится за счет использования топлива, причем производная массы по времени равна

{\dot {m}}=-\rho \,

( 3 )

Если теперь направление силы, т. е. направление сопла , фиксировано во время горения, мы получим увеличение скорости от силы двигателя горения, начиная с момента времени $t_{0}\,$ и заканчивающийся в момент $t 1$ как

\Delta {v}=-\int _{t_{0}}^{t_{1}}{v_{\text{exh}}\ {\frac {\dot {m}}{m}}}\,dt

( 4 )

Меняя переменную интегрирования с момента времени $t$ на массу космического корабля $m,$ получим

\Delta {v}=-\int _{m_{0}}^{m_{1}}{v_{\text{exh}}\ {\frac {dm}{m}}}

( 5 )

Предполагая $v_{\text{exh}}\,$ быть константой, не зависящей от количества оставшегося топлива, это соотношение интегрируется в

\Delta {v}=v_{\text{exh}}\ \ln \left({\frac {m_{0}}{m_{1}}}\right)

( 6 )

что представляет собой уравнение ракеты Циолковского .

Если, например, 20% стартовой массы составляет топливо, что дает постоянную $v_{\text{exh}}$ 2100 м/с (типовое значение для гидразинового двигателя) мощность системы управления реакцией составляет $\Delta {v}=2100\ \ln \left({\frac {1}{0.8}}\right)\,{\text{m/s}}=460\,{\text{m/s}}.$

Если $v_{\text{exh}}$ является непостоянной функцией количества оставшегося топлива. ^[2] $v_{\text{exh}}=v_{\text{exh}}(m)$ мощность системы управления реакцией вычисляется по интегралу ( 5 ).

Ускорение ( 2 ), вызванное силой двигателя, представляет собой просто дополнительное ускорение, которое следует добавить к другим ускорениям (сила на единицу массы), воздействующим на космический корабль, и его орбиту можно легко распространить с помощью численного алгоритма, включив также эту силу двигателя. ^[3] Но для многих целей, обычно для исследований или оптимизации маневров, они аппроксимируются импульсными маневрами, как показано на рисунке 1, с $\Delta {v}$ как указано в ( 4 ). Подобным образом можно, например, использовать подход «исправленных коник», моделирующий маневр как переход с одной орбиты Кеплера на другую путем мгновенного изменения вектора скорости.

Это приближение к импульсивным маневрам в большинстве случаев очень точное, по крайней мере, когда используется химическое движение. Для систем с малой тягой, обычно электрических двигательных установок, это приближение менее точно. Но даже для геостационарных космических аппаратов, использующих электрическую двигательную установку для управления вне плоскости с периодами работы двигателей, продолжающимися несколько часов вокруг узлов, это приближение справедливо.

Производство

Дельта- v обычно обеспечивается тягой ракетного двигателя , но может создаваться и другими двигателями. Скорость изменения delta- v во времени представляет собой величину ускорения, вызываемого двигателями , т. е. тягу на общую массу транспортного средства. Фактический вектор ускорения можно найти путем добавления тяги на массу к вектору силы тяжести и векторам, представляющим любые другие силы, действующие на объект.

Общая необходимая разница является хорошей отправной точкой для принятия ранних проектных решений, поскольку рассмотрение дополнительных сложностей откладывается на более поздние этапы процесса проектирования.

Уравнение ракеты показывает, что требуемое количество топлива резко возрастает с увеличением delta- v . Поэтому в современных двигательных системах космических кораблей значительные исследования проводятся по уменьшению общей дельта- волны, необходимой для данного космического полета, а также по проектированию космических аппаратов, способных создавать большую дельту- волну .

Увеличение дельта- v, обеспечиваемое двигательной установкой, может быть достигнуто за счет:

Несколько маневров

Поскольку соотношения масс применимы к любому данному ожогу, при последовательном выполнении нескольких маневров соотношения масс умножаются.

Таким образом, можно показать, что при условии фиксированной скорости истечения это означает, что дельту- v можно суммировать:

Когда $m 1, m 2$ — соотношения масс маневров, а $v 1, v 2$ — дельта -v первого и второго маневров. ${\begin{aligned}m_{1}m_{2}&=e^{V_{1}/V_{e}}e^{V_{2}/V_{e}}\\&=e^{\frac {V_{1}+V_{2}}{V_{e}}}\\&=e^{V/V_{e}}=M\end{aligned}}$ где $V знак равно v 1 + v 2$ и $M знак равно м 1 м 2$ . Это просто уравнение ракеты, примененное к сумме двух маневров.

Это удобно, поскольку означает, что дельту- v можно вычислить и просто сложить, а соотношение масс рассчитать только для всего транспортного средства за всю миссию. Таким образом, обычно указывается дельта- v, а не отношения масс, которые требуют умножения.

Delta- v budgets

При проектировании траектории бюджет delta- v используется как хороший индикатор того, сколько топлива потребуется. Расход топлива является экспоненциальной функцией delta- v в соответствии с уравнением ракеты , он также будет зависеть от скорости истечения.

Невозможно определить к дельта- v требования из сохранения энергии , рассматривая только полную энергию транспортного средства на начальной и конечной орбитах, поскольку энергия уносится с выхлопными газами (см. также ниже). Например, большинство космических аппаратов запускаются на орбиту с наклоном, довольно близким к широте стартовой площадки, чтобы использовать преимущества скорости вращения поверхности Земли. Если по задачам миссии необходимо вывести космический корабль на орбиту различного наклонения существенная дельта- v , требуется , хотя удельная кинетическая и потенциальная энергии на конечной и начальной орбитах равны.

Когда тяга ракеты применяется короткими импульсами, другие источники ускорения могут быть незначительными, и величина изменения скорости одного взрыва может быть просто аппроксимирована дельта- v . Общая дельта- v, которую необходимо применить, затем может быть просто определена путем сложения каждой из дельта- v, необходимых для дискретных включений, даже если между всплесками величина и направление скорости изменяются под действием силы тяжести, например, в эллиптической орбита .

Примеры расчета дельта- v см. в разделах «Переходная орбита Гомана» , «Гравитационная рогатка » и «Межпланетная транспортная сеть» . Также примечательно, что большая тяга может уменьшить гравитационное сопротивление .

Дельта- v также необходим для удержания спутников на орбите и расходуется на маневры по поддержанию орбитальной станции . Поскольку запас топлива на большинстве спутников не может быть пополнен, количество топлива, первоначально загруженного на спутник, вполне может определять его полезный срок службы.

Эффект Оберта

Из соображений мощности оказывается, что при приложении delta- v в направлении скорости удельная орбитальная энергия, получаемая на единицу delta- v, равна мгновенной скорости. Это называется эффектом Оберта.

Например, спутник на эллиптической орбите более эффективно разгоняется на высокой скорости (то есть на небольшой высоте), чем на низкой скорости (то есть на большой высоте).

Другой пример: когда транспортное средство пролетает над планетой, сжигание топлива при максимальном приближении, а не при удалении от него, дает значительно более высокую конечную скорость, и это тем более верно, когда планета большая с глубоким гравитационным полем. например Юпитер.

См. также активные рогатки .

Сюжет со свининой

Из-за того, что относительное положение планет меняется с течением времени, в разные даты запуска требуются разные дельта-v. Диаграмму, показывающую требуемую дельту- v в зависимости от времени, иногда называют графиком свиной отбивной . Такая диаграмма полезна, поскольку она позволяет рассчитать окно запуска , поскольку запуск должен происходить только тогда, когда миссия находится в пределах возможностей используемой машины. ^[4]

Вокруг Солнечной системы

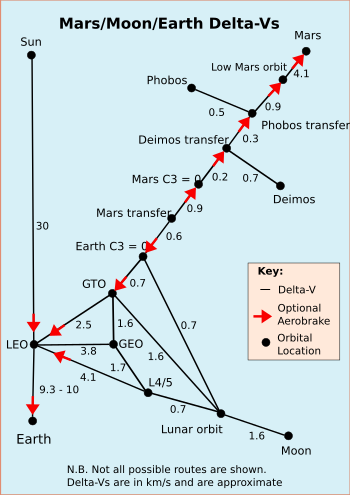
Дельта-v необходима для различных орбитальных маневров с использованием обычных ракет; красные стрелки показывают, где дополнительное аэроторможение , черные цифры обозначают дельту-v в км/с, применимую в любом направлении. в этом конкретном направлении можно выполнить ^[5]^[6] Передачи с более низкой дельтой v, чем показано, часто могут быть достигнуты, но они включают редкие окна передачи или занимают значительно больше времени, см.: Нечеткие орбитальные передачи .

С3: Покинуть орбиту
ГЕО: Геосинхронная орбита
ГТО: Геостационарная переходная орбита
Л4/5: Земля–Луна L ₄ L ₅ точка Лагранжа
ЛЕО: Низкая околоземная орбита

возвращение в атмосферу НОО

Например, космический корабль «Союз» сходит с орбиты МКС в два этапа. Во-первых, для безопасного отделения от космической станции ему необходима дельта-v 2,18 м/с. ему потребуется еще 128 м/с Затем для входа в атмосферу . ^[7]

См. также

Ссылки

^ Сарыгуль-Кляйн, Несрин; Ноэль, Крис; Саригул-Клин, Мартинус (5 января 2004 г.). Транспортные средства с воздушным запуском на орбиту: Delta V выигрывает от условий запуска и аэродинамики транспортного средства . дои : 10.2514/6.2004-872 . ISBN 9781624100789 .
^ Может иметь место система «продувки», в которой давление в баке падает после использования топлива, и это не только расход топлива. $\rho$ но в несколько меньшей степени и скорость истечения $v_{\text{exh}}$ уменьшается.
^ Сила тяги на единицу массы составляет ${\frac {f(t)}{m(t)}}=v_{\text{exh}}(t){\frac {{\dot {m}}(t)}{m(t)}}$ где $f(t)$ и $m(t)$ заданы функции времени $t$ .
^ «Освоение Марса: Особенности» . marsprogram.jpl.nasa.gov .
^ «Ракеты и космический транспорт» . Архивировано из оригинала 1 июля 2007 года . Проверено 1 июня 2013 г.
^ «Калькулятор Дельта-V» . Архивировано из оригинала 12 марта 2000 года. Дает цифры 8,6 от поверхности Земли до LEO, 4,1 и 3,8 для LEO до лунной орбиты (или L5) и GEO соответственно, 0,7 для L5 до лунной орбиты и 2,2 для лунной орбиты до лунной орбиты. лунная поверхность. Говорят, что цифры взяты из главы 2 книги « Космические поселения: исследование дизайна», заархивированной 28 ноября 2001 г. в веб-архивах Библиотеки Конгресса на веб-сайте НАСА. ^{[ мертвая ссылка ]}.
^ Гебхардт, Крис (17 апреля 2021 г.). «Союз МС-17 благополучно возвращает в Казахстан трех членов экипажа станции» . nasaspaceflight.com . Проверено 10 июля 2022 г.

[1] Сарыгуль-Кляйн, Несрин; Ноэль, Крис; Саригул-Клин, Мартинус (5 января 2004 г.). Транспортные средства с воздушным запуском на орбиту: Delta V выигрывает от условий запуска и аэродинамики транспортного средства . дои : 10.2514/6.2004-872 . ISBN 9781624100789 .

[2] Может иметь место система «продувки», в которой давление в баке падает после использования топлива, и это не только расход топлива. $\rho$ но в несколько меньшей степени и скорость истечения $v_{\text{exh}}$ уменьшается.

[3] Сила тяги на единицу массы составляет ${\frac {f(t)}{m(t)}}=v_{\text{exh}}(t){\frac {{\dot {m}}(t)}{m(t)}}$ где $f(t)$ и $m(t)$ заданы функции времени $t$ .

[4] «Освоение Марса: Особенности» . marsprogram.jpl.nasa.gov .

[marsdeltavs-5] «Ракеты и космический транспорт» . Архивировано из оригинала 1 июля 2007 года . Проверено 1 июня 2013 г.

[6] «Калькулятор Дельта-V» . Архивировано из оригинала 12 марта 2000 года. Дает цифры 8,6 от поверхности Земли до LEO, 4,1 и 3,8 для LEO до лунной орбиты (или L5) и GEO соответственно, 0,7 для L5 до лунной орбиты и 2,2 для лунной орбиты до лунной орбиты. лунная поверхность. Говорят, что цифры взяты из главы 2 книги « Космические поселения: исследование дизайна», заархивированной 28 ноября 2001 г. в веб-архивах Библиотеки Конгресса на веб-сайте НАСА. ^{[ мертвая ссылка ]}.

[Soyuz_returns-7] Гебхардт, Крис (17 апреля 2021 г.). «Союз МС-17 благополучно возвращает в Казахстан трех членов экипажа станции» . nasaspaceflight.com . Проверено 10 июля 2022 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]