Орбитальная механика

Спутник, вращающийся вокруг Земли, имеет тангенциальную скорость и внутреннее ускорение .

Орбитальная механика или астродинамика — применение баллистики и небесной механики к практическим задачам движения ракет , спутников и других космических аппаратов . Движение этих объектов обычно рассчитывается на основе законов движения Ньютона и закона всемирного тяготения . Орбитальная механика является основной дисциплиной при проектировании и управлении космическими миссиями .

Небесная механика в более широком смысле рассматривает орбитальную динамику систем, находящихся под влиянием гравитации , включая как космические корабли, так и естественные астрономические тела, такие как звездные системы , планеты , луны и кометы . Орбитальная механика фокусируется на траекториях космических кораблей , включая орбитальные маневры , смену орбитальных плоскостей и межпланетные перемещения, и используется планировщиками миссий для прогнозирования результатов двигательных маневров .

Общая теория относительности является более точной теорией для расчета орбит, чем законы Ньютона, и иногда ее необходимо использовать для большей точности или в ситуациях с высокой гравитацией (например, при орбитах вблизи Солнца).

История

До появления космических путешествий в двадцатом веке не было большого различия между орбитальной и небесной механикой. Во времена «Спутника » эту область называли «космической динамикой». Таким образом, фундаментальные методы, такие как те, которые используются для решения проблемы Кеплера (определение положения как функции времени), одинаковы в обеих областях. Более того, история полей почти полностью общая.

Иоганн Кеплер был первым, кто успешно смоделировал орбиты планет с высокой степенью точности, опубликовав свои законы в 1605 году. Исаак Ньютон опубликовал более общие законы небесного движения в первом издании Philosophiæ Naturalis Principia Mathematica (1687), в котором был предложен метод нахождение орбиты тела, следующего по параболической траектории, по трем наблюдениям. Это использовалось Эдмундом Галлеем для установления орбит различных комет, в том числе и той, которая носит его имя . Метод последовательного приближения Ньютона был формализован в аналитический метод Леонардом Эйлером в 1744 году, чьи работы, в свою очередь, были обобщены на эллиптические и гиперболические орбиты Иоганном Ламбертом в 1761–1777 годах.

Еще одной вехой в определении орбиты стала помощь Карла Фридриха Гаусса в «восстановлении» карликовой планеты Церера в 1801 году. Метод Гаусса смог использовать всего три наблюдения (в виде пар прямого восхождения и склонения ), чтобы найти шесть орбитальных элементов , полностью описывающих орбиту. Теория определения орбиты впоследствии была развита до такой степени, что сегодня она применяется в GPS-приемниках, а также для отслеживания и каталогизации вновь наблюдаемых малых планет . Современное определение и прогнозирование орбит используются для эксплуатации всех типов спутников и космических зондов, поскольку необходимо знать их будущее положение с высокой степенью точности.

Астродинамика была разработана астрономом Сэмюэлем Херриком в 1930-х годах. Он проконсультировался с ученым-ракетчиком Робертом Годдардом, и ему было предложено продолжить работу над методами космической навигации, поскольку Годдард считал, что они понадобятся в будущем. Численные методы астродинамики были объединены с новыми мощными компьютерами в 1960-х годах, и люди были готовы отправиться на Луну и вернуться.

Практические приемы

Дополнительная информация: Список орбит.

Практические правила

Следующие практические правила полезны для ситуаций, аппроксимируемых классической механикой при стандартных предположениях астродинамики, изложенных ниже. Обсуждаемый конкретный пример касается спутника, вращающегося вокруг планеты, но практические правила могут быть применимы и к другим ситуациям, например, к орбитам небольших тел вокруг звезды, такой как Солнце.

• Законы движения планет Кеплера :
  • Орбиты эллиптические , с более тяжелым телом в одном из фокусов эллипса. Особым случаем является круговая орбита (круг — частный случай эллипса) с планетой в центре.
  • Линия, проведенная от планеты к спутнику, охватывает равные площади за одинаковое время, независимо от того, какой участок орбиты измеряется.
  • Квадрат орбитального периода спутника пропорционален кубу его среднего расстояния от планеты.
• Без приложения силы (например, запуска ракетного двигателя) период и форма орбиты спутника не изменятся.
• Спутник на низкой орбите (или низкой части эллиптической орбиты) движется относительно поверхности планеты быстрее, чем спутник на более высокой орбите (или высокой части эллиптической орбиты), из-за более сильного гравитационного поля. притяжение ближе к планете.
• Если тяга приложена только в одной точке орбиты спутника, он будет возвращаться в эту же точку на каждой последующей орбите, хотя остальная часть его пути изменится. Таким образом, невозможно перейти с одной круговой орбиты на другую с помощью лишь одного кратковременного приложения тяги.
• С круговой орбиты тяга, приложенная в направлении, противоположном движению спутника, меняет орбиту на эллиптическую; спутник спустится и достигнет самой низкой точки орбиты ( периапсы ) на расстоянии 180 градусов от огневой точки; тогда оно поднимется обратно. Период результирующей орбиты будет меньше периода исходной круговой орбиты. Тяга, приложенная в направлении движения спутника, создает эллиптическую орбиту с самой высокой точкой ( апоапсе ) на расстоянии 180 градусов от точки стрельбы. Период результирующей орбиты будет больше, чем период исходной круговой орбиты.

Последствия правил орбитальной механики иногда противоречат здравому смыслу. Например, если два космических корабля находятся на одной круговой орбите и желают состыковаться, если только они не находятся очень близко, идущий за ними корабль не сможет просто запустить свои двигатели, чтобы двигаться быстрее. Это изменит форму его орбиты, заставив его набрать высоту и фактически замедлиться относительно ведущего корабля, не достигнув цели. Космическое сближение перед стыковкой обычно требует нескольких точно рассчитанных запусков двигателей в течение нескольких орбитальных периодов, на завершение которых требуются часы или даже дни.

В той степени, в которой стандартные предположения астродинамики не верны, реальные траектории будут отличаться от рассчитанных. Например, простое сопротивление атмосферы является еще одним усложняющим фактором для объектов на низкой околоземной орбите .

Эти эмпирические правила явно неточны при описании двух или более тел одинаковой массы, таких как двойная звездная система (см. Задача n тел ). Небесная механика использует более общие правила, применимые к более широкому кругу ситуаций. Законы движения планет Кеплера, которые могут быть математически выведены из законов Ньютона, строго справедливы только при описании движения двух гравитирующих тел в отсутствие негравитационных сил; они также описывают параболические и гиперболические траектории. В непосредственной близости от крупных объектов, таких как звезды, также становятся важными различия между классической механикой и общей теорией относительности .

Законы астродинамики

См. Также: вектор Лапласа – Рунге – Ленца.

Фундаментальными законами астродинамики являются закон всемирного тяготения Ньютона и законы движения Ньютона , а фундаментальным математическим инструментом является дифференциальное исчисление .

В рамках Ньютона законы, управляющие орбитами и траекториями, в принципе симметричны во времени .

Стандартные предположения астродинамики включают невмешательство внешних тел, незначительную массу одного из тел и незначительные другие силы (например, солнечный ветер, атмосферное сопротивление и т. Д.). Более точные расчеты можно провести и без этих упрощающих допущений, но они более сложны. Повышенная точность часто не оказывает такого существенного влияния на расчеты, чтобы иметь смысл.

Законы движения планет Кеплера могут быть выведены из законов Ньютона, когда предполагается, что вращающееся тело подчиняется только гравитационной силе центрального аттрактора. При наличии тяги двигателя или движущей силы законы Ньютона по-прежнему применяются, но законы Кеплера становятся недействительными. Когда тяга прекратится, результирующая орбита будет другой, но снова будет описываться законами Кеплера, изложенными выше. Три закона таковы:

1. Орбита которого находится каждой планеты представляет собой эллипс Солнце , в одном из фокусов .
2. Линия , соединяющая планету и Солнце, за равные промежутки времени охватывает равные площади.
3. Квадраты прямо обращения периодов планет пропорциональны кубам . большой полуоси орбит

Скорость убегания

Основная статья: Скорость убегания

Формула скорости убегания выводится следующим образом. Удельная энергия (энергия на единицу массы ) любого космического аппарата состоит из двух компонентов: удельной потенциальной энергии и удельной кинетической энергии . Удельная потенциальная энергия, связанная с планетой массы M, определяется выражением

$\epsilon _{p}=-{\frac {GM}{r}}\,$

где G — гравитационная постоянная , а r — расстояние между двумя телами;

а удельная кинетическая энергия объекта определяется выражением

$\epsilon _{k}={\frac {v^{2}}{2}}\,$

где v — его скорость;

и поэтому полная удельная орбитальная энергия равна

$\epsilon =\epsilon _{k}+\epsilon _{p}={\frac {v^{2}}{2}}-{\frac {GM}{r}}\,$

Поскольку энергия сохраняется , $\epsilon$ не может зависеть от расстояния, $r$, от центра центрального тела к рассматриваемому космическому аппарату, т.е. v должно меняться в зависимости от r, чтобы поддерживать постоянную удельную орбитальную энергию. Следовательно, объект может достигать бесконечности. $r$ только если эта величина неотрицательна, что означает

$v\geq {\sqrt {\frac {2GM}{r}}}.$

Скорость отрыва от поверхности Земли составляет около 11 км/с, но этого недостаточно, чтобы отправить тело на бесконечное расстояние из-за гравитационного притяжения Солнца. Чтобы покинуть Солнечную систему из места, находящегося на расстоянии от Солнца, равном расстоянию Солнце-Земля, но не близко к Земле, требуется скорость около 42 км/с, но будет «частичная заслуга» орбитальной скорости Земли. для космических аппаратов, запускаемых с Земли, если их дальнейшее ускорение (за счет двигательной установки) несет их в том же направлении, в котором движется Земля по своей орбите.

Формулы свободных орбит

Орбиты представляют собой конические сечения , поэтому формула расстояния тела для данного угла соответствует формуле этой кривой в полярных координатах , которая имеет вид:

$r={\frac {p}{1+e\cos \theta }}$

$\mu =G(m_{1}+m_{2})\,$

$p=h^{2}/\mu \,$

$\mu$ называется гравитационным параметром . $m_{1}$ и $m_{2}$ – массы объектов 1 и 2, а $h$ – удельный момент импульса объекта 2 относительно объекта 1. Параметр $\theta$ известна как истинная аномалия , $p$ это полурасширенная прямая кишка , в то время как $e$ - это эксцентриситет орбиты , который можно получить из различных форм шести независимых элементов орбиты .

Круговые орбиты

Основная статья: Круговая орбита

Все ограниченные орбиты, на которых доминирует гравитация центрального тела, имеют эллиптическую природу. Особым случаем является круговая орбита, представляющая собой эллипс с нулевым эксцентриситетом. Формулу скорости тела на круговой орбите на расстоянии r от центра тяжести M можно вывести следующим образом:

Центробежное ускорение соответствует ускорению свободного падения.

Так,

$${\frac {v^{2}}{r}}={\frac {GM}{r^{2}}}$$

Поэтому,

$\ v={\sqrt {{\frac {GM}{r}}\ }}$

где $G$ гравитационная постоянная , равная

6.6743 × 10 ⁻¹¹ м ³ /(кг·с ² )

Чтобы правильно использовать эту формулу, единицы измерения должны быть согласованными; например, $M$ должно быть в килограммах, а $r$ должно быть в метрах. Ответ будет в метрах в секунду.

Количество $GM$ часто называют стандартным гравитационным параметром , который имеет разное значение для каждой планеты или спутника Солнечной системы .

Зная круговую орбитальную скорость, можно легко найти скорость убегания , умножив на ${\sqrt {2}}$:

$\ v={\sqrt {2}}{\sqrt {{\frac {GM}{r}}\ }}={\sqrt {{\frac {2GM}{r}}\ }}.$

Чтобы избежать гравитации, кинетическая энергия должна как минимум соответствовать отрицательной потенциальной энергии. Поэтому,

$${\frac {1}{2}}mv^{2}={\frac {GMm}{r}}$$

$v={\sqrt {{\frac {2GM}{r}}\ }}.$

Эллиптические орбиты

Если $0<e<1$, то знаменатель уравнения свободных орбит меняется в зависимости от истинной аномалии $\theta$, но остается положительным и никогда не становится равным нулю. Следовательно, вектор относительного положения остается ограниченным, имея наименьшую величину в перицентре. $r_{p}$, который определяется:

$r_{p}={\frac {p}{1+e}}$

Максимальное значение $r$ достигается, когда $\theta =180^{\circ }$. Эту точку называют апоапсисом, а ее радиальную координату обозначают $r_{a}$, является

$r_{a}={\frac {p}{1-e}}$

Позволять $2a$ быть расстоянием, измеренным по линии апсиды от перицентра $P$ до апоапсиса $A$, как показано в уравнении ниже:

$2a=r_{p}+r_{a}$

Подставив приведенные выше уравнения, получим:

$a={\frac {p}{1-e^{2}}}$

а — большая полуось эллипса. Решение для $p$и подставив результат в приведенную выше формулу кривой конического сечения, мы получим:

$r={\frac {a(1-e^{2})}{1+e\cos \theta }}$

Орбитальный период

При стандартных предположениях орбитальный период ( $T\,\!$) тела, движущегося по эллиптической орбите, можно вычислить как:

$T=2\pi {\sqrt {a^{3} \over {\mu }}}$

где:

• $\mu \,$ — стандартный гравитационный параметр ,
• $a\,\!$ — длина большой полуоси .

Выводы:

• Орбитальный период равен таковому для круговой орбиты с радиусом орбиты, равным большой полуоси ( $a\,\!$),
• Для данной большой полуоси орбитальный период не зависит от эксцентриситета (См. также: Третий закон Кеплера ).

Скорость

При стандартных предположениях орбитальная скорость ( $v\,$) тела, движущегося по эллиптической орбите, можно вычислить из уравнения Vis-viva как:

$v={\sqrt {\mu \left({2 \over {r}}-{1 \over {a}}\right)}}$

где:

• $\mu \,$ — стандартный гравитационный параметр ,
• $r\,$ — расстояние между телами, вращающимися по орбите.
• $a\,\!$ — длина большой полуоси .

Уравнение скорости для гиперболической траектории имеет вид $v={\sqrt {\mu \left({2 \over {r}}+\left\vert {1 \over {a}}\right\vert \right)}}$.

Энергия

При стандартных предположениях удельная орбитальная энергия ( $\epsilon \,$) эллиптической орбиты отрицательно и уравнение сохранения орбитальной энергии ( уравнение Вис-вива ) для этой орбиты может иметь вид:

${v^{2} \over {2}}-{\mu \over {r}}=-{\mu \over {2a}}=\epsilon <0$

где:

• $v\,$ - скорость вращающегося тела,
• $r\,$ — расстояние вращающегося тела от центра масс центрального тела ,
• $a\,$ — большая полуось ,
• $\mu \,$ — стандартный гравитационный параметр .

Выводы:

• Для данной большой полуоси удельная орбитальная энергия не зависит от эксцентриситета.

Используя теорему вириала, находим:

• среднее по времени удельной потенциальной энергии равно $2\epsilon$
• среднее по времени $r^{-1}$ является $a^{-1}$
• среднее по времени удельной кинетической энергии равно $-\epsilon$

Параболические орбиты

Если эксцентриситет равен 1, то уравнение орбиты принимает вид:

$r={{h^{2}} \over {\mu }}{{1} \over {1+\cos \theta }}$

где:

• $r\,$ — радиальное расстояние вращающегося тела от центра масс центрального тела ,
• $h\,$ – удельный момент импульса тела вращающегося ,
• $\theta \,$ – истинная аномалия вращающегося тела,
• $\mu \,$ — стандартный гравитационный параметр .

Когда истинная аномалия θ приближается к 180°, знаменатель приближается к нулю, так что r стремится к бесконечности. Следовательно, энергия траектории, для которой e = 1, равна нулю и определяется выражением:

$\epsilon ={v^{2} \over 2}-{\mu \over {r}}=0$

где:

• $v\,$ - скорость вращающегося тела.

Другими словами, скорость в любой точке параболической траектории равна:

$v={\sqrt {2\mu \over {r}}}$

Гиперболические орбиты

Если $e>1$, формула орбиты,

$r={{h^{2}} \over {\mu }}{{1} \over {1+e\cos \theta }}$

описывает геометрию гиперболической орбиты. Система состоит из двух симметричных кривых. Вращающееся тело занимает одну из них; другой — его пустой математический образ. Очевидно, что знаменатель приведенного выше уравнения обращается в ноль, когда $\cos \theta =-1/e$. мы обозначаем это значение истинной аномалии

$\theta _{\infty }=\cos ^{-1}\left(-{\frac {1}{e}}\right)$

поскольку радиальное расстояние приближается к бесконечности по мере приближения истинной аномалии $\theta _{\infty }$, известную как истинная аномалия асимптоты . Обратите внимание, что $\theta _{\infty }$ лежит между 90° и 180°. Из тригонометрического тождества $\sin ^{2}\theta +\cos ^{2}\theta =1$ отсюда следует, что:

$\sin \theta _{\infty }={\frac {1}{e}}{\sqrt {e^{2}-1}}$

Энергия

При стандартных предположениях удельная орбитальная энергия ( $\epsilon \,$) гиперболической траектории больше нуля и уравнение сохранения орбитальной энергии для такой траектории принимает вид:

$\epsilon ={v^{2} \over 2}-{\mu \over {r}}={\mu \over {-2a}}$

где:

• $v\,$ - орбитальная скорость вращающегося тела,
• $r\,$ — радиальное расстояние вращающегося тела от центрального тела ,
• $a\,$ отрицательная полуось орбиты гиперболы большая — ,
• $\mu \,$ стандартный гравитационный параметр .

избыточная

Смотрите также: Характеристическая энергия

При стандартных предположениях тело, движущееся по гиперболической траектории, достигнет точки $r=$ бесконечность - орбитальная скорость , называемая гиперболической избыточной скоростью ( $v_{\infty }\,\!$), который можно вычислить как:

$v_{\infty }={\sqrt {\mu \over {-a}}}\,\!$

где:

• $\mu \,\!$ стандартный гравитационный параметр ,
• $a\,\!$ отрицательная полуось орбиты . гиперболы — большая

Гиперболическая избыточная скорость связана с удельной орбитальной энергией или характеристической энергией соотношением

$2\epsilon =C_{3}=v_{\infty }^{2}\,\!$

Расчет траекторий

Уравнение Кеплера

Один из подходов к расчету орбит (в основном используемый исторически) — использовать уравнение Кеплера :

$M=E-\epsilon \cdot \sin E$.

где M — средняя аномалия , E — эксцентрическая аномалия , и $\epsilon$ это эксцентриситет .

Используя формулу Кеплера, находим время пролета для достижения угла ( истинной аномалии ) $\theta$ от периапсиса разбивается на два этапа:

1. Вычислите эксцентрическую аномалию $E$ от настоящей аномалии $\theta$
2. Вычислить время полета $t$ из эксцентрической аномалии $E$

Найти эксцентрическую аномалию в данный момент времени ( обратная задача ) сложнее. Уравнение Кеплера трансцендентно по $E$, то есть ее невозможно решить за $E$ алгебраически . Уравнение Кеплера можно решить для $E$ аналитически путем инверсии.

Решение уравнения Кеплера, справедливое для всех действительных значений $\textstyle \epsilon$ является:

$$E={\begin{cases}\displaystyle \sum _{n=1}^{\infty }{\frac {M^{\frac {n}{3}}}{n!}}\lim _{\theta \to 0}\left({\frac {\mathrm {d} ^{\,n-1}}{\mathrm {d} \theta ^{\,n-1}}}\left[\left({\frac {\theta }{\sqrt[{3}]{\theta -\sin(\theta )}}}\right)^{n}\right]\right),&\epsilon =1\\\displaystyle \sum _{n=1}^{\infty }{\frac {M^{n}}{n!}}\lim _{\theta \to 0}\left({\frac {\mathrm {d} ^{\,n-1}}{\mathrm {d} \theta ^{\,n-1}}}\left[\left({\frac {\theta }{\theta -\epsilon \cdot \sin(\theta )}}\right)^{n}\right]\right),&\epsilon \neq 1\end{cases}}$$

Оценка этого дает:

$$E={\begin{cases}\displaystyle x+{\frac {1}{60}}x^{3}+{\frac {1}{1400}}x^{5}+{\frac {1}{25200}}x^{7}+{\frac {43}{17248000}}x^{9}+{\frac {1213}{7207200000}}x^{11}+{\frac {151439}{12713500800000}}x^{13}\cdots \ |\ x=(6M)^{\frac {1}{3}},&\epsilon =1\\\\\displaystyle {\frac {1}{1-\epsilon }}M-{\frac {\epsilon }{(1-\epsilon )^{4}}}{\frac {M^{3}}{3!}}+{\frac {(9\epsilon ^{2}+\epsilon )}{(1-\epsilon )^{7}}}{\frac {M^{5}}{5!}}-{\frac {(225\epsilon ^{3}+54\epsilon ^{2}+\epsilon )}{(1-\epsilon )^{10}}}{\frac {M^{7}}{7!}}+{\frac {(11025\epsilon ^{4}+4131\epsilon ^{3}+243\epsilon ^{2}+\epsilon )}{(1-\epsilon )^{13}}}{\frac {M^{9}}{9!}}\cdots ,&\epsilon \neq 1\end{cases}}$$

Альтернативно уравнение Кеплера можно решить численно. Сначала нужно угадать значение $E$ и определить время полета; затем отрегулируйте $E$ при необходимости приблизить вычисленное время пролета к желаемому значению до тех пор, пока не будет достигнута требуемая точность. Обычно метод Ньютона используется для достижения относительно быстрой сходимости.

Основная трудность этого подхода заключается в том, что сходимость крайних эллиптических орбит может занять непомерно много времени. Для околопараболических орбит эксцентриситет $\epsilon$ почти 1, и замена $e=1$ в формулу средней аномалии, $E-\sin E$, мы вычитаем два почти равных значения, и точность пострадает. Для почти круговых орбит вообще трудно найти периапсис (а действительно круговые орбиты вообще не имеют перицентра). Более того, уравнение было получено в предположении об эллиптической орбите, поэтому оно не справедливо для параболических или гиперболических орбит. Именно эти трудности привели к разработке формулировки универсальной переменной , описанной ниже.

Конические орбиты

Для простых процедур, таких как вычисление дельта-v для компланарных передаточных эллипсов, традиционные подходы являются достаточно эффективными. Другие, такие как времяпролетные, гораздо сложнее, особенно для околокруговых и гиперболических орбит.

Исправленная коническая аппроксимация

Основная статья: Исправленное коническое приближение

является Сама по себе переходная орбита Хомана плохим приближением для межпланетных траекторий, поскольку она не учитывает собственную гравитацию планет. Планетарная гравитация доминирует в поведении космического корабля вблизи планеты, и в большинстве случаев Хоманн сильно переоценивает дельту-v и дает крайне неточные рекомендации по времени горения. Относительно простой способ получить аппроксимацию дельта-v первого порядка основан на методе «патчированной конической аппроксимации». Необходимо выбрать одно доминирующее гравитирующее тело в каждой области пространства, через которую пройдет траектория, и моделировать эффекты только этого тела в этой области. Например, на траектории от Земли до Марса можно было бы начать с рассмотрения только гравитации Земли, пока траектория не достигнет расстояния, на котором гравитация Земли больше не будет доминировать над гравитацией Солнца. Космическому кораблю будет придана космическая скорость , чтобы отправить его в межпланетное пространство. Далее можно было бы учитывать только гравитацию Солнца, пока траектория не достигнет окрестностей Марса. На этом этапе подходит модель переходной орбиты. Наконец, на заключительном участке траектории, где гравитация Марса доминирует в поведении космического корабля, учитывается только гравитация Марса. Космический корабль приблизится к Марсу по гиперболической орбите, и последний ретроградный запуск замедлит космический корабль настолько, что его сможет захватить Марс. Фридрих Цандер был одним из первых, кто применил подход исправленных коник в целях астродинамики, предложив использовать гравитацию промежуточных тел для межпланетных путешествий в том, что сегодня известно как гравитационная помощь .

Размер «районов» (или сфер влияния ) варьируется в зависимости от радиуса. $r_{SOI}$:

$r_{SOI}=a_{p}\left({\frac {m_{p}}{m_{s}}}\right)^{2/5}$

где $a_{p}$ — большая полуось орбиты планеты относительно Солнца ; $m_{p}$ и $m_{s}$ – массы планеты и Солнца соответственно.

Этого упрощения достаточно для приблизительных оценок потребности в топливе и примерного времени полета, но оно, как правило, недостаточно точное, чтобы направить космический корабль к месту назначения. Для этого необходимы численные методы.

универсальной

Для устранения вычислительных недостатков традиционных подходов к решению задачи двух тел была разработана формулировка универсальной переменной . Он одинаково хорошо работает для кругового, эллиптического, параболического и гиперболического случаев, причем дифференциальные уравнения хорошо сходятся при интегрировании по любой орбите. Он также хорошо обобщается на задачи, включающие теорию возмущений.

Возмущения

Формулировка универсальной переменной хорошо работает с методом вариации параметров, за исключением того, что теперь вместо шести кеплеровских элементов орбиты мы используем другой набор элементов орбиты, а именно: начальное положение спутника и векторы скорости. $x_{0}$ и $v_{0}$ в данную эпоху $t=0$. В моделировании двух тел этих элементов достаточно, чтобы вычислить положение и скорость спутника в любой момент в будущем, используя формулировку универсальной переменной. И наоборот, в любой момент на орбите спутника мы можем измерить его положение и скорость, а затем использовать подход универсальных переменных, чтобы определить, какими были бы его начальное положение и скорость в данную эпоху. В идеальном движении двух тел эти орбитальные элементы были бы инвариантными (точно так же, как и кеплеровы элементы).

Однако возмущения заставляют элементы орбиты изменяться с течением времени. Следовательно, элемент позиции записывается как $x_{0}(t)$ и элемент скорости как $v_{0}(t)$, что указывает на то, что они меняются со временем. Методика расчета влияния возмущений сводится к нахождению точных или приближенных выражений для функций $x_{0}(t)$ и $v_{0}(t)$.

Ниже приведены некоторые эффекты, которые отличают реальные орбиты от простых моделей, основанных на сферической Земле. С большинством из них можно справиться в короткие сроки (возможно, менее нескольких тысяч витков) с помощью теории возмущений, поскольку они малы по сравнению с соответствующими эффектами двух тел.

• Экваториальные выпуклости вызывают прецессию узла и перигея.
• Тессеральные гармоники гравитационного поля вносят дополнительные возмущения
• Возмущения лунной и солнечной гравитации изменяют орбиты
• Атмосферное сопротивление уменьшает большую полуось, если не используется компенсационная тяга.

В очень длительных временных масштабах (возможно, миллионы орбит) даже небольшие возмущения могут доминировать, и поведение может стать хаотичным . С другой стороны, умные астродинамики могут организовать различные возмущения для выполнения задач по поддержанию орбиты, таких как поддержание местоположения , поддержание или корректировка наземного пути или фазирование перигея для покрытия выбранных целей на малой высоте.

Орбитальный маневр

Основная статья: Орбитальный маневр

В космическом полете орбитальный маневр — использование двигательных установок для изменения орбиты космического корабля . Для космических кораблей, находящихся далеко от Земли (например, находящихся на орбитах вокруг Солнца), орбитальный маневр называется маневром в дальнем космосе (DSM) .

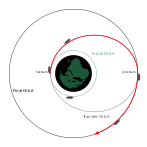
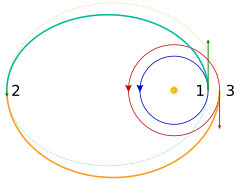
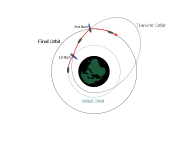
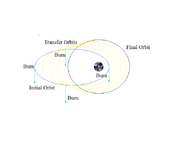
Орбитальный переход

Переходные орбиты обычно представляют собой эллиптические орбиты, которые позволяют космическому кораблю переходить с одной (обычно по существу круговой) орбиты на другую. Обычно они требуют ожога в начале, ожога в конце, а иногда и одного или нескольких ожогов в середине.

• требует Трансферная орбита Гомана минимального значения delta-v .
• Биэллиптический переход может потребовать меньше энергии, чем переход Гомана, если отношение орбит составляет 11,94 или больше. но это достигается за счет увеличения времени в пути из-за трансфера Хомана.
• Для более быстрой передачи можно использовать любую орбиту, которая пересекает как исходную, так и орбиту назначения, за счет более высокого значения delta-v.
• При использовании двигателей малой тяги (например, электрических силовых установок ), если начальная орбита суперсинхронна с конечной желаемой круговой орбитой, то оптимальная переходная орбита достигается за счет непрерывного движения в направлении скорости в апогее. Однако этот метод занимает гораздо больше времени из-за низкой тяги.

В случае перехода между некомпланарными орбитами тяга смены плоскости должна осуществляться в точке пересечения плоскостей орбит («узле»). Поскольку задача состоит в изменении направления вектора скорости на угол, равный углу между плоскостями, практически вся эта тяга должна осуществляться тогда, когда КА находится в узле вблизи апоапсиды, когда величина вектора скорости равна на самом низком уровне. Однако небольшая часть изменения наклонения орбиты может быть произведена в узле рядом с периапсидой, слегка наклонив тягу выведения на переходную орбиту в направлении желаемого изменения наклонения. Это работает, потому что косинус небольшого угла очень близок к единице, в результате чего небольшое изменение плоскости оказывается фактически «свободным», несмотря на высокую скорость космического корабля вблизи периапсы, поскольку эффект Оберта из-за увеличенной слегка наклоненной тяги превышает затраты. тяги по нормали орбиты.

с Переход Хомана низкой круговой орбиты на более высокую круговую орбиту.

Биэллиптический переход с низкой круговой стартовой орбиты (темно-синий) на более высокую круговую орбиту (красный)

Типичный двухимпульсный эллиптический переход между двумя круговыми орбитами

Общий переход с низкой круговой орбиты на более высокую круговую орбиту.

Оптимальная последовательность перевода спутника с суперсинхронной на геостационарную орбиту с использованием электродвижения

эффект

В гравитационном режиме космический корабль пролетает мимо планеты и уходит в другом направлении и с другой скоростью. Это полезно для ускорения или замедления космического корабля вместо того, чтобы нести больше топлива.

Этот маневр можно аппроксимировать упругим столкновением на больших расстояниях, хотя пролет не предполагает физического контакта. Согласно третьему закону Ньютона (равная и противоположная реакция), любой импульс, полученный космическим кораблем, должен быть потерян планетой, или наоборот. Однако, поскольку планета намного массивнее космического корабля, влияние на орбиту планеты незначительно.

Эффект Оберта может быть использован, особенно во время гравитационной операции. Этот эффект заключается в том, что использование двигательной установки лучше работает на высоких скоростях, и, следовательно, изменение курса лучше всего производить, находясь рядом с гравитационным телом; это может умножить эффективную delta-v .

Межпланетная транспортная сеть

Основная статья: Межпланетная транспортная сеть

См. Также: Низкая передача энергии.

Теперь можно использовать компьютеры для поиска маршрутов, используя нелинейности гравитации планет и спутников Солнечной системы. Например, можно построить орбиту от высокой околоземной орбиты до Марса, проходящую вблизи одной из троянских точек Земли . Эти крайне пертурбативные, даже хаотичные орбитальные траектории , называемые под общим названием « Межпланетная транспортная сеть» , в принципе не нуждаются в топливе, кроме того, которое необходимо для достижения точки Лагранжа (на практике соблюдение траектории требует некоторых корректировок курса). Самая большая проблема с ними в том, что они могут быть чрезвычайно медленными и занимать многие годы. Кроме того, окна запуска могут находиться очень далеко друг от друга.

Однако они были задействованы в таких проектах, как Genesis . Земля-Солнце Этот космический корабль посетил точку L ₁ и вернулся, используя очень мало топлива.

См. также

• Небесная механика
• Теория хаоса
• Кеплер орбита
• Точка Лагранжа
• Машиностроение
• Проблема N-тела
• Предел Роша
• Движение космического корабля
• Универсальная формулировка переменной

Ссылки

• Кертис, Ховард Д. (2009). Орбитальная механика для студентов-инженеров, 2е . Нью-Йорк: Эльзевир. ISBN  978-0-12-374778-5 .
• Бейт, Роджер Р.; Мюллер, Дональд Д.; Уайт, Джерри Э. (1971). Основы астродинамики . Нью-Йорк: Dover Publications. ISBN  0-486-60061-0 .

• Селлерс, Джерри Дж.; Астор, Уильям Дж.; Гиффен, Роберт Б.; Ларсон, Уайли Дж. (2004). Киркпатрик, Дуглас Х. (ред.). Понимание космоса: введение в космонавтику (2-е изд.). МакГроу Хилл. п. 228. ИСБН  0-07-242468-0 .

• «Букварь по космосу в Авиационном университете, Глава 8 — Орбитальная механика» (PDF) . ВВС США. Архивировано из оригинала (PDF) 14 февраля 2013 г. Проверено 13 октября 2007 г.

Дальнейшее чтение

Многие варианты, процедуры и вспомогательная теория описаны в стандартных работах, таких как:

• Бейт, РР; Мюллер, Д.Д.; Уайт, Дж. Э. (1971). Основы астродинамики . Dover Publications, Нью-Йорк. ISBN  978-0-486-60061-1 .
• Валладо, Д.А. (2001). Основы астродинамики и приложений (2-е изд.). Спрингер. ISBN  978-0-7923-6903-5 .
• Баттин, Р.Х. (1999). Введение в математику и методы астродинамики . Американский институт аэронавтики и технологий, Вашингтон, округ Колумбия, ISBN  978-1-56347-342-5 .
• Чоботов В.А., изд. (2002). Орбитальная механика (3-е изд.). Американский институт аэронавтики и технологий, Вашингтон, округ Колумбия, ISBN  978-1-56347-537-5 .
• Херрик, С. (1971). Астродинамика: Определение орбиты, Космическая навигация, Небесная механика, Том 1 . Ван Ностранд Рейнхольд, Лондон. ISBN  978-0-442-03370-5 .
• Херрик, С. (1972). Астродинамика: коррекция орбиты, теория возмущений, интегрирование, том 2 . Ван Ностранд Рейнхольд, Лондон. ISBN  978-0-442-03371-2 .
• Каплан, Миннесота (1976). Динамика и управление современных космических аппаратов . Уайли, Нью-Йорк. ISBN  978-0-471-45703-9 .
• Том Логсдон (1997). Орбитальная механика . Уайли-Интерсайенс, Нью-Йорк. ISBN  978-0-471-14636-0 .
• Джон Э. Пруссинг и Брюс А. Конвей (1993). Орбитальная механика . Издательство Оксфордского университета, Нью-Йорк. ISBN  978-0-19-507834-3 .
• МДж Сиди (2000). Динамика и управление космическим кораблем . Издательство Кембриджского университета, Нью-Йорк. ISBN  978-0-521-78780-2 .
• МЫ Визель (1996). Динамика космического полета (2-е изд.). МакГроу-Хилл, Нью-Йорк. ISBN  978-0-07-070110-6 .
• Дж. П. Винти (1998). Орбитальная и небесная механика . Американский институт аэронавтики и технологий, Рестон, Вирджиния. ISBN  978-1-56347-256-5 .
• П. Гурфил (2006). Современная астродинамика . Баттерворт-Хайнеманн. ISBN  978-0-12-373562-1 .

Внешние ссылки

• ОРБИТАЛЬНАЯ МЕХАНИКА (Ракетная и космическая техника)
• Набор инструментов Java для астродинамики
• График знаний о космическом движении и событиях на основе астродинамики