Эксцентриситет орбиты

В астродинамике эксцентриситет орбиты — астрономического объекта безразмерный параметр , определяющий, насколько его орбита вокруг другого тела отклоняется от идеального круга . Значение 0 соответствует круговой орбите , значения от 0 до 1 образуют эллиптическую орбиту , 1 — параболическую орбиту ухода (или орбиту захвата), а значение больше 1 — гиперболу . Этот термин получил свое название от параметров конических сечений , поскольку каждая орбита Кеплера является коническим сечением. Обычно он используется для изолированной задачи двух тел , но существуют расширения для объектов, следующих по розеточной орбите через Галактику.

Определение

В задаче двух тел с силой обратных квадратов каждая орбита является орбитой Кеплера . Эксцентриситет , этой орбиты Кеплера — неотрицательное число определяющее ее форму.

Эксцентриситет может принимать следующие значения:

Эксцентриситет e определяется выражением ^[1]

$e={\sqrt {1+{\frac {2EL^{2}}{m_{\text{red}}\,\alpha ^{2}}}}}$

где $E$ — полная орбитальная энергия , $L$ — угловой момент , $m red$ — приведенная масса , и $\alpha$ коэффициент центральной силы закона обратных квадратов , например, в теории гравитации или электростатике в классической физике : $F={\frac {\alpha }{r^{2}}}$ ( $\alpha$ отрицательна для силы притяжения, положительна для отталкивающей; связанное с проблемой Кеплера )

или в случае гравитационной силы: ^[2]^: 24 $e={\sqrt {1+{\frac {2\varepsilon h^{2}}{\mu ^{2}}}}}$

где $ε$ — удельная орбитальная энергия (полная энергия, деленная на приведенную массу), $μ —$ стандартный гравитационный параметр, основанный на полной массе, а $h —$ удельный относительный угловой момент ( угловой момент, деленный на приведенную массу). ^[2]^: 12–17

Для значений e от 0 до 1 форма орбиты представляет собой все более вытянутый (или более плоский) эллипс; для значений e от 1 до бесконечности орбита представляет собой ветвь гиперболы, совершающую полный оборот на 2 arccsc ( e ) , уменьшающуюся от 180 до 0 градусов. Здесь полный поворот аналогичен числу поворотов , но для открытых кривых (угол, охватываемый вектором скорости). Предельный случай между эллипсом и гиперболой, когда e равно 1, является параболой.

Радиальные траектории классифицируются как эллиптические, параболические или гиперболические в зависимости от энергии орбиты, а не эксцентриситета. Радиальные орбиты имеют нулевой угловой момент и, следовательно, эксцентриситет равен единице. При сохранении постоянной энергии и уменьшении углового момента каждая эллиптическая, параболическая и гиперболическая орбиты стремятся к соответствующему типу радиальной траектории, в то время как e стремится к 1 (или в параболическом случае остается 1).

Для силы отталкивания применима только гиперболическая траектория, включая радиальный вариант.

Для эллиптических орбит простое доказательство показывает, что $\arcsin(e)$ дает угол проекции идеального круга на эллипс с эксцентриситетом e . Например, чтобы просмотреть эксцентриситет планеты Меркурий ( e = 0,2056), нужно просто вычислить обратный синус , чтобы найти угол проекции 11,86 градуса. Тогда, наклонив любой круглый объект на этот угол, видимый эллипс этого объекта, проецируемый на глаз зрителя, будет иметь такой же эксцентриситет.

Этимология

Слово «эксцентричность» происходит от средневекового латинского eccentricus , происходящего от греческого ἔκκεντρος ekkentros «вне центра», от ἐκ- ek- «вне» + κέντρον kentron «центр». Слово «эксцентрик» впервые появилось на английском языке в 1551 году с определением «...круг, в котором земля, солнце и т. д. отклоняются от своего центра». ^{[ нужна ссылка ]} В 1556 году, пять лет спустя, сложилась прилагательная форма этого слова.

Расчет

Эксцентриситет орбиты можно рассчитать по векторам состояния орбиты как величину эксцентриситета вектора : $e=\left|\mathbf {e} \right|$ где:

$e$ — вектор эксцентриситета ( «вектор Гамильтона» ). ^[2]^{: 25, 62–63}

Для эллиптических орбит его также можно рассчитать по перицентру и апоцентру , поскольку $r_{\text{p}}=a\,(1-e)$ и $r_{\text{a}}=a\,(1+e)\,,$ где $а$ — длина большой полуоси . ${\begin{aligned}e&={\frac {r_{\text{a}}-r_{\text{p}}}{r_{\text{a}}+r_{\text{p}}}}\\\,\\&={\frac {r_{\text{a}}/r_{\text{p}}-1}{r_{\text{a}}/r_{\text{p}}+1}}\\\,\\&=1-{\frac {2}{\;{\frac {r_{\text{a}}}{r_{\text{p}}}}+1\;}}\end{aligned}}$ где:

$r$ _a — радиус апоапсиса (также «апофокус», «афелий», «апогей»), т. е. наибольшее расстояние орбиты до центра масс системы, который является фокусом эллипса.
$r$ _p — радиус в перицентре (или «перифокусе» и т. д.), ближайшем расстоянии.

Большая полуось a также представляет собой усредненное по пути расстояние до центра масс: ^[2]^: 24–25 а усредненное по времени расстояние равно a(1 + ee/2). [1]

Эксцентриситет эллиптической орбиты можно использовать для получения отношения радиуса апоцентра к радиусу перицентра : ${\frac {r_{\text{a}}}{r_{\text{p}}}}={\frac {\,a\,(1+e)\,}{\,a\,(1-e)\,}}={\frac {1+e}{1-e}}$

Для Земли эксцентриситет орбиты $e \approx 0,016 71$ , апоцентр — это афелий, а периапсис — перигелий относительно Солнца.

Для годовой орбиты Земли отношение самого длинного радиуса ( $ra$ ₎ / самого короткого радиуса ( $r$ _p ) равно ${\frac {\,r_{\text{a}}\,}{r_{\text{p}}}}={\frac {\,1+e\,}{1-e}}{\text{ ≈ 1.03399 .}}$

Примеры

Эксцентриситеты тел Солнечной системы
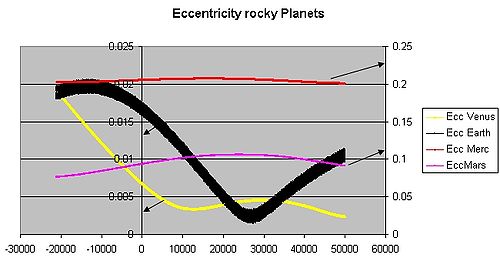
Объект	Эксцентриситет
Тритон	0.000 02
Венера	0.006 8
Нептун	0.008 6
Земля	0.016 7
Титан	0.028 8
Уран	0.047 2
Юпитер	0.048 4
Сатурн	0.054 1
Луна (Луна)	0.054 9
Церера	0.075 8
Веста	0.088 7
Марс	0.093 4
10 Гигея	0.114 6
хотелось бы	0.155 9
Грязный	0.188 7
Меркурий	0.205 6
2 Палласа	0.231 3
Плутон	0.248 8
3 июня	0.255 5
324 Бамберга	0.340 0
Эрис	0.440 7
Нереида	0.750 7
Седна	0.854 9
Комета Галлея	0.967 1
Комета Хейла-Боппа	0.995 1
Комета Икея-Секи	0.999 9
Комета МакНота	1.000 2 ^[а]
С/1980 Е1	1.057
Прежде всего	1.20 ^[б]
2I/Borisov	3.5 ^[с]

В таблице приведены значения для всех планет и карликовых планет, а также выбранных астероидов, комет и спутников. Меркурий имеет самый большой эксцентриситет орбиты среди всех планет Солнечной системы ( e = 0,2056 ), за ним следует Марс с 0,093 4 . Такого эксцентриситета достаточно, чтобы Меркурий получал вдвое больше солнечного излучения в перигелии, чем в афелии. До понижения статуса планеты в 2006 году Плутон считался планетой с самой эксцентричной орбитой ( e = 0,248 ). Другие транснептуновые объекты имеют значительный эксцентриситет, особенно карликовая планета Эрида (0,44). Еще дальше Седна имеет чрезвычайно высокий эксцентриситет 0,855 из-за ее предполагаемого афелия 937 а.е. и перигелия около 76 а.е., возможно, под влиянием неизвестного объекта(ов) .

Эксцентриситет орбиты Земли время составляет около 0,0167 ; в настоящее его орбита почти круговая. Нептун и Венера меньший эксцентриситет — и 0,0086 0,0068 соответственно имеют еще , причем последний является наименьшим эксцентриситетом орбиты среди всех планет Солнечной системы. За сотни тысяч лет эксцентриситет орбиты Земли изменяется от почти до 0,0034 почти 0,058 в результате гравитационного притяжения между планетами. ^[3]

Луны Значение составляет 0,054 9 , это самая эксцентричная из больших лун Солнечной системы. Четыре галилеевых спутника ( Ио , Европа , Ганимед и Каллисто ) имеют эксцентриситет менее 0,01. Нептуна Самый большой спутник Тритон имеет эксцентриситет 1,6 × 10. ⁻⁵ ( 0.000 016 ), ^[4] наименьший эксцентриситет среди всех известных спутников Солнечной системы; ^{[ нужна ссылка ]} его орбита настолько близка к идеальному кругу, насколько это возможно в настоящее время. ^{[ когда? ]} измерено. Спутники меньшего размера, особенно спутники неправильной формы , могут иметь значительный эксцентриситет, например, третий по величине спутник Нептуна, Нереида , равный 0,75 .

Солнечной системы Большинство астероидов имеют эксцентриситет орбит от 0 до 0,35 со средним значением 0,17. ^[5] Их сравнительно высокий эксцентриситет, вероятно, обусловлен влиянием Юпитера и прошлыми столкновениями.

Кометы имеют очень разные значения эксцентриситета. периодических комет обычно составляет от 0,2 до 0,7. Эксцентриситет ^[6] но некоторые из них имеют сильно эксцентричные эллиптические орбиты с эксцентриситетом чуть ниже 1; например, комета Галлея имеет значение 0,967. Непериодические кометы движутся по почти параболическим орбитам и, таким образом, имеют эксцентриситет еще ближе к 1. Примеры включают комету Хейла-Боппа со значением 0,995 1 , ^[7] Комета Икея-Секи со значением 0,999 9 и комета МакНота (C/2006 P1) со значением 1,000 019 . ^[8] Поскольку значения первых двух меньше 1, их орбита эллиптическая, и они вернутся. ^[7] У Макнота гиперболическая орбита , но она находится под влиянием планет. ^[8] все еще связан с Солнцем с орбитальным периодом около 10 ⁵ годы. ^[9] Комета C/1980 E1 имеет самый большой эксцентриситет среди всех известных гиперболических комет солнечного происхождения с эксцентриситетом 1,057. ^[10] и в конечном итоге покинет Солнечную систему.

Оумуамуа — первый межзвездный объект , проходящий через Солнечную систему. Эксцентриситет его орбиты 1,20 указывает на то, что Оумуамуа никогда не был гравитационно связан с Солнцем. Он был обнаружен на расстоянии 0,2 а.е. ( 30 000 000 км; 19 000 000 миль) от Земли и имеет диаметр примерно 200 метров. Его межзвездная скорость (скорость на бесконечности) составляет 26,33 км/с ( 58 900 миль в час).

Среднее среднее

Средний эксцентриситет объекта — это средний эксцентриситет в результате возмущений за данный период времени. Нептун в настоящее время имеет мгновенный (текущая эпоха ) эксцентриситет 0,011 3 , ^[11] 1800 по 2050 год средний эксцентриситет составлял 0,00859 но с . ^[12]

Климатический эффект

Орбитальная механика требует, чтобы продолжительность сезонов была пропорциональна площади земной орбиты, проходящей между солнцестояниями и равноденствиями , поэтому, когда орбитальный эксцентриситет экстремальный, сезоны, которые происходят на дальней стороне орбиты ( афелии ), могут быть существенно длиннее. по продолжительности. Осень и зима в северном полушарии происходят при наибольшем сближении ( перигелии ), когда Земля движется с максимальной скоростью, тогда как в южном полушарии происходит обратное. В результате в северном полушарии осень и зима немного короче весны и лета, но в глобальном плане это уравновешивается тем, что они длиннее ниже экватора. В 2006 году лето в северном полушарии было на 4,66 дня длиннее зимы, а весна на 2,9 дня длиннее осени из-за эксцентриситета орбиты. ^[13]^[14]

Апсидальная прецессия также медленно меняет место на орбите Земли, где происходят солнцестояния и равноденствия. Это медленное изменение орбиты Земли, а не оси вращения, которое называется осевой прецессией . Климатические последствия этого изменения являются частью циклов Миланковича . В течение следующих 10 000 лет зима в северном полушарии постепенно станет длиннее, а лето — короче. Любой эффект охлаждения в одном полушарии уравновешивается потеплением в другом, а любому общему изменению будет противодействовать тот факт, что эксцентриситет орбиты Земли уменьшится почти вдвое. ^[15] Это уменьшит средний радиус орбиты и повысит температуру в обоих полушариях ближе к пику середины межледниковья.

Экзопланеты

Из многих обнаруженных экзопланет большинство имеют более высокий эксцентриситет орбиты, чем планеты Солнечной системы. Обнаруженные экзопланеты с низким эксцентриситетом орбиты (почти круговые орбиты) расположены очень близко к своей звезде и приливно-приливно привязаны к звезде. Все восемь планет Солнечной системы имеют околокруговые орбиты. Обнаруженные экзопланеты показывают, что Солнечная система с ее необычайно низким эксцентриситетом является редкой и уникальной. ^[16] Одна теория объясняет этот низкий эксцентриситет большим количеством планет в Солнечной системе; другой предполагает, что он возник из-за уникальных поясов астероидов. несколько других многопланетных систем Было обнаружено , но ни одна из них не похожа на Солнечную систему. Солнечная система имеет уникальные планетезимальные системы, благодаря которым планеты имеют почти круговые орбиты. Солнечные планетезимальные системы включают пояс астероидов , семейство Хильда , пояс Койпера , облако Хиллса и облако Оорта . Обнаруженные экзопланетные системы либо не имеют планетезимальных систем, либо имеют очень большую систему. Низкий эксцентриситет необходим для обитаемости, особенно для продвинутой жизни. ^[17] Планетные системы с высокой множественностью с гораздо большей вероятностью будут иметь обитаемые экзопланеты. ^[18]^[19] Гипотеза «большого поворота» Солнечной системы также помогает понять ее почти круговые орбиты и другие уникальные особенности. ^[20]^[21]^[22]^[23]^[24]^[25]^[26]^[27]

См. также

Уравнение времени

Сноски

^ Хотя его орбита гиперболическая, однако она все еще связана с Солнцем из-за влияния планет.
^ ` Оумуамуа никогда не был связан с Солнцем, поэтому его орбита гиперболическая: $e$ ≈ 1,20 > 1
^ C/2019 Q4 (Борисов) никогда не был связан с Солнцем, поэтому его орбита гиперболическая: $e$ ≈ 3,5 > 1.

Ссылки

^ Авраам, Ральф (2008). Основы механики . Джеррольд Э. Марсден (2-е изд.). Провиденс, Род-Айленд: Паб AMS Chelsea/Американское математическое общество. ISBN 978-0-8218-4438-0 . OCLC 191847156 .
^ Jump up to: Перейти обратно: ^а ^б ^с ^д Бейт, Роджер Р.; Мюллер, Дональд Д.; Уайт, Джерри Э.; Сэйлор, Уильям В. (2020). Основы астродинамики . Курьер Дувр . ISBN 978-0-486-49704-4 . Проверено 4 марта 2022 г.
^ А. Бергер и М. Ф. Лутре (1991). «График эксцентриситета орбиты Земли» . Государственный музей Иллинойса (значения инсоляции для климата за последние 10 миллионов лет). Архивировано из оригинала 6 января 2018 года.
^ Дэвид Р. Уильямс (22 января 2008 г.). «Информационный бюллетень о спутнике Нептуна» . НАСА.
↑ Астероиды . Архивировано 4 марта 2007 г. в Wayback Machine.
^ Льюис, Джон (2 декабря 2012 г.). Физика и химия Солнечной системы . Академическая пресса. ISBN 9780323145848 .
^ Jump up to: Перейти обратно: ^а ^б «Обозреватель базы данных малых тел JPL: C/1995 O1 (Hale-Bopp)» (последние наблюдения 22 октября 2007 г.) . Проверено 5 декабря 2008 г.
^ Jump up to: Перейти обратно: ^а ^б «Обозреватель базы данных малых тел JPL: C/2006 P1 (McNaught)» (последние наблюдения 11 июля 2007 г.) . Проверено 17 декабря 2009 г.
^ «Комета C/2006 P1 (Макнота) – факты и цифры» . Пертская обсерватория в Австралии. 22 января 2007 г. Архивировано из оригинала 18 февраля 2011 г.
^ «Обозреватель базы данных малых тел JPL: C/1980 E1 (Боуэлл)» (последние наблюдения 2 декабря 1986 г.) . Проверено 22 марта 2010 г.
^ Уильямс, Дэвид Р. (29 ноября 2007 г.). «Информационный бюллетень о Нептуне» . НАСА.
^ «Кеплеровы элементы для 1800–2050 годов нашей эры» JPL «Динамика солнечной системы » . Проверено 17 декабря 2009 г.
↑ Данные Военно-морской обсерватории США, архивированные 13 октября 2007 г. на Wayback Machine.
^ Бергер А.; Лутре МФ; Мелис Дж.Л. (2006). «Экваториальная инсоляция: от гармоник прецессии до частот эксцентриситета» (PDF) . Клим. Прошлое Обсудить . 2 (4): 519–533. doi : 10.5194/cpd-2-519-2006 .
^ «Долгосрочный климат» . ircamera.as.arizona.edu . Архивировано из оригинала 2 июня 2015 года . Проверено 1 сентября 2016 г.
^ «ЭКЦЦЕНТРИЧНОСТЬ» . exoplanets.org .
^ Уорд, Питер; Браунли, Дональд (2000). Редкая Земля: почему сложная жизнь во Вселенной встречается редко . Спрингер. стр. 122–123. ISBN 0-387-98701-0 .
^ Лимбах, Массачусетс; Тернер, Э.Л. (2015). «Эксцентриситет орбиты экзопланеты: соотношение множественности и Солнечная система» . Proc Natl Acad Sci США . 112 (1): 20–4. arXiv : 1404.2552 . Бибкод : 2015PNAS..112...20L . дои : 10.1073/pnas.1406545111 . ПМК 4291657 . ПМИД 25512527 .
^ Юдин, Эндрю Н.; Рике, Джордж Х. (15 декабря 2015 г.). «Планетезимали в дисках обломков». arXiv : 1512.04996 . {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь )
^ Зубрицкий, Елизавета. «Юношеские путешествия Юпитера изменили определение Солнечной системы» . НАСА . Архивировано из оригинала 9 июня 2011 года . Проверено 4 ноября 2015 г.
^ Сандерс, Рэй (23 августа 2011 г.). «Как Юпитер сформировал нашу Солнечную систему?» . Вселенная сегодня . Проверено 4 ноября 2015 г.
^ Чой, Чарльз К. (23 марта 2015 г.). «Сокрушительная миграция Юпитера может объяснить нашу странную Солнечную систему» . Space.com . Проверено 4 ноября 2015 г.
^ Дэвидссон, доктор Бьорн-младший (9 марта 2014 г.). «Тайны пояса астероидов» . История Солнечной системы . Проверено 7 ноября 2015 г.
^ Раймонд, Шон (2 августа 2013 г.). «Большой Такс» . ПланетаПланета . Проверено 7 ноября 2015 г.
^ О'Брайен, Дэвид П.; Уолш, Кевин Дж.; Морбиделли, Алессандро; Раймонд, Шон Н.; Манделл, Ави М. (2014). «Доставка воды и гигантские воздействия в сценарии «Grand Tack»». Икар . 239 : 74–84. arXiv : 1407.3290 . Бибкод : 2014Icar..239...74O . дои : 10.1016/j.icarus.2014.05.009 . S2CID 51737711 .
^ Леб, Авраам; Батиста, Рафаэль; Слоан, Дэвид (август 2016 г.). «Относительная вероятность жизни как функция космического времени». Журнал космологии и физики астрочастиц . 2016 (8): 040. arXiv : 1606.08448 . Бибкод : 2016JCAP...08..040L . дои : 10.1088/1475-7516/2016/08/040 . S2CID 118489638 .
^ «Является ли земная жизнь преждевременной с космической точки зрения?» . Гарвард-Смитсоновский центр астрофизики. 1 августа 2016 г.

Дальнейшее чтение

Пруссинг, Джон Э.; Конвей, Брюс А. (1993). Орбитальная механика . Нью-Йорк: Издательство Оксфордского университета. ISBN 0-19-507834-9 .

Внешние ссылки

Мир физики: Эксцентриситет
Страница NOAA, посвященная данным о воздействии на климат, включает (расчетные) данные Бергера (1978), Бергера и Лутре (1991). ^{[ постоянная мертвая ссылка ]}. Ласкар и др. (2004) об изменениях орбиты Земли. Включает эксцентриситет за последние 50 миллионов лет и в ближайшие 20 миллионов лет.
Орбитальное моделирование, проведенное Варади, Гилом и Раннегаром (2003), предоставляет ряд данных об эксцентриситете и наклонении орбиты Земли.
Моделирование второго закона Кеплера

[3] Хотя его орбита гиперболическая, однако она все еще связана с Солнцем из-за влияния планет.

[4] ^ ` Оумуамуа никогда не был связан с Солнцем, поэтому его орбита гиперболическая: $e$ ≈ 1,20 > 1

[5] C/2019 Q4 (Борисов) никогда не был связан с Солнцем, поэтому его орбита гиперболическая: $e$ ≈ 3,5 > 1.

[1] Авраам, Ральф (2008). Основы механики . Джеррольд Э. Марсден (2-е изд.). Провиденс, Род-Айленд: Паб AMS Chelsea/Американское математическое общество. ISBN 978-0-8218-4438-0 . OCLC 191847156 .

[BateEtAl-2] Jump up to: Перейти обратно: ^а ^б ^с ^д Бейт, Роджер Р.; Мюллер, Дональд Д.; Уайт, Джерри Э.; Сэйлор, Уильям В. (2020). Основы астродинамики . Курьер Дувр . ISBN 978-0-486-49704-4 . Проверено 4 марта 2022 г.

[Berger1991-6] А. Бергер и М. Ф. Лутре (1991). «График эксцентриситета орбиты Земли» . Государственный музей Иллинойса (значения инсоляции для климата за последние 10 миллионов лет). Архивировано из оригинала 6 января 2018 года.

[Triton-7] Дэвид Р. Уильямс (22 января 2008 г.). «Информационный бюллетень о спутнике Нептуна» . НАСА.

[8] Астероиды . Архивировано 4 марта 2007 г. в Wayback Machine.

[Comets-9] Льюис, Джон (2 декабря 2012 г.). Физика и химия Солнечной системы . Академическая пресса. ISBN 9780323145848 .

[Hale-Bopp-jpl-10] Jump up to: Перейти обратно: ^а ^б «Обозреватель базы данных малых тел JPL: C/1995 O1 (Hale-Bopp)» (последние наблюдения 22 октября 2007 г.) . Проверено 5 декабря 2008 г.

[McNaught-jpl-11] Jump up to: Перейти обратно: ^а ^б «Обозреватель базы данных малых тел JPL: C/2006 P1 (McNaught)» (последние наблюдения 11 июля 2007 г.) . Проверено 17 декабря 2009 г.

[Perth-12] «Комета C/2006 P1 (Макнота) – факты и цифры» . Пертская обсерватория в Австралии. 22 января 2007 г. Архивировано из оригинала 18 февраля 2011 г.

[C/1980E1-jpl-13] «Обозреватель базы данных малых тел JPL: C/1980 E1 (Боуэлл)» (последние наблюдения 2 декабря 1986 г.) . Проверено 22 марта 2010 г.

[nssdc-Neptune-14] Уильямс, Дэвид Р. (29 ноября 2007 г.). «Информационный бюллетень о Нептуне» . НАСА.

[ssd-mean-15] «Кеплеровы элементы для 1800–2050 годов нашей эры» JPL «Динамика солнечной системы » . Проверено 17 декабря 2009 г.

[16] Данные Военно-морской обсерватории США, архивированные 13 октября 2007 г. на Wayback Machine.

[17] Бергер А.; Лутре МФ; Мелис Дж.Л. (2006). «Экваториальная инсоляция: от гармоник прецессии до частот эксцентриситета» (PDF) . Клим. Прошлое Обсудить . 2 (4): 519–533. doi : 10.5194/cpd-2-519-2006 .

[18] «Долгосрочный климат» . ircamera.as.arizona.edu . Архивировано из оригинала 2 июня 2015 года . Проверено 1 сентября 2016 г.

[19] «ЭКЦЦЕНТРИЧНОСТЬ» . exoplanets.org .

[20] Уорд, Питер; Браунли, Дональд (2000). Редкая Земля: почему сложная жизнь во Вселенной встречается редко . Спрингер. стр. 122–123. ISBN 0-387-98701-0 .

[21] Лимбах, Массачусетс; Тернер, Э.Л. (2015). «Эксцентриситет орбиты экзопланеты: соотношение множественности и Солнечная система» . Proc Natl Acad Sci США . 112 (1): 20–4. arXiv : 1404.2552 . Бибкод : 2015PNAS..112...20L . дои : 10.1073/pnas.1406545111 . ПМК 4291657 . ПМИД 25512527 .

[22] Юдин, Эндрю Н.; Рике, Джордж Х. (15 декабря 2015 г.). «Планетезимали в дисках обломков». arXiv : 1512.04996 . {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь )

[Zubritsky_2011-23] Зубрицкий, Елизавета. «Юношеские путешествия Юпитера изменили определение Солнечной системы» . НАСА . Архивировано из оригинала 9 июня 2011 года . Проверено 4 ноября 2015 г.

[Sanders_2011-24] Сандерс, Рэй (23 августа 2011 г.). «Как Юпитер сформировал нашу Солнечную систему?» . Вселенная сегодня . Проверено 4 ноября 2015 г.

[Choi_2015-25] Чой, Чарльз К. (23 марта 2015 г.). «Сокрушительная миграция Юпитера может объяснить нашу странную Солнечную систему» . Space.com . Проверено 4 ноября 2015 г.

[Davidsson_2014-26] Дэвидссон, доктор Бьорн-младший (9 марта 2014 г.). «Тайны пояса астероидов» . История Солнечной системы . Проверено 7 ноября 2015 г.

[Raymond_2013-27] Раймонд, Шон (2 августа 2013 г.). «Большой Такс» . ПланетаПланета . Проверено 7 ноября 2015 г.

[O'Brien_2014-28] О'Брайен, Дэвид П.; Уолш, Кевин Дж.; Морбиделли, Алессандро; Раймонд, Шон Н.; Манделл, Ави М. (2014). «Доставка воды и гигантские воздействия в сценарии «Grand Tack»». Икар . 239 : 74–84. arXiv : 1407.3290 . Бибкод : 2014Icar..239...74O . дои : 10.1016/j.icarus.2014.05.009 . S2CID 51737711 .

[29] Леб, Авраам; Батиста, Рафаэль; Слоан, Дэвид (август 2016 г.). «Относительная вероятность жизни как функция космического времени». Журнал космологии и физики астрочастиц . 2016 (8): 040. arXiv : 1606.08448 . Бибкод : 2016JCAP...08..040L . дои : 10.1088/1475-7516/2016/08/040 . S2CID 118489638 .

[30] «Является ли земная жизнь преждевременной с космической точки зрения?» . Гарвард-Смитсоновский центр астрофизики. 1 августа 2016 г.

[1]

[2]

[а]

[б]

[с]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]