Гиперболическая траектория

Синий путь на этом изображении является примером гиперболической траектории.

В астродинамике или небесной механике гиперболическая траектория или гиперболическая орбита — это траектория любого объекта вокруг центрального тела со скоростью, более чем достаточной для того, чтобы избежать гравитационного притяжения центрального объекта. Название происходит от того, что согласно теории Ньютона такая орбита имеет форму гиперболы . В более технических терминах это можно выразить условием, что эксцентриситет орбиты больше единицы.

При упрощенных предположениях тело, движущееся по этой траектории, будет стремиться к бесконечности, достигая конечной избыточной скорости относительно центрального тела. Подобно параболическим траекториям , все гиперболические траектории также являются траекториями ухода . Удельная энергия орбиты гиперболической траектории положительна.

Облеты планет, используемые для гравитационных рогаток планеты , можно описать в сфере влияния с помощью гиперболических траекторий.

Параметры, описывающие гиперболическую траекторию

Как и эллиптическая орбита, гиперболическая траектория для данной системы может быть определена (без учета ориентации) по ее большой полуоси и эксцентриситету. Однако при гиперболической орбите другие параметры могут оказаться более полезными для понимания движения тела. В следующей таблице перечислены основные параметры, описывающие путь тела по гиперболической траектории вокруг другого при стандартных предположениях, и формула, связывающая их.

Уравнения гиперболических траекторий ^[1]
Элемент	Символ	Формула	с использованием $v_{\infty }$ (или $a$ ), и $b$
Стандартный гравитационный параметр	$\mu \,$	${\frac {v^{2}}{(2/r-1/a)}}$	$bv_{\infty }^{2}\cot \theta _{\infty }$
Эксцентриситет (>1)	$e$	${\frac {\ell }{r_{p}}}-1$	${\sqrt {1+b^{2}/a^{2}}}$
Большая полуось (<0)	$a\,\!$	$1/(2/r-v^{2}/\mu )$	$-\mu /v_{\infty }^{2}$
Гиперболическая избыточная скорость	$v_{\infty }$	${\sqrt {-\mu /a}}$
(Внешний) Угол между асимптотами	$2\theta _{\infty }$	$2\cos ^{-1}(-1/e)$	$\pi +2\tan ^{-1}(b/a)$ ^[2]
Угол между асимптотами и сопряженной осью гиперболического пути сближения	$2\nu$	$2\theta _{\infty }-\pi$	$2\sin ^{-1}{\bigg (}{\frac {1}{(1+r_{p}v_{\infty }^{2}/\mu )}}{\bigg )}$
Параметр удара ( малая полуось )	$b$	$-a{\sqrt {e^{2}-1}}$
Полупрямая сторона	$\ell$	$a(1-e^{2})$	$-b^{2}/a=h^{2}/\mu$
Расстояние периапсиса	$r_{p}$	$-a(e-1)$	${\sqrt {a^{2}+b^{2}}}+a$
Удельная орбитальная энергия	$\varepsilon$	$-\mu /2a$	$v_{\infty }^{2}/2$
Удельный угловой момент	$h$	${\sqrt {\mu \ell }}$	$bv_{\infty }$
Площадь, подметенная за раз	${\frac {\Delta A}{\Delta t}}$	${\frac {h}{2}}$

Большая полуось, энергия и гиперболическая избыточная скорость

Большая полуось ( $a\,\!$ ) не сразу виден на гиперболической траектории, но может быть построен, поскольку это расстояние от периапсиса до точки пересечения двух асимптот. Обычно, по соглашению, оно отрицательное, чтобы различные уравнения согласовывались с эллиптическими орбитами.

Большая полуось напрямую связана с удельной орбитальной энергией ( $\epsilon \,$ ) или характеристическая энергия $C_{3}$ орбиты, а скорости, которую достигает тело при стремлении расстояния к бесконечности, - гиперболическая избыточная скорость ( $v_{\infty }\,\!$ ).

v_{\infty }^{2}=2\epsilon =C_{3}=-\mu /a

или

a=-{\mu /{v_{\infty }^{2}}}

где: $\mu =Gm\,\!$ является стандартным гравитационным параметром и $C_{3}$ характерная энергия, обычно используемая при планировании межпланетных миссий.

Обратите внимание, что полная энергия положительна в случае гиперболической траектории (тогда как для эллиптической орбиты она отрицательна).

Эксцентриситет и угол между подходом и выездом

При гиперболической траектории эксцентриситет орбиты ( $e\,$ ) больше 1. Эксцентриситет напрямую связан с углом между асимптотами. При эксцентриситете чуть больше 1 гипербола имеет острую V-образную форму. В $e={\sqrt {2}}$ асимптоты расположены под прямым углом. С $e>2$ асимптоты расположены на расстоянии более 120° друг от друга, а перицентрическое расстояние больше большой полуоси. По мере дальнейшего увеличения эксцентриситета движение приближается к прямой линии.

Угол между направлением периапсиса и асимптотой центрального тела является истинной аномалией, поскольку расстояние стремится к бесконечности ( $\theta _{\infty }\,$ ), так $2\theta _{\infty }\,$ — внешний угол между направлениями подхода и ухода (между асимптотами). Затем

\theta {_{\infty }}=\cos ^{-1}(-1/e)\,

или

e=-1/\cos \theta {_{\infty }}\,

Параметр удара и расстояние наибольшего сближения

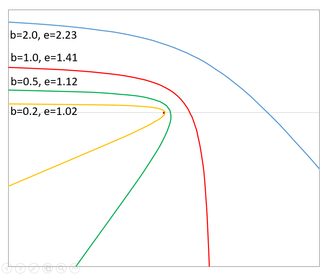
Параметр удара — это расстояние, на котором тело, если бы оно продолжало двигаться по невозмущенной траектории, пропустило бы центральное тело при его максимальном приближении . Для тел, испытывающих гравитационные силы и следующих по гиперболическим траекториям, она равна малой полуоси гиперболы.

В случае приближения космического корабля или кометы к планете ударный параметр и избыточная скорость будут известны точно. Если известно центральное тело, теперь можно найти траекторию, включая то, насколько близко приближающееся тело будет находиться в перицентре. Если это меньше радиуса планеты, следует ожидать удара. Расстояние наибольшего сближения, или перицентрическое расстояние, определяется как:

r_{p}=-a(e-1)={\frac {\mu }{v_{\infty }^{2}}}\left({\sqrt {1+\left(b{\frac {v_{\infty }^{2}}{\mu }}\right)^{2}}}-1\right)

Таким образом, если комета приближается к Земле (эффективный радиус ~6400 км) со скоростью 12,5 км/с (примерная минимальная скорость приближения тела, прилетающего из внешней Солнечной системы ), чтобы избежать столкновения с Землей, параметр удара будет нуждаться в быть не менее 8600 км, или на 34% больше радиуса Земли. Чтобы избежать столкновения, телу, приближающемуся к Юпитеру (радиус 70 000 км) из внешней Солнечной системы со скоростью 5,5 км/с, параметр удара должен быть не менее 770 000 км или в 11 раз больше радиуса Юпитера.

Если масса центрального тела неизвестна, его стандартный гравитационный параметр и, следовательно, его масса могут быть определены по отклонению меньшего тела вместе с ударным параметром и скоростью приближения. Поскольку обычно все эти переменные можно определить точно, пролет космического корабля позволит получить хорошую оценку массы тела.

\mu =bv_{\infty }^{2}\tan \delta /2

где

\delta =2\theta _{\infty }-\pi

- это угол, на который меньшее тело отклоняется от прямой линии на своем пути.

Уравнения движения

Позиция

В гиперболической траектории истинная аномалия $\theta$ связано с расстоянием между вращающимися телами ( $r\,$ ) по уравнению орбиты :

r={\frac {\ell }{1+e\cdot \cos \theta }}

Связь между истинной аномалией $θ$ и эксцентрической аномалией E (альтернативно гиперболической аномалией H ) следующая: ^[3]

\cosh {E}={{\cos {\theta }+e} \over {1+e\cdot \cos {\theta }}}

или

\tan {\frac {\theta }{2}}={\sqrt {\frac {e+1}{e-1}}}\cdot \tanh {\frac {E}{2}}

или

\tanh {\frac {E}{2}}={\sqrt {\frac {e-1}{e+1}}}\cdot \tan {\frac {\theta }{2}}

Эксцентрическая аномалия E связана со средней аномалией M уравнением Кеплера :

M=e\sinh E-E

Средняя аномалия пропорциональна времени

M={\sqrt {\frac {\mu }{-a^{3}}}}.(t-\tau ),

где μ — гравитационный параметр , а — большая полуось орбиты.

Угол траектории полета

Угол траектории полета (φ) — это угол между направлением скорости и перпендикуляром к радиальному направлению, поэтому он равен нулю в перицентре и стремится к 90 градусам на бесконечности.

\tan(\phi )={\frac {e\cdot \sin \theta }{1+e\cdot \cos \theta }}

Скорость

При стандартных предположениях орбитальная скорость ( $v\,$ ) тела, движущегося по гиперболической траектории, можно вычислить из vis-viva уравнения как:

v={\sqrt {\mu \left({2 \over {r}}+{1 \over {a}}\right)}}

^[4]

где:

$\mu \,$ стандартный гравитационный параметр ,
$r\,$ — радиальное расстояние вращающегося тела от центрального тела ,
$a\,\!$ — (отрицательная) большая полуось .

При стандартных предположениях в любом положении орбиты для орбитальной скорости справедливо соотношение ( $v\,$ ), локальная скорость убегания ( ${v_{esc}}\,$ ) и гиперболическую избыточную скорость ( $v_{\infty }\,\!$ ):

v^{2}={v_{esc}}^{2}+{v_{\infty }}^{2}

Обратите внимание: это означает, что относительно небольшая дополнительная дельта- v выше той, которая необходима для ускорения до скорости убегания, приводит к относительно большой скорости на бесконечности. Например, в месте, где скорость убегания равна 11,2 км/с, добавление 0,4 км/с дает гиперболическую избыточную скорость 3,02 км/с.

{\sqrt {11.6^{2}-11.2^{2}}}=3.02

Это пример эффекта Оберта . Обратное также верно: тело не нужно замедлять значительно по сравнению с его гиперболической избыточной скоростью (например, за счет атмосферного сопротивления вблизи перицентра), чтобы скорость упала ниже скорости убегания и, таким образом, для того, чтобы тело было захвачено.

Радиальная гиперболическая траектория

Радиальная гиперболическая траектория — это непериодическая траектория по прямой, где относительная скорость двух объектов всегда превышает скорость убегания . Возможны два случая: тела удаляются друг от друга или навстречу друг другу. Это гиперболическая орбита с малой полуосью = 0 и эксцентриситетом = 1. Хотя эксцентриситет равен 1, это не параболическая орбита.

Отклонение с конечной сферой влияния

Более точная формула угла отклонения $\delta$ учитывая радиус сферы влияния $R_{\text{SOI}}$ отклоняющего тела, предполагая перицентр $p_{e}$ является:

\delta =2\arcsin \left({\frac {{\sqrt {1-{\frac {p_{e}}{R_{\text{SOI}}}}}}{\sqrt {1+{\frac {p_{e}}{R_{\text{SOI}}}}-{\frac {2\mu p_{e}}{v_{\infty }^{2}R_{\text{SOI}}^{2}}}}}}{1+{\frac {v_{\infty }^{2}p_{e}}{\mu }}-{\frac {2p_{e}}{R_{\text{SOI}}}}}}\right)

Релятивистская задача двух тел

В контексте проблемы двух тел в общей теории относительности траектории объектов, обладающих достаточной энергией, чтобы избежать гравитационного притяжения другого, больше не имеют формы гиперболы. Тем не менее, термин «гиперболическая траектория» до сих пор используется для описания орбит такого типа.

См. также

Ссылки

Валладо, Дэвид А. (2007). Основы астродинамики и приложения, третье издание . Хоторн, Калифорния: Хоторн Пресс. ISBN 978-1-881883-14-2 .

^ ТАК, Кеплер; Сарайва, Мария де Фатима (2014). Астрономия и астрофизика . Порту-Алегри: Кафедра астрономии - Институт физики Федерального университета Риу-Гранди-ду-Сул, стр. 97–106.
^ «Основы космического полета: орбитальная механика» . Архивировано из оригинала 4 февраля 2012 г. Проверено 28 февраля 2012 г.
^ Пит, Мэтью М. (13 июня 2019 г.). «Динамика и управление космическим кораблем» (PDF) .
^ Орбитальная механика и астродинамика Брайана Вебера: https://orbital-mechanics.space/the-orbit-equation/hyperbolic-trajectories.html

Внешние ссылки

[1] ТАК, Кеплер; Сарайва, Мария де Фатима (2014). Астрономия и астрофизика . Порту-Алегри: Кафедра астрономии - Институт физики Федерального университета Риу-Гранди-ду-Сул, стр. 97–106.

[2] «Основы космического полета: орбитальная механика» . Архивировано из оригинала 4 февраля 2012 г. Проверено 28 февраля 2012 г.

[3] Пит, Мэтью М. (13 июня 2019 г.). «Динамика и управление космическим кораблем» (PDF) .

[4] Орбитальная механика и астродинамика Брайана Вебера: https://orbital-mechanics.space/the-orbit-equation/hyperbolic-trajectories.html

[1]

[2]

[3]

[4]