Уравнение ракеты Циолковского

Классическое уравнение ракеты , или уравнение идеальной ракеты, представляет собой математическое уравнение, описывающее движение транспортных средств, которое следует основному принципу ракеты : устройство, которое может придавать себе ускорение, используя тягу , выбрасывая часть своей массы с высокой скоростью и тем самым может двигаться за счет сохранения импульса .Приписывается Константину Циолковскому , который независимо вывел его и опубликовал в 1903 году. ^[1]^[2] хотя он был независимо получен и опубликован Уильямом Муром в 1810 году, ^[3] и позже опубликовано в отдельной книге в 1813 году. ^[4] Роберт Годдард также разработал его независимо в 1912 году, а Герман Оберт независимо вывел его примерно в 1920 году.

Максимальное изменение скорости автомобиля, $\Delta v$ (без действия внешних сил):

$\Delta v=v_{\text{e}}\ln {\frac {m_{0}}{m_{f}}}=I_{\text{sp}}g_{0}\ln {\frac {m_{0}}{m_{f}}},$ где:

$v_{\text{e}}=I_{\text{sp}}g_{0}$ $v_{\text{e}}=I_{\text{sp}}g_{0}$ – эффективная скорость истечения ;
- $I_{\text{sp}}$ – удельный импульс в измерении времени;
- $g_{0}$ стандартная гравитация ;
$\ln$ – функция натурального логарифма ;
$m_{0}$ — начальная общая масса, включая топливо , т. е. влажная масса;
$m_{f}$ — это конечная общая масса без топлива, т. е. сухая масса.

Учитывая эффективную скорость выхлопа, определяемую конструкцией ракетного двигателя, желаемую дельта-v (например, орбитальную скорость или скорость убегания ) и заданную сухую массу. $m_{f}$ , уравнение можно решить для требуемой массы пороха $m_{0}-m_{f}$ : $m_{0}=m_{f}e^{\Delta v/v_{\text{e}}}.$

Необходимая влажная масса растет в геометрической прогрессии с желаемой дельтой-v.

История

Уравнение названо в честь русского учёного Константина Циолковского , который независимо вывел его и опубликовал в своей работе 1903 года. ^[5]^[2]

Уравнение было получено ранее британским математиком Уильямом Муром в 1810 году. ^[3] и позже опубликовано в отдельной книге в 1813 году. ^[4]

Американец Роберт Годдард независимо разработал это уравнение в 1912 году, когда начал исследования по улучшению ракетных двигателей для возможных космических полетов. Немецкий инженер Герман Оберт независимо вывел уравнение примерно в 1920 году, изучая возможность космических путешествий.

Хотя вывод уравнения ракеты представляет собой простое вычислительное упражнение, Циолковский удостоен чести быть первым, кто применил его к вопросу о том, могут ли ракеты развивать скорости, необходимые для космических путешествий .

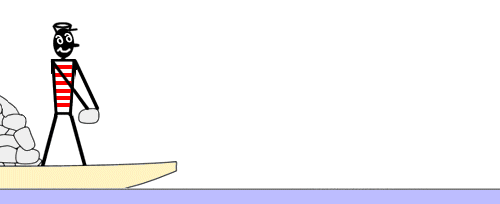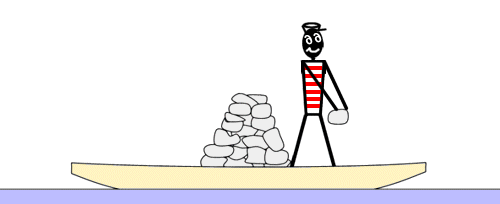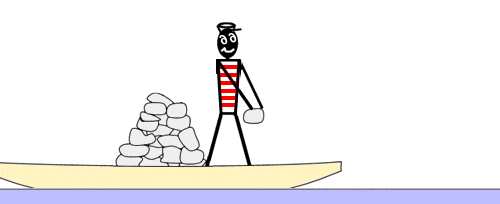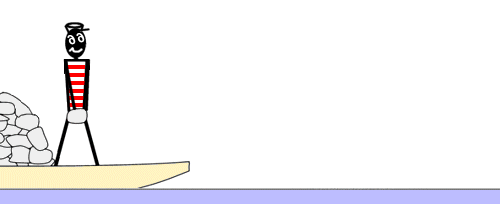
Эксперимент с лодкой Циолковского.

Чтобы понять принцип движения ракеты, Константин Циолковский предложил знаменитый эксперимент «лодочки». Человек находится в лодке вдали от берега без весел. Они хотят достичь этого берега. Они замечают, что лодка загружена некоторым количеством камней, и им приходит в голову мысль бросить по одному и как можно быстрее эти камни в сторону, противоположную берегу. Фактически количество движения камней, брошенных в одном направлении, соответствует такому же количеству движения лодки в другом направлении.

Вывод

Самый популярный вывод

Рассмотрим следующую систему:

В следующем переводе термин «ракета» понимается как «ракета и все ее неизрасходованное топливо».

Второй закон движения Ньютона связывает внешние силы ( ${\vec {F_{i}}}$ ) к изменению импульса всей системы (включая ракету и выхлоп) следующим образом: $\sum _{i}{\vec {F_{i}}}=\lim _{\Delta t\to 0}{\frac {{\vec {P_{2}}}-{\vec {P_{1}}}}{\Delta t}}$ где ${\vec {P_{1}}}$ это импульс ракеты в момент времени $t=0$ : ${\vec {P_{1}}}=m{\vec {V}}$ и ${\vec {P_{2}}}$ - импульс ракеты и отработанная масса в момент времени $t=\Delta t$ : ${\vec {P_{2}}}=\left(m-\Delta m\right)\left({\vec {V}}+\Delta {\vec {V}}\right)+\Delta m{\vec {V_{\text{e}}}}$ и где по отношению к наблюдателю:

${\vec {V}}$ это скорость ракеты в момент времени $t=0$
${\vec {V}}+\Delta {\vec {V}}$ это скорость ракеты в момент времени $t=\Delta t$
${\vec {V_{\text{e}}}}$ - это скорость массы, добавляемой к выхлопу (и теряемой ракетой) за время $\Delta t$
$m$ это масса ракеты в момент времени $t=0$
$\left(m-\Delta m\right)$ это масса ракеты в момент времени $t=\Delta t$

Скорость выхлопа ${\vec {V_{\text{e}}}}$ в системе наблюдателя связана со скоростью выхлопа в системе координат ракеты $v_{\text{e}}$ к: ${\vec {v_{\text{e}}}}={\vec {V_{\text{e}}}}-{\vec {V}}$ таким образом, ${\vec {V_{\text{e}}}}={\vec {V}}+{\vec {v_{\text{e}}}}$ Решение этого вопроса дает: ${\vec {P_{2}}}-{\vec {P_{1}}}=m\Delta {\vec {V}}+{\vec {v_{\text{e}}}}\Delta m-\Delta m\Delta {\vec {V}}$ Если ${\vec {V}}$ и ${\vec {v_{\text{e}}}}$ противоположны, ${\vec {F_{\text{i}}}}$ иметь то же направление, что и ${\vec {V}}$ , $\Delta m\Delta {\vec {V}}$ пренебрежимо малы (поскольку $dmd{\vec {v}}\rightarrow 0$ ), и используя $dm=-\Delta m$ (с момента выброса положительного $\Delta m$ приводит к уменьшению массы ракеты во времени), $\sum _{i}F_{i}=m{\frac {dV}{dt}}+v_{\text{e}}{\frac {dm}{dt}}$

Если внешних сил нет, то ${\textstyle \sum _{i}F_{i}=0}$ ( сохранение импульса ) и $-m{\frac {dV}{dt}}=v_{\text{e}}{\frac {dm}{dt}}$

Предполагая, что $v_{\text{e}}$ постоянна (известна как гипотеза Циолковского ^[2]), поэтому оно не подлежит интегрированию, то приведенное выше уравнение можно проинтегрировать следующим образом: $-\int _{V}^{V+\Delta V}\,dV={v_{e}}\int _{m_{0}}^{m_{f}}{\frac {dm}{m}}$

Тогда это дает $\Delta V=v_{\text{e}}\ln {\frac {m_{0}}{m_{f}}}$ или эквивалентно $m_{f}=m_{0}e^{-\Delta V\ /v_{\text{e}}}$ или $m_{0}=m_{f}e^{\Delta V/v_{\text{e}}}$ или $m_{0}-m_{f}=m_{f}\left(e^{\Delta V/v_{\text{e}}}-1\right)$ где $m_{0}$ - начальная общая масса, включая топливо, $m_{f}$ конечная масса и $v_{\text{e}}$ скорость истечения ракеты относительно ракеты ( удельный импульс или, если измерять во времени, умноженный на ускорение силы тяжести на Земле). Если $v_{\text{e}}$ НЕ является константой, у нас может не быть таких простых уравнений ракеты, как приведенные выше формы. Многие исследования ракетной динамики основывались на постоянной Циолковского. $v_{\text{e}}$ гипотеза.

Значение $m_{0}-m_{f}$ – общая рабочая масса израсходованного топлива.

$\Delta V$ ( дельта v ) — это интегрирование во времени величины ускорения, создаваемого ракетным двигателем (каким было бы фактическое ускорение, если бы внешние силы отсутствовали). В свободном пространстве для случая ускорения по направлению скорости – это увеличение скорости. В случае ускорения в противоположном направлении (замедления) – это уменьшение скорости. Конечно, гравитация и сопротивление также ускоряют транспортное средство и могут увеличивать или уменьшать изменение скорости, испытываемое транспортным средством. Следовательно, дельта-v не всегда может быть фактическим изменением скорости или скорости транспортного средства.

Другие производные

Импульсный

Уравнение также можно вывести из основного интеграла ускорения в виде силы (тяги) по массе.Представляя уравнение дельта-v следующим образом: $\Delta v=\int _{t_{0}}^{t_{f}}{\frac {|T|}{{m_{0}}-{t}\Delta {m}}}~dt$

где Т — тяга, $m_{0}$ - начальная (влажная) масса и $\Delta m$ - начальная масса минус конечная (сухая) масса,

и понимая, что интеграл результирующей силы с течением времени представляет собой полный импульс, предполагая, что тяга является единственной задействованной силой, $\int _{t_{0}}^{t_{f}}F~dt=J$

Интеграл оказывается: $J~{\frac {\ln({m_{0}})-\ln({m_{f}})}{\Delta m}}$

Понимая, что импульс изменения массы эквивалентен силе, воздействующей на массовый расход топлива (p), который сам по себе эквивалентен скорости истечения, ${\frac {J}{\Delta m}}={\frac {F}{p}}=V_{\text{exh}}$ интеграл можно приравнять $\Delta v=V_{\text{exh}}~\ln \left({\frac {m_{0}}{m_{f}}}\right)$

На основе ускорения

Представьте себе ракету, покоящуюся в космосе, на которую не действуют никакие силы ( Первый закон движения Ньютона ). С момента запуска двигателя (часы установлены на 0) ракета выбрасывает массу газа с постоянным массовым расходом R (кг/с) и скоростью истечения относительно ракеты v _e (м/с). Это создает постоянную силу F, приводящую в движение ракету, равную R × v _e . На ракету действует постоянная сила, но ее общая масса постоянно уменьшается, поскольку она выбрасывает газ. Согласно Второму закону движения Ньютона , его ускорение в любой момент времени t равно его движущей силе F, деленной на его текущую массу m : $~a={\frac {dv}{dt}}=-{\frac {F}{m(t)}}=-{\frac {Rv_{\text{e}}}{m(t)}}$

Теперь масса топлива, изначально находящегося на борту ракеты, равна m ₀ – m _f . Следовательно, при постоянном массовом расходе R потребуется время T = ( m ₀ – m _f )/ R , чтобы сжечь все это топливо. Интегрируя обе части уравнения по времени от 0 до T (и отмечая, что R = dm/dt допускает замену справа), получаем: $~\Delta v=v_{f}-v_{0}=-v_{\text{e}}\left[\ln m_{f}-\ln m_{0}\right]=~v_{\text{e}}\ln \left({\frac {m_{0}}{m_{f}}}\right).$

Предел выброса «пеллеты» конечной массы

Уравнение ракеты также можно вывести как предельный случай изменения скорости ракеты, выбрасывающей топливо в виде $N$ гранулы последовательно, так как $N\to \infty$ , с эффективной скоростью выхлопа $v_{\text{eff}}$ так что механическая энергия, полученная на единицу массы топлива, определяется выражением ${\textstyle {\tfrac {1}{2}}v_{\text{eff}}^{2}}$ .

В системе центра масс ракеты, если шарик массой $m_{p}$ выбрасывается со скоростью $u$ а оставшаяся масса ракеты равна $m$ , количество энергии, преобразуемой в увеличение кинетической энергии ракеты и пули, равно ${\tfrac {1}{2}}m_{p}v_{\text{eff}}^{2}={\tfrac {1}{2}}m_{p}u^{2}+{\tfrac {1}{2}}m(\Delta v)^{2}.$

Используя сохранение импульса в корпусе ракеты непосредственно перед выбросом, ${\textstyle u=\Delta v{\tfrac {m}{m_{p}}}}$ , из чего находим $\Delta v=v_{\text{eff}}{\frac {m_{p}}{\sqrt {m(m+m_{p})}}}.$

Позволять $\phi$ быть исходной массовой долей топлива на борту и $m_{0}$ начальная заправленная масса ракеты. Разделите общую массу топлива $\phi m_{0}$ в $N$ дискретные гранулы, каждая массой $m_{p}=\phi m_{0}/N$ . Оставшаяся масса ракеты после катапультирования $j$ тогда пеллеты $m=m_{0}(1-j\phi /N)$ . Общее изменение скорости после выброса $j$ пеллеты это сумма ^[6] $\Delta v=v_{\text{eff}}\sum _{j=1}^{j=N}{\frac {\phi /N}{\sqrt {(1-j\phi /N)(1-j\phi /N+\phi /N)}}}$

Обратите внимание, что для больших $N$ последнее слагаемое в знаменателе $\phi /N\ll 1$ и им можно пренебречь, чтобы дать $\Delta v\approx v_{\text{eff}}\sum _{j=1}^{j=N}{\frac {\phi /N}{1-j\phi /N}}=v_{\text{eff}}\sum _{j=1}^{j=N}{\frac {\Delta x}{1-x_{j}}}$ где ${\textstyle \Delta x={\frac {\phi }{N}}}$ и ${\textstyle x_{j}={\frac {j\phi }{N}}}$ .

Как $N\rightarrow \infty$ эта сумма Римана становится определенным интегралом $\lim _{N\to \infty }\Delta v=v_{\text{eff}}\int _{0}^{\phi }{\frac {dx}{1-x}}=v_{\text{eff}}\ln {\frac {1}{1-\phi }}=v_{\text{eff}}\ln {\frac {m_{0}}{m_{f}}},$ поскольку конечная оставшаяся масса ракеты равна $m_{f}=m_{0}(1-\phi )$ .

Специальная теория относительности

Если принять во внимание специальную теорию относительности можно вывести следующее уравнение , для релятивистской ракеты : ^[7] с $\Delta v$ снова означает конечную скорость ракеты (после выброса всей ее реакционной массы и уменьшения ее до массы покоя $m_{1}$ ) в инерциальной системе отсчета , где ракета стартовала в состоянии покоя (масса покоя, включая топливо, равна $m_{0}$ изначально) и $c$ что означает скорость света в вакууме: ${\frac {m_{0}}{m_{1}}}=\left[{\frac {1+{\frac {\Delta v}{c}}}{1-{\frac {\Delta v}{c}}}}\right]^{\frac {c}{2v_{\text{e}}}}$

Письмо ${\textstyle {\frac {m_{0}}{m_{1}}}}$ как $R$ позволяет переписать это уравнение в виде ${\frac {\Delta v}{c}}={\frac {R^{\frac {2v_{\text{e}}}{c}}-1}{R^{\frac {2v_{\text{e}}}{c}}+1}}$

Затем, используя тождество ${\textstyle R^{\frac {2v_{\text{e}}}{c}}=\exp \left[{\frac {2v_{\text{e}}}{c}}\ln R\right]}$ (здесь «exp» обозначает показательную функцию ; см. также Натуральный логарифм , а также «степенное» тождество в логарифмических тождествах ) и тождество ${\textstyle \tanh x={\frac {e^{2x}-1}{e^{2x}+1}}}$ ( см. Гиперболическую функцию ), это эквивалентно $\Delta v=c\tanh \left({\frac {v_{\text{e}}}{c}}\ln {\frac {m_{0}}{m_{1}}}\right)$

Члены уравнения

Delta- v

Дельта- v (буквально « изменение скорости , »), обозначаемая как Δ v и произносится как дельта-vee используемая в динамике полета космического корабля , является мерой импульса , необходимого для выполнения маневра, такого как запуск или приземление на планета или луна, или орбитальный маневр в космосе . Это скаляр , имеющий единицы скорости . В данном контексте это не то же самое, что физическое изменение скорости транспортного средства.

Дельта- v создается реактивными двигателями, такими как ракетные двигатели , пропорциональна тяге на единицу массы и времени горения и используется для определения массы топлива, необходимой для данного маневра, через уравнение ракеты.

Для нескольких маневров дельта- v суммируется линейно.

Для межпланетных миссий дельта- v часто отображается на графике , который отображает требуемую дельту- v миссии как функцию даты запуска.

Массовая доля

В аэрокосмической технике массовая доля топлива — это часть массы транспортного средства, которая не достигает пункта назначения, обычно используемая в качестве меры производительности транспортного средства. Другими словами, массовая доля топлива — это отношение массы топлива к начальной массе транспортного средства. Для космического корабля пунктом назначения обычно является орбита, а для самолетов — место приземления. Более высокая массовая доля означает меньший вес конструкции. Другой связанной мерой является доля полезной нагрузки , которая представляет собой долю первоначального веса, составляющую полезную нагрузку.

Эффективная скорость выхлопа

Эффективная скорость выхлопа часто определяется как удельный импульс , и они связаны друг с другом следующим образом: $v_{\text{e}}=g_{0}I_{\text{sp}},$ где

$I_{\text{sp}}$ – удельный импульс в секундах,
$v_{\text{e}}$ — удельный импульс, измеренный в м/с , который совпадает с эффективной скоростью выхлопа, измеренной в м/с (или фут/с, если g выражено в фут/с). ²),
$g_{0}$ — стандартная сила тяжести , 9,80665 м/с. ² (в британских единицах 32,174 фута/с ²).

Применимость

Уравнение ракеты отражает основы физики полета ракеты в одном коротком уравнении. Это также справедливо для ракетоподобных реактивных транспортных средств, когда эффективная скорость выхлопа постоянна, и может суммироваться или интегрироваться, когда эффективная скорость выхлопа меняется. Уравнение ракеты учитывает только силу реакции ракетного двигателя; он не включает другие силы, которые могут действовать на ракету, такие как аэродинамические или гравитационные силы. Таким образом, при использовании его для расчета потребности в топливе для запуска с планеты с атмосферой (или механического спуска на нее) эффекты этих сил должны быть включены в требование дельта-V (см. Примеры ниже). В так называемом «тирании ракетного уравнения» существует ограничение на количество полезной нагрузки , которую может нести ракета, поскольку большее количество топлива увеличивает общий вес и, таким образом, также увеличивает расход топлива. ^[8] Уравнение не применимо к неракетным системам, таким как аэродинамическое торможение , артиллерийские пуски , космические лифты , стартовые петли , тросовые двигательные установки или легкие паруса .

Уравнение ракеты можно применять к орбитальным маневрам, чтобы определить, сколько топлива необходимо для перехода на определенную новую орбиту или для нахождения новой орбиты в результате определенного сгорания топлива. При применении орбитальных маневров предполагается импульсный маневр , при котором топливо выбрасывается и мгновенно применяется дельта-v. Это предположение является относительно точным для кратковременных ожогов, например, для коррекций на середине курса и маневров по выведению на орбиту. По мере увеличения продолжительности горения результат становится менее точным из-за воздействия силы тяжести на транспортное средство во время маневра. Для малой тяги и длительного движения, такого как электрическое движение , для прогнозирования орбитального движения используется более сложный анализ, основанный на распространении вектора состояния космического корабля и интегрировании тяги.

Примеры

Предположим, что скорость выхлопа равна 4500 метров в секунду (15000 футов/с) и $\Delta v$ 9700 метров в секунду (32000 футов/с) (от Земли до НОО , включая $\Delta v$ преодолевать гравитацию и аэродинамическое сопротивление).

Одноступенчатая ракета для вывода на орбиту: $1-e^{-9.7/4.5}$ = 0,884, следовательно, 88,4% от начальной общей массы должно составлять топливо. Остальные 11,6% приходится на двигатели, танк и полезную нагрузку.
Двухступенчатый вывод на орбиту : предположим, что первая ступень должна обеспечивать $\Delta v$ 5000 метров в секунду (16000 футов/с); $1-e^{-5.0/4.5}$ = 0,671, следовательно, 67,1% от начальной общей массы должно приходиться на топливо первой ступени. Оставшаяся масса составляет 32,9%. После утилизации первой ступени масса остается равной этим 32,9% за вычетом массы танка и двигателей первой ступени. Предположим, что это 8% от первоначальной общей массы, тогда останется 24,9%. Второй этап должен обеспечить $\Delta v$ 4700 метров в секунду (15 000 футов/с); $1-e^{-4.7/4.5}$ = 0,648, следовательно, 64,8% оставшейся массы должно составлять топливо, что составляет 16,2% от первоначальной общей массы, а 8,7% остается на бак и двигатели второй ступени, на полезную нагрузку, а в случае с космическим челноком , а также орбитальный аппарат. в совокупности доступно 16,7% исходной стартовой массы . Таким образом, для всех двигателей, баков и полезной нагрузки

Этапы

В случае последовательных ступеней ракеты уравнение применяется для каждой ступени, где для каждой ступени начальная масса в уравнении представляет собой полную массу ракеты после отказа от предыдущей ступени, а конечная масса в уравнении представляет собой полную массу. ракеты непосредственно перед выбросом соответствующей ступени. Для каждого этапа удельный импульс может быть разным.

Например, если 80% массы ракеты составляет топливо первой ступени, 10% — сухая масса первой ступени и 10% — остальная ракета, то

${\begin{aligned}\Delta v\ &=v_{\text{e}}\ln {100 \over 100-80}\\&=v_{\text{e}}\ln 5\\&=1.61v_{\text{e}}.\\\end{aligned}}$

С тремя одинаковыми, впоследствии меньшими ступенями с одинаковыми $v_{\text{e}}$ для каждого этапа дает:

$\Delta v\ =3v_{\text{e}}\ln 5\ =4.83v_{\text{e}}$

а полезная нагрузка составляет 10% × 10% × 10% = 0,1% от начальной массы.

Сопоставимая ракета SSTO , также с полезной нагрузкой 0,1%, могла бы иметь массу топливных баков и двигателей 11,1% и топлива 88,8%. Это дало бы

$\Delta v\ =v_{\text{e}}\ln(100/11.2)\ =2.19v_{\text{e}}.$

Если двигатель новой ступени зажигается до того, как была сброшена предыдущая ступень и одновременно работающие двигатели имеют разный удельный импульс (как это часто бывает с твердотопливными ракетными ускорителями и жидкотопливной ступенью), ситуация усложняется.

См. также

Delta-v budget
Проблема с джипом
Соотношение масс
Эффект Оберта — применение дельта-v в гравитационной скважине увеличивает конечную скорость.
Релятивистская ракета
Обратимость орбит
Роберт Х. Годдард - добавлены термины для гравитации и сопротивления в вертикальном полете.
Движение космического корабля
Закон эпонимии Стиглера

Ссылки

^ К. Ціолковскій, Изслѣдованіе мировыхъ пространствъ реактивными приборами, 1903 (available online here Archived 2011-08-15 at the Wayback Machine in a RARed PDF)
↑ Перейти обратно: Перейти обратно: ^а ^б ^с Циолковский, К. «Реактивные летательные аппараты» (PDF) .
↑ Перейти обратно: Перейти обратно: ^а ^б Мур, Уильям (1810). «О движении ракет как в несопротивляющихся, так и в сопротивляющихся средах» . Журнал естественной философии, химии и искусств . 27 : 276–285.
↑ Перейти обратно: Перейти обратно: ^а ^б Мур, Уильям (1813). «Трактат о движении ракет», к которому добавлен «Очерк морской артиллерийской стрельбы в теории и практике» и т. д . Г. и С. Робинсоны.
^ К. Ціолковскій, Изслѣдованіе мировыхъ пространствъ реактивными приборами, 1903 (available online here Archived 2011-08-15 at the Wayback Machine in a RARed PDF)
^ Бланко, Филип (ноябрь 2019 г.). «Дискретный, энергетический подход к ракетному движению». Физическое образование . 54 (6): 065001. Бибкод : 2019PhyEd..54f5001B . дои : 10.1088/1361-6552/ab315b . S2CID 202130640 .
^ Вперед, Роберт Л. «Прозрачный вывод уравнения релятивистской ракеты» (см. правую часть уравнения 15 на последней странице, где R — это отношение начальной к конечной массе, а w — скорость истечения, соответствующая v _e в обозначениях этой статьи)
^ «Тирания ракетного уравнения» . НАСА.gov . Архивировано из оригинала 06 марта 2022 г. Проверено 18 апреля 2016 г.

Внешние ссылки

[1] К. Ціолковскій, Изслѣдованіе мировыхъ пространствъ реактивными приборами, 1903 (available online here Archived 2011-08-15 at the Wayback Machine in a RARed PDF)

[ReactiveFlyingMachines-2] Перейти обратно: Перейти обратно: ^а ^б ^с Циолковский, К. «Реактивные летательные аппараты» (PDF) .

[moore1810-3] Перейти обратно: Перейти обратно: ^а ^б Мур, Уильям (1810). «О движении ракет как в несопротивляющихся, так и в сопротивляющихся средах» . Журнал естественной философии, химии и искусств . 27 : 276–285.

[moore-4] Перейти обратно: Перейти обратно: ^а ^б Мур, Уильям (1813). «Трактат о движении ракет», к которому добавлен «Очерк морской артиллерийской стрельбы в теории и практике» и т. д . Г. и С. Робинсоны.

[5] К. Ціолковскій, Изслѣдованіе мировыхъ пространствъ реактивными приборами, 1903 (available online here Archived 2011-08-15 at the Wayback Machine in a RARed PDF)

[discreteproof-6] Бланко, Филип (ноябрь 2019 г.). «Дискретный, энергетический подход к ракетному движению». Физическое образование . 54 (6): 065001. Бибкод : 2019PhyEd..54f5001B . дои : 10.1088/1361-6552/ab315b . S2CID 202130640 .

[7] Вперед, Роберт Л. «Прозрачный вывод уравнения релятивистской ракеты» (см. правую часть уравнения 15 на последней странице, где R — это отношение начальной к конечной массе, а w — скорость истечения, соответствующая v _e в обозначениях этой статьи)

[8] «Тирания ракетного уравнения» . НАСА.gov . Архивировано из оригинала 06 марта 2022 г. Проверено 18 апреля 2016 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]