Экспоненциальная функция

Эта статья о функции f ( x ) = e ^Икс и его обобщения. Для функций вида f ( x ) = x ^р , см. функцию мощности . Для двумерной функции f ( x , y ) = x ^и см. Возведение в степень . Для представления научных чисел см обозначение E. .

Экспоненциальный
Естественная показательная функция вдоль части действительной оси
Общая информация
Общее определение	$\exp z=e^{z}$
Домен, кодомен и изображение
Домен	$\mathbb {C}$
Изображение	${\begin{cases}(0,\infty )&{\text{for }}z\in \mathbb {R} \\\mathbb {C} \setminus \{0\}&{\text{for }}z\in \mathbb {C} \end{cases}}$
Конкретные значения
На нуле	1
Значение в 1	Это
Особенности
Фиксированная точка	− W n (−1) для $n\in \mathbb {Z}$
Связанные функции
Взаимный	$\exp(-z)$
Обратный	Натуральный логарифм , Комплексный логарифм
Производная	$\exp 'z=\exp z$
Первообразная	$\int \exp z\,dz=\exp z+C$
Определение серии
Серия Тейлора	$\exp z=\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}}$

Показательные функции с основаниями 2 и 1/2

Показательная функция — это математическая функция , обозначаемая $f(x)=\exp(x)$ или $e^{x}$(где аргумент x записан как показатель степени ). Если не указано иное, этот термин обычно относится к положительной функции действительной переменной , хотя его можно распространить на комплексные числа или обобщить на другие математические объекты, такие как матрицы или алгебры Ли . Показательная функция возникла из операции степень возведения числа в (многократного умножения), но различные современные определения позволяют строго распространить ее на все действительные аргументы. $x$, включая иррациональные числа . Ее повсеместное появление в чистой и прикладной математике побудило математика Вальтера Рудина считать показательную функцию «самой важной функцией в математике».

Функции $f(x)=b^{x}$ для положительных действительных чисел $b$ также известны как показательные функции и удовлетворяют тождеству возведения в степень :

$$b^{x+y}=b^{x}b^{y}{\text{ for all }}x,y\in \mathbb {R} .$$

Из этого следует $b^{n}=b\times \cdots \times b$ (с $n$ коэффициенты) для положительных целых чисел $n$, где $b=b^{1}$, связывая показательные функции с элементарным понятием возведения в степень. Натуральная основа $e=\exp(1)=2.71828\ldots$— это вездесущая математическая константа , называемая числом Эйлера . Чтобы отличить его, $\exp(x)=e^{x}$ называется экспоненциальной функцией или естественной экспоненциальной функцией : это уникальная функция действительной переменной, производная которой равна самой себе и значение которой в точке 0 равно 1 :

$\exp '(x)=\exp(x)$ для всех $x\in \mathbb {R}$, и $\exp(0)=1.$

Отношение $b^{x}=e^{x\ln b}$ для $b>0$ и реальный или сложный $x$ позволяет выражать общие показательные функции через естественную показательную функцию.

В более общем плане, особенно в прикладных настройках, любая функция $f:\mathbb {R} \to \mathbb {R}$ определяется

$$f(x)=ce^{ax}=cb^{kx},{\text{ with }}k=a/\ln b,\ a\neq 0,\ b,c>0$$

также известна как экспоненциальная функция, поскольку она решает задачу начального значения $f'=af,\ f(0)=c$, что означает, что скорость изменения в каждой точке пропорциональна значению функции в этой точке. Такое поведение моделирует различные явления в биологических, физических и социальных науках, например, неограниченный рост , самовоспроизводящегося населения распад радиоактивного элемента , сложные проценты , начисляемые на финансовый фонд, или растущий объем производственных знаний. .

Действительная показательная функция также может быть определена как степенной ряд , который легко расширяется до комплексных аргументов для определения комплексной показательной функции. $\exp :\mathbb {C} \to \mathbb {C}$. Эта функция принимает все комплексные значения, кроме 0, и тесно связана с комплексными тригонометрическими функциями , как показывает формула Эйлера :

$e^{x+iy}=e^{x}\cos(y)\,+\,i\,e^{x}\sin(y).$

Благодаря своим более абстрактным свойствам и характеристикам экспоненциальная функция может быть обобщена на гораздо более широкие контексты, такие как квадратные матрицы и группы Ли . Более того, определение дифференциального уравнения можно обобщить на риманово многообразие .

Действительная показательная функция является биекцией из $\mathbb {R}$ к интервалу $(0,\infty )$. Его обратной функцией является натуральный логарифм , обозначаемый $\ln$, $\log$, или $\log _{e}$и некоторые старые тексты назвал его антилогарифмом .

График

График ​ ​ $y=e^{x}$ имеет восходящий наклон и увеличивается быстрее с увеличением x . График всегда лежит выше оси x , но становится сколь угодно близким к ней при больших отрицательных x ; таким образом, ось x является горизонтальной асимптотой . Уравнение ${\tfrac {d}{dx}}e^{x}=e^{x}$ означает, что наклон касательной к графику в каждой точке равен ее координате y в этой точке.

Отношение к более общим экспоненциальным функциям

Показательная функция $f(x)=e^{x}$иногда называют естественной показательной функцией , чтобы отличить ее от других показательных функций. Изучение любой показательной функции можно легко свести к изучению естественной показательной функции, поскольку по определению для b положительного

$$b^{x}\mathrel {\stackrel {\text{def}}{=}} e^{x\ln b}$$

Как функции действительной переменной показательные функции однозначно характеризуются тем, что производная такой функции прямо пропорциональна значению функции. Константа пропорциональности этого отношения представляет собой натуральный логарифм по основанию b :

$${\frac {d}{dx}}b^{x}={\frac {d}{dx}}e^{x\ln(b)}=e^{x\ln(b)}\ln(b)=b^{x}\ln(b).$$

Для b > 1 функция $b^{x}$ увеличивается (как показано для b = e и b = 2 ), потому что $\ln b>0$делает производную всегда положительной; это часто называют экспоненциальным ростом . При положительном b < 1 функция убывает (как показано для b = 1/2 ​ ) ; это часто называют экспоненциальным затуханием . Для b = 1 функция постоянна.

Число Эйлера е = 2,71828... является единственной базой, для которой константа пропорциональности равна 1, поскольку $\ln(e)=1$, так что функция является собственной производной:

$${\frac {d}{dx}}e^{x}=e^{x}\ln(e)=e^{x}.$$

Эта функция, также обозначаемая как exp x , называется «естественной экспоненциальной функцией». или просто «показательная функция». Поскольку любая показательная функция, определяемая формулой $f(x)=b^{x}$ можно записать в терминах натуральной экспоненты как $b^{x}=e^{x\ln b}$, вычислительно и концептуально удобно свести исследование показательных функций именно к этой. Поэтому естественная экспонента обозначается через

$$x\mapsto e^{x}$$

или

$$x\mapsto \exp x.$$

Первое обозначение обычно используется для более простых показателей степени, тогда как второе предпочтительнее, когда показатель степени более сложный и его труднее читать, набранный мелким шрифтом.

Для действительных чисел c и d функция вида $f(x)=ab^{cx+d}$ также является показательной функцией, поскольку ее можно переписать как

$$ab^{cx+d}=\left(ab^{d}\right)\left(b^{c}\right)^{x}.$$

Формальное определение

Основная статья: Характеристики показательной функции

Показательная функция (синим цветом) и сумма первых n + 1 членов ее степенного ряда (красным цветом)

Действительная показательная функция $\exp :\mathbb {R} \to \mathbb {R}$можно охарактеризовать множеством эквивалентных способов. Обычно его определяют следующим степенным рядом :

$$\exp x:=\sum _{k=0}^{\infty }{\frac {x^{k}}{k!}}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+\cdots$$

Поскольку радиус сходимости этого степенного ряда бесконечен, это определение фактически применимо ко всем комплексным числам; см. § Комплексную плоскость для продолжения $\exp x$на комплексную плоскость. Используя степенной ряд, константу e можно определить как ${\textstyle e=\exp 1=\sum _{k=0}^{\infty }(1/k!)\,.}$

Почленное дифференцирование этого степенного ряда показывает, что ${\textstyle {\frac {d}{dx}}\exp x=\exp x}$ для всех действительных x , что приводит к другой общей характеристике $\exp x$ как единственное решение дифференциального уравнения

$$y'(x)=y(x)$$

который удовлетворяет начальному условию $y(0)=1.$

Основываясь на этой характеристике, цепное правило показывает, что его обратная функция, натуральный логарифм , удовлетворяет условию ${\textstyle {\frac {d}{dy}}\ln y=1/y}$ для $y>0,$ или ${\textstyle \ln y=\int _{1}^{y}{\frac {dt}{t}}\,.}$ Эта связь приводит к менее распространенному определению действительной показательной функции. $\exp(x)$ как решение $y$ к уравнению

$$x=\int _{1}^{y}{\frac {1}{t}}\,dt.$$

Решение обыкновенного дифференциального уравнения $y'(x)=y(x)$ с начальным состоянием $y'(0)=1$ использование метода Эйлера дает формулу предела продукта, действительную для всех комплексных значений $x$:

$$\exp x=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}.$$

Можно показать, что каждое непрерывное ненулевое решение функционального уравнения $f(x+y)=f(x)f(y)$ для $f:\mathbb {R} \to \mathbb {R}$ является показательной функцией, $f(x)=e^{kx}$ с $k\in \mathbb {R} .$

Обзор

Красная кривая — показательная функция. Черные горизонтальные линии показывают места пересечения зеленых вертикальных линий.

Показательная функция возникает всякий раз, когда величина растет или убывает со скоростью, пропорциональной ее текущему значению. Одной из таких ситуаций является постоянное начисление процентов , и фактически именно это наблюдение привело Якоба Бернулли в 1683 г. на номер

$$\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}$$

теперь известный как e . Позже, в 1697 году, Иоганн Бернулли изучал исчисление показательной функции.

Если основная сумма в размере 1 приносит проценты по годовой ставке x , начисляемой ежемесячно, то проценты, получаемые каждый месяц, равны x / 12 раз превышает текущее значение, поэтому каждый месяц общая стоимость умножается на (1 + x / 12 ) , а значение на конец года равно (1 + х / 12 ) ¹² . Если вместо этого проценты начисляются ежедневно, это становится (1 + х / 365 ) ³⁶⁵ . Если позволить количеству временных интервалов в году неограниченно расти, то это приведет к предельному определению показательной функции:

$$\exp x=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}$$

впервые дано Леонардом Эйлером . Это одна из многих характеристик показательной функции ; другие включают ряды или дифференциальные уравнения .

Из любого из этих определений можно показать, что e ^{− х} является обратной величиной e ^Икс . Например, из определения дифференциального уравнения e ^Икс Это ^{− х} = 1, когда x = 0 , а его производная по правилу произведения равна e ^Икс Это ^{− х} − и ^Икс Это ^{− х} = 0 для всех x , поэтому e ^Икс Это ^{− х} = 1 для всех x .

Из любого из этих определений можно показать, что показательная функция подчиняется основному тождеству возведения в степень . Например, из определения степенного ряда:

$$\exp(x+y)=\sum _{m=0}^{\infty }{\frac {(x+y)^{m}}{m!}}=\sum _{m=0}^{\infty }\sum _{k=0}^{m}{\frac {m!}{k!(m-k)!}}{\frac {x^{k}y^{m-k}}{m!}}=\sum _{n=0}^{\infty }\sum _{k=0}^{\infty }{\frac {x^{k}y^{n}}{k!n!}}=\exp x\cdot \exp y\,.$$

Это оправдывает обозначение e ^Икс для опыта х .

Производная ( скорость изменения) показательной функции является самой показательной функцией. В более общем смысле, функция со скоростью изменения, пропорциональной самой функции (а не равной ей), выражается через экспоненциальную функцию. Это свойство функции приводит к экспоненциальному росту или экспоненциальному затуханию .

Показательная функция расширяется до целой функции на комплексной плоскости . Формула Эйлера связывает свои значения при чисто мнимых аргументах с тригонометрическими функциями . Показательная функция также имеет аналоги, у которых аргументом является матрица или даже элемент банаховой алгебры или алгебры Ли .

Производные и дифференциальные уравнения

Производная показательной функции равна значению функции. Из любой точки P на кривой (синяя) проведем касательную (красную) и вертикальную линию (зеленую) высотой h , образующие прямоугольный треугольник с основанием b на оси x . Поскольку наклон красной касательной (производной) в точке P равен отношению высоты треугольника к основанию треугольника (подъём по разбегу), а производная равна значению функции, h должен быть равен отношение h к b . Следовательно, основание b всегда должно быть равно 1.

Важность показательной функции в математике и естественных науках проистекает главным образом из ее свойства как единственной функции, которая равна своей производной и равна 1 при x = 0 . То есть,

$${\frac {d}{dx}}e^{x}=e^{x}\quad {\text{and}}\quad e^{0}=1.$$

Функции формы ce ^Икс для константы c — единственные функции, равные своей производной (по теореме Пикара–Линделёфа ). Другие способы сказать то же самое включают в себя:

• Наклон графика в любой точке — это высота функции в этой точке.
• Скорость возрастания функции в точке x равна значению функции в точке x .
• Функция решает дифференциальное уравнение y ′ = y .
• exp — фиксированная точка производной как функционала .

Если скорость роста или распада переменной пропорциональна ее размеру — как в случае неограниченного роста населения (см. Мальтузианскую катастрофу ), непрерывно начисляемых процентов или радиоактивного распада — тогда переменную можно записать как константу, умноженную на экспоненциальную функцию времени. . Явно для любой действительной константы k функция f : R → R удовлетворяет условию f ′ = kf тогда и только тогда, когда f ( x ) = ce ^кх для некоторой постоянной c . Постоянная k называется константой распада , константой распада , константа скорости , или константа преобразования .

Кроме того, для любой дифференцируемой функции f находим по цепному правилу :

$${\frac {d}{dx}}e^{f(x)}=f'(x)e^{f(x)}.$$

Цепные дроби для e ^Икс

дробь Цепная для e ^Икс можно получить через тождество Эйлера :

$$e^{x}=1+{\cfrac {x}{1-{\cfrac {x}{x+2-{\cfrac {2x}{x+3-{\cfrac {3x}{x+4-\ddots }}}}}}}}$$

Следующая обобщенная цепная дробь для e ^С сходится быстрее:

$$e^{z}=1+{\cfrac {2z}{2-z+{\cfrac {z^{2}}{6+{\cfrac {z^{2}}{10+{\cfrac {z^{2}}{14+\ddots }}}}}}}}$$

или, применив замену z = х / у :

$$e^{\frac {x}{y}}=1+{\cfrac {2x}{2y-x+{\cfrac {x^{2}}{6y+{\cfrac {x^{2}}{10y+{\cfrac {x^{2}}{14y+\ddots }}}}}}}}$$

со специальным случаем для z = 2 :

$$e^{2}=1+{\cfrac {4}{0+{\cfrac {2^{2}}{6+{\cfrac {2^{2}}{10+{\cfrac {2^{2}}{14+\ddots \,}}}}}}}}=7+{\cfrac {2}{5+{\cfrac {1}{7+{\cfrac {1}{9+{\cfrac {1}{11+\ddots \,}}}}}}}}$$

Эта формула также сходится, хотя и медленнее, при z > 2 . Например:

$$e^{3}=1+{\cfrac {6}{-1+{\cfrac {3^{2}}{6+{\cfrac {3^{2}}{10+{\cfrac {3^{2}}{14+\ddots \,}}}}}}}}=13+{\cfrac {54}{7+{\cfrac {9}{14+{\cfrac {9}{18+{\cfrac {9}{22+\ddots \,}}}}}}}}$$

Сложная плоскость

Смотрите также: формула Эйлера § Определения комплексного возведения в степень

Показательная функция e^z, построенная на комплексной плоскости от -2-2i до 2+2i

Сложный сюжет , $z\mapsto \exp z$, с аргументом $\operatorname {Arg} \exp z$представлены различными оттенками. Переход от темных цветов к светлым показывает, что $\left|\exp z\right|$увеличивается только вправо. Периодические горизонтальные полосы, соответствующие одному и тому же оттенку, указывают на то, что $z\mapsto \exp z$ периодична ​ в части мнимой $z$.

Как и в реальном случае, показательная функция может быть определена на комплексной плоскости в нескольких эквивалентных формах.

Наиболее распространенное определение комплексной показательной функции аналогично определению степенного ряда для действительных аргументов, где действительная переменная заменяется комплексной:

$$\exp z:=\sum _{k=0}^{\infty }{\frac {z^{k}}{k!}}$$

Альтернативно, комплексная экспоненциальная функция может быть определена путем моделирования определения предела для реальных аргументов, но с заменой реальной переменной комплексной:

$$\exp z:=\lim _{n\to \infty }\left(1+{\frac {z}{n}}\right)^{n}$$

Что касается определения степенного ряда, почленное умножение двух копий этого степенного ряда в смысле Коши , разрешенное теоремой Мертенса , показывает, что определяющее мультипликативное свойство экспоненциальных функций продолжает сохраняться для всех комплексных аргументов:

$$\exp(w+z)=\exp w\exp z{\text{ for all }}w,z\in \mathbb {C}$$

Определение комплексной показательной функции, в свою очередь, приводит к соответствующим определениям, расширяющим тригонометрические функции на комплексные аргументы.

В частности, когда z = it ( treal ), определение ряда дает разложение

$$\exp(it)=\left(1-{\frac {t^{2}}{2!}}+{\frac {t^{4}}{4!}}-{\frac {t^{6}}{6!}}+\cdots \right)+i\left(t-{\frac {t^{3}}{3!}}+{\frac {t^{5}}{5!}}-{\frac {t^{7}}{7!}}+\cdots \right).$$

В этом разложении перестановка членов на действительную и мнимую части оправдана абсолютной сходимостью ряда. Действительная и мнимая части приведенного выше выражения фактически соответствуют разложению в ряды стоимости t и sin t соответственно.

Это соответствие дает мотивацию для определения косинуса и синуса для всех сложных аргументов в терминах $\exp(\pm iz)$ и эквивалентный степенной ряд:

$${\begin{aligned}&\cos z:={\frac {\exp(iz)+\exp(-iz)}{2}}=\sum _{k=0}^{\infty }(-1)^{k}{\frac {z^{2k}}{(2k)!}},\\[5pt]{\text{and }}\quad &\sin z:={\frac {\exp(iz)-\exp(-iz)}{2i}}=\sum _{k=0}^{\infty }(-1)^{k}{\frac {z^{2k+1}}{(2k+1)!}}\end{aligned}}$$

для всех ${\textstyle z\in \mathbb {C} .}$

Определенные таким образом функции exp , cos и sin имеют бесконечные радиусы сходимости по критерию отношения и, следовательно, являются целыми функциями (то есть голоморфными на $\mathbb {C}$). Диапазон экспоненциальной функции равен $\mathbb {C} \setminus \{0\}$, а диапазоны комплексных функций синуса и косинуса равны $\mathbb {C}$ в целом, в соответствии с теоремой Пикара , утверждающей, что область значений непостоянной целой функции равна либо всем из $\mathbb {C}$, или $\mathbb {C}$ исключая одно лакунарное значение .

Эти определения показательных и тригонометрических функций тривиально приводят к формуле Эйлера :

$$\exp(iz)=\cos z+i\sin z{\text{ for all }}z\in \mathbb {C} .$$

Альтернативно мы могли бы определить сложную показательную функцию, основанную на этом отношении. Если z = x + iy , где x и y действительны, то мы могли бы определить его экспоненту как

$$\exp z=\exp(x+iy):=(\exp x)(\cos y+i\sin y)$$

где exp , cos и sin в правой части знака определения следует интерпретировать как функции реальной переменной, ранее определенной другими способами.

Для $t\in \mathbb {R}$, отношение ${\overline {\exp(it)}}=\exp(-it)$ держится, так что $\left|\exp(it)\right|=1$ серьезно $t$ и $t\mapsto \exp(it)$отображает вещественную линию (mod 2 π ) в единичную окружность на комплексной плоскости. Более того, переходя от $t=0$ к $t=t_{0}$, кривая, определяемая $\gamma (t)=\exp(it)$ трассирует сегмент единичного круга длины

$$\int _{0}^{t_{0}}|\gamma '(t)|\,dt=\int _{0}^{t_{0}}|i\exp(it)|\,dt=t_{0},$$

начиная с z = 1 в комплексной плоскости и двигаясь против часовой стрелки. Основываясь на этих наблюдениях и на том факте, что мерой угла в радианах является длина дуги единичной окружности, опирающейся на угол, легко увидеть, что, если ограничиться действительными аргументами, функции синуса и косинуса, определенные выше, совпадают с функции синуса и косинуса, введенные в элементарную математику через геометрические понятия.

Комплексная показательная функция является периодической с периодом 2 πi и $\exp(z+2\pi ik)=\exp z$ держится для всех $z\in \mathbb {C} ,k\in \mathbb {Z}$.

При продолжении области определения от действительной прямой к комплексной плоскости показательная функция сохраняет следующие свойства:

$${\begin{aligned}&e^{z+w}=e^{z}e^{w}\,\\[5pt]&e^{0}=1\,\\[5pt]&e^{z}\neq 0\\[5pt]&{\frac {d}{dz}}e^{z}=e^{z}\\[5pt]&\left(e^{z}\right)^{n}=e^{nz},n\in \mathbb {Z} \end{aligned}}$$

для всех ${\textstyle w,z\in \mathbb {C} .}$

Расширение натурального логарифма до комплексных аргументов дает комплексный логарифм log z , который является многозначной функцией .

Затем мы можем определить более общее возведение в степень:

$$z^{w}=e^{w\log z}$$

для всех комплексных чисел z и w . Это также многозначная функция, даже если z действительно. Это различие проблематично, поскольку многозначные функции log z и z ^В их легко спутать со своими однозначными эквивалентами при замене z действительным числом . Правило умножения показателей степени для случая положительных действительных чисел должно быть изменено в многозначном контексте:

( Это ^С ) ^В
≠ и ^zw , а скорее ( е ^С ) ^В
= и ^{( z + 2 niπ ) ш} многозначный над целыми числами n

см . в разделе «Неисправность тождества степеней и логарифмов» Дополнительную информацию о проблемах с объединением степеней .

Экспоненциальная функция отображает любую линию на комплексной плоскости в логарифмическую спираль на комплексной плоскости с центром в начале координат . Существуют два особых случая: когда исходная линия параллельна действительной оси, результирующая спираль никогда не замыкается сама на себя; когда исходная линия параллельна воображаемой оси, результирующая спираль представляет собой круг некоторого радиуса.

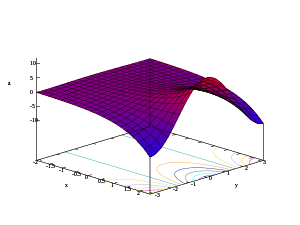
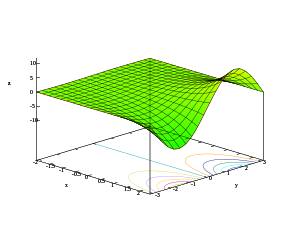
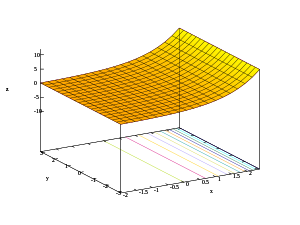
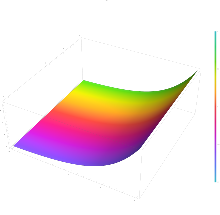
• Трехмерные графики действительной части, мнимой части и модуля показательной функции
• 
  z = Re( т.е. ^{х + яу} )
• 
  z = Im( е ^{х + яу} )
• 
  г = | Был ^{х + яу} |

Рассматривая комплексную показательную функцию как функцию четырех действительных переменных:

$$v+iw=\exp(x+iy)$$

график показательной функции представляет собой двумерную поверхность, изгибающуюся в четырех измерениях.

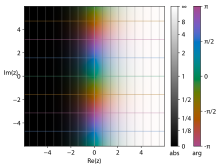
Начиная с цветной части $xy$ области ниже приведены изображения графа, проецированные в двух или трех измерениях.

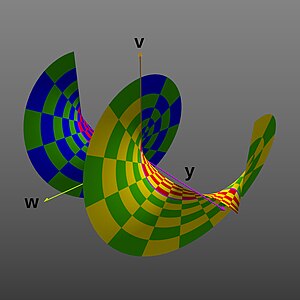
• Графики комплексной показательной функции
• 
  Ключ к шахматной доске:
  $x>0:\;{\text{green}}$
  $x<0:\;{\text{red}}$
  $y>0:\;{\text{yellow}}$
  $y<0:\;{\text{blue}}$
• 
  Проекция на комплексную плоскость дальности (V/W). Сравните со следующей перспективной картинкой.
• 
  Проекция в $x$, $v$, и $w$ размеры, создающие форму расширяющегося рога или воронки (представленную в виде двухмерного перспективного изображения)
• 
  Проекция в $y$, $v$, и $w$ размеры, создавая спиральную форму ( $y$ диапазон расширен до ±2 π , опять же как двумерное перспективное изображение)

На втором изображении показано, как комплексная плоскость домена отображается в комплексную плоскость диапазона:

• ноль отображается в 1
• реальность $x$ ось отображается на положительное действительное значение $v$ ось
• воображаемый $y$ ось вращается вокруг единичной окружности с постоянной угловой скоростью
• значения с отрицательными действительными частями отображаются внутри единичного круга
• значения с положительными действительными частями отображаются за пределами единичного круга
• значения с постоянной действительной частью отображаются в круги с центром в нуле
• значения с постоянной мнимой частью отображаются на лучи, идущие от нуля

Третье и четвертое изображения показывают, как график на втором изображении расширяется в одно из двух других измерений, не показанных на втором изображении.

На третьем изображении показан график, расширенный вдоль реальной $x$ось. Это показывает, что график представляет собой поверхность вращения относительно $x$ ось графика действительной показательной функции, образующей форму рога или воронки.

Четвертое изображение показывает график, расширенный вдоль воображаемой линии. $y$ось. Это показывает, что поверхность графика для положительных и отрицательных $y$ ценности на самом деле не совпадают с отрицательными реальными $v$ оси, а вместо этого образует спиральную поверхность вокруг $y$ось. Потому что это $y$ значения были расширены до ±2 π , это изображение также лучше отображает периодичность 2π в воображаемом $y$ ценить.

Расчет ​ ^б где и a , и b комплексные

Основная статья: Возведение в степень

Комплексное возведение в степень a ^б может быть определен путем преобразования a в полярные координаты и использования тождества ( e ^{в ​} ) ^б
= а ^б :

$$a^{b}=\left(re^{\theta i}\right)^{b}=\left(e^{(\ln r)+\theta i}\right)^{b}=e^{\left((\ln r)+\theta i\right)b}$$

Однако, когда b не является целым числом, эта функция является многозначной , поскольку θ не уникальна (см. Возведение в степень § Несостоятельность степенных и логарифмических тождеств ).

банаховы

Определение показательной функции степенным рядом имеет смысл для квадратных матриц (для которых функция называется матричной экспонентой в любой банаховой алгебре с единицей B. ) и, в более общем смысле , В этой обстановке э ⁰ = 1 и е ^Икс обратим с обратным e ^{− х} для любого x в B . Если xy = yx , то e ^{х + у} = и ^Икс Это ^и , но это тождество может оказаться неверным для некоммутирующих x и y .

Некоторые альтернативные определения приводят к той же функции. Например, э ^Икс может быть определен как

$$\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}.$$

Или е ^Икс можно определить как f _x (1) , где f _x : R → B — решение дифференциального уравнения df _x / dt ( t ) = x   f _x ( t ) , с начальным условием f _x (0) = 1 ; отсюда следует, что f _x ( t ) = e ^Техас для каждого t в R .

Алгебры Ли

Дана группа Ли G и связанная с ней алгебра Ли. ${\mathfrak {g}}$, экспоненциальное отображение - это отображение ${\mathfrak {g}}$ ↦ G , обладающая аналогичными свойствами. Фактически, поскольку R является алгеброй Ли группы Ли всех положительных действительных чисел при умножении, обычная показательная функция для вещественных аргументов является частным случаем ситуации алгебры Ли. Аналогично, поскольку группа Ли GL( n , R ) обратимых матриц размера n × n имеет в качестве алгебры Ли M( n , R ) пространство всех матриц размера n × n , показательная функция для квадратных матриц является частным случаем Экспоненциальное отображение алгебры Ли.

Личность $\exp(x+y)=\exp(x)\exp(y)$может потерпеть неудачу для элементов алгебры Ли x и y , которые не коммутируют; формула Бейкера -Кэмпбелла-Хаусдорфа дает необходимые корректирующие члены.

Трансцендентность

Функция е ^С не находится в кольце рациональных функций $\mathbb {C} (z)$: это не частное двух многочленов с комплексными коэффициентами.

Если a ₁ , ..., an _— различные комплексные числа, то e ^{а ₁ з} , ..., Это ^{а _н з} линейно независимы относительно $\mathbb {C} (z)$, и, следовательно, e ^С является трансцендентным по отношению к $\mathbb {C} (z)$.

Вычисление

При вычислении (аппроксимации) показательной функции вблизи аргумента 0 результат будет близок к 1, а вычисление значения разности $e^{x}-1$ с арифметикой с плавающей запятой может привести к потере (возможно, всех) значащих цифр , что приведет к большой ошибке расчета и, возможно, даже к бессмысленному результату.

По предложению Уильяма Кахана , возможно, было бы полезно иметь специальный распорядок дня, часто называемый expm1, для вычисления e ^Икс − 1 напрямую, минуя вычисление e ^Икс . Например, если экспонента вычисляется с использованием ряда Тейлора

$$e^{x}=1+x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+\cdots +{\frac {x^{n}}{n!}}+\cdots ,$$

можно использовать ряд Тейлора $e^{x}-1$:

$$e^{x}-1=x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+\cdots +{\frac {x^{n}}{n!}}+\cdots .$$

Впервые это было реализовано в 1979 году в калькуляторе Hewlett-Packard HP-41C и реализовано в нескольких калькуляторах. операционные системы (например, Berkeley UNIX 4.3BSD ), системы компьютерной алгебры и языки программирования (например, C99 ).

В дополнение к основанию e стандарт IEEE 754-2008 определяет аналогичные показательные функции вблизи 0 для оснований 2 и 10: $2^{x}-1$ и $10^{x}-1$.

Аналогичный подход использовался для логарифма (см. lnp1 ).

Тождество в терминах гиперболического тангенса ,

$$\operatorname {expm1} (x)=e^{x}-1={\frac {2\tanh(x/2)}{1-\tanh(x/2)}},$$

дает значение высокой точности для небольших значений x в системах, которые не реализуют expm1( x ) .

См. также

• Экспонента Карлица , характеристический p аналог
• Двойная показательная функция - Показательная функция показательной функции.
• Экспоненциальное поле – математическое поле с дополнительной операцией.
• Функция Гаусса
• Полуэкспоненциальная функция , композиционный квадратный корень показательной функции.
• Lambert_W_function#Solving_equations – Многозначная функция в математике. Используется для решения показательных уравнений.
• Список экспоненциальных тем
• Список интегралов показательных функций
• Функция Миттаг-Леффлера , обобщение показательной функции
• p -адическая показательная функция
• Таблица Паде для показательной функции - аппроксимация Паде показательной функции дробью полиномиальной функции
• Фазовый коэффициент

Внешние ссылки

• «Показательная функция» , Математическая энциклопедия , EMS Press , 2001 [1994]