Интеграция по частям

В исчислении и, в более общем плане, в анализе , интегрирование по частям или частичное интегрирование — это процесс, который находит интеграл от произведения функций математическом через интеграл от произведения их производной и первообразной . Его часто используют для преобразования первообразной произведения функций в первообразную, для которой легче найти решение. Это правило можно рассматривать как интегральную версию продукта дифференциации правила ; оно действительно получено с использованием правила произведения.

Формула интегрирования по частям гласит:

$${\begin{aligned}\int _{a}^{b}u(x)v'(x)\,dx&={\Big [}u(x)v(x){\Big ]}_{a}^{b}-\int _{a}^{b}u'(x)v(x)\,dx\\&=u(b)v(b)-u(a)v(a)-\int _{a}^{b}u'(x)v(x)\,dx.\end{aligned}}$$

Или, позволив $u=u(x)$ и $du=u'(x)\,dx$ пока $v=v(x)$ и $dv=v'(x)\,dx,$ формулу можно записать более компактно:

$$\int u\,dv\ =\ uv-\int v\,du.$$

Важно отметить, что первое выражение записывается в виде определенного интеграла, а второе — в виде неопределенного интеграла. Применение соответствующих ограничений к последнему выражению должно привести к первому, но последнее не обязательно эквивалентно первому.

Математик Брук Тейлор открыл интегрирование по частям, впервые опубликовав эту идею в 1715 году. Более общие формулировки интегрирования по частям существуют для интегралов Римана–Стилтьеса и Лебега–Стилтьеса . Дискретный . аналог последовательностей называется по частям суммированием

Теорема

Произведение двух функций

Теорему можно вывести следующим образом. Для двух непрерывно дифференцируемых функций $u(x)$ и $v(x)$правило продукта гласит:

$${\Big (}u(x)v(x){\Big )}'=v(x)u'(x)+u(x)v'(x).$$

Интеграция обеих сторон в отношении $x$,

$$\int {\Big (}u(x)v(x){\Big )}'\,dx=\int u'(x)v(x)\,dx+\int u(x)v'(x)\,dx,$$

и учитывая, что неопределенный интеграл является первообразной, дает

$$u(x)v(x)=\int u'(x)v(x)\,dx+\int u(x)v'(x)\,dx,$$

где мы пренебрегаем записью константы интегрирования . В результате получается формула интегрирования по частям :

$$\int u(x)v'(x)\,dx=u(x)v(x)-\int u'(x)v(x)\,dx,$$

или в терминах дифференциалов $du=u'(x)\,dx$, $dv=v'(x)\,dx,\quad$

$$\int u(x)\,dv=u(x)v(x)-\int v(x)\,du.$$

Под этим следует понимать равенство функций с добавлением к каждой стороне неопределенной константы. Взяв разницу каждой стороны между двумя значениями $x=a$ и $x=b$ и применение фундаментальной теоремы исчисления дает определенную интегральную версию:

$$\int _{a}^{b}u(x)v'(x)\,dx=u(b)v(b)-u(a)v(a)-\int _{a}^{b}u'(x)v(x)\,dx.$$

Исходный интеграл $\int uv'\,dx$ содержит производную v' ; Чтобы применить теорему, нужно найти v , первообразную v ' , а затем вычислить полученный интеграл $\int vu'\,dx.$

Применимость для менее гладких функций

Это не обязательно для $u$ и $v$ быть непрерывно дифференцируемым. Интегрирование по частям работает, если $u$ абсолютно непрерывна и функция, обозначенная $v'$ интегрируема по Лебегу (но не обязательно непрерывна). (Если $v'$ имеет точку разрыва, то ее первообразная $v$ в этой точке может не быть производной.)

Если интервал интегрирования не компактен , то в этом нет необходимости. $u$ быть абсолютно непрерывным на всем интервале или для $v'$ быть интегрируемым по Лебегу на интервале, как пара примеров (в которых $u$ и $v$ непрерывны и непрерывно дифференцируемы) покажет. Например, если

$$u(x)=e^{x}/x^{2},\,v'(x)=e^{-x}$$

$u$ не является абсолютно непрерывным на интервале [1, ∞) , но тем не менее

$$\int _{1}^{\infty }u(x)v'(x)\,dx={\Big [}u(x)v(x){\Big ]}_{1}^{\infty }-\int _{1}^{\infty }u'(x)v(x)\,dx$$

до тех пор, пока $\left[u(x)v(x)\right]_{1}^{\infty }$ понимается как предел $u(L)v(L)-u(1)v(1)$ как $L\to \infty$ и пока два члена в правой части конечны. Это верно только в том случае, если мы выбираем $v(x)=-e^{-x}.$ Аналогично, если

$$u(x)=e^{-x},\,v'(x)=x^{-1}\sin(x)$$

$v'$ не интегрируемо по Лебегу на интервале [1, ∞) , но тем не менее

$$\int _{1}^{\infty }u(x)v'(x)\,dx={\Big [}u(x)v(x){\Big ]}_{1}^{\infty }-\int _{1}^{\infty }u'(x)v(x)\,dx$$

с той же интерпретацией.

Можно также легко привести подобные примеры, в которых $u$ и $v$ являются не непрерывно дифференцируемыми.

Далее, если $f(x)$ есть функция ограниченной вариации на отрезке $[a,b],$ и $\varphi (x)$ дифференцируема по $[a,b],$ затем

$$\int _{a}^{b}f(x)\varphi '(x)\,dx=-\int _{-\infty }^{\infty }{\widetilde {\varphi }}(x)\,d({\widetilde {\chi }}_{[a,b]}(x){\widetilde {f}}(x)),$$

где $d(\chi _{[a,b]}(x){\widetilde {f}}(x))$ обозначает знаковую меру, соответствующую функции ограниченной вариации $\chi _{[a,b]}(x)f(x)$и функции ${\widetilde {f}},{\widetilde {\varphi }}$ являются продолжением $f,\varphi$ к $\mathbb {R} ,$ которые соответственно имеют ограниченную вариацию и дифференцируемы.

Многофункциональный продукт

Интегрирование правила произведения для трех умноженных функций, $u(x)$, $v(x)$, $w(x)$, дает аналогичный результат:

$$\int _{a}^{b}uv\,dw\ =\ {\Big [}uvw{\Big ]}_{a}^{b}-\int _{a}^{b}uw\,dv-\int _{a}^{b}vw\,du.$$

В общем, для $n$ факторы

$$\left(\prod _{i=1}^{n}u_{i}(x)\right)'\ =\ \sum _{j=1}^{n}u_{j}'(x)\prod _{i\neq j}^{n}u_{i}(x),$$

что приводит к

$$\left[\prod _{i=1}^{n}u_{i}(x)\right]_{a}^{b}\ =\ \sum _{j=1}^{n}\int _{a}^{b}u_{j}'(x)\prod _{i\neq j}^{n}u_{i}(x).$$

Визуализация

Графическая интерпретация теоремы. Изображенная кривая параметризована переменной t.

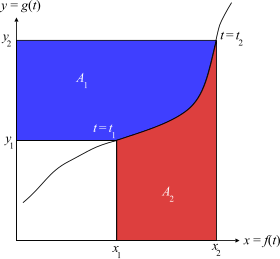
Рассмотрим параметрическую кривую по формуле ( x , y ) = ( f ( t ), g ( t )). Предполагая, что кривая локально однозначно и интегрируема , мы можем определить

$${\begin{aligned}x(y)&=f(g^{-1}(y))\\y(x)&=g(f^{-1}(x))\end{aligned}}$$

Площадь синей области равна

$$A_{1}=\int _{y_{1}}^{y_{2}}x(y)\,dy$$

Аналогично, площадь красной области равна

$$A_{2}=\int _{x_{1}}^{x_{2}}y(x)\,dx$$

Общая площадь A ₁ + A ₂ равна площади большего прямоугольника x ₂ y ₂ минус площадь меньшего x ₁ y ₁ :

$$\overbrace {\int _{y_{1}}^{y_{2}}x(y)\,dy} ^{A_{1}}+\overbrace {\int _{x_{1}}^{x_{2}}y(x)\,dx} ^{A_{2}}\ =\ {\biggl .}x\cdot y(x){\biggl |}_{x_{1}}^{x_{2}}\ =\ {\biggl .}y\cdot x(y){\biggl |}_{y_{1}}^{y_{2}}$$

Или, с точки зрения t ,

$$\int _{t_{1}}^{t_{2}}x(t)\,dy(t)+\int _{t_{1}}^{t_{2}}y(t)\,dx(t)\ =\ {\biggl .}x(t)y(t){\biggl |}_{t_{1}}^{t_{2}}$$

Или, в терминах неопределенных интегралов, это можно записать как

$$\int x\,dy+\int y\,dx\ =\ xy$$

Перестановка:

$$\int x\,dy\ =\ xy-\int y\,dx$$

Таким образом, интегрирование по частям можно рассматривать как выведение площади синей области из площади прямоугольников и площади красной области.

Эта визуализация также объясняет, почему интегрирование по частям может помочь найти интеграл обратной функции f. ⁻¹ ( x интеграл функции f ( x ), когда известен ). Действительно, функции x ( y ) и y ( x ) являются обратными, и интеграл ∫ x   dy можно вычислить, как указано выше, зная интеграл ∫ y   dx . В частности, этим объясняется использование интегрирования по частям для интегрирования логарифмов и обратных тригонометрических функций . Фактически, если $f$ является дифференцируемой взаимно однозначной функцией на интервале, то интегрирование по частям можно использовать для вывода формулы для интеграла от $f^{-1}$с точки зрения интеграла $f$. Это продемонстрировано в статье Интеграл от обратных функций .

Приложения

Нахождение первообразных

Интегрирование по частям — это эвристический , а не чисто механический процесс решения интегралов; учитывая одну функцию для интегрирования, типичная стратегия состоит в том, чтобы тщательно разделить эту единственную функцию на произведение двух функций u ( x ) v ( x ) так, чтобы остаточный интеграл от формулы интегрирования по частям легче вычислить, чем одну функцию . Следующая форма полезна для иллюстрации наилучшей стратегии:

$$\int uv\,dx=u\int v\,dx-\int \left(u'\int v\,dx\right)\,dx.$$

В правой части u дифференцируется, а v интегрируется; следовательно, полезно выбрать u как функцию, которая упрощается при дифференцировании, или выбрать v как функцию, которая упрощается при интегрировании. В качестве простого примера рассмотрим:

$$\int {\frac {\ln(x)}{x^{2}}}\,dx\,.$$

Поскольку производная ln( x ) равна 1 / x , делается (ln( x )) частью u ; поскольку первообразная 1 / х ² это — 1 / x , получается 1 / х ² часть v . Теперь формула дает:

$$\int {\frac {\ln(x)}{x^{2}}}\,dx=-{\frac {\ln(x)}{x}}-\int {\biggl (}{\frac {1}{x}}{\biggr )}{\biggl (}-{\frac {1}{x}}{\biggr )}\,dx\,.$$

Первообразная — 1 / х ² можно найти с помощью степенного правила и 1 / х .

В качестве альтернативы можно выбрать u и v так, чтобы произведение u ′ (∫ v   dx ) упростилось из-за сокращения. Например, предположим, что кто-то хочет интегрировать:

$$\int \sec ^{2}(x)\cdot \ln {\Big (}{\bigl |}\sin(x){\bigr |}{\Big )}\,dx.$$

Если мы выберем u ( x ) = ln(|sin( x )|) и v ( x ) = sec ² x, затем u дифференцируется до 1/ tan x с использованием цепного правила , а v интегрируется до tan x ; поэтому формула дает:

$$\int \sec ^{2}(x)\cdot \ln {\Big (}{\bigl |}\sin(x){\bigr |}{\Big )}\,dx=\tan(x)\cdot \ln {\Big (}{\bigl |}\sin(x){\bigr |}{\Big )}-\int \tan(x)\cdot {\frac {1}{\tan(x)}}\,dx\ .$$

Подынтегральная функция упрощается до 1, поэтому первообразная равна x . Поиск упрощающей комбинации часто требует экспериментирования.

В некоторых приложениях может не потребоваться гарантировать, что интеграл, полученный путем интегрирования по частям, имеет простую форму; например, при численном анализе может быть достаточно, чтобы он имел небольшую величину и поэтому вносил лишь небольшой погрешность. Некоторые другие специальные методы продемонстрированы в примерах ниже.

Полиномы и тригонометрические функции

Чтобы вычислить

$$I=\int x\cos(x)\,dx\,,$$

позволять:

$${\begin{alignedat}{3}u&=x\ &\Rightarrow \ &&du&=dx\\dv&=\cos(x)\,dx\ &\Rightarrow \ &&v&=\int \cos(x)\,dx=\sin(x)\end{alignedat}}$$

затем:

$${\begin{aligned}\int x\cos(x)\,dx&=\int u\ dv\\&=u\cdot v-\int v\,du\\&=x\sin(x)-\int \sin(x)\,dx\\&=x\sin(x)+\cos(x)+C,\end{aligned}}$$

где C — константа интегрирования .

Для высших сил $x$ в форме

$$\int x^{n}e^{x}\,dx,\ \int x^{n}\sin(x)\,dx,\ \int x^{n}\cos(x)\,dx\,,$$

повторное использование интегрирования по частям позволяет вычислить такие интегралы; каждое применение теоремы снижает мощность $x$ по одному.

Экспоненты и тригонометрические функции

См. Также: Интегрирование по формуле Эйлера.

Примером, обычно используемым для изучения работы интегрирования по частям, является

$$I=\int e^{x}\cos(x)\,dx.$$

Здесь интегрирование по частям производится дважды. Сначала позвольте

$${\begin{alignedat}{3}u&=\cos(x)\ &\Rightarrow \ &&du&=-\sin(x)\,dx\\dv&=e^{x}\,dx\ &\Rightarrow \ &&v&=\int e^{x}\,dx=e^{x}\end{alignedat}}$$

затем:

$$\int e^{x}\cos(x)\,dx=e^{x}\cos(x)+\int e^{x}\sin(x)\,dx.$$

Теперь, чтобы вычислить оставшийся интеграл, мы снова используем интегрирование по частям:

$${\begin{alignedat}{3}u&=\sin(x)\ &\Rightarrow \ &&du&=\cos(x)\,dx\\dv&=e^{x}\,dx\,&\Rightarrow \ &&v&=\int e^{x}\,dx=e^{x}.\end{alignedat}}$$

Затем:

$$\int e^{x}\sin(x)\,dx=e^{x}\sin(x)-\int e^{x}\cos(x)\,dx.$$

Соединив это вместе,

$$\int e^{x}\cos(x)\,dx=e^{x}\cos(x)+e^{x}\sin(x)-\int e^{x}\cos(x)\,dx.$$

Один и тот же интеграл появляется в обеих частях этого уравнения. Интеграл можно просто сложить с обеих частей, чтобы получить

$$2\int e^{x}\cos(x)\,dx=e^{x}{\bigl [}\sin(x)+\cos(x){\bigr ]}+C,$$

который перестраивается в

$$\int e^{x}\cos(x)\,dx={\frac {1}{2}}e^{x}{\bigl [}\sin(x)+\cos(x){\bigr ]}+C'$$

где снова $C$ (и $C'=C/2$) — константа интегрирования .

Аналогичный метод используется для нахождения интеграла от секущего в кубе .

Функции, умноженные на единицу

Два других хорошо известных примера — это когда интегрирование по частям применяется к функции, выраженной как произведение 1 и самой себя. Это работает, если известна производная функции, а интеграл от этой производной умножен на $x$ также известно.

Первый пример $\int \ln(x)dx$. Мы пишем это как:

$$I=\int \ln(x)\cdot 1\,dx\,.$$

Позволять:

$$u=\ln(x)\ \Rightarrow \ du={\frac {dx}{x}}$$

$$dv=dx\ \Rightarrow \ v=x$$

затем:

$${\begin{aligned}\int \ln(x)\,dx&=x\ln(x)-\int {\frac {x}{x}}\,dx\\&=x\ln(x)-\int 1\,dx\\&=x\ln(x)-x+C\end{aligned}}$$

где $C$ – константа интегрирования .

Второй пример — обратного тангенса. функция $\arctan(x)$:

$$I=\int \arctan(x)\,dx.$$

Перепишите это как

$$\int \arctan(x)\cdot 1\,dx.$$

Теперь позвольте:

$$u=\arctan(x)\ \Rightarrow \ du={\frac {dx}{1+x^{2}}}$$

$$dv=dx\ \Rightarrow \ v=x$$

затем

$${\begin{aligned}\int \arctan(x)\,dx&=x\arctan(x)-\int {\frac {x}{1+x^{2}}}\,dx\\[8pt]&=x\arctan(x)-{\frac {\ln(1+x^{2})}{2}}+C\end{aligned}}$$

используя комбинацию метода правила обратной цепи и условия интеграла натурального логарифма .

Правило LIATE

Правило LIATE — это практическое правило объединения по частям. Он предполагает выбор в качестве функции , которая стоит первой в следующем списке:

• L – логарифмические функции : $\ln(x),\ \log _{b}(x),$ и т. д.
• I – обратные тригонометрические функции (включая гиперболические аналоги ): $\arctan(x),\ \operatorname {arcsec}(x),\ \operatorname {arsinh} (x),$ и т. д.
• А – алгебраические функции (например, многочлены ): $x^{2},\ 3x^{50},$ и т. д.
• Т – тригонометрические функции (включая гиперболические аналоги ): $\sin(x),\ \tan(x),\ \operatorname {sech} (x),$ и т. д.
• E – показательные функции : $e^{x},\ 19^{x},$ и т. д.

Функция, которая будет называться dv, будет той, которая стоит последней в списке. Причина в том, что функции, расположенные ниже в списке, обычно имеют более простые первообразные, чем функции, расположенные выше. Правило иногда записывается как «ДЕТАЛЬ», где D означает dv , а верхняя часть списка — это функция, выбранная в качестве dv . Альтернативой этому правилу является правило ILATE, согласно которому обратные тригонометрические функции предшествуют логарифмическим функциям.

Чтобы продемонстрировать правило LIATE, рассмотрим интеграл

$$\int x\cdot \cos(x)\,dx.$$

Следуя правилу LIATE, u = x и dv = cos( x ) dx , следовательно, du = dx и v = sin( x ), что приводит к тому, что интеграл становится

$$x\cdot \sin(x)-\int 1\sin(x)\,dx,$$

что равно

$$x\cdot \sin(x)+\cos(x)+C.$$

Обычно стараются выбрать u и dv так, чтобы du было проще, чем u , а dv легко интегрировать. Если бы вместо этого cos( x ) было выбрано как u , а x dx как dv , мы бы имели интеграл

$${\frac {x^{2}}{2}}\cos(x)+\int {\frac {x^{2}}{2}}\sin(x)\,dx,$$

что после рекурсивного применения формулы интегрирования по частям явно привело бы к бесконечной рекурсии и ни к чему не привело.

Хотя это полезное эмпирическое правило, из правила LIATE есть исключения. Распространенной альтернативой является рассмотрение правил в порядке «ILATE». Кроме того, в некоторых случаях полиномиальные члены необходимо разбивать нетривиальными способами. Например, интегрировать

$$\int x^{3}e^{x^{2}}\,dx,$$

можно было бы установить

$$u=x^{2},\quad dv=x\cdot e^{x^{2}}\,dx,$$

так что

$$du=2x\,dx,\quad v={\frac {e^{x^{2}}}{2}}.$$

Затем

$$\int x^{3}e^{x^{2}}\,dx=\int \left(x^{2}\right)\left(xe^{x^{2}}\right)\,dx=\int u\,dv=uv-\int v\,du={\frac {x^{2}e^{x^{2}}}{2}}-\int xe^{x^{2}}\,dx.$$

Наконец, это приводит к

$$\int x^{3}e^{x^{2}}\,dx={\frac {e^{x^{2}}\left(x^{2}-1\right)}{2}}+C.$$

Интегрирование по частям часто используется как инструмент доказательства теорем математического анализа .

Продукт Уоллиса

Бесконечное произведение Уоллиса для $\pi$

$${\begin{aligned}{\frac {\pi }{2}}&=\prod _{n=1}^{\infty }{\frac {4n^{2}}{4n^{2}-1}}=\prod _{n=1}^{\infty }\left({\frac {2n}{2n-1}}\cdot {\frac {2n}{2n+1}}\right)\\[6pt]&={\Big (}{\frac {2}{1}}\cdot {\frac {2}{3}}{\Big )}\cdot {\Big (}{\frac {4}{3}}\cdot {\frac {4}{5}}{\Big )}\cdot {\Big (}{\frac {6}{5}}\cdot {\frac {6}{7}}{\Big )}\cdot {\Big (}{\frac {8}{7}}\cdot {\frac {8}{9}}{\Big )}\cdot \;\cdots \end{aligned}}$$

можно получить с помощью интегрирования по частям .

Идентичность гамма-функции

Гамма -функция является примером специальной функции , определяемой как несобственный интеграл для $z>0$. Интегрирование по частям показывает, что оно является расширением функции факториала:

$${\begin{aligned}\Gamma (z)&=\int _{0}^{\infty }e^{-x}x^{z-1}dx\\[6pt]&=-\int _{0}^{\infty }x^{z-1}\,d\left(e^{-x}\right)\\[6pt]&=-{\Biggl [}e^{-x}x^{z-1}{\Biggl ]}_{0}^{\infty }+\int _{0}^{\infty }e^{-x}d\left(x^{z-1}\right)\\[6pt]&=0+\int _{0}^{\infty }\left(z-1\right)x^{z-2}e^{-x}dx\\[6pt]&=(z-1)\Gamma (z-1).\end{aligned}}$$

С

$$\Gamma (1)=\int _{0}^{\infty }e^{-x}\,dx=1,$$

когда $z$ является натуральным числом, то есть $z=n\in \mathbb {N}$многократное применение этой формулы дает факториал : $\Gamma (n+1)=n!$

в

Интегрирование по частям часто используется в гармоническом анализе , особенно в анализе Фурье , чтобы показать, что быстро осциллирующие интегралы с достаточно гладкими подынтегральными выражениями быстро затухают . Наиболее распространенным примером этого является его использование для демонстрации того, что затухание преобразования Фурье функции зависит от гладкости этой функции, как описано ниже.

производной

Если $f$ это $k$-раз непрерывно дифференцируемая функция и все производные с точностью до $k$если один распадается до нуля на бесконечности, то его преобразование Фурье удовлетворяет условию

$$({\mathcal {F}}f^{(k)})(\xi )=(2\pi i\xi )^{k}{\mathcal {F}}f(\xi ),$$

где $f^{(k)}$ это $k$-я производная от $f$. (Точная константа справа зависит от соглашения о используемом преобразовании Фурье .) Это доказывается, если отметить, что

$${\frac {d}{dy}}e^{-2\pi iy\xi }=-2\pi i\xi e^{-2\pi iy\xi },$$

поэтому, используя интегрирование по частям преобразования Фурье производной, мы получаем

$${\begin{aligned}({\mathcal {F}}f')(\xi )&=\int _{-\infty }^{\infty }e^{-2\pi iy\xi }f'(y)\,dy\\&=\left[e^{-2\pi iy\xi }f(y)\right]_{-\infty }^{\infty }-\int _{-\infty }^{\infty }(-2\pi i\xi e^{-2\pi iy\xi })f(y)\,dy\\[5pt]&=2\pi i\xi \int _{-\infty }^{\infty }e^{-2\pi iy\xi }f(y)\,dy\\[5pt]&=2\pi i\xi {\mathcal {F}}f(\xi ).\end{aligned}}$$

Применение этого индуктивного метода дает результат для общего $k$. Аналогичный метод можно использовать для нахождения преобразования Лапласа производной функции.

Распад

Приведенный выше результат говорит нам о затухании преобразования Фурье, поскольку из него следует, что если $f$ и $f^{(k)}$ интегрируемы, то

$$\vert {\mathcal {F}}f(\xi )\vert \leq {\frac {I(f)}{1+\vert 2\pi \xi \vert ^{k}}},{\text{ where }}I(f)=\int _{-\infty }^{\infty }{\Bigl (}\vert f(y)\vert +\vert f^{(k)}(y)\vert {\Bigr )}\,dy.$$

Другими словами, если $f$ удовлетворяет этим условиям, то его преобразование Фурье затухает на бесконечности по крайней мере так же быстро, как 1/| ξ | ^к . В частности, если $k\geq 2$ тогда преобразование Фурье интегрируемо.

В доказательстве используется тот факт, который непосредственно следует из определения преобразования Фурье , что

$$\vert {\mathcal {F}}f(\xi )\vert \leq \int _{-\infty }^{\infty }\vert f(y)\vert \,dy.$$

Использование той же идеи о равенстве, изложенной в начале этого подраздела, дает

$$\vert (2\pi i\xi )^{k}{\mathcal {F}}f(\xi )\vert \leq \int _{-\infty }^{\infty }\vert f^{(k)}(y)\vert \,dy.$$

Суммируя эти два неравенства и затем деля на 1 + |2 π ξ ^к | дает указанное неравенство.

в

Одно из применений интегрирования по частям в теории операторов состоит в том, что оно показывает, что −∆ (где ∆ — оператор Лапласа ) является положительным оператором на $L^{2}$ (см . Л ^п космос ). Если $f$ является гладким и компактно поддерживаемым, то, используя интегрирование по частям, имеем

$${\begin{aligned}\langle -\Delta f,f\rangle _{L^{2}}&=-\int _{-\infty }^{\infty }f''(x){\overline {f(x)}}\,dx\\[5pt]&=-\left[f'(x){\overline {f(x)}}\right]_{-\infty }^{\infty }+\int _{-\infty }^{\infty }f'(x){\overline {f'(x)}}\,dx\\[5pt]&=\int _{-\infty }^{\infty }\vert f'(x)\vert ^{2}\,dx\geq 0.\end{aligned}}$$

Другие приложения

• Определение граничных условий в теории Штурма–Лиувилля
• Вывод уравнения Эйлера–Лагранжа в вариационном исчислении

Повторное интегрирование по частям

Учитывая вторую производную от $v$ в интеграле по левой части формулы частичного интегрирования предполагает повторное применение к интегралу по правой части:

$$\int uv''\,dx=uv'-\int u'v'\,dx=uv'-\left(u'v-\int u''v\,dx\right).$$

Распространение этой концепции повторного частичного интегрирования на производные степени n приводит к

$${\begin{aligned}\int u^{(0)}v^{(n)}\,dx&=u^{(0)}v^{(n-1)}-u^{(1)}v^{(n-2)}+u^{(2)}v^{(n-3)}-\cdots +(-1)^{n-1}u^{(n-1)}v^{(0)}+(-1)^{n}\int u^{(n)}v^{(0)}\,dx.\\[5pt]&=\sum _{k=0}^{n-1}(-1)^{k}u^{(k)}v^{(n-1-k)}+(-1)^{n}\int u^{(n)}v^{(0)}\,dx.\end{aligned}}$$

Эта концепция может быть полезна, когда последовательные интегралы $v^{(n)}$ легко доступны (например, простые экспоненты или синус и косинус, как в преобразованиях Лапласа или Фурье ), и когда n -я производная $u$ обращается в нуль (например, как полиномиальная функция степени $(n-1)$). Последнее условие останавливает повторение частичного интегрирования, поскольку правый интеграл исчезает.

В ходе описанного выше повторения частичных интегрирований интегралы

$$\int u^{(0)}v^{(n)}\,dx\quad$$

и $\quad \int u^{(\ell )}v^{(n-\ell )}\,dx\quad$ и $\quad \int u^{(m)}v^{(n-m)}\,dx\quad {\text{ for }}1\leq m,\ell \leq n$родниться. Это можно интерпретировать как произвольное «перемещение» деривативов между $v$ и $u$ внутри подынтегральной функции и тоже оказывается полезным (см. формулу Родригеса ).

Табличное интегрирование по частям

Основной процесс приведенной выше формулы можно резюмировать в таблице; полученный метод называется «табличным интегрированием» и был показан в фильме «Выстоять и доставить» (1988).

Например, рассмотрим интеграл

$$\int x^{3}\cos x\,dx\quad$$

и возьми $\quad u^{(0)}=x^{3},\quad v^{(n)}=\cos x.$

Начните перечислять в столбце А функцию $u^{(0)}=x^{3}$ и его последующие производные $u^{(i)}$ пока не будет достигнут ноль. Затем перечислите в столбце B функцию $v^{(n)}=\cos x$ и его последующие интегралы $v^{(n-i)}$ пока размер столбца B не станет таким же, как размер столбца A. до тех пор , Результат следующий:

# я	Знак	А: производные $u^{(i)}$	Б: интегралы $v^{(n-i)}$
0	+	$x^{3}$	$\cos x$
1	−	$3x^{2}$	$\sin x$
2	+	$6x$	$-\cos x$
3	−	$6$	$-\sin x$
4	+	$0$	$\cos x$

Произведение записей в строке i столбцов A и B вместе с соответствующим знаком дает соответствующие интегралы на шаге i в ходе повторного интегрирования по частям. Шаг i = 0 дает исходный интеграл. Для получения полного результата на шаге i > 0 должен i -й интеграл быть добавлен ко всем предыдущим произведениям ( 0 ≤ j < i ) j -й записи столбца A и ( j + 1) -й записи столбца B (т. е. , умножьте 1-ю запись столбца A на 2-ю запись столбца B, 2-ю запись столбца A на 3-ю запись столбца B и т. д. ...) с заданным j -м знаком. Этот процесс естественным образом останавливается, когда произведение, дающее интеграл, становится равным нулю ( i = 4 в примере ). Полный результат следующий (с чередующимися знаками в каждом члене):

$$\underbrace {(+1)(x^{3})(\sin x)} _{j=0}+\underbrace {(-1)(3x^{2})(-\cos x)} _{j=1}+\underbrace {(+1)(6x)(-\sin x)} _{j=2}+\underbrace {(-1)(6)(\cos x)} _{j=3}+\underbrace {\int (+1)(0)(\cos x)\,dx} _{i=4:\;\to \;C}.$$

Это дает

$$\underbrace {\int x^{3}\cos x\,dx} _{\text{step 0}}=x^{3}\sin x+3x^{2}\cos x-6x\sin x-6\cos x+C.$$

Повторное частичное интегрирование оказывается полезным и тогда, когда в ходе соответственно дифференцирования и интегрирования функций $u^{(i)}$ и $v^{(n-i)}$ их произведение дает кратное исходному подынтегральному выражении. В этом случае повторение также может быть прекращено с помощью этого индекса i. Ожидается, что это может произойти с экспонентами и тригонометрическими функциями. В качестве примера рассмотрим

$$\int e^{x}\cos x\,dx.$$

# я	Знак	А: производные $u^{(i)}$	Б: интегралы $v^{(n-i)}$
0	+	$e^{x}$	$\cos x$
1	−	$e^{x}$	$\sin x$
2	+	$e^{x}$	$-\cos x$

В этом случае произведение членов в столбцах A и B с соответствующим знаком для индекса i = 2 дает отрицательный результат исходного подынтегрального выражения (сравните строки i = 0 и i = 2 ).

$$\underbrace {\int e^{x}\cos x\,dx} _{\text{step 0}}=\underbrace {(+1)(e^{x})(\sin x)} _{j=0}+\underbrace {(-1)(e^{x})(-\cos x)} _{j=1}+\underbrace {\int (+1)(e^{x})(-\cos x)\,dx} _{i=2}.$$

Заметив, что интеграл в правой части может иметь собственную константу интегрирования. $C'$и перенос абстрактного интеграла в другую сторону дает

$$2\int e^{x}\cos x\,dx=e^{x}\sin x+e^{x}\cos x+C',$$

и наконец:

$$\int e^{x}\cos x\,dx={\frac {1}{2}}\left(e^{x}(\sin x+\cos x)\right)+C,$$

где $C=C'/2$.

Высшие измерения

Интегрирование по частям можно распространить на функции нескольких переменных, применив версию фундаментальной теоремы исчисления к соответствующему правилу произведения. В многомерном исчислении возможно несколько таких пар, включающих скалярную функцию u и векторную функцию (векторное поле) V .

Правило произведения для дивергенции гласит:

$$\nabla \cdot (u\mathbf {V} )\ =\ u\,\nabla \cdot \mathbf {V} \ +\ \nabla u\cdot \mathbf {V} .$$

Предполагать $\Omega$ является открытым ограниченным подмножеством $\mathbb {R} ^{n}$ с кусочно гладкой границей $\Gamma =\partial \Omega$. Интеграция более $\Omega$ относительно стандартной формы объема $d\Omega$и применяя теорему о дивергенции , дает:

$$\int _{\Gamma }u\mathbf {V} \cdot {\hat {\mathbf {n} }}\,d\Gamma \ =\ \int _{\Omega }\nabla \cdot (u\mathbf {V} )\,d\Omega \ =\ \int _{\Omega }u\,\nabla \cdot \mathbf {V} \,d\Omega \ +\ \int _{\Omega }\nabla u\cdot \mathbf {V} \,d\Omega ,$$

где ${\hat {\mathbf {n} }}$ - внешний единичный вектор нормали к границе, проинтегрированный относительно его стандартной римановой формы объема. $d\Gamma$. Перестановка дает:

$$\int _{\Omega }u\,\nabla \cdot \mathbf {V} \,d\Omega \ =\ \int _{\Gamma }u\mathbf {V} \cdot {\hat {\mathbf {n} }}\,d\Gamma -\int _{\Omega }\nabla u\cdot \mathbf {V} \,d\Omega ,$$

или другими словами

$$\int _{\Omega }u\,\operatorname {div} (\mathbf {V} )\,d\Omega \ =\ \int _{\Gamma }u\mathbf {V} \cdot {\hat {\mathbf {n} }}\,d\Gamma -\int _{\Omega }\operatorname {grad} (u)\cdot \mathbf {V} \,d\Omega .$$

Требования регулярности теоремы можно ослабить. Например, граница $\Gamma =\partial \Omega$ достаточно быть только липшицевым , а функции u , v должны лежать только в пространстве Соболева $H^{1}(\Omega )$.

Первая личность Грина

Рассмотрим непрерывно дифференцируемые векторные поля $\mathbf {U} =u_{1}\mathbf {e} _{1}+\cdots +u_{n}\mathbf {e} _{n}$ и $v\mathbf {e} _{1},\ldots ,v\mathbf {e} _{n}$, где $\mathbf {e} _{i}$ -й i стандартный базисный вектор для $i=1,\ldots ,n$. Теперь примените вышеуказанное интегрирование по частям к каждому $u_{i}$ раз векторное поле $v\mathbf {e} _{i}$:

$$\int _{\Omega }u_{i}{\frac {\partial v}{\partial x_{i}}}\,d\Omega \ =\ \int _{\Gamma }u_{i}v\,\mathbf {e} _{i}\cdot {\hat {\mathbf {n} }}\,d\Gamma -\int _{\Omega }{\frac {\partial u_{i}}{\partial x_{i}}}v\,d\Omega .$$

Суммирование i дает новую формулу интегрирования по частям:

$$\int _{\Omega }\mathbf {U} \cdot \nabla v\,d\Omega \ =\ \int _{\Gamma }v\mathbf {U} \cdot {\hat {\mathbf {n} }}\,d\Gamma -\int _{\Omega }v\,\nabla \cdot \mathbf {U} \,d\Omega .$$

Дело $\mathbf {U} =\nabla u$, где $u\in C^{2}({\bar {\Omega }})$, известно как первое из тождеств Грина :

$$\int _{\Omega }\nabla u\cdot \nabla v\,d\Omega \ =\ \int _{\Gamma }v\,\nabla u\cdot {\hat {\mathbf {n} }}\,d\Gamma -\int _{\Omega }v\,\nabla ^{2}u\,d\Omega .$$

См. также

• Интегрирование по частям для интеграла Лебега–Стилтьеса
• Интегрирование по частям для семимартингалов с учетом их квадратичной ковариации.
• Интегрирование путем замены
• Преобразование Лежандра

Дальнейшее чтение

• Луи Брэнд (10 октября 2013 г.). Продвинутое исчисление: введение в классический анализ . Курьерская корпорация. стр. 267–. ISBN  978-0-486-15799-3 .
• Хоффманн, Лоуренс Д.; Брэдли, Джеральд Л. (2004). Исчисление для бизнеса, экономики, социальных наук и наук о жизни (8-е изд.). стр. 450–464. ISBN  0-07-242432-Х .
• Уиллард, Стивен (1976). Исчисление и его приложения . Бостон: Приндл, Вебер и Шмидт. стр. 193–214. ISBN  0-87150-203-8 .
• Вашингтон, Аллин Дж. (1966). Техническое исчисление с аналитической геометрией . Чтение: Аддисон-Уэсли. стр. 218–245. ISBN  0-8465-8603-7 .

Внешние ссылки

• «Интегрирование по частям» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Интегрирование по частям — из MathWorld