Неопределенная форма

В исчислении обычно можно вычислить предел суммы, разности, произведения, частного или степени двух функций, взяв соответствующую комбинацию отдельных пределов каждой соответствующей функции. Например,

$${\begin{aligned}\lim _{x\to c}{\bigl (}f(x)+g(x){\bigr )}&=\lim _{x\to c}f(x)+\lim _{x\to c}g(x),\\[3mu]\lim _{x\to c}{\bigl (}f(x)g(x){\bigr )}&=\lim _{x\to c}f(x)\cdot \lim _{x\to c}g(x),\end{aligned}}$$

и то же самое для других арифметических операций; это иногда называют алгебраической предельной теоремой . Однако некоторые комбинации конкретных предельных значений не могут быть вычислены таким способом, и знание предела каждой функции в отдельности недостаточно для определения предела комбинации. Говорят, что в этих конкретных ситуациях предел принимает неопределенную форму , описываемую одним из неформальных выражений.

$${\frac {0}{0}},~{\frac {\infty }{\infty }},~0\times \infty ,~\infty -\infty ,~0^{0},~1^{\infty },{\text{ or }}\infty ^{0},$$

где каждое выражение обозначает предел функции, построенной как арифметическая комбинация двух функций, пределы которых соответственно стремятся к $0,$ $1,$ или $\infty$ как указано.

Предел, принимающий одну из этих неопределенных форм, может стремиться к нулю, может стремиться к любому конечному значению, может стремиться к бесконечности или может расходиться, в зависимости от конкретных задействованных функций. Предел, однозначно стремящийся к бесконечности, например ${\textstyle \lim _{x\to 0}1/x^{2}=\infty ,}$ не считается неопределенным. Этот термин был первоначально введен Коши учеником Муаньо в середине XIX века.

Наиболее распространенным примером неопределенной формы является частное двух функций, каждая из которых сходится к нулю. Эту неопределенную форму обозначают $0/0$. Например, как $x$ подходы $0,$ соотношения $x/x^{3}$, $x/x$, и $x^{2}/x$ пойти в $\infty$, $1$, и $0$ соответственно. В каждом случае, если подставить пределы числителя и знаменателя, результирующее выражение будет $0/0$, что является неопределенным. В этом смысле $0/0$ может принимать значения $0$, $1$, или $\infty$, путем соответствующего выбора функций для подстановки в числитель и знаменатель. Фактически можно найти пару функций, для которых пределом является любое конкретное заданное значение. Еще более удивительным, возможно, является то, что частное двух функций может фактически расходиться, а не просто расходиться до бесконечности. Например, $x\sin(1/x)/x$.

Итак, тот факт, что две функции $f(x)$ и $g(x)$ сходиться к $0$ как $x$ приближается к некоторой предельной точке $c$ недостаточно для определения предела

$\lim _{x\to c}{\frac {f(x)}{g(x)}}.$

Такую же форму неопределенной формы может иметь и выражение, возникающее иными способами, чем применение алгебраической предельной теоремы. Однако некорректно называть выражение «неопределённой формой», если выражение сделано вне контекста определения пределов.Примером может служить выражение $0^{0}$. Оставлено ли это выражение неопределенным или оно определено как равное $1$, зависит от области применения и может различаться у разных авторов. Подробнее читайте в статье Ноль в степени нуля . Обратите внимание, что $0^{\infty }$ и другие выражения, включающие бесконечность, не являются неопределенными формами .

Некоторые примеры и не примеры

Неопределенная форма 0/0

«0/0» перенаправляется сюда. Чтобы узнать об этом символе, см. Знак процента .

• 
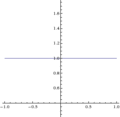
  Рис. 1: у = х / х
• 
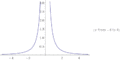
  Рис. 2: у = х ² / х
• 
  Рис. 3: у = без х / х
• 
  Рис. 4: у = х - 49 / √ х - 7 (для х = 49)
• 
  Рис. 5: у = а х / х, где а = 2
• 
  Рис. 6: у = х / х ³

Неопределенная форма $0/0$ особенно распространен в исчислении , поскольку часто возникает при оценке производных с использованием их определения в терминах предела.

Как упоминалось выше,

$\lim _{x\to 0}{\frac {x}{x}}=1,\qquad$ (см. рис. 1)

пока

$\lim _{x\to 0}{\frac {x^{2}}{x}}=0,\qquad$ (см. рис. 2)

Этого достаточно, чтобы показать, что $0/0$ является неопределенной формой. Другие примеры этой неопределенной формы включают:

$\lim _{x\to 0}{\frac {\sin(x)}{x}}=1,\qquad$ (см. рис. 3)

и

$\lim _{x\to 49}{\frac {x-49}{{\sqrt {x}}\,-7}}=14,\qquad$ (см. рис. 4)

Прямая замена числа, которое $x$ подходы к любому из этих выражений показывают, что эти примеры соответствуют неопределенной форме $0/0$, но эти пределы могут принимать множество разных значений. Любое желаемое значение $a$ для этой неопределенной формы можно получить следующим образом:

$\lim _{x\to 0}{\frac {ax}{x}}=a.\qquad$ (см. рис. 5)

Значение $\infty$ также можно получить (в смысле расходимости на бесконечность):

$\lim _{x\to 0}{\frac {x}{x^{3}}}=\infty .\qquad$ (см. рис. 6)

Неопределенная форма 0 ⁰

Основная статья: Ноль в степени нуля

График y = x ⁰

График y = 0 ^х

Следующие пределы иллюстрируют, что выражение $0^{0}$ представляет собой неопределенную форму:

$${\begin{aligned}\lim _{x\to 0^{+}}x^{0}&=1,\\\lim _{x\to 0^{+}}0^{x}&=0.\end{aligned}}$$

Таким образом, в целом, зная, что $\textstyle \lim _{x\to c}f(x)\;=\;0$ и $\textstyle \lim _{x\to c}g(x)\;=\;0$ недостаточно для оценки предела

$$\lim _{x\to c}f(x)^{g(x)}.$$

Если функции $f$ и $g$ являются аналитическими в $c$, и $f$ является положительным для $x$ достаточно близко (но не равно) к $c$, то предел $f(x)^{g(x)}$ будет $1$. В противном случае используйте преобразование из таблицы ниже, чтобы оценить предел.

Выражения, не являющиеся неопределенными формами

Выражение $1/0$ обычно не рассматривается как неопределенная форма, потому что, если предел $f/g$ существует, то нет никакой двусмысленности относительно его значения, поскольку оно всегда расходится. В частности, если $f$ подходы $1$ и $g$ подходы $0,$ затем $f$ и $g$ можно выбрать так, что:

1. $f/g$ подходы $+\infty$
2. $f/g$ подходы $-\infty$
3. Предел не существует.

В каждом случае абсолютное значение $|f/g|$ подходы $+\infty$, и поэтому частное $f/g$ должны расходиться, в смысле расширенных действительных чисел (в рамках проективно расширенной вещественной линии пределом является беззнаковая бесконечность $\infty$ во всех трёх случаях ). Аналогично любое выражение вида $a/0$ с $a\neq 0$ (включая $a=+\infty$ и $a=-\infty$) не является неопределенной формой, поскольку частное, порождающее такое выражение, всегда будет расходиться.

Выражение $0^{\infty }$ не является неопределенной формой. Выражение $0^{+\infty }$ полученное в результате рассмотрения $\lim _{x\to c}f(x)^{g(x)}$ дает предел $0,$ при условии, что $f(x)$ остается неотрицательным, так как $x$ подходы $c$. Выражение $0^{-\infty }$ аналогично эквивалентно $1/0$; если $f(x)>0$ как $x$ подходы $c$, предел получается как $+\infty$.

Чтобы понять, почему, позвольте $L=\lim _{x\to c}f(x)^{g(x)},$ где $\lim _{x\to c}{f(x)}=0,$ и $\lim _{x\to c}{g(x)}=\infty .$ Взяв натуральный логарифм обеих частей и используя $\lim _{x\to c}\ln {f(x)}=-\infty ,$ мы поняли это $\ln L=\lim _{x\to c}({g(x)}\times \ln {f(x)})=\infty \times {-\infty }=-\infty ,$ это означает, что $L={e}^{-\infty }=0.$

Оценка неопределённых форм

Прилагательное неопределенное не означает , что предела не существует, как показывают многие приведенные выше примеры. Во многих случаях алгебраическое исключение, правило Лопиталя для манипулирования выражением и вычисления предела можно использовать или другие методы.

Эквивалент бесконечно малого

Когда две переменные $\alpha$ и $\beta$ сходятся к нулю в одной и той же предельной точке и $\textstyle \lim {\frac {\beta }{\alpha }}=1$, они называются эквивалентными бесконечно малыми (экв. $\alpha \sim \beta$).

Более того, если переменные $\alpha '$ и $\beta '$ таковы, что $\alpha \sim \alpha '$ и $\beta \sim \beta '$, затем:

$\lim {\frac {\beta }{\alpha }}=\lim {\frac {\beta '}{\alpha '}}$

Вот краткое доказательство:

Предположим, что существуют две эквивалентные бесконечно малые величины $\alpha \sim \alpha '$ и $\beta \sim \beta '$.

$$\lim {\frac {\beta }{\alpha }}=\lim {\frac {\beta \beta '\alpha '}{\beta '\alpha '\alpha }}=\lim {\frac {\beta }{\beta '}}\lim {\frac {\alpha '}{\alpha }}\lim {\frac {\beta '}{\alpha '}}=\lim {\frac {\beta '}{\alpha '}}$$

Для оценки неопределенной формы $0/0$, можно использовать следующие факты об эквивалентных бесконечно малых (например, $x\sim \sin x$ если x становится ближе к нулю):

$x\sim \sin x,$

$x\sim \arcsin x,$

$x\sim \sinh x,$

$x\sim \tan x,$

$x\sim \arctan x,$

$x\sim \ln(1+x),$

$1-\cos x\sim {\frac {x^{2}}{2}},$

$\cosh x-1\sim {\frac {x^{2}}{2}},$

$a^{x}-1\sim x\ln a,$

$e^{x}-1\sim x,$

$(1+x)^{a}-1\sim ax.$

Например:

$${\begin{aligned}\lim _{x\to 0}{\frac {1}{x^{3}}}\left[\left({\frac {2+\cos x}{3}}\right)^{x}-1\right]&=\lim _{x\to 0}{\frac {e^{x\ln {\frac {2+\cos x}{3}}}-1}{x^{3}}}\\&=\lim _{x\to 0}{\frac {1}{x^{2}}}\ln {\frac {2+\cos x}{3}}\\&=\lim _{x\to 0}{\frac {1}{x^{2}}}\ln \left({\frac {\cos x-1}{3}}+1\right)\\&=\lim _{x\to 0}{\frac {\cos x-1}{3x^{2}}}\\&=\lim _{x\to 0}-{\frac {x^{2}}{6x^{2}}}\\&=-{\frac {1}{6}}\end{aligned}}$$

Во 2-м равенстве $e^{y}-1\sim y$ где $y=x\ln {2+\cos x \over 3}$ по мере того, как y становится ближе к 0, и используется $y\sim \ln {(1+y)}$ где $y={{\cos x-1} \over 3}$ используется в 4-м равенстве, а $1-\cos x\sim {x^{2} \over 2}$ используется в пятом равенстве.

Правило Лопиталя

Основная статья: Правило Лопиталя

Правило Лопиталя — общий метод оценки неопределенных форм. $0/0$ и $\infty /\infty$. Это правило гласит, что (при соответствующих условиях)

$\lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {f'(x)}{g'(x)}},$

где $f'$ и $g'$ являются производными от $f$ и $g$. (Обратите внимание, что это правило не распространяется на выражения $\infty /0$, $1/0$и т. д., поскольку эти выражения не являются неопределенными формами.) Эти производные позволят выполнить алгебраическое упрощение и в конечном итоге оценить предел.

Правило Лопиталя можно применить и к другим неопределенным формам, предварительно применив соответствующее алгебраическое преобразование. Например, чтобы оценить форму 0 ⁰ :

$\ln \lim _{x\to c}f(x)^{g(x)}=\lim _{x\to c}{\frac {\ln f(x)}{1/g(x)}}.$

Правая часть имеет вид $\infty /\infty$, поэтому к нему применимо правило Лопиталя. Обратите внимание, что это уравнение справедливо (пока определена правая часть), поскольку натуральный логарифм (ln) является непрерывной функцией ; не имеет значения, насколько хорошо себя ведут $f$ и $g$ может (а может и не быть) до тех пор, пока $f$ является асимптотически положительной. (область логарифмов — это совокупность всех положительных действительных чисел.)

Хотя правило Лопиталя применимо к обоим $0/0$ и $\infty /\infty$, одна из этих форм может оказаться полезнее другой в конкретном случае (из-за возможности последующего алгебраического упрощения). Между этими формами можно переключаться, преобразуя $f/g$ к $(1/g)/(1/f)$.

Список неопределенных форм

В следующей таблице перечислены наиболее распространенные неопределенные формы и преобразования для применения правила Лопиталя.

Неопределенная форма	Условия	Преобразование в $0/0$	Преобразование в $\infty /\infty$
$0$/ $0$	$\lim _{x\to c}f(x)=0,\ \lim _{x\to c}g(x)=0\!$	—	$\lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {1/g(x)}{1/f(x)}}\!$
$\infty$/ $\infty$	$\lim _{x\to c}f(x)=\infty ,\ \lim _{x\to c}g(x)=\infty \!$	$\lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {1/g(x)}{1/f(x)}}\!$	—
$0\cdot \infty$	$\lim _{x\to c}f(x)=0,\ \lim _{x\to c}g(x)=\infty \!$	$\lim _{x\to c}f(x)g(x)=\lim _{x\to c}{\frac {f(x)}{1/g(x)}}\!$	$\lim _{x\to c}f(x)g(x)=\lim _{x\to c}{\frac {g(x)}{1/f(x)}}\!$
$\infty -\infty$	$\lim _{x\to c}f(x)=\infty ,\ \lim _{x\to c}g(x)=\infty \!$	$\lim _{x\to c}(f(x)-g(x))=\lim _{x\to c}{\frac {1/g(x)-1/f(x)}{1/(f(x)g(x))}}\!$	$\lim _{x\to c}(f(x)-g(x))=\ln \lim _{x\to c}{\frac {e^{f(x)}}{e^{g(x)}}}\!$
$0^{0}$	$\lim _{x\to c}f(x)=0^{+},\lim _{x\to c}g(x)=0\!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {g(x)}{1/\ln f(x)}}\!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {\ln f(x)}{1/g(x)}}\!$
$1^{\infty }$	$\lim _{x\to c}f(x)=1,\ \lim _{x\to c}g(x)=\infty \!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {\ln f(x)}{1/g(x)}}\!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {g(x)}{1/\ln f(x)}}\!$
$\infty ^{0}$	$\lim _{x\to c}f(x)=\infty ,\ \lim _{x\to c}g(x)=0\!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {g(x)}{1/\ln f(x)}}\!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {\ln f(x)}{1/g(x)}}\!$

См. также

• Определенный и неопределенный
• Деление на ноль
• Расширенная строка действительных чисел
• Неопределенное уравнение
• Неопределенная система
• Неопределенный (переменный)
• Правило больницы

Ссылки

Библиографии

• Варберг, Дейл Э.; Перселл, Эдвин Дж.; Ригдон, Стивен Э. (2007). Исчисление (9-е изд.). Пирсон Прентис Холл . ISBN  978-0131469686 .