Секущая линия

Чтобы узнать о секущей тригонометрической функции, см. Секущая (тригонометрия) .

В геометрии секущая линия — это , пересекающая кривую как минимум в двух различных точках . Слово секанс происходит от латинского слова secare , что означает разрезать . В случае круга секущая пересекает круг ровно в двух точках. Хорда отрезок — это прямой, определяемый двумя точками, то есть отрезок секущей, концами которого являются две точки.

Круги

Дополнительная информация: Круг § Хорда.

Общие прямые и отрезки окружности, включая секущую.

Прямая может пересекать окружность в нуле, одной или двух точках. Линия с пересечениями в двух точках называется секущей , в одной точке - касательной и ни в одной точке - внешней линией . Хорда — это отрезок линии, соединяющий две различные точки окружности. Таким образом, хорда содержится в уникальной секущей линии, и каждая секущая линия определяет уникальную хорду.

В строгих современных трактовках геометрии плоскостей результаты, которые кажутся очевидными и были приняты (без формулировок) Евклидом в его трактовке обычно доказываются .

Например, Теорема (Элементарная круговая непрерывность) : Если ${\mathcal {C}}$ представляет собой круг и $\ell$ линия, содержащая точку А, находящуюся внутри ${\mathcal {C}}$ и точка B, находящаяся за пределами ${\mathcal {C}}$ затем $\ell$ является секущей линией для ${\mathcal {C}}$.

В некоторых ситуациях формулировка результатов в виде секущих линий вместо аккордов может помочь унифицировать высказывания. В качестве примера рассмотрим результат:

Если две секущие линии содержат хорды AB и CD в окружности и пересекаются в точке P , не принадлежащей окружности, то длины отрезков удовлетворяют условию AP ⋅ PB = CP ⋅ PD .

Если точка P лежит внутри круга, это Евклид III.35, но если точка находится вне круга, результат не содержится в Элементах. Однако Роберт Симсон вслед за Кристофером Клавиусом продемонстрировал этот результат, иногда называемый теоремой о пересекающихся секущих , в своих комментариях к Евклиду.

Кривые

Для кривых, более сложных, чем простые круги, возникает возможность того, что линия пересекает кривую более чем в двух различных точках. Некоторые авторы определяют секущую линию кривой как линию, пересекающую кривую в двух различных точках. Это определение оставляет открытой возможность того, что линия может иметь и другие точки пересечения с кривой. В такой формулировке определения секущей линии для кругов и кривых идентичны, и для круга возможность дополнительных точек пересечения просто не возникает.

Секущие и касательные

Секущие могут использоваться для аппроксимации касательной , если к кривой в некоторой точке P она существует. Определите секущую кривой по двум P точкам и Q с фиксированным P и Q. переменной Когда Q приближается к P вдоль кривой, если наклон секущей приближается к значению , то этот предел определяет наклон касательной в точке P. предельному Секущие линии PQ являются приближениями касательной. В исчислении эта идея представляет собой геометрическое определение производной .

Касательная линия в точке P является секущей кривой.

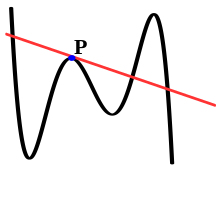
Касательная линия к кривой в точке P может быть секущей линией к этой кривой, если она пересекает кривую хотя бы в одной точке, кроме P . Другой способ взглянуть на это — осознать, что быть касательной линией в точке P — это локальное свойство, зависящее только от кривой в непосредственной близости от точки P , тогда как быть секущей линией — это глобальное свойство, поскольку вся область определения необходимо изучить функцию, производящую кривую.

Множества и n -секущие

Понятие секущей линии может быть применено в более общем контексте, чем евклидово пространство. Пусть K — конечное множество из k точек в некоторой геометрической ситуации. Прямая называется n -секущей K если она содержит ровно n точек K. , Например, если K — это набор из 50 точек, расположенных на окружности в евклидовой плоскости, линия, соединяющая две из них, будет 2-секущей (или биссектрисой ), а линия, проходящая через только одну из них, будет 1-. секущая (или унисекс ). Унисекс в этом примере не обязательно должен быть касательной к окружности.

Эта терминология часто используется в геометрии падения и дискретной геометрии . Например, теорема Сильвестра-Галлаи о геометрии инцидентности утверждает, что если n точек евклидовой геометрии не лежат на одной прямой , то из них должна существовать 2-секущая. А исходная задача дискретной геометрии о посадке фруктовых садов требует ограничения количества 3-секущих конечного набора точек.

Конечность множества точек не является существенной в этом определении, поскольку каждая прямая может пересекать множество только в конечном числе точек.

См. также

• Эллиптическая кривая — кривая, у которой каждая секущая имеет третью точку пересечения, из которой можно определить большую часть группового закона.
• Теорема о среднем значении , согласно которой каждая секущая графика гладкой функции имеет параллельную касательную.
• Квадрисеканс — линия, пересекающая четыре точки кривой (обычно пространственной кривой).
• Секущая плоскость , трехмерный эквивалент секущей линии.
• Секущее многообразие , объединение секущих и касательных линий к заданному проективному многообразию.

Внешние ссылки

• Вайсштейн, Эрик В. «Секущая линия» . Математический мир .