Правило больницы

Пример применения правила Лопиталя к ж ( Икс ) знак равно грех( х ) и г ( Икс ) знак равно −0,5 x : функция час ( Икс ) знак равно ж ( х ) / g ( x ) не определено в x = 0 , но может быть преобразовано в непрерывную функцию на всем R путем определения ч (0) = ж ′(0) / г ′(0) знак равно -2 .

Правило Лопиталя ( / ˌ l oʊ p iː ˈ t ɑː l / , loh-pee- TAHL ) или правило Лопиталя , также известное как правило Бернулли , — математическая теорема, позволяющая оценивать пределы с неопределённых форм помощью производных . Применение (или повторное применение) правила часто преобразует неопределенную форму в выражение, которое можно легко вычислить путем подстановки. Правило названо в честь французского математика 17 века Гийома Де Л'Опиталя . Хотя это правило часто приписывают Де Лопиталю, теорема была впервые представлена ​​ему в 1694 году швейцарским математиком Иоганном Бернулли .

Правило Лопиталя гласит, что для функций f и g , определенных на открытом интервале I и дифференцируемых на ${\textstyle I\setminus \{c\}}$ бесконечной) точки накопления c I для (возможно , , если ${\textstyle \lim \limits _{x\to c}f(x)=\lim \limits _{x\to c}g(x)=0{\text{ or }}\pm \infty ,}$ и ${\textstyle g'(x)\neq 0}$ для всех x в I с x ≠ c и ${\textstyle \lim \limits _{x\to c}{\frac {f'(x)}{g'(x)}}}$ существует, то

$\lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {f'(x)}{g'(x)}}.$

Дифференцирование числителя и знаменателя часто упрощает частное или преобразует его в предел, который можно вычислить напрямую.

История

Гийом де Л'Опиталь (также пишется как l'Hospital ) опубликовал это правило в своей книге 1696 года «Analyze des Infiniment Petits pour l’Intelligence des Lignes Courbes» (дословный перевод: «Анализ бесконечно малого для понимания кривых линий »), первом учебнике по дифференциальному исчислению . Однако считается, что правило открыл швейцарский математик Иоганн Бернулли .

Общая форма

Общая форма правила Лопиталя охватывает множество случаев. Пусть c и L — расширенные действительные числа (т. е. действительные числа, положительная бесконечность или отрицательная бесконечность). Пусть I — открытый интервал, содержащий c (для двустороннего предела), или открытый интервал с конечной точкой c (для одностороннего предела или предел на бесконечности , если c бесконечно). действительные функции f и g Предполагается, что дифференцируемы по I, за исключением, возможно, точки c , и, кроме того, $g'(x)\neq 0$ на I, за исключением, возможно, c . Также предполагается, что ${\textstyle \lim \limits _{x\to c}{\frac {f'(x)}{g'(x)}}=L.}$ Таким образом, правило применяется к ситуациям, в которых соотношение производных имеет конечный или бесконечный предел, но не к ситуациям, в которых это соотношение постоянно колеблется по мере того, как x становится все ближе и ближе к c .

Если либо $$\lim _{x\to c}f(x)=\lim _{x\to c}g(x)=0$$или $$\lim _{x\to c}|f(x)|=\lim _{x\to c}|g(x)|=\infty ,$$затем $$\lim _{x\to c}{\frac {f(x)}{g(x)}}=L.$$Хотя мы повсюду писали x → c , пределы могут быть и односторонними ( x → c ⁺ или х → с ⁻ ), когда c — конечная точка I .

Во втором случае гипотеза о f стремлении к бесконечности при доказательстве не используется (см. примечание в конце раздела доказательства); таким образом, хотя условия правила обычно формулируются, как указано выше, второе достаточное условие для того, чтобы процедура правила была действительной, может быть сформулирована более кратко как ${\textstyle \lim _{x\to c}|g(x)|=\infty .}$

Гипотеза о том, что $g'(x)\neq 0$ чаще всего встречается в литературе, но некоторые авторы обходят эту гипотезу, добавляя другие гипотезы в других местах. Один метод заключается в определении предела функции с дополнительным требованием, чтобы предельная функция была определена всюду на соответствующем интервале I, за исключением, возможно, точки c . Другой метод состоит в том, чтобы потребовать, чтобы и f, и g были дифференцируемы всюду на интервале, содержащем c .

Случаи, когда теорему нельзя применить (Необходимость условий)

Все четыре условия правила Лопиталя необходимы:

1. Неопределенность формы: $\lim _{x\to c}f(x)=\lim _{x\to c}g(x)=0$ или $\pm \infty$ ; и
2. Дифференцируемость функций: $f(x)$ и $g(x)$ дифференцируемы открытом на интервале ${\mathcal {I}}$ кроме, возможно, в какой-то момент $c$ содержится в ${\mathcal {I}}$ (та же точка из предела) ; и
3. Ненулевая производная знаменателя: $g'(x)\neq 0$ для всех $x$ в ${\mathcal {I}}$ с $x\neq c$ ; и
4. Существование предела частного производных: $\lim _{x\to c}{\frac {f'(x)}{g'(x)}}$ существует.

Если одно из вышеуказанных условий не выполнено, правило Лопиталя вообще недействительно и поэтому не всегда может быть применено.

Форма не является неопределенной

В необходимости первого условия можно убедиться, рассмотрев контрпример, в котором функции имеют вид $f(x)=x+1$ и $g(x)=2x+1$ и предел $x\to 1$.

Первое условие для этого контрпримера не выполняется, поскольку $\lim _{x\to 1}f(x)=\lim _{x\to 1}(x+1)=(1)+1=2\neq 0$ и $\lim _{x\to 1}g(x)=\lim _{x\to 1}(2x+1)=2(1)+1=3\neq 0$. Это означает, что форма не является неопределенной.

Второе и третье условия удовлетворяются $f(x)$ и $g(x)$. Четвертое условие также удовлетворяется $\lim _{x\to 1}{\frac {f'(x)}{g'(x)}}=\lim _{x\to 1}{\frac {(x+1)'}{(2x+1)'}}=\lim _{x\to 1}{\frac {1}{2}}={\frac {1}{2}}$.

Но правило Лопиталя в этом контрпримере не работает, поскольку $\lim _{x\to 1}{\frac {f(x)}{g(x)}}=\lim _{x\to 1}{\frac {x+1}{2x+1}}={\frac {\lim _{x\to 1}(x+1)}{\lim _{x\to 1}(2x+1)}}={\frac {2}{3}}\neq {\frac {1}{2}}=\lim _{x\to 1}{\frac {f'(x)}{g'(x)}}$.

Дифференцируемость функций

Дифференцируемость функций является обязательным требованием, поскольку, если функция не дифференцируема, то не гарантируется существование производной функции в каждой точке. ${\mathcal {I}}$. Тот факт, что ${\mathcal {I}}$ является открытым интервалом, вытекающим из гипотезы теоремы Коши о среднем значении . Заметное исключение из возможности недифференцируемости функций при $c$ существует, потому что правило Лопиталя требует, чтобы производная существовала только при приближении функции $c$; производную не обязательно брать $c$.

Например, пусть $f(x)={\begin{cases}\sin x,&x\neq 0\\1,&x=0\end{cases}}$ , $g(x)=x$, и $c=0$. В этом случае, $f(x)$ не дифференцируема при $c$. Однако, поскольку $f(x)$ дифференцируемо всюду, кроме $c$, затем $\lim _{x\to c}f'(x)$ все еще существует. Таким образом, поскольку

$\lim _{x\to c}{\frac {f(x)}{g(x)}}={\frac {0}{0}}$ и $\lim _{x\to c}{\frac {f'(x)}{g'(x)}}$ существует, правило Лопиталя остается в силе.

Производная знаменателя равна нулю

Необходимость условия, $g'(x)\neq 0$ около $c$ можно увидеть на следующем контрпримере, принадлежащем Отто Штольцу . Позволять $f(x)=x+\sin x\cos x$ и $g(x)=f(x)e^{\sin x}.$ Тогда нет предела $f(x)/g(x)$ как $x\to \infty .$ Однако,

${\begin{aligned}{\frac {f'(x)}{g'(x)}}&={\frac {2\cos ^{2}x}{(2\cos ^{2}x)e^{\sin x}+(x+\sin x\cos x)e^{\sin x}\cos x}}\\&={\frac {2\cos x}{2\cos x+x+\sin x\cos x}}e^{-\sin x},\end{aligned}}$

который стремится к 0, так как $x\to \infty$. Дальнейшие примеры этого типа были найдены Ральфом П. Боасом-младшим.

Предела деривативов не существует

Требование о том, чтобы предел

$\lim _{x\to c}{\frac {f'(x)}{g'(x)}}$

существует, имеет важное значение. Без этого условия $f'$ или $g'$ может проявлять незатухающие колебания, так как $x$ подходы $c$, и в этом случае правило Лопиталя не применяется. Например, если $f(x)=x+\sin(x)$, $g(x)=x$ и $c=\pm \infty$, затем

${\frac {f'(x)}{g'(x)}}={\frac {1+\cos(x)}{1}};$

это выражение не приближается к пределу, поскольку $x$ идет в $c$, поскольку функция косинуса колеблется между 1 и −1 . Но работая с оригинальными функциями, $\lim _{x\to \infty }{\frac {f(x)}{g(x)}}$ можно доказать существование:

$\lim _{x\to \infty }{\frac {f(x)}{g(x)}}=\lim _{x\to \infty }\left({\frac {x+\sin(x)}{x}}\right)=\lim _{x\to \infty }\left(1+{\frac {\sin(x)}{x}}\right)=1+\lim _{x\to \infty }\left({\frac {\sin(x)}{x}}\right)=1+0=1.$

В таком случае можно сделать только один вывод:

$\liminf _{x\to c}{\frac {f'(x)}{g'(x)}}\leq \liminf _{x\to c}{\frac {f(x)}{g(x)}}\leq \limsup _{x\to c}{\frac {f(x)}{g(x)}}\leq \limsup _{x\to c}{\frac {f'(x)}{g'(x)}},$

так что если предел ${\textstyle {\frac {f}{g}}}$ f / g существует, то оно должно лежать между нижним и верхним пределами ${\textstyle {\frac {f'}{g'}}}$ . (В приведенном выше примере это верно, поскольку 1 действительно находится между 0 и 2.)

Примеры

• Вот базовый пример показательной функции, которая имеет неопределенную форму. ⁠ 0/0 ​ ⁠ = в x 0 : $${\begin{aligned}\lim _{x\to 0}{\frac {e^{x}-1}{x^{2}+x}}&=\lim _{x\to 0}{\frac {{\frac {d}{dx}}(e^{x}-1)}{{\frac {d}{dx}}(x^{2}+x)}}\\[4pt]&=\lim _{x\to 0}{\frac {e^{x}}{2x+1}}\\[4pt]&=1.\end{aligned}}$$
• Это более подробный пример, включающий ⁠ 0 / 0 ⁠ . Применение правила Лопиталя один раз все равно приводит к неопределенной форме. В этом случае предел можно оценить, применив правило трижды: $${\begin{aligned}\lim _{x\to 0}{\frac {2\sin(x)-\sin(2x)}{x-\sin(x)}}&=\lim _{x\to 0}{\frac {2\cos(x)-2\cos(2x)}{1-\cos(x)}}\\[4pt]&=\lim _{x\to 0}{\frac {-2\sin(x)+4\sin(2x)}{\sin(x)}}\\[4pt]&=\lim _{x\to 0}{\frac {-2\cos(x)+8\cos(2x)}{\cos(x)}}\\[4pt]&={\frac {-2+8}{1}}\\[4pt]&=6.\end{aligned}}$$
• Вот пример, включающий ⁠ ∞ / ∞ ⁠ : $$\lim _{x\to \infty }x^{n}\cdot e^{-x}=\lim _{x\to \infty }{\frac {x^{n}}{e^{x}}}=\lim _{x\to \infty }{\frac {nx^{n-1}}{e^{x}}}=n\cdot \lim _{x\to \infty }{\frac {x^{n-1}}{e^{x}}}.$$ Неоднократно применяйте правило Лопиталя до тех пор, пока показатель степени не станет нулевым (если n целое число) или отрицательным (если n дробное), чтобы сделать вывод, что предел равен нулю.
• Вот пример неопределенной формы 0 · ∞ (см. ниже), которая переписывается как форма ⁠ ∞ / ∞ ⁠ : $$\lim _{x\to 0^{+}}x\ln x=\lim _{x\to 0^{+}}{\frac {\ln x}{\frac {1}{x}}}=\lim _{x\to 0^{+}}{\frac {\frac {1}{x}}{-{\frac {1}{x^{2}}}}}=\lim _{x\to 0^{+}}-x=0.$$
• Вот пример формулы погашения ипотечного кредита и ⁠ 0 / 0 ⁠ . Пусть P — основная сумма кредита (сумма кредита), r — процентная ставка за период, а n — количество периодов. Когда r равно нулю, сумма погашения за период равна ${\frac {P}{n}}$ (так как погашается только основная сумма долга); это соответствует формуле для ненулевых процентных ставок: $${\begin{aligned}\lim _{r\to 0}{\frac {Pr(1+r)^{n}}{(1+r)^{n}-1}}&=P\lim _{r\to 0}{\frac {(1+r)^{n}+rn(1+r)^{n-1}}{n(1+r)^{n-1}}}\\[4pt]&={\frac {P}{n}}.\end{aligned}}$$
• Можно также использовать правило Лопиталя для доказательства следующей теоремы. Если f дважды дифференцируема в окрестности точки x и ее вторая производная непрерывна в этой окрестности, то $${\begin{aligned}\lim _{h\to 0}{\frac {f(x+h)+f(x-h)-2f(x)}{h^{2}}}&=\lim _{h\to 0}{\frac {f'(x+h)-f'(x-h)}{2h}}\\[4pt]&=\lim _{h\to 0}{\frac {f''(x+h)+f''(x-h)}{2}}\\[4pt]&=f''(x).\end{aligned}}$$

• Иногда правило Лопиталя применяется хитрым способом: предположим, $f(x)+f'(x)$ сходится при x → ∞ и что $e^{x}\cdot f(x)$ сходится к положительной или отрицательной бесконечности. Затем:

  $$\lim _{x\to \infty }f(x)=\lim _{x\to \infty }{\frac {e^{x}\cdot f(x)}{e^{x}}}=\lim _{x\to \infty }{\frac {e^{x}{\bigl (}f(x)+f'(x){\bigr )}}{e^{x}}}=\lim _{x\to \infty }{\bigl (}f(x)+f'(x){\bigr )}$$ и так, ${\textstyle \lim _{x\to \infty }f(x)}$ существует и ${\textstyle \lim _{x\to \infty }f'(x)=0.}$

  Результат остается верным без дополнительной гипотезы о том, что $e^{x}\cdot f(x)$ сходится к положительной или отрицательной бесконечности, но обоснование тогда является неполным.

Осложнения

Иногда правило Лопиталя не приводит к ответу за конечное число шагов, если не применяются некоторые дополнительные шаги. Примеры включают следующее:

• Два приложения могут привести к возврату к исходному выражению, которое должно было быть вычислено: $$\lim _{x\to \infty }{\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}=\lim _{x\to \infty }{\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}=\lim _{x\to \infty }{\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}=\cdots .$$ Эту ситуацию можно решить, заменив $y=e^{x}$ и отмечая, что y стремится к бесконечности, как x стремится к бесконечности; при такой замене эту проблему можно решить однократным применением правила: $$\lim _{x\to \infty }{\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}=\lim _{y\to \infty }{\frac {y+y^{-1}}{y-y^{-1}}}=\lim _{y\to \infty }{\frac {1-y^{-2}}{1+y^{-2}}}={\frac {1}{1}}=1.$$ Альтернативно, числитель и знаменатель можно умножить на $e^{x},$ в этот момент правило Лопиталя может быть немедленно успешно применено: $$\lim _{x\to \infty }{\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}=\lim _{x\to \infty }{\frac {e^{2x}+1}{e^{2x}-1}}=\lim _{x\to \infty }{\frac {2e^{2x}}{2e^{2x}}}=1.$$
• Сколь угодно большое количество обращений может никогда не привести к ответу, даже без повторения: $$\lim _{x\to \infty }{\frac {x^{\frac {1}{2}}+x^{-{\frac {1}{2}}}}{x^{\frac {1}{2}}-x^{-{\frac {1}{2}}}}}=\lim _{x\to \infty }{\frac {{\frac {1}{2}}x^{-{\frac {1}{2}}}-{\frac {1}{2}}x^{-{\frac {3}{2}}}}{{\frac {1}{2}}x^{-{\frac {1}{2}}}+{\frac {1}{2}}x^{-{\frac {3}{2}}}}}=\lim _{x\to \infty }{\frac {-{\frac {1}{4}}x^{-{\frac {3}{2}}}+{\frac {3}{4}}x^{-{\frac {5}{2}}}}{-{\frac {1}{4}}x^{-{\frac {3}{2}}}-{\frac {3}{4}}x^{-{\frac {5}{2}}}}}=\cdots .$$Эту ситуацию также можно решить путем преобразования переменных, в данном случае $y={\sqrt {x}}$: $$\lim _{x\to \infty }{\frac {x^{\frac {1}{2}}+x^{-{\frac {1}{2}}}}{x^{\frac {1}{2}}-x^{-{\frac {1}{2}}}}}=\lim _{y\to \infty }{\frac {y+y^{-1}}{y-y^{-1}}}=\lim _{y\to \infty }{\frac {1-y^{-2}}{1+y^{-2}}}={\frac {1}{1}}=1.$$ Опять же, альтернативный подход — умножить числитель и знаменатель на $x^{1/2}$ перед применением правила Лопиталя: $$\lim _{x\to \infty }{\frac {x^{\frac {1}{2}}+x^{-{\frac {1}{2}}}}{x^{\frac {1}{2}}-x^{-{\frac {1}{2}}}}}=\lim _{x\to \infty }{\frac {x+1}{x-1}}=\lim _{x\to \infty }{\frac {1}{1}}=1.$$

Распространенной ошибкой является использование правила Лопиталя с некоторыми круговыми рассуждениями для вычисления производной через разностный коэффициент . Например, рассмотрим задачу доказательства формулы производной для степеней x :

$\lim _{h\to 0}{\frac {(x+h)^{n}-x^{n}}{h}}=nx^{n-1}.$

Применяя правило Лопиталя и находя производные по h числителя и знаменателя, получаем нх ^{п -1} как и ожидалось. Однако дифференцирование числителя требует использования самого доказываемого факта. Это пример постановки вопроса , поскольку нельзя предполагать, что факт будет доказан в ходе доказательства.

Аналогичная ошибка возникает при расчете $\lim _{x\to 0}{\frac {\sin(x)}{x}}=1.$ Доказывая, что дифференцирование $\sin(x)$ дает $\cos(x)$ включает в себя вычисление коэффициента разницы $\lim _{h\to 0}{\frac {\sin(h)}{h}}$ другой метод, например, теорему о сжатии во-первых, поэтому вместо этого необходимо использовать .

Другие неопределенные формы

Другие неопределенные формы, такие как 1 ^∞ , 0 ⁰ , ∞ ⁰ , 0 · ∞ и ∞ − ∞ иногда можно оценить с помощью правила Лопиталя. Например, чтобы вычислить предел, включающий ∞ − ∞ , преобразуйте разницу двух функций в частное:

${\begin{aligned}\lim _{x\to 1}\left({\frac {x}{x-1}}-{\frac {1}{\ln x}}\right)&=\lim _{x\to 1}{\frac {x\cdot \ln x-x+1}{(x-1)\cdot \ln x}}&\quad (1)\\[6pt]&=\lim _{x\to 1}{\frac {\ln x}{{\frac {x-1}{x}}+\ln x}}&\quad (2)\\[6pt]&=\lim _{x\to 1}{\frac {x\cdot \ln x}{x-1+x\cdot \ln x}}&\quad (3)\\[6pt]&=\lim _{x\to 1}{\frac {1+\ln x}{1+1+\ln x}}&\quad (4)\\[6pt]&=\lim _{x\to 1}{\frac {1+\ln x}{2+\ln x}}\\[6pt]&={\frac {1}{2}},\end{aligned}}$

где правило Лопиталя применяется при переходе от (1) к (2) и снова при переходе от (3) к (4).

Правило Лопиталя можно использовать в неопределенных формах, включающих показатели степени , используя логарифмы для «перемещения показателя степени вниз». Вот пример неопределенной формы 0. ⁰ :

$\lim _{x\to 0^{+}}x^{x}=\lim _{x\to 0^{+}}e^{\ln(x^{x})}=\lim _{x\to 0^{+}}e^{x\cdot \ln x}=e^{\lim \limits _{x\to 0^{+}}(x\cdot \ln x)}.$

допустимо Перемещение предела внутри экспоненциальной функции , поскольку экспоненциальная функция непрерывна . Теперь показатель $x$ был «перемещен вниз». Предел $\lim _{x\to 0^{+}}x\cdot \ln x$ имеет неопределенную форму 0 · ∞ , но, как показано в примере выше, правило Лопиталя можно использовать для определения того, что

$\lim _{x\to 0^{+}}x\cdot \ln x=0.$

Таким образом

$\lim _{x\to 0^{+}}x^{x}=e^{0}=1.$

В следующей таблице перечислены наиболее распространенные неопределенные формы и преобразования для применения правила Лопиталя:

Неопределенная форма	Условия	Преобразование в $0/0$
⁠ 0 / 0 ⁠	$\lim _{x\to c}f(x)=0,\ \lim _{x\to c}g(x)=0\!$	—
⁠ $\infty$/ $\infty$⁠	$\lim _{x\to c}f(x)=\infty ,\ \lim _{x\to c}g(x)=\infty \!$	$\lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {1/g(x)}{1/f(x)}}\!$
$0\cdot \infty$	$\lim _{x\to c}f(x)=0,\ \lim _{x\to c}g(x)=\infty \!$	$\lim _{x\to c}f(x)g(x)=\lim _{x\to c}{\frac {f(x)}{1/g(x)}}\!$
$\infty -\infty$	$\lim _{x\to c}f(x)=\infty ,\ \lim _{x\to c}g(x)=\infty \!$	$\lim _{x\to c}(f(x)-g(x))=\lim _{x\to c}{\frac {1/g(x)-1/f(x)}{1/(f(x)g(x))}}\!$
$0^{0}$	$\lim _{x\to c}f(x)=0^{+},\lim _{x\to c}g(x)=0\!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {g(x)}{1/\ln f(x)}}\!$
$1^{\infty }$	$\lim _{x\to c}f(x)=1,\ \lim _{x\to c}g(x)=\infty \!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {\ln f(x)}{1/g(x)}}\!$
$\infty ^{0}$	$\lim _{x\to c}f(x)=\infty ,\ \lim _{x\to c}g(x)=0\!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {g(x)}{1/\ln f(x)}}\!$

Теорема Прайда – Чезаро

Основная статья: теорема Штольца – Чезаро

Теорема Штольца-Чезаро представляет собой аналогичный результат, касающийся пределов последовательностей, но в ней используются конечно- разностные операторы, а не производные .

Геометрическая интерпретация

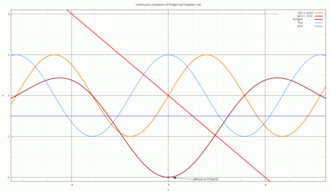
Рассмотрим кривую на плоскости, координата x которой задана g ( t ) , а координата y задана f ( t ) , причем обе функции непрерывны, т. е. геометрическое место точек вида [ g ( t ), ж ( т )] . Предположим ж ( c ) знак равно г ( c ) знак равно 0 . Предел соотношения ⁠ f ( t ) / g ( t ) ⁠ при t → c — наклон касательной к кривой в точке [ g ( c ), f ( c )] = [0,0] . Касательная к кривой в точке [ g ( t ), f ( t )] определяется выражением [ g ′( t ), f ′( t )] . Правило Лопиталя тогда гласит, что наклон кривой при t = c является пределом наклона касательной к кривой, когда кривая приближается к началу координат, при условии, что это определено.

Доказательство правления Лопиталя

Особый случай

Доказательство правила Лопиталя простое в случае, когда f и g в непрерывно дифференцируемы точке c и когда конечный предел находится после первого раунда дифференцирования. Это не доказательство общего правила Лопиталя, поскольку оно более строгое по своему определению, требующее как непрерывной дифференцируемости, так и того, чтобы c было действительным числом. Поскольку многие распространенные функции имеют непрерывные производные (например, полиномы , синус и косинус , показательные функции ), это особый случай, заслуживающий внимания.

Предположим, что f и g непрерывно дифференцируемы по действительному числу c , что $f(c)=g(c)=0$, и это $g'(c)\neq 0$. Затем

${\begin{aligned}&\lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {f(x)-0}{g(x)-0}}=\lim _{x\to c}{\frac {f(x)-f(c)}{g(x)-g(c)}}\\[6pt]={}&\lim _{x\to c}{\frac {\left({\frac {f(x)-f(c)}{x-c}}\right)}{\left({\frac {g(x)-g(c)}{x-c}}\right)}}={\frac {\lim \limits _{x\to c}\left({\frac {f(x)-f(c)}{x-c}}\right)}{\lim \limits _{x\to c}\left({\frac {g(x)-g(c)}{x-c}}\right)}}={\frac {f'(c)}{g'(c)}}=\lim _{x\to c}{\frac {f'(x)}{g'(x)}}.\end{aligned}}$

Это следует из определения производной с помощью разностного фактора. Последнее равенство следует из непрерывности производных в точке c . Предел в заключении не является неопределенным, поскольку $g'(c)\neq 0$.

Доказательство более общей версии правила Лопиталя приведено ниже.

Общее доказательство

Следующее доказательство принадлежит Тейлору (1952) , где было приведено единое доказательство для ${\textstyle {\frac {0}{0}}}$ и ${\textstyle {\frac {\pm \infty }{\pm \infty }}}$ даны неопределенные формы. Тейлор отмечает, что разные доказательства можно найти у Леттенмейера (1936) и Важевского (1949) .

Пусть f и g — функции, удовлетворяющие гипотезам раздела «Общая форма» . Позволять ${\mathcal {I}}$ быть открытым интервалом в гипотезе с конечной точкой c . Учитывая, что $g'(x)\neq 0$ на этом интервале и g непрерывен, ${\mathcal {I}}$ можно выбрать меньшим, чтобы g было отличным от нуля на ${\mathcal {I}}$.

Для каждого x в интервале определите $m(x)=\inf {\frac {f'(t)}{g'(t)}}$ и $M(x)=\sup {\frac {f'(t)}{g'(t)}}$ как $t$ колеблется по всем значениям между x и c . (Символы inf и sup обозначают нижнюю и верхнюю грань .)

Из дифференцируемости f и g по ${\mathcal {I}}$, теорема Коши о среднем значении гарантирует, что для любых двух различных точек x и y в ${\mathcal {I}}$ существует $\xi$ между x и y так, что ${\frac {f(x)-f(y)}{g(x)-g(y)}}={\frac {f'(\xi )}{g'(\xi )}}$. Следовательно, $m(x)\leq {\frac {f(x)-f(y)}{g(x)-g(y)}}\leq M(x)$ для всех вариантов выбора различных x и y в интервале. Значение g ( x )-g ( y ) всегда отлично от нуля для различных x и y в интервале, поскольку в противном случае теорема о среднем значении подразумевала бы существование p между x и y такого, что g' ( p )=0.

Определение m ( x ) и M ( x ) приведет к расширенному действительному числу, и поэтому они могут принимать значения ± ∞. В следующих двух случаях m ( x ) и M ( x ) установят границы отношения ⁠ f / g ⁠ .

Случай 1: $\lim _{x\to c}f(x)=\lim _{x\to c}g(x)=0$

Для любого x в интервале ${\mathcal {I}}$, и точка y между x и c ,

$m(x)\leq {\frac {f(x)-f(y)}{g(x)-g(y)}}={\frac {{\frac {f(x)}{g(x)}}-{\frac {f(y)}{g(x)}}}{1-{\frac {g(y)}{g(x)}}}}\leq M(x)$

и поэтому, когда y приближается к c , ${\frac {f(y)}{g(x)}}$ и ${\frac {g(y)}{g(x)}}$ станет нулем, и так

$m(x)\leq {\frac {f(x)}{g(x)}}\leq M(x).$

Случай 2: $\lim _{x\to c}|g(x)|=\infty$

Для каждого x в интервале ${\mathcal {I}}$, определять $S_{x}=\{y\mid y{\text{ is between }}x{\text{ and }}c\}$. Для каждой точки y между x и c ,

$m(x)\leq {\frac {f(y)-f(x)}{g(y)-g(x)}}={\frac {{\frac {f(y)}{g(y)}}-{\frac {f(x)}{g(y)}}}{1-{\frac {g(x)}{g(y)}}}}\leq M(x).$

Когда y приближается к c , оба ${\frac {f(x)}{g(y)}}$ и ${\frac {g(x)}{g(y)}}$ станет нулем, и, следовательно,

$m(x)\leq \liminf _{y\in S_{x}}{\frac {f(y)}{g(y)}}\leq \limsup _{y\in S_{x}}{\frac {f(y)}{g(y)}}\leq M(x).$

Предел верхний и нижний предел необходимы, поскольку существование предела ⁠ ж / г ⁠ пока не установлена.

Это также тот случай, когда

$\lim _{x\to c}m(x)=\lim _{x\to c}M(x)=\lim _{x\to c}{\frac {f'(x)}{g'(x)}}=L.$

и

$\lim _{x\to c}\left(\liminf _{y\in S_{x}}{\frac {f(y)}{g(y)}}\right)=\liminf _{x\to c}{\frac {f(x)}{g(x)}}$ и $\lim _{x\to c}\left(\limsup _{y\in S_{x}}{\frac {f(y)}{g(y)}}\right)=\limsup _{x\to c}{\frac {f(x)}{g(x)}}.$

В случае 1 теорема о сжатии устанавливает, что $\lim _{x\to c}{\frac {f(x)}{g(x)}}$ существует и равен L . В случае 2 теорема о сжатии снова утверждает, что $\liminf _{x\to c}{\frac {f(x)}{g(x)}}=\limsup _{x\to c}{\frac {f(x)}{g(x)}}=L$, и поэтому предел $\lim _{x\to c}{\frac {f(x)}{g(x)}}$ существует и равен L . Это результат, который нужно было доказать.

предположение о том, что f ( x В случае 2 в доказательстве не использовалось ) стремится к бесконечности. Это означает, что если | г ( Икс )| расходится к бесконечности, когда x приближается к c и f и g удовлетворяют гипотезам правила Лопиталя, то никаких дополнительных предположений о пределе f ( x ) не требуется: может быть даже так, что предел f ( x ) не существует. В этом случае теорема Лопиталя на самом деле является следствием Чезаро-Штольца.

В случае, когда | г ( Икс )| расходится к бесконечности, когда x приближается к c и f ( x ) сходится к конечному пределу в c , то правило Лопиталя будет применимо, но не абсолютно необходимо, поскольку базовое предельное исчисление покажет, что предел f ( x )/ g ( x ) когда x приближается к c, должно быть равно нулю.

Следствие

Простое, но очень полезное следствие правила Лопиталя — известный критерий дифференцируемости. В нем говорится следующее: предположим, что f непрерывен в точке a и что $f'(x)$ существует для всех x в некотором открытом интервале, содержащем a , за исключением, возможно, $x=a$. Предположим, кроме того, что $\lim _{x\to a}f'(x)$ существует. Затем $f'(a)$ также существует и

$f'(a)=\lim _{x\to a}f'(x).$

В частности, f' также непрерывен в точке a .

Доказательство

Рассмотрим функции $h(x)=f(x)-f(a)$ и $g(x)=x-a$. Непрерывность f в a говорит нам, что $\lim _{x\to a}h(x)=0$. Более того, $\lim _{x\to a}g(x)=0$ поскольку полиномиальная функция всегда и везде непрерывна. Применение правила Лопиталя показывает, что $f'(a):=\lim _{x\to a}{\frac {f(x)-f(a)}{x-a}}=\lim _{x\to a}{\frac {h'(x)}{g'(x)}}=\lim _{x\to a}f'(x)$.

См. также

• Споры о больнице

Ссылки

Источники

• Чаттерджи, Дипак (2005), Реальный анализ , PHI Learning Pvt. ООО, ISBN  81-203-2678-4
• Кранц, Стивен Г. (2004), Справочник по действительным переменным. С приложениями к дифференциальным уравнениям и анализу Фурье , Бостон, Массачусетс: Birkhäuser Boston Inc., стр. xiv+201, doi : 10.1007/978-0-8176-8128-9 , ISBN  0-8176-4329-Х , МР   2015447
• Леттенмейер, Ф. (1936), «О так называемом больничном правиле», Журнал чистой и прикладной математики , 1936 (174): 246–247, doi : 10.1515/crll.1936.174.246 , S2CID   199546754
• Тейлор, А.Е. (1952), «Правило Лопиталя», амер. Математика. Monthly , 59 (1): 20–24, doi : 10.2307/2307183 , ISSN   0002-9890 , JSTOR   2307183 , MR   0044602.
• Важевски, Т. (1949), «Некоторые однородные демонстрации для всех случаев теоремы Госпиталя. Обобщения», Prace Mat.-Fiz. (на французском языке), 47 : 117–128, MR   0034430.