Штейнмец твердый

Твердое тело Штейнмеца (пересечение двух цилиндров)

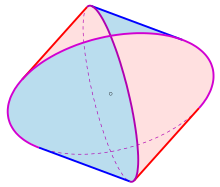
В геометрии называется телом Штейнмеца твердое тело, полученное в результате пересечения двух или трех цилиндров одинакового радиуса под прямым углом . Каждая из кривых пересечения двух цилиндров представляет собой эллипс.

Пересечение двух цилиндров называется бицилиндром . Топологически он эквивалентен квадратному осоэдру . Пересечение трех цилиндров называется трицилиндром . пополам бицилиндр Разрезанный называется сводом . и монастырский свод в архитектуре имеет именно такую ​​форму.

Тела Штейнмеца названы в честь математика Чарльза Протея Штейнмеца . который решил задачу определения объема перекрестка. Однако та же проблема была решена ранее Архимедом в древнегреческом мире. Цзу Чунчжи в древнем Китае. и Пьеро делла Франческа в раннем итальянском Возрождении. Они занимают видное место в скульптурах Фрэнка Смуллина .

Анимированное изображение велосипеда

Велосипединдер

Поколение велосипеда

Расчет объема бицилиндра

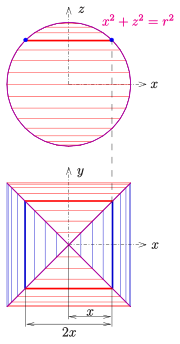
Бицилиндр, образованный двумя цилиндрами радиуса r, имеет объем

$$V={\frac {16}{3}}r^{3},$$

и площадь поверхности

$$A=16r^{2}.$$

Верхняя половина бицилиндра представляет собой квадратный корпус купольного свода , куполообразное тело, основанное на любом выпуклом многоугольнике, поперечное сечение которого представляет собой аналогичную копию многоугольника, и аналогичные формулы, вычисляющие объем и площадь поверхности купольного свода как в более общем плане справедливо рациональное кратное объему и площади поверхности охватывающей его призмы . В Китае велосипед известен как Моу хэ фанг гай , буквально «два квадратных зонтика»; его описал математик третьего века Лю Хуэй .

Доказательство формулы объема

Для вывода формулы объема удобно воспользоваться общепринятой идеей расчета объема сферы : собиранием тонких цилиндрических ломтиков. В данном случае тонкие ломтики представляют собой квадратные кубоиды (см. схему). Это приводит к

$${\begin{aligned}V&=\int _{-r}^{r}(2x)^{2}\ \mathrm {d} z\\[2pt]&=4\cdot \int _{-r}^{r}x^{2}\ \mathrm {d} z\\[2pt]&=4\cdot \int _{-r}^{r}(r^{2}-z^{2})\ \mathrm {d} z\\[2pt]&={\frac {16}{3}}r^{3}.\end{aligned}}$$

Известно , что отношения объемов прямого кругового конуса, половины сферы и прямого кругового цилиндра с одинаковыми радиусами и высотами равны 1:2:3 . Для половины бицилиндра справедливо аналогичное утверждение:

• Отношения объемов вписанной квадратной пирамиды $(a=2r,\ h=r,\ V={\tfrac {4}{3}}r^{3}),$ половина бицилиндра $(V={\tfrac {8}{3}}r^{3})$ и окружающий квадратный кубоид $(a=2r,\ h=r,\ V=4r^{3})$ 1 : 2 : 3 :
  $${\begin{array}{ccccc}{\frac {4}{3}}r^{3}&:&{\frac {8}{3}}r^{3}&:&4r^{3}\\[2pt]1&:&2&:&3\end{array}}$$

Использование многомерного исчисления

Рассмотрим уравнения цилиндров:

$${\begin{aligned}x^{2}+z^{2}&=r^{2}\\x^{2}+y^{2}&=r^{2}\end{aligned}}$$

Объем будет определяться:

$$V=\iiint _{V}\mathrm {d} z\,\mathrm {d} y\,\mathrm {d} x$$

С пределами интеграции:

$${\begin{array}{rcccl}-{\sqrt {r^{2}-x^{2}}}&\leqslant &z&\leqslant &{\sqrt {r^{2}-x^{2}}}\\[4pt]-{\sqrt {r^{2}-x^{2}}}&\leqslant &y&\leqslant &{\sqrt {r^{2}-x^{2}}}\\[4pt]-r&\leqslant &x&\leqslant &r\end{array}}$$

Подставив, имеем:

$${\begin{aligned}V&=\int _{-r}^{r}\int _{-{\sqrt {r^{2}-x^{2}}}}^{\sqrt {r^{2}-x^{2}}}\int _{-{\sqrt {r^{2}-x^{2}}}}^{\sqrt {r^{2}-x^{2}}}\mathrm {d} z\,\mathrm {d} y\,\mathrm {d} x\\[2pt]&=8r^{3}-{\frac {8r^{3}}{3}}\\[2pt]&={\frac {16r^{3}}{3}}\end{aligned}}$$

Доказательство формулы площади

Площадь поверхности состоит из двух красных и двух синих цилиндрических биугольников. Один красный биугольник разрезается пополам плоскостью yz и разворачивается в плоскость так, что полукруг (пересечение с плоскостью yz ) разворачивается на положительную ось ξ , а развертка двуугольника ограничивается вверх синусоидной дугой. $\eta =r\sin {\tfrac {\xi }{r}},\ 0\leq \xi \leq \pi r.$ Следовательно, область этого развития

монастырский свод

$$B=\int _{0}^{\pi r}r\sin {\frac {\xi }{r}}\ \mathrm {d} \xi =r^{2}\cos {0}-r^{2}\cos {\pi }=2r^{2}$$

а общая площадь поверхности равна:

$$A=8B=16r^{2}.$$

Альтернативное доказательство формулы объема

Вычислить объем бицилиндра (белого цвета) можно, упаковав его в куб (красного цвета). Плоскость (параллельная осям цилиндров), пересекающая бицилиндр, образует квадрат, а ее пересечение с кубом — квадрат большего размера. Разница площадей двух квадратов такая же, как у 4 маленьких квадратов (синего цвета). Когда плоскость движется через твердые тела, эти синие квадраты описывают квадратные пирамиды с равнобедренными гранями в углах куба; вершины пирамид находятся в середине четырех ребер куба. Перемещение плоскости по всему бицилиндру описывает всего 8 пирамид.

• 
  Метод Цзу Чунчжи (аналогичный принципу Кавальери ) расчета объема сферы включает в себя расчет объема бицилиндра.
• 
  Связь площади секции бицилиндра с секцией куба

Объем куба (красный) минус объем восьми пирамид (синий) равен объему бицилиндра (белый). Объем 8 пирамид равен:

$$8\times {\frac {1}{3}}r^{2}\times r={\frac {8}{3}}r^{3},$$

и тогда мы можем вычислить, что объем бицилиндра равен

$$(2r)^{3}-{\frac {8}{3}}r^{3}={\frac {16}{3}}r^{3}.$$

Трехцилиндровый

Создание поверхности трицилиндра: Сначала вырезаются два цилиндра (красный, синий). Созданный таким образом бицилиндр разрезается третьим (зеленым) цилиндром.

Пересечение трех цилиндров с перпендикулярно пересекающимися осями образует поверхность твердого тела с вершинами, в которых сходятся 3 ребра, и вершинами, в которых встречаются 4 ребра. Множество вершин можно рассматривать как ребра ромбододекаэдра . Ключом к определению объема и площади поверхности является наблюдение, что трицилиндр может быть преобразован в куб с вершинами, в которых сходятся 3 ребра (см. диаграмму) и 6 изогнутых пирамид (треугольники являются частями поверхностей цилиндра). Объем и площадь поверхности изогнутых треугольников могут быть определены из тех же соображений, что и для приведенного выше бицилиндра.

Объем трехцилиндрового цилиндра

$$V=8(2-{\sqrt {2}})r^{3}$$

а площадь поверхности

$$A=24(2-{\sqrt {2}})r^{2}.$$

Больше цилиндров

При четырех цилиндрах с осями, соединяющими вершины тетраэдра с соответствующими точками на другой стороне тела, объем равен

$$V_{4}=12\left(2{\sqrt {2}}-{\sqrt {6}}\right)r^{3}\,$$

Для шести цилиндров с осями, параллельными диагоналям граней куба , объём равен:

$$V_{6}={\frac {16}{3}}\left(3+2{\sqrt {3}}-4{\sqrt {2}}\right)r^{3}\,$$

См. также

• Копыта

Внешние ссылки

• 3D-модель твердого тела Штейнмеца в Google 3D Warehouse