Керл (математика)

В векторном исчислении ротор , также известный как ротор , представляет собой векторный оператор , описывающий бесконечно малую циркуляцию векторного поля в трехмерном евклидовом пространстве . Вихрь в точке поля представлен вектором, длина и направление которого обозначают величину и ось максимальной циркуляции. ^[1] Ротор поля формально определяется как плотность циркуляции в каждой точке поля.

Векторное поле, ротор которого равен нулю, называется безвихревым . Ротор — это форма дифференцирования векторных полей. Соответствующей формой фундаментальной теоремы исчисления является теорема Стокса , которая связывает поверхностный интеграл ротора векторного поля с линейным интегралом векторного поля вокруг граничной кривой.

Обозначение $локон F$ более распространено в Северной Америке. В остальном мире, особенно в научной литературе 20-го века, традиционно используется альтернативное обозначение $rot F$ , которое происходит от «скорости вращения», которую оно представляет. Чтобы избежать путаницы, современные авторы склонны использовать обозначение векторного произведения с оператором del (набла), как в $\nabla \times \mathbf {F}$ , ^[2] что также раскрывает связь между операторами ротора (ротора), дивергенции и градиента .

В отличие от градиента и дивергенции , ротор, сформулированный в векторном исчислении, не распространяется просто на другие измерения; возможны некоторые обобщения , но только в трех измерениях геометрически определенный ротор векторного поля снова является векторным полем. Этот недостаток является прямым следствием ограничений векторного исчисления; с другой стороны, когда выражается как антисимметричное тензорное поле через оператор клина геометрического исчисления , ротор обобщается на все измерения. Обстоятельство аналогично тому, что имеет место при 3-мерном векторном произведении , и действительно связь отражена в обозначениях $\nabla \times$ для завитка.

Название «завиток» впервые предложил Джеймс Клерк Максвелл в 1871 году. ^[3] при построении теории оптического поля но эта концепция, по-видимому, впервые была использована Джеймсом МакКаллагом в 1839 году. ^[4]^[5]

Определение [ править ]

Компоненты

F

в положении

r

, нормальные и касательные к замкнутой кривой

C

на плоскости, охватывающей область плоского вектора .

\mathbf {A} =A\mathbf {\hat {n}}

.

Правило правой руки

Соглашение о векторной ориентации линейного интеграла

Большой палец указывает в направлении

\mathbf {\hat {n}}

и пальцы сгибаются в направлении

C

Ротор векторного поля $F$ , обозначаемый $ротором F$ , или $\nabla \times \mathbf {F}$ или $rot F$ — оператор, отображающий $C к$ функции в $R 3$ до $С к -1$ функции в $R 3$ , и, в частности, отображает непрерывно дифференцируемые функции $R 3 \to Р 3$ к непрерывным функциям $R 3 \to Р 3$ . Его можно определить несколькими способами, которые будут упомянуты ниже:

Один из способов определить ротор векторного поля в точке — неявно через его компоненты вдоль различных осей, проходящих через точку: если $\mathbf {\hat {u}}$ - любой единичный вектор, компонент ротора $F$ в направлении $\mathbf {\hat {u}}$ можно определить как предельное значение интеграла по замкнутой линии в плоскости, перпендикулярной $\mathbf {\hat {u}}$ делится на охватываемую площадь, поскольку путь интегрирования бесконечно сжимается вокруг точки.

Более конкретно, ротор определяется в точке $p$ как ^[6]^[7]

(\nabla \times \mathbf {F} )(p)\cdot \mathbf {\hat {u}} \ {\overset {\underset {\mathrm {def} }{}}{{}={}}}\lim _{A\to 0}{\frac {1}{|A|}}\oint _{C}\mathbf {F} \cdot \mathrm {d} \mathbf {r}

где линейный интеграл вычисляется вдоль границы

C

области A

,

рассматриваемой

| А |

является величиной площади. Это уравнение определяет компоненту ротора

F

вдоль направления

\mathbf {\hat {u}}

. Инфинитезимальные поверхности, ограниченные

C

, имеют

\mathbf {\hat {u}}

как обычно .

C

ориентирован по правилу правой руки .

Приведенная выше формула означает, что составляющая ротора векторного поля вдоль определенной оси представляет собой бесконечно малую плотность площади циркуляции поля в плоскости, перпендикулярной этой оси. не Эта формула априори определяет законного векторного поля, поскольку отдельные плотности циркуляции по отношению к различным осям априори не обязательно должны относиться друг к другу так же, как компоненты вектора; то, что они действительно относятся друг к другу именно таким образом, должно быть доказано отдельно.

К этому определению естественным образом подходит теорема Кельвина–Стокса как глобальная формула, соответствующая определению. Он приравнивает поверхностный интеграл ротора векторного поля к указанному выше линейному интегралу, взятому вокруг границы поверхности.

Другой способ определить вектор ротора функции $F$ в точке - это явное значение векторного поверхностного интеграла вокруг оболочки, охватывающей $p$ , деленное на объем, заключенный в ней, поскольку оболочка бесконечно сжимается вокруг $p$ .

Более конкретно, ротор может быть определен векторной формулой

(\nabla \times \mathbf {F} )(p){\overset {\underset {\mathrm {def} }{}}{{}={}}}\lim _{V\to 0}{\frac {1}{|V|}}\oint _{S}\mathbf {\hat {n}} \times \mathbf {F} \ \mathrm {d} S

где поверхностный интеграл вычисляется вдоль границы

S

объема

V

,

| В |

являющийся величиной объема, и

\mathbf {\hat {n}}

направленный наружу от поверхности

S

перпендикулярно в каждой точке

S

.

В этой формуле векторное произведение в подынтегральном выражении измеряет тангенциальную составляющую $F$ поверхности $S$ и указывает вдоль поверхности под прямым углом к тангенциальной проекции F $в каждой точке$ . Интегрирование этого векторного произведения по всей поверхности дает вектор, величина которого измеряет общую циркуляцию $F$ вокруг $S$ и направление которой перпендикулярно этой циркуляции. Приведенная выше формула говорит, что ротор векторного поля в точке — это бесконечно малая объемная плотность этого «вектора циркуляции» вокруг точки.

К этому определению естественным образом подходит другая глобальная формула (аналогичная теореме Кельвина-Стокса), которая приравнивает объемный интеграл ротора векторного поля к вышеуказанному поверхностному интегралу, взятому по границе объема.

В то время как два приведенных выше определения ротора не содержат координат, существует еще одно «легкое для запоминания» определение ротора в криволинейных ортогональных координатах , например, в декартовых , сферических , цилиндрических или даже эллиптических или параболических координатах :

{\begin{aligned}&(\operatorname {curl} \mathbf {F} )_{1}={\frac {1}{h_{2}h_{3}}}\left({\frac {\partial (h_{3}F_{3})}{\partial u_{2}}}-{\frac {\partial (h_{2}F_{2})}{\partial u_{3}}}\right),\\[5pt]&(\operatorname {curl} \mathbf {F} )_{2}={\frac {1}{h_{3}h_{1}}}\left({\frac {\partial (h_{1}F_{1})}{\partial u_{3}}}-{\frac {\partial (h_{3}F_{3})}{\partial u_{1}}}\right),\\[5pt]&(\operatorname {curl} \mathbf {F} )_{3}={\frac {1}{h_{1}h_{2}}}\left({\frac {\partial (h_{2}F_{2})}{\partial u_{1}}}-{\frac {\partial (h_{1}F_{1})}{\partial u_{2}}}\right).\end{aligned}}

Уравнение для каждого компонента $(curl F) k$ можно получить путем замены каждого вхождения индекса 1, 2, 3 в циклической перестановке: 1 → 2, 2 → 3 и 3 → 1 (где индексы представляют соответствующие индексы). .

Если $(x 1, x 2, x 3)$ являются декартовыми координатами и $(u 1, u 2, u 3)$ являются ортогональными координатами, то

h_{i}={\sqrt {\left({\frac {\partial x_{1}}{\partial u_{i}}}\right)^{2}+\left({\frac {\partial x_{2}}{\partial u_{i}}}\right)^{2}+\left({\frac {\partial x_{3}}{\partial u_{i}}}\right)^{2}}}

длина координатного вектора, соответствующего

u i

. Остальные два компонента ротора являются результатом перестановки индексов циклической : 3,1,2 → 1,2,3 → 2,3,1.

Использование [ править ]

На практике два бескоординатных определения, описанные выше, используются редко, поскольку практически во всех случаях оператор завитка может быть применен с использованием некоторого набора криволинейных координат , для которых были получены более простые представления.

Обозначение $\nabla \times F$ берет свое начало от сходства с трехмерным векторным произведением и полезно в качестве мнемоники в декартовых координатах, если $\nabla$ берется как векторный дифференциальный оператор del . Такие обозначения с участием операторов распространены в физике и алгебре .

Развернутое в трехмерных декартовых координатах (см. Del в цилиндрических и сферических координатах для сферических и цилиндрических координатных представлений), $\nabla \times F$ представляет собой $F$ , состоящее из $[F x, F y, F z]$ (где нижние индексы указывают компоненты вектор, а не частные производные):

\nabla \times \mathbf {F} ={\begin{vmatrix}{\boldsymbol {\hat {\imath }}}&{\boldsymbol {\hat {\jmath }}}&{\boldsymbol {\hat {k}}}\\[5mu]{\dfrac {\partial }{\partial x}}&{\dfrac {\partial }{\partial y}}&{\dfrac {\partial }{\partial z}}\\[5mu]F_{x}&F_{y}&F_{z}\end{vmatrix}}

где

i

,

j

и

k

— единичные векторы для осей

x

,

y

и

z

соответственно. Это расширяется следующим образом: ^[8]

\nabla \times \mathbf {F} =\left({\frac {\partial F_{z}}{\partial y}}-{\frac {\partial F_{y}}{\partial z}}\right){\boldsymbol {\hat {\imath }}}+\left({\frac {\partial F_{x}}{\partial z}}-{\frac {\partial F_{z}}{\partial x}}\right){\boldsymbol {\hat {\jmath }}}+\left({\frac {\partial F_{y}}{\partial x}}-{\frac {\partial F_{x}}{\partial y}}\right){\boldsymbol {\hat {k}}}

Хотя результат и выражен в координатах, он инвариантен при правильном вращении координатных осей, но результат инвертируется при отражении.

В общей системе координат ротор определяется выражением ^[1]

(\nabla \times \mathbf {F} )^{k}={\frac {1}{\sqrt {g}}}\varepsilon ^{k\ell m}\nabla _{\ell }F_{m}

где

ε

обозначает тензор Леви-Чивита ,

\nabla

ковариантную производную ,

g

является определителем метрического тензора , а соглашение Эйнштейна о суммировании подразумевает, что повторяющиеся индексы суммируются. Благодаря симметрии символов Кристоффеля, участвующих в ковариантной производной, это выражение сводится к частной производной:

(\nabla \times \mathbf {F} )={\frac {1}{\sqrt {g}}}\mathbf {R} _{k}\varepsilon ^{k\ell m}\partial _{\ell }F_{m}

где

R k

— локальные базисные векторы. Эквивалентно, используя внешнюю производную , ротор можно выразить как:

\nabla \times \mathbf {F} =\left(\star {\big (}{\mathrm {d} }\mathbf {F} ^{\flat }{\big )}\right)^{\sharp }

Здесь ♭ и ♯ — музыкальные изоморфизмы , а $★$ — оператор звезды Ходжа . Эта формула показывает, как вычислить ротор $F$ в любой системе координат и как распространить ротор на любое ориентированное трехмерное риманово многообразие. Поскольку это зависит от выбора ориентации, завиток является киральной операцией. Другими словами, если ориентация меняется на противоположную, то и направление завитка меняется на противоположное.

Примеры [ править ]

Пример 1 [ править ]

Предположим, что векторное поле описывает поле скоростей ( потока жидкости например, большого резервуара с жидкостью или газом ), а внутри жидкости или газа находится небольшой шарик (центр шара зафиксирован в определенной точке). Если поверхность шара шероховатая, протекающая мимо него жидкость заставит его вращаться. Ось вращения (ориентированная по правилу правой руки) указывает в сторону завитка поля в центре шара, а угловая скорость вращения равна половине величины завитка в этой точке. ^[9]Ротор векторного поля в любой точке задается вращением бесконечно малой области в плоскости xy (для z компонента ротора по оси ), плоскости zx (для y компонента ротора по оси ) и yz - плоскость (для компоненты оси x вектора ротора). Это можно увидеть на примерах ниже.

Пример 2 [ править ]

Векторное поле

F (x, y)=[y,- x]

(слева) и его ротор (справа).

Векторное поле

\mathbf {F} (x,y,z)=y{\boldsymbol {\hat {\imath }}}-x{\boldsymbol {\hat {\jmath }}}

можно разложить как

F_{x}=y,F_{y}=-x,F_{z}=0.

При визуальном осмотре поле можно охарактеризовать как «вращающееся». Если бы векторы поля представляли линейную силу , действующую на объекты, присутствующие в этой точке, и объект должен был быть помещен внутри поля, объект начал бы вращаться вокруг себя по часовой стрелке. Это справедливо независимо от того, где находится объект.

Расчет завитка:

\nabla \times \mathbf {F} =0{\boldsymbol {\hat {\imath }}}+0{\boldsymbol {\hat {\jmath }}}+\left({\frac {\partial }{\partial x}}(-x)-{\frac {\partial }{\partial y}}y\right){\boldsymbol {\hat {k}}}=-2{\boldsymbol {\hat {k}}}

Результирующее векторное поле, описывающее завиток, во всех точках будет указывать в отрицательном $направлении z$ . Результаты этого уравнения совпадают с тем, что можно было бы предсказать с помощью правила правой руки и правосторонней системы координат . Будучи однородным векторным полем, описанный выше объект будет иметь одинаковую интенсивность вращения независимо от того, где он находится.

Пример 3 [ править ]

Векторное поле

F (x, y) = [0, - x 2]

(слева) и его завиток (справа).

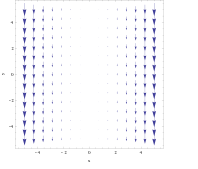
Для векторного поля

\mathbf {F} (x,y,z)=-x^{2}{\boldsymbol {\hat {\jmath }}}

изгиб не так очевиден на графике. Однако если взять объект из предыдущего примера и поместить его в любое место на линии $x = 3$ , сила, действующая с правой стороны, будет немного больше, чем сила, действующая с левой, что заставит его вращаться по часовой стрелке. Используя правило правой руки, можно предсказать, что результирующий завиток будет прямым в отрицательном $направлении z$ . И наоборот, если объект поместить на $x = -3$ , объект будет вращаться против часовой стрелки, и правило правой руки приведет к положительному $направлению z$ .

Расчет завитка:

{\nabla }\times \mathbf {F} =0{\boldsymbol {\hat {\imath }}}+0{\boldsymbol {\hat {\jmath }}}+{\frac {\partial }{\partial x}}\left(-x^{2}\right){\boldsymbol {\hat {k}}}=-2x{\boldsymbol {\hat {k}}}.

Завиток указывает в отрицательном $направлении z$ , когда $x$ положителен, и наоборот. В этом поле интенсивность вращения будет тем больше, чем объект удаляется от плоскости $x = 0$ .

Дальнейшие примеры [ править ]

В векторном поле, описывающем линейные скорости каждой части вращающегося диска, находящегося в равномерном круговом движении , ротор имеет одинаковое значение во всех точках, и это значение оказывается ровно в два раза больше векторной угловой скорости диска (ориентированной как обычно по правилу правой руки ). В более общем смысле, для любой текущей массы векторное поле линейной скорости в каждой точке массового потока имеет ротор (завихренность потока в этой точке), равный ровно в два раза локальной векторной угловой скорости массы вокруг этой точки.
Для любого твердого объекта, на который действует внешняя физическая сила (например, гравитация или электромагнитная сила), можно рассмотреть векторное поле, представляющее бесконечно малые вклады силы на единицу объема, действующие в каждой из точек объекта. Это силовое поле может создать чистый крутящий момент объекта вокруг его центра масс, и этот крутящий момент оказывается прямо пропорциональным и векторно параллельным (векторному) интегралу от ротора силового поля по всему объему.
Из четырех уравнений Максвелла два — закон Фарадея и закон Ампера — можно компактно выразить с помощью ротора. Закон Фарадея утверждает, что ротор электрического поля равен обратному значению скорости изменения магнитного поля во времени, а закон Ампера связывает ротор магнитного поля с током и скоростью изменения электрического поля во времени.

Личности [ править ]

В общих криволинейных координатах , что ротор векторного произведения векторных полей $v$ и $F$ (не только в декартовых координатах) можно показать равен

\nabla \times \left(\mathbf {v\times F} \right)={\Big (}\left(\mathbf {\nabla \cdot F} \right)+\mathbf {F\cdot \nabla } {\Big )}\mathbf {v} -{\Big (}\left(\mathbf {\nabla \cdot v} \right)+\mathbf {v\cdot \nabla } {\Big )}\mathbf {F} \ .

Поменяв местами векторное поле $v$ и $оператор \nabla$ , мы приходим к векторному произведению векторного поля на ротор векторного поля:

\mathbf {v\ \times } \left(\mathbf {\nabla \times F} \right)=\nabla _{\mathbf {F} }\left(\mathbf {v\cdot F} \right)-\left(\mathbf {v\cdot \nabla } \right)\mathbf {F} \ ,

где

\nabla F

— индекс Фейнмана, который учитывает только изменение, вызванное векторным полем

F

(т. е. в этом случае

v

считается постоянным в пространстве).

Другой пример — ротор ротора векторного поля. Можно показать, что в общих координатах

\nabla \times \left(\mathbf {\nabla \times F} \right)=\mathbf {\nabla } (\mathbf {\nabla \cdot F} )-\nabla ^{2}\mathbf {F} \ ,

и это тождество определяет векторный лапласиан F

,

обозначенный как

\nabla 2 Ф.

Ротор градиента любого скалярного . поля $φ$ всегда является нулевым векторным полем

\nabla \times (\nabla \varphi )={\boldsymbol {0}}

что следует из антисимметрии в определении ротора и симметрии вторых производных .

Дивергенция ротора любого векторного поля равна нулю:

\nabla \cdot (\nabla \times \mathbf {F} )=0.

Если $φ$ — скалярная функция, а $F$ — векторное поле, то

\nabla \times (\varphi \mathbf {F} )=\nabla \varphi \times \mathbf {F} +\varphi \nabla \times \mathbf {F}

Обобщения [ править ]

Операции векторного исчисления grad , curl и div легче всего обобщаются в контексте дифференциальных форм, что включает в себя ряд шагов. Короче говоря, они соответствуют производным 0-форм, 1-форм и 2-форм соответственно. Геометрическая интерпретация ротора как вращения соответствует отождествлению бивекторов (2-векторов) в трех измерениях со специальной ортогональной алгеброй Ли. ${\mathfrak {so}}(3)$ бесконечно малых вращений (в координатах — кососимметричные матрицы 3 × 3), а представление вращений векторами соответствует идентификации 1-векторов (эквивалентно 2-векторам) и ${\mathfrak {so}}(3)$ , все это трехмерные пространства.

Дифференциальные формы [ править ]

В трех измерениях дифференциальная 0-форма представляет собой вещественную функцию $f (x, y, z)$ ; дифференциальная 1-форма — это следующее выражение, где коэффициенты являются функциями:

a_{1}\,dx+a_{2}\,dy+a_{3}\,dz;

дифференциальная 2-форма - это формальная сумма, опять же с функциональными коэффициентами:

a_{12}\,dx\wedge dy+a_{13}\,dx\wedge dz+a_{23}\,dy\wedge dz;

а дифференциальная 3-форма определяется одним членом с одной функцией в качестве коэффициента:

a_{123}\,dx\wedge dy\wedge dz.

(Здесь

a -коэффициенты

являются действительными функциями трех переменных; «клиновые произведения», например

dx \land dy

, можно интерпретировать как своего рода ориентированные элементы площади,

dx \land dy = - dy \land dx

и т. д.)

Внешняя производная k $-формы$ в $R 3$ определяется как $(k + 1)$ -форма сверху, а в $R н$ если, например,

\omega ^{(k)}=\sum _{1\leq i_{1}<i_{2}<\cdots <i_{k}\leq n}a_{i_{1},\ldots ,i_{k}}\,dx_{i_{1}}\wedge \cdots \wedge dx_{i_{k}},

тогда внешняя производная

d

приводит к

d\omega ^{(k)}=\sum _{\scriptstyle {j=1} \atop \scriptstyle {i_{1}<\cdots <i_{k}}}^{n}{\frac {\partial a_{i_{1},\ldots ,i_{k}}}{\partial x_{j}}}\,dx_{j}\wedge dx_{i_{1}}\wedge \cdots \wedge dx_{i_{k}}.

Таким образом, внешняя производная 1-формы является 2-формой, а 2-формы — 3-формой. С другой стороны, из-за взаимозаменяемости смешанных производных инструментов

{\frac {\partial ^{2}}{\partial x_{i}\,\partial x_{j}}}={\frac {\partial ^{2}}{\partial x_{j}\,\partial x_{i}}},

и антисимметрия,

dx_{i}\wedge dx_{j}=-dx_{j}\wedge x_{i}

двойное применение внешней производной дает $0$ (ноль $k+2$ -форма).

Таким образом, обозначая пространство $k$ -форм через $Ω к (Р 3)$ и внешней производной по $d$ получается последовательность:

0\,{\overset {d}{\longrightarrow }}\;\Omega ^{0}\left(\mathbb {R} ^{3}\right)\,{\overset {d}{\longrightarrow }}\;\Omega ^{1}\left(\mathbb {R} ^{3}\right)\,{\overset {d}{\longrightarrow }}\;\Omega ^{2}\left(\mathbb {R} ^{3}\right)\,{\overset {d}{\longrightarrow }}\;\Omega ^{3}\left(\mathbb {R} ^{3}\right)\,{\overset {d}{\longrightarrow }}\,0.

Здесь $Ом к (Р н)$ — пространство сечений внешней алгебры $Λ к (Р н)$ векторное расслоение над R ^н, размерность которого представляет собой биномиальный коэффициент $(н к)$ ; отметим, что $Ω к (Р 3) = 0$ для $k > 3$ или $k < 0$ . Записав только размеры, получим ряд треугольника Паскаля :

0 → 1 → 3 → 3 → 1 → 0;

одномерные слои соответствуют скалярным полям, а трехмерные — векторным полям, как описано ниже. По модулю подходящих отождествлений три нетривиальных вхождения внешней производной соответствуют grad, curl и div.

Дифференциальные формы и дифференциал могут быть определены в любом евклидовом пространстве или даже в любом многообразии без какого-либо понятия римановой метрики. На римановом многообразии или, в более общем смысле , псевдоримановом многообразии , $k-$ формы могут быть отождествлены с $k$ -векторными полями ( $k$ -формы — это $k$ -ковекторные поля, а псевдориманова метрика дает изоморфизм между векторами и ковекторами), и в ориентированном векторном пространстве невырожденной формы (изоморфизм между векторами и ковекторами) существует изоморфизм между $k$ -векторами и $(n - k)$ -векторами; в частности, на (касательном пространстве) ориентированного псевдориманова многообразия. Таким образом, на ориентированном псевдоримановом многообразии можно менять местами $k$ -формы, $k$ -векторные поля, $(n - k)$ -формы и $(n - k)$ -векторные поля; это известно как двойственность Ходжа . Конкретно на $Р 3$ это дано:

1-формы и 1-векторные поля: 1-форма $a x dx + a y dy + a z dz$ соответствует векторному полю $(a x, a y, a z)$ .
1-формы и 2-формы: $dx$ заменяют двойственной величиной $dy \land dz$ (т. е. опускают $dx$ ), а также, учитывая ориентацию: $dy$ соответствует $dz \land dx = - dx \land dz$ , а $dz$ соответствует $dx \land ды$ . Таким образом, форма $a x dx + a y dy + a z dz$ соответствует «двойственной форме» $a z dx \land dy + a y dz \land dx + a x dy \land dz$ .

Таким образом, отождествляя 0-формы и 3-формы со скалярными полями, а 1-формы и 2-формы с векторными полями:

grad переводит скалярное поле (0-форму) в векторное поле (1-форму);
Curl переводит векторное поле (1-форму) в псевдовекторное поле (2-форму);
div преобразует псевдовекторное поле (2-форму) в псевдоскалярное поле (3-форму)

С другой стороны, тот факт, что $д 2 = 0$ соответствует тождествам

\nabla \times (\nabla f)=\mathbf {0}

для любого скалярного поля

f

и

\nabla \cdot (\nabla \times \mathbf {v} )=0

для любого векторного поля

v

.

Grad и div обобщаются на все ориентированные псевдоримановы многообразия с той же геометрической интерпретацией, поскольку пространства 0-форм и $n$ -форм в каждой точке всегда одномерны и могут быть отождествлены со скалярными полями, а пространства 1-мерных -формы и $(n - 1)$ -формы всегда послойно $n$ -мерны и могут быть отождествлены с векторными полями.

Curl не обобщает таким образом до 4 или более измерений (или до 2 или менее измерений); в 4 измерениях размеры

0 → 1 → 4 → 6 → 4 → 1 → 0;

поэтому ротор 1-векторного поля (послойно 4-мерного) представляет собой 2-векторное поле , которое в каждой точке принадлежит 6-мерному векторному пространству, и поэтому имеем

\omega ^{(2)}=\sum _{i<k=1,2,3,4}a_{i,k}\,dx_{i}\wedge dx_{k},

что дает сумму шести независимых членов и не может быть отождествлено с 1-векторным полем. Также невозможно осмысленно перейти от 1-векторного поля к 2-векторному полю и к 3-векторному полю (4 → 6 → 4), поскольку двукратное взятие дифференциала дает ноль (

d 2 = 0

). Таким образом, таким образом не возникает никакой функции ротора от векторных полей к векторным полям в других измерениях.

Однако можно определить ротор векторного поля как 2-векторное поле в целом, как описано ниже.

Завить геометрически [ править ]

2-векторы соответствуют внешней степени $Λ 2 В$ ; при наличии скалярного произведения в координатах это кососимметричные матрицы, геометрически рассматриваемые как специальная ортогональная алгебра Ли ${\mathfrak {so}}$ бесконечно малых вращений. Это имеет $( н 2 ) = .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}1/2 n измерений − ( n 1)$ и позволяет интерпретировать дифференциал 1-векторного поля как его бесконечно малые вращения. Только в 3-х измерениях (или тривиально в 0-х измерениях) мы имеем $n = 1/2 ., n (n - 1)$ что является наиболее элегантным и распространенным случаем В двумерном измерении ротор векторного поля - это не векторное поле, а функция, поскольку двумерное вращение задается углом (скаляр - ориентация требуется, чтобы выбрать, считать ли вращение по часовой стрелке или против часовой стрелки положительным); это не div, а скорее перпендикулярно ему. В трехмерном измерении ротор векторного поля является, как известно, векторным полем (в одномерном и нулевом измерениях ротор векторного поля равен 0, поскольку не существует нетривиальных 2-векторов), а в четырехмерном ротор векторное поле геометрически в каждой точке является элементом 6-мерной алгебры Ли. ${\mathfrak {so}}(4)$ .

Ротор трехмерного векторного поля, которое зависит только от двух координат (скажем, $x$ и $y$ ), представляет собой просто вертикальное векторное поле (в $направлении z$ ), величина которого равна ротору двумерного векторного поля, как в примерах. на этой странице.

Рассмотрение ротора как 2-векторного поля (антисимметричного 2-тензора) использовалось для обобщения векторного исчисления и связанной с ним физики на более высокие измерения. ^[10]

Инверсия [ править ]

В случае, когда дивергенция векторного поля $V$ равна нулю, векторное поле $W$ существует такое, что $V = ротор(W)$ . ^{[ нужна цитата ]} Вот почему магнитное поле , характеризующееся нулевой дивергенцией, можно выразить как ротор магнитного векторного потенциала .

Если $W$ векторное поле с $curl(W) = V$ , то добавление любого градиентного векторного поля $grad(f)$ к $W$ приведет к другому векторному полю $W + grad(f)$ такому, что $curl(W + grad(f)) = В$ тоже. Это можно резюмировать, сказав, что обратный ротор трехмерного векторного поля можно получить с точностью до неизвестного безвихревого поля с помощью закона Био – Савара .

См. также [ править ]

Ссылки [ править ]

^ Перейти обратно: ^а ^б Вайсштейн, Эрик В. «Кёрл» . Математический мир .
^ Стандарт ISO/IEC 80000-2 Норма ISO/IEC 80000-2, пункт 2-17.16
^ Труды Лондонского математического общества, 9 марта 1871 г.
^ Собрание сочинений Джеймса МакКалла . Дублин: Ходжес. 1880.
^ Самые ранние известные варианты использования некоторых математических слов tripod.com
^ Математические методы в физике и технике, К. Ф. Райли, М. П. Хобсон, С. Дж. Бенс, Cambridge University Press, 2010, ISBN 978-0-521-86153-3
^ Векторный анализ (2-е издание), М. Р. Шпигель, С. Липшуц, Д. Спеллман, Очерки Шаума, McGraw Hill (США), 2009 г., ISBN 978-0-07-161545-7
^ Арфкен, Джордж Браун (2005). Математические методы для физиков . Вебер, Ханс-Юрген (6-е изд.). Бостон: Эльзевир. п. 43. ИСБН 978-0-08-047069-6 . OCLC 127114279 .
^ Гиббс, Джозайя Уиллард ; Уилсон, Эдвин Бидвелл (1901), Векторный анализ , Публикации к двухсотлетию Йельского университета, Сыновья К. Скрибнера, hdl : 2027/mdp.39015000962285
^ Макдэвид, AW; Макмаллен, компакт-диск (30 октября 2006 г.). «Обобщение перекрестных произведений и уравнений Максвелла на универсальные дополнительные измерения». arXiv : hep-ph/0609260 .

Дальнейшее чтение [ править ]

Корн, Гранино Артур и Тереза М. Корн (январь 2000 г.). Математический справочник для ученых и инженеров: определения, теоремы и формулы для справки и обзора . Нью-Йорк: Dover Publications. стр. 157–160. ISBN 0-486-41147-8 .
Шей, Х.М. (1997). Div, Grad, Curl и все такое: неформальный текст по векторному исчислению . Нью-Йорк: Нортон. ISBN 0-393-96997-5 .

Внешние ссылки [ править ]

«Завиток» , Математическая энциклопедия , EMS Press , 2001 [1994]
«Многомерное исчисление» . mathinsight.org . Проверено 12 февраля 2022 г.
«Дивергенция и завиток: язык уравнений Максвелла, поток жидкости и многое другое» . 21 июня 2018 г. Архивировано из оригинала 24 ноября 2021 г. – на YouTube .

[Mathworld-1] Перейти обратно: ^а ^б Вайсштейн, Эрик В. «Кёрл» . Математический мир .

[2] Стандарт ISO/IEC 80000-2 Норма ISO/IEC 80000-2, пункт 2-17.16

[3] Труды Лондонского математического общества, 9 марта 1871 г.

[4] Собрание сочинений Джеймса МакКалла . Дублин: Ходжес. 1880.

[5] Самые ранние известные варианты использования некоторых математических слов tripod.com

[6] Математические методы в физике и технике, К. Ф. Райли, М. П. Хобсон, С. Дж. Бенс, Cambridge University Press, 2010, ISBN 978-0-521-86153-3

[7] Векторный анализ (2-е издание), М. Р. Шпигель, С. Липшуц, Д. Спеллман, Очерки Шаума, McGraw Hill (США), 2009 г., ISBN 978-0-07-161545-7

[8] Арфкен, Джордж Браун (2005). Математические методы для физиков . Вебер, Ханс-Юрген (6-е изд.). Бостон: Эльзевир. п. 43. ИСБН 978-0-08-047069-6 . OCLC 127114279 .

[9] Гиббс, Джозайя Уиллард ; Уилсон, Эдвин Бидвелл (1901), Векторный анализ , Публикации к двухсотлетию Йельского университета, Сыновья К. Скрибнера, hdl : 2027/mdp.39015000962285

[10] Макдэвид, AW; Макмаллен, компакт-диск (30 октября 2006 г.). «Обобщение перекрестных произведений и уравнений Максвелла на универсальные дополнительные измерения». arXiv : hep-ph/0609260 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

v т Это Исчисление
Precalculus	Binomial theorem Concave function Continuous function Factorial Finite difference Free variables and bound variables Graph of a function Linear function Radian Rolle's theorem Secant Slope Tangent
Limits	Indeterminate form Limit of a function One-sided limit Limit of a sequence Order of approximation (ε, δ)-definition of limit
Differential calculus	Derivative Second derivative Partial derivative Differential Differential operator Mean value theorem Notation Leibniz's notation Newton's notation Rules of differentiation linearity Power Sum Chain L'Hôpital's Product General Leibniz's rule Quotient Other techniques Implicit differentiation Inverse functions and differentiation Logarithmic derivative Related rates Stationary points First derivative test Second derivative test Extreme value theorem Maximum and minimum Further applications Newton's method Taylor's theorem Differential equation Ordinary differential equation Partial differential equation Stochastic differential equation
Integral calculus	Antiderivative Arc length Riemann integral Basic properties Constant of integration Fundamental theorem of calculus Differentiating under the integral sign Integration by parts Integration by substitution trigonometric Euler Tangent half-angle substitution Partial fractions in integration Quadratic integral Trapezoidal rule Volumes Washer method Shell method Integral equation Integro-differential equation
Vector calculus	Derivatives Curl Directional derivative Divergence Gradient Laplacian Basic theorems Line integrals Green's Stokes' Gauss'
Multivariable calculus	Divergence theorem Geometric Hessian matrix Jacobian matrix and determinant Lagrange multiplier Line integral Matrix Multiple integral Partial derivative Surface integral Volume integral Advanced topics Differential forms Exterior derivative Generalized Stokes' theorem Tensor calculus
Sequences and series	Arithmetico-geometric sequence Types of series Alternating Binomial Fourier Geometric Harmonic Infinite Power Maclaurin Taylor Telescoping Tests of convergence Abel's Alternating series Cauchy condensation Direct comparison Dirichlet's Integral Limit comparison Ratio Root Term
Special functions and numbers	Bernoulli numbers e (mathematical constant) Exponential function Natural logarithm Stirling's approximation
History of calculus	Adequality Brook Taylor Colin Maclaurin Generality of algebra Gottfried Wilhelm Leibniz Infinitesimal Infinitesimal calculus Isaac Newton Fluxion Law of Continuity Leonhard Euler Method of Fluxions The Method of Mechanical Theorems
Lists	Differentiation rules List of integrals of exponential functions List of integrals of hyperbolic functions List of integrals of inverse hyperbolic functions List of integrals of inverse trigonometric functions List of integrals of irrational functions List of integrals of logarithmic functions List of integrals of rational functions List of integrals of trigonometric functions Secant Secant cubed List of limits Lists of integrals
Miscellaneous topics	Complex calculus Contour integral Differential geometry Manifold Curvature of curves of surfaces Tensor Euler–Maclaurin formula Gabriel's horn Integration Bee Proof that 22/7 exceeds π Regiomontanus' angle maximization problem Steinmetz solid