Дифференциал функции

Чтобы узнать о других значениях слова «дифференциал» в математике, см. «Дифференциал (математика)» .

В исчислении дифференциал . представляет собой основную часть изменения функции $y=f(x)$относительно изменений независимой переменной. Дифференциал $dy$ определяется

$$dy=f'(x)\,dx,$$

где $f'(x)$ является производной f ​ по $x$, и $dx$ является дополнительной действительной переменной (так что $dy$ является функцией $x$ и $dx$). Обозначения таковы, что уравнение

$$dy={\frac {dy}{dx}}\,dx$$

имеет место, где производная представлена ​​в обозначениях Лейбница $dy/dx$, и это согласуется с представлением о производной как о частном дифференциалов. Еще один пишет

$$df(x)=f'(x)\,dx.$$

Точное значение переменных $dy$ и $dx$зависит от контекста приложения и требуемого уровня математической строгости. Область определения этих переменных может иметь особое геометрическое значение, если дифференциал рассматривается как особая дифференциальная форма , или аналитическое значение, если дифференциал рассматривается как линейное приближение к приращению функции. Традиционно переменные $dx$ и $dy$ считаются очень малыми ( бесконечно малыми ), и эта интерпретация становится строгой в нестандартном анализе .

История и использование

Дифференциал был впервые введен через интуитивное или эвристическое определение Исааком Ньютоном и развит Готфридом Лейбницем , который думал о дифференциале dy как о бесконечно малом (или бесконечно малом ) изменении значения y функции, соответствующем бесконечно малому изменению dx. в аргументе функции x . По этой причине мгновенная скорость изменения y по отношению к x , которая является значением производной функции , обозначается дробью

$${\frac {dy}{dx}}$$

в так называемой нотации Лейбница для производных. Частное $dy/dx$не является бесконечно малым; скорее это реальное число .

Использование бесконечно малых в этой форме подверглось широкой критике, например, в знаменитой брошюре «Аналитик» епископа Беркли . Огюстен-Луи Коши ( 1823 ) определил дифференциал, не обращаясь к атомизму бесконечно малых Лейбница. Вместо этого Коши, вслед за Даламбером , перевернул логический порядок Лейбница и его последователей: производная сама стала фундаментальным объектом, определяемым как предел разностных коэффициентов, а затем через него определялись дифференциалы. То есть можно было свободно определять дифференциал $dy$ по выражению

$$dy=f'(x)\,dx$$

в котором $dy$ и $dx$ это просто новые переменные, принимающие конечные действительные значения, не фиксированные бесконечно малые величины, как это было у Лейбница.

По мнению Бойера (1959 , стр. 12), подход Коши был значительным логическим улучшением по сравнению с бесконечно малым подходом Лейбница, поскольку вместо обращения к метафизическому понятию бесконечно малых величин величины $dy$ и $dx$теперь можно манипулировать точно так же, как и любыми другими реальными величинами. осмысленным образом. Общий концептуальный подход Коши к дифференциалам остается стандартным в современных аналитических подходах. хотя последнее слово о строгости, вполне современном понятии предела, в конечном счете принадлежало Карлу Вейерштрассу .

В физических подходах, например, в теории термодинамики , по-прежнему преобладает точка зрения на бесконечно малые величины. Курант и Джон (1999 , стр. 184) примиряют физическое использование бесконечно малых дифференциалов с их математической невозможностью следующим образом. Дифференциалы представляют собой конечные ненулевые значения, которые меньше степени точности, необходимой для конкретной цели, для которой они предназначены. Таким образом, «физические бесконечно малые» не обязательно апеллируют к соответствующим математическим бесконечно малым, чтобы иметь точный смысл.

После достижений двадцатого века в области математического анализа и дифференциальной геометрии стало ясно, что понятие дифференциала функции можно расширить различными способами. В реальном анализе целесообразнее иметь дело непосредственно с дифференциалом как с главной частью приращения функции. Это непосредственно приводит к представлению о том, что дифференциал функции в точке является линейным функционалом от приращения $\Delta x$. Этот подход позволяет разрабатывать дифференциал (как линейное отображение) для множества более сложных пространств, что в конечном итоге приводит к появлению таких понятий, как производная Фреше или Гато . Точно так же в дифференциальной геометрии дифференциал функции в точке является линейной функцией касательного вектора («бесконечно малое смещение»), что демонстрирует его как своего рода одну форму: внешнюю производную функции. В нестандартном исчислении дифференциалы рассматриваются как бесконечно малые, которым самим можно поставить строгие основания (см. дифференциал (бесконечно малый) ).

Определение

Дифференциал функции $f(x)$ в какой-то момент $x_{0}$.

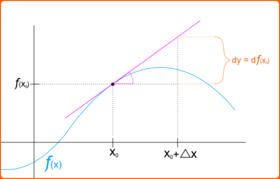
Дифференциал определяется в современных трактовках дифференциального исчисления следующим образом. Дифференциал функции $f(x)$ одной действительной переменной $x$ это функция $df$ двух независимых действительных переменных $x$ и $\Delta x$ данный

$$df(x,\Delta x)\ {\stackrel {\mathrm {def} }{=}}\ f'(x)\,\Delta x.$$

Один или оба аргумента могут быть подавлены, т. е. можно увидеть $df(x)$ или просто $df$. Если $y=f(x)$, дифференциал также можно записать как $dy$. С $dx(x,\Delta x)=\Delta x$, принято писать $dx=\Delta x$ так что имеет место следующее равенство:

$$df(x)=f'(x)\,dx$$

Это понятие дифференциала широко применимо, когда ищется линейное приближение к функции, в которой значение приращения $\Delta x$достаточно мал. Точнее, если $f$ является дифференцируемой функцией при $x$, то разница в $y$-ценности

$$\Delta y\ {\stackrel {\rm {def}}{=}}\ f(x+\Delta x)-f(x)$$

удовлетворяет

$$\Delta y=f'(x)\,\Delta x+\varepsilon =df(x)+\varepsilon \,$$

где ошибка $\varepsilon$ в приближении удовлетворяет $\varepsilon /\Delta x\rightarrow 0$ как $\Delta x\rightarrow 0$. Другими словами, имеется приблизительное тождество

$$\Delta y\approx dy$$

при котором погрешность можно сделать сколь угодно малой относительно $\Delta x$ ограничивая $\Delta x$быть достаточно маленьким; то есть,

$${\frac {\Delta y-dy}{\Delta x}}\to 0$$

как $\Delta x\rightarrow 0$. По этой причине дифференциал функции известен как главная (линейная) часть приращения функции: дифференциал является линейной функцией приращения функции. $\Delta x$, и хотя ошибка $\varepsilon$ может быть нелинейным, оно быстро стремится к нулю, поскольку $\Delta x$ стремится к нулю.

Дифференциалы в нескольких переменных

Оператор/Функция	$f(x)$	$f(x,y,u(x,y),v(x,y))$
Дифференциал	1: $df\,{\overset {\underset {\mathrm {def} }{}}{=}}\,f'_{x}\,dx$	2: $d_{x}f\,{\overset {\underset {\mathrm {def} }{}}{=}}\,f'_{x}\,dx$ 3: $df\,{\overset {\underset {\mathrm {def} }{}}{=}}\,f'_{x}dx+f'_{y}dy+f'_{u}du+f'_{v}dv$
Частная производная	$f'_{x}\,{\overset {\underset {\mathrm {(1)} }{}}{=}}\,{\frac {df}{dx}}$	$f'_{x}\,{\overset {\underset {\mathrm {(2)} }{}}{=}}\,{\frac {d_{x}f}{dx}}={\frac {\partial f}{\partial x}}$
Полная производная	${\frac {df}{dx}}\,{\overset {\underset {\mathrm {(1)} }{}}{=}}\,f'_{x}$	${\frac {df}{dx}}\,{\overset {\underset {\mathrm {(3)} }{}}{=}}\,f'_{x}+f'_{u}{\frac {du}{dx}}+f'_{v}{\frac {dv}{dx}};(f'_{y}{\frac {dy}{dx}}=0)$

Следуя Гурса (1904 , I, §15), для функций более чем одной независимой переменной:

$$y=f(x_{1},\dots ,x_{n}),$$

Частный дифференциал y y по любой из переменных x ₁ является основной частью изменения в результате изменения dx ₁ в этой переменной. Частный дифференциал, следовательно,

$${\frac {\partial y}{\partial x_{1}}}dx_{1}$$

включая производную y . по x ₁ частную Сумма частных дифференциалов по всем независимым переменным представляет собой полный дифференциал.

$$dy={\frac {\partial y}{\partial x_{1}}}dx_{1}+\cdots +{\frac {\partial y}{\partial x_{n}}}dx_{n},$$

что является основной частью изменения y в результате изменений независимых переменных x _i .

Точнее, в контексте исчисления многих переменных, следуя Куранту (1937b) , если f — дифференцируемая функция, то по определению дифференцируемости приращение

$${\begin{aligned}\Delta y&{}~{\stackrel {\mathrm {def} }{=}}~f(x_{1}+\Delta x_{1},\dots ,x_{n}+\Delta x_{n})-f(x_{1},\dots ,x_{n})\\&{}={\frac {\partial y}{\partial x_{1}}}\Delta x_{1}+\cdots +{\frac {\partial y}{\partial x_{n}}}\Delta x_{n}+\varepsilon _{1}\Delta x_{1}+\cdots +\varepsilon _{n}\Delta x_{n}\end{aligned}}$$

где члены ошибки ε   _i стремятся к нулю, поскольку приращения Δ x _i совместно стремятся к нулю. Тогда полный дифференциал строго определяется как

$$dy={\frac {\partial y}{\partial x_{1}}}\Delta x_{1}+\cdots +{\frac {\partial y}{\partial x_{n}}}\Delta x_{n}.$$

Поскольку согласно этому определению

$$dx_{i}(\Delta x_{1},\dots ,\Delta x_{n})=\Delta x_{i},$$

надо

$$dy={\frac {\partial y}{\partial x_{1}}}\,dx_{1}+\cdots +{\frac {\partial y}{\partial x_{n}}}\,dx_{n}.$$

Как и в случае с одной переменной, справедливо приблизительное тождество

$$dy\approx \Delta y$$

при котором общую ошибку можно сделать сколь угодно малой по отношению к ${\textstyle {\sqrt {\Delta x_{1}^{2}+\cdots +\Delta x_{n}^{2}}}}$ ограничивая внимание достаточно малыми приращениями.

Применение общего дифференциала

При измерении общий дифференциал используется для оценки погрешности. $\Delta f$ функции $f$ на основе ошибок $\Delta x,\Delta y,\ldots$ параметров $x,y,\ldots$. Предполагая, что интервал достаточно короткий, чтобы изменение было примерно линейным:

$$\Delta f(x)=f'(x)\Delta x$$

и что все переменные независимы, то для всех переменных

$$\Delta f=f_{x}\Delta x+f_{y}\Delta y+\cdots$$

Это потому, что производная $f_{x}$ по конкретному параметру $x$ дает чувствительность функции $f$ к изменению $x$, в частности ошибка $\Delta x$. Поскольку предполагается, что они независимы, анализ описывает наихудший сценарий. Используются абсолютные значения погрешностей составляющих, поскольку после простого вычисления производная может иметь отрицательный знак. Из этого принципа выводятся правила ошибок суммирования, умножения и т. д., например:

Позволять $f(a,b)=ab$. Тогда конечную ошибку можно аппроксимировать как

$$\Delta f=f_{a}\Delta a+f_{b}\Delta b.$$

Оценка производных:

$$\Delta f=b\Delta a+a\Delta b.$$

Деление на f , которое равно a × b

$${\frac {\Delta f}{f}}={\frac {\Delta a}{a}}+{\frac {\Delta b}{b}}$$

То есть при умножении общая относительная ошибка представляет собой сумму относительных ошибок параметров.

Чтобы проиллюстрировать, как это зависит от рассматриваемой функции, рассмотрим случай, когда функция равна $f(a,b)=a\ln b$вместо. Затем можно вычислить, что оценка ошибки равна

$${\frac {\Delta f}{f}}={\frac {\Delta a}{a}}+{\frac {\Delta b}{b\ln b}}$$

с дополнительным коэффициентом ' ln b ', которого нет в случае простого продукта. Этот дополнительный фактор имеет тенденцию уменьшать ошибку, поскольку ln b не так велик, как голый b .

Дифференциалы высшего порядка

Дифференциалы высшего порядка функции y = f ( x ) одной переменной x могут быть определены через:

$$d^{2}y=d(dy)=d(f'(x)dx)=(df'(x))dx=f''(x)\,(dx)^{2},$$

и вообще,

$$d^{n}y=f^{(n)}(x)\,(dx)^{n}.$$

Неформально это мотивирует обозначения Лейбница для производных более высокого порядка.

$$f^{(n)}(x)={\frac {d^{n}f}{dx^{n}}}.$$

Когда самой независимой переменной x разрешается зависеть от других переменных, выражение становится более сложным, поскольку оно должно включать также дифференциалы более высокого порядка в самой x . Так, например,

$${\begin{aligned}d^{2}y&=f''(x)\,(dx)^{2}+f'(x)d^{2}x\\[1ex]d^{3}y&=f'''(x)\,(dx)^{3}+3f''(x)dx\,d^{2}x+f'(x)d^{3}x\end{aligned}}$$

и так далее.

Аналогичные соображения применимы и к определению дифференциалов более высокого порядка функций нескольких переменных. Например, если f — функция двух переменных x и y , то

$$d^{n}f=\sum _{k=0}^{n}{\binom {n}{k}}{\frac {\partial ^{n}f}{\partial x^{k}\partial y^{n-k}}}(dx)^{k}(dy)^{n-k},$$

где ${\textstyle {\binom {n}{k}}}$является биномиальным коэффициентом . Для большего количества переменных справедливо аналогичное выражение, но с соответствующим полиномиальным, а не биномиальным разложением.

Дифференциалы более высокого порядка в нескольких переменных также усложняются, когда независимым переменным разрешается зависеть от других переменных. Например, для функции f от x и y , которой разрешено зависеть от вспомогательных переменных, имеем

$$d^{2}f=\left({\frac {\partial ^{2}f}{\partial x^{2}}}(dx)^{2}+2{\frac {\partial ^{2}f}{\partial x\partial y}}dx\,dy+{\frac {\partial ^{2}f}{\partial y^{2}}}(dy)^{2}\right)+{\frac {\partial f}{\partial x}}d^{2}x+{\frac {\partial f}{\partial y}}d^{2}y.$$

Из-за этой неуклюжести обозначений использование дифференциалов более высокого порядка подверглось резкой критике со стороны Адамара (1935) , который пришел к выводу:

Наконец, что означает или представляет собой равенство?

$$d^{2}z=r\,dx^{2}+2s\,dx\,dy+t\,dy^{2}\,?$$

По-моему, вообще ничего.

То есть: Наконец, что подразумевается или представлено равенством [...]? По-моему, вообще ничего. Несмотря на этот скептицизм, дифференциалы более высокого порядка все же стали важным инструментом анализа.

В этих контекстах дифференциал n -го порядка функции f , примененной к приращению Δ x, определяется выражением

$$d^{n}f(x,\Delta x)=\left.{\frac {d^{n}}{dt^{n}}}f(x+t\Delta x)\right|_{t=0}$$

или эквивалентное выражение, например

$$\lim _{t\to 0}{\frac {\Delta _{t\Delta x}^{n}f}{t^{n}}}$$

где $\Delta _{t\Delta x}^{n}f$ представляет собой n -ю прямую разность с приращением t Δ x .

Это определение имеет смысл и в том случае, если f — функция нескольких переменных (здесь для простоты рассматривается как векторный аргумент). Тогда n таким образом -й дифференциал является однородной функцией степени n по приращению вектора ∆x . определенный Кроме того, ряд Тейлора функции f в точке x определяется выражением

$$f(x+\Delta x)\sim f(x)+df(x,\Delta x)+{\frac {1}{2}}d^{2}f(x,\Delta x)+\cdots +{\frac {1}{n!}}d^{n}f(x,\Delta x)+\cdots$$

более высокого порядка Производная Гато обобщает эти соображения на бесконечномерные пространства.

Свойства

Ряд свойств дифференциала непосредственно вытекает из соответствующих свойств производной, частной производной и полной производной. К ним относятся:

• Линейность : для констант a и b и дифференцируемых функций f и g :
  $$d(af+bg)=a\,df+b\,dg.$$
• Правило произведения : для двух дифференцируемых f и g функций
  $$d(fg)=f\,dg+g\,df.$$

Операция d с этими двумя свойствами известна в абстрактной алгебре как дифференцирование . Они подразумевают правило власти

$$d(f^{n})=nf^{n-1}df$$

различные формы цепного правила : Кроме того, с возрастающей степенью общности применяются

• Если y = f ( u ) — дифференцируемая функция переменной u , а u = g ( x ) — дифференцируемая функция от x , то
  $$dy=f'(u)\,du=f'(g(x))g'(x)\,dx.$$
• Если y = f ( x1 _, , xn _... ) и все переменные x1 _{правилу} ..., xn _, зависят от другой переменной t , то по цепочки для частных производных имеем
  $${\begin{aligned}dy={\frac {dy}{dt}}dt&={\frac {\partial y}{\partial x_{1}}}dx_{1}+\cdots +{\frac {\partial y}{\partial x_{n}}}dx_{n}\\[1ex]&={\frac {\partial y}{\partial x_{1}}}{\frac {dx_{1}}{dt}}\,dt+\cdots +{\frac {\partial y}{\partial x_{n}}}{\frac {dx_{n}}{dt}}\,dt.\end{aligned}}$$
  Эвристически правило цепочки для нескольких переменных можно понять, разделив обе части этого уравнения на бесконечно малую величину dt .
• Имеют место более общие аналогичные выражения, в которых промежуточные переменные x _i зависят более чем от одной переменной.

Общая формулировка

См. Также: производная Фреше и производная Гато.

Непротиворечивое понятие дифференциала можно разработать для функции f : R ^н → Р ^м между двумя евклидовыми пространствами . Пусть x ,Δ x ∈ R ^н быть парой евклидовых векторов . Приращение функции f равно

$$\Delta f=f(\mathbf {x} +\Delta \mathbf {x} )-f(\mathbf {x} ).$$

Если существует размера m × n матрица A такая, что

$$\Delta f=A\Delta \mathbf {x} +\|\Delta \mathbf {x} \|{\boldsymbol {\varepsilon }}$$

котором вектор ε → 0 при Δx в → 0 , то f по определению дифференцируема в точке x . Матрицу A иногда называют матрицей Якобиана , а линейное преобразование , которое соответствует приращению Δ x ∈ R ^н вектор A ∆ x ∈ R ^м в этой общей ситуации известен как дифференциал df ( x ) функции f в точке x . Это и есть производная Фреше , и ту же самую конструкцию можно использовать для функции между любыми банаховыми пространствами .

Другая плодотворная точка зрения состоит в том, чтобы определить дифференциал непосредственно как своего рода производную по направлению :

$$df(\mathbf {x} ,\mathbf {h} )=\lim _{t\to 0}{\frac {f(\mathbf {x} +t\mathbf {h} )-f(\mathbf {x} )}{t}}=\left.{\frac {d}{dt}}f(\mathbf {x} +t\mathbf {h} )\right|_{t=0},$$

это подход, который уже использовался для определения дифференциалов более высокого порядка (и наиболее близок к определению, данному Коши). Если t представляет время и x положение , то h представляет собой скорость, а не смещение, как мы считали его до сих пор. Это дает еще одно уточнение понятия дифференциала: он должен быть линейной функцией кинематической скорости. Набор всех скоростей, проходящих через данную точку пространства, известен как касательное пространство , и поэтому df дает линейную функцию в касательном пространстве: дифференциальную форму . При такой интерпретации дифференциал f известен как внешняя производная и имеет широкое применение в дифференциальной геометрии , поскольку понятие скоростей и касательного пространства имеет смысл на любом дифференцируемом многообразии . Если, кроме того, выходное значение f также представляет положение (в евклидовом пространстве), то анализ размерностей подтверждает, что выходное значение df должно быть скоростью. Если рассматривать дифференциал таким образом, то он известен как pushforward , поскольку он «выталкивает» скорости из исходного пространства в скорости в целевом пространстве.

Другие подходы

Основная статья: Дифференциал (бесконечно малый)

Хотя понятие бесконечно малого приращения dx не имеет четкого определения в современном математическом анализе , существует множество методов определения бесконечно малого дифференциала , чтобы дифференциал функции можно было обрабатывать способом, не противоречащим обозначениям Лейбница. . К ним относятся:

• Определение дифференциала как разновидности дифференциальной формы , в частности внешней производной функции. Затем бесконечно малые приращения идентифицируются с векторами в касательном пространстве в точке. Этот подход популярен в дифференциальной геометрии и смежных областях, поскольку его легко обобщать на отображения между дифференцируемыми многообразиями .
• Дифференциалы как нильпотентные элементы коммутативных колец . Этот подход популярен в алгебраической геометрии .
• Дифференциалы в гладких моделях теории множеств. Этот подход известен как синтетическая дифференциальная геометрия или гладкий бесконечно малый анализ и тесно связан с алгебро-геометрическим подходом, за исключением того, что идеи теории топоса используются для сокрытия механизмов, с помощью которых вводятся нильпотентные бесконечно малые.
• Дифференциалы как бесконечно малые в гипердействительных системах счисления, которые являются расширениями действительных чисел и содержат обратимые бесконечно малые и бесконечно большие числа. Это подход нестандартного анализа, впервые предложенный Абрахамом Робинсоном .

Примеры и приложения

Дифференциалы могут эффективно использоваться в численном анализе для изучения распространения экспериментальных ошибок в расчетах и, следовательно, общей численной устойчивости задачи ( Courant 1937a ). Предположим, что переменная x представляет собой результат эксперимента, а y – результат численного вычисления, примененного к x . Вопрос в том, в какой степени ошибки измерения x влияют на результат вычисления y . Если x известен с точностью до Δ x от его истинного значения, то теорема Тейлора дает следующую оценку ошибки Δ y при вычислении y :

$$\Delta y=f'(x)\Delta x+{\frac {(\Delta x)^{2}}{2}}f''(\xi )$$

где ξ = x + θ Δ x для некоторого 0 < θ < 1 . Если Δ x мало, то членом второго порядка можно пренебречь, так что Δ y для практических целей хорошо аппроксимируется выражением dy = f' ( x ) Δ x .

Дифференциал часто бывает полезен при переписывании дифференциального уравнения.

$${\frac {dy}{dx}}=g(x)$$

в виде

$$dy=g(x)\,dx,$$

в частности, когда кто-то хочет разделить переменные .

См. также

• Обозначения для дифференцирования

Ссылки

• Бойер, Карл Б. (1959), История исчисления и его концептуальное развитие , Нью-Йорк: Dover Publications , MR   0124178 .
• Коши, Огюстен-Луи (1823), Краткое изложение уроков, проведенных в Королевской политехнической школе по применению исчисления бесконечно малых , заархивировано из оригинала 8 июля 2007 г. , получено 19 августа 2009 г.
• Курант, Ришар (1937a), Дифференциальное и интегральное исчисление. Том. Я , Библиотека классики Wiley, Нью-Йорк: John Wiley & Sons (опубликовано в 1988 г.), ISBN  978-0-471-60842-4 , МР   1009558 .
• Курант, Ришар (1937b), Дифференциальное и интегральное исчисление. Том. II , Библиотека классики Wiley, Нью-Йорк: John Wiley & Sons (опубликовано в 1988 г.), ISBN  978-0-471-60840-0 , МР   1009559 .
• Курант, Ричард ; Джон, Фриц (1999), Введение в исчисление и анализ, том 1 , Классика математики, Берлин, Нью-Йорк: Springer-Verlag , ISBN  3-540-65058-Х , МР   1746554
• Эйзенбуд, Дэвид ; Харрис, Джо (1998), Геометрия схем , Springer-Verlag, ISBN  0-387-98637-5 .
• Фреше, Морис (1925), «Понятие дифференциала в общем анализе», Annales Scientifiques de l'École Normale Supérieure , Series 3, 42 : 293–323, doi : 10.24033/asens.766 , ISSN   0012-9593 , MR   1509268 .
• Гурса, Эдуард (1904), Курс математического анализа: Том 1: Производные и дифференциалы, определенные интегралы, разложение в ряд, приложения к геометрии , Э. Р. Хедрик, Нью-Йорк: Dover Publications (опубликовано в 1959 г.), MR   0106155 .
• Адамар, Жак (1935), «Понятие дифференциала в обучении», Mathematical Gazette , XIX (236): 341–342, doi : 10.2307/3606323 , JSTOR   3606323 .
• Харди, Годфри Гарольд (1908), Курс чистой математики , издательство Кембриджского университета , ISBN  978-0-521-09227-2 .
• Хилле, Эйнар ; Филлипс, Ральф С. (1974), Функциональный анализ и полугруппы , Провиденс, Род-Айленд: Американское математическое общество , MR   0423094 .
• Ито, Киёси (1993), Энциклопедический математический словарь (2-е изд.), MIT Press , ISBN  978-0-262-59020-4 .
• Клайн, Моррис (1977), «Глава 13: Дифференциалы и закон среднего», Исчисление: интуитивный и физический подход , Джон Уайли и сыновья .
• Клайн, Моррис (1972), Математическая мысль от древних до наших дней (3-е изд.), Oxford University Press (опубликовано в 1990 г.), ISBN  978-0-19-506136-9
• Кейслер, Х. Джером (1986), Элементарное исчисление: бесконечно малый подход (2-е изд.) .
• Кок, Андерс (2006), Синтетическая дифференциальная геометрия (PDF) (2-е изд.), Cambridge University Press .
• Мурдейк, И .; Рейес, GE (1991), Модели для гладкого бесконечно малого анализа , Springer-Verlag .
• Робинсон, Абрахам (1996), Нестандартный анализ , Princeton University Press , ISBN  978-0-691-04490-3 .
• Толстов, Г.П. (2001) [1994], «Дифференциал» , Энциклопедия Математики , EMS Press .

Внешние ссылки

• Дифференциал функции в демонстрационном проекте Wolfram