Сопутствующие тарифы

В дифференциальном исчислении задачи , связанные со ставками , включают в себя определение скорости изменения величины путем соотнесения этой величины с другими величинами, скорость изменения которых известна. Скорость изменения обычно зависит от времени . Поскольку наука и техника часто связывают величины друг с другом, методы связанных скоростей имеют широкое применение в этих областях. Дифференциация по времени или одной из других переменных требует применения правила цепочки : ^[1] поскольку большинство задач связаны с несколькими переменными.

По сути, если функция $F$ определяется так, что $F=f(x)$ , то производная функции $F$ можно взять относительно другой переменной. Мы предполагаем $x$ является функцией $t$ , то есть $x=g(t)$ . Затем $F=f(g(t))$ , так

F'(t)=f'(g(t))\cdot g'(t)

Записанное в обозначениях Лейбница, это:

{\frac {dF}{dt}}={\frac {df}{dx}}\cdot {\frac {dx}{dt}}.

Таким образом, если известно, как $x$ изменения по отношению к $t$ , то мы сможем определить, как $F$ изменения по отношению к $t$ и наоборот. Мы можем расширить это применение цепного правила с помощью правил исчисления суммы, разности, произведения и частного и т. д.

Например, если $F(x)=G(y)+H(z)$ затем

{\frac {dF}{dx}}\cdot {\frac {dx}{dt}}={\frac {dG}{dy}}\cdot {\frac {dy}{dt}}+{\frac {dH}{dz}}\cdot {\frac {dz}{dt}}.

Процедура [ править ]

Наиболее распространенный способ решения проблем, связанных со ставками, заключается в следующем: ^[2]

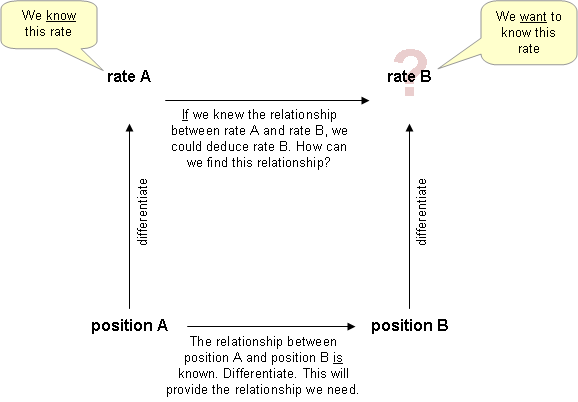
Определите известные переменные , включая скорость изменения и скорость изменения, которую необходимо найти. (Рисование изображения или изображения проблемы может помочь сохранить все в порядке)
Постройте уравнение, связывающее величины, скорость изменения которых известна, с величиной, скорость изменения которой необходимо найти.
Дифференцируйте обе части уравнения по времени (или другой скорости изменения). Часто цепное правило . на этом этапе применяется
Подставьте в уравнение известные скорости изменения и известные величины.
Определите желаемую скорость изменения.

Ошибки в этой процедуре часто возникают из-за подстановки известных значений переменных до (а не после) нахождения производной по времени. Это приведет к неправильному результату, поскольку, если эти значения заменить переменные перед дифференцированием, эти переменные станут константами; а когда уравнение дифференцируется, на местах всех переменных, для которых были подставлены значения, появляются нули.

Пример [ править ]

10-метровая лестница прислонена к стене здания, а основание лестницы отъезжает от здания со скоростью 3 метра в секунду. С какой скоростью верхняя часть лестницы скатится вниз по стене, если ее основание находится на расстоянии 6 метров от стены?

Расстояние между основанием лестницы и стеной x и высота лестницы на стене y представляют собой стороны прямоугольного треугольника , в котором лестница является гипотенузой h . Цель состоит в том, чтобы найти dy / dt , скорость изменения y относительно времени t , когда h , x и dx / dt , скорость изменения x известны .

Шаг 1:

$x=6$
$h=10$
${\frac {dx}{dt}}=3$
${\frac {dh}{dt}}=0$
${\frac {dy}{dt}}={\text{?}}$

Шаг 2:Из теоремы Пифагора уравнение

x^{2}+y^{2}=h^{2},

описывает взаимосвязь между x , y и h для прямоугольного треугольника. Дифференцируя обе части этого уравнения по времени t , получаем

{\frac {d}{dt}}\left(x^{2}+y^{2}\right)={\frac {d}{dt}}\left(h^{2}\right)

Шаг 3:При решении желаемой скорости изменения dy / dt дает нам

{\frac {d}{dt}}\left(x^{2}\right)+{\frac {d}{dt}}\left(y^{2}\right)={\frac {d}{dt}}\left(h^{2}\right)

(2x){\frac {dx}{dt}}+(2y){\frac {dy}{dt}}=(2h){\frac {dh}{dt}}

x{\frac {dx}{dt}}+y{\frac {dy}{dt}}=h{\frac {dh}{dt}}

{\frac {dy}{dt}}={\frac {h{\frac {dh}{dt}}-x{\frac {dx}{dt}}}{y}}.

Шаг 4 и 5:Использование переменных из шага 1 дает нам:

{\frac {dy}{dt}}={\frac {h{\frac {dh}{dt}}-x{\frac {dx}{dt}}}{y}}.

{\frac {dy}{dt}}={\frac {10\times 0-6\times 3}{y}}=-{\frac {18}{y}}.

Решение для y с использованием теоремы Пифагора дает:

x^{2}+y^{2}=h^{2}

6^{2}+y^{2}=10^{2}

y=8

Подставим 8 в уравнение:

-{\frac {18}{y}}=-{\frac {18}{8}}=-{\frac {9}{4}}

Обычно предполагается, что отрицательные значения представляют собой нисходящее направление. При этом верхняя часть лестницы скользит вниз по стене со скоростью 9/4 метра в секунду .

Примеры по физике [ править ]

Поскольку одна физическая величина часто зависит от другой, которая, в свою очередь, зависит от других, таких как время, методы связанных скоростей имеют широкое применение в физике. В этом разделе представлен пример связанных скоростей кинематики и электромагнитной индукции .

Относительная кинематика двух транспортных средств [ править ]

Например, можно рассмотреть задачу кинематики, где одно транспортное средство движется на запад к перекрестку со скоростью 80 миль в час, а другое движется на север от перекрестка со скоростью 60 миль в час. Можно спросить, приближаются ли транспортные средства друг к другу или дальше и с какой скоростью в тот момент, когда транспортное средство, направляющееся на север, находится в 3 милях к северу от перекрестка, а транспортное средство, направляющееся на запад, находится в 4 милях к востоку от перекрестка.

Большая идея: использовать цепное правило для вычисления скорости изменения расстояния между двумя транспортными средствами.

План:

Выберите систему координат
Определить переменные
Нарисовать картинку
Большая идея: использовать цепное правило для вычисления скорости изменения расстояния между двумя транспортными средствами.
Выразите c через x и y с помощью теоремы Пифагора.
Выразите dc / dt, используя цепное правило, через dx / dt и dy / dt.
Подставить в x , y , dx / dt , dy / dt
Упрощать.

Выберите систему координат: Пусть ось Y указывает на север, а ось X указывает на восток.

Определите переменные: Определите y ( t ) как расстояние транспортного средства, направляющегося на север от начала координат, и x ( t ) как расстояние транспортного средства, направляющегося на запад от начала координат.

Выразите c через x и y с помощью теоремы Пифагора:

c=\left(x^{2}+y^{2}\right)^{1/2}

Выразите dc / dt, используя цепное правило, через dx / dt и dy/dt:

${\frac {dc}{dt}}={\frac {d}{dt}}\left(x^{2}+y^{2}\right)^{1/2}$	Применить оператор производной ко всей функции
$={\frac {1}{2}}\left(x^{2}+y^{2}\right)^{-1/2}{\frac {d}{dt}}\left(x^{2}+y^{2}\right)$	Квадратный корень является внешней функцией; Сумма квадратов находится внутри функции
$={\frac {1}{2}}\left(x^{2}+y^{2}\right)^{-1/2}\left[{\frac {d}{dt}}(x^{2})+{\frac {d}{dt}}(y^{2})\right]$	Распределить оператор дифференцирования
$={\frac {1}{2}}\left(x^{2}+y^{2}\right)^{-1/2}\left[2x{\frac {dx}{dt}}+2y{\frac {dy}{dt}}\right]$	Примените цепное правило к x ( t ) и y ( t )}
$={\frac {x{\frac {dx}{dt}}+y{\frac {dy}{dt}}}{\sqrt {x^{2}+y^{2}}}}$	Упрощать.

Замените x = 4 мили, y = 3 мили, dx / dt = −80 миль/ч, dy / dt = 60 миль/ч и упростите.

{\begin{aligned}{\frac {dc}{dt}}&={\frac {4{\text{ mi}}\cdot (-80{\text{ mi}}/{\text{hr}})+3{\text{ mi}}\cdot (60){\text{mi}}/{\text{hr}}}{\sqrt {(4{\text{ mi}})^{2}+(3{\text{ mi}})^{2}}}}\\&={\frac {-320{\text{ mi}}^{2}/{\text{hr}}+180{\text{ mi}}^{2}/{\text{hr}}}{5{\text{ mi}}}}\\&={\frac {-140{\text{ mi}}^{2}/{\text{hr}}}{5{\text{ mi}}}}\\&=-28{\text{ mi}}/{\text{hr}}\end{aligned}}

Следовательно, два автомобиля приближаются друг к другу со скоростью 28 миль в час.

индукция вращения проводящей петли в магнитном поле Электромагнитная

Магнитный поток через петлю площадью A , нормаль которой находится под углом θ к магнитному полю напряженностью B, равен

\Phi _{B}=BA\cos(\theta ),

Фарадея Закон электромагнитной индукции гласит, что наведенная электродвижущая сила ${\mathcal {E}}$ - отрицательная скорость изменения магнитного потока $\Phi _{B}$ через проводящую петлю.

{\mathcal {E}}=-{\frac {d\Phi _{B}}{dt}},

Если площадь петли A и магнитное поле B остаются постоянными, но петля вращается так, что угол θ является известной функцией времени, скорость изменения θ может быть связана со скоростью изменения $\Phi _{B}$ (и, следовательно, электродвижущую силу), взяв производную по времени соотношения потоков

{\mathcal {E}}=-{\frac {d\Phi _{B}}{dt}}=BA\sin \theta {\frac {d\theta }{dt}}

Если, например, петля вращается с постоянной угловой скоростью ω , так что θ = ωt , то

{\mathcal {E}}=\omega BA\sin \omega t

Ссылки [ править ]

^ «Сопутствующие тарифы» . Колледж Уитмена . Проверено 27 октября 2013 г.
^ Крайдер, Дональд. «Сопутствующие тарифы» . Дартмут . Проверено 27 октября 2013 г.

[1] «Сопутствующие тарифы» . Колледж Уитмена . Проверено 27 октября 2013 г.

[2] Крайдер, Дональд. «Сопутствующие тарифы» . Дартмут . Проверено 27 октября 2013 г.

[1]

[2]

v т и Исчисление
Precalculus	Binomial theorem Concave function Continuous function Factorial Finite difference Free variables and bound variables Graph of a function Linear function Radian Rolle's theorem Secant Slope Tangent
Limits	Indeterminate form Limit of a function One-sided limit Limit of a sequence Order of approximation (ε, δ)-definition of limit
Differential calculus	Derivative Second derivative Partial derivative Differential Differential operator Mean value theorem Notation Leibniz's notation Newton's notation Rules of differentiation linearity Power Sum Chain L'Hôpital's Product General Leibniz's rule Quotient Other techniques Implicit differentiation Inverse functions and differentiation Logarithmic derivative Related rates Stationary points First derivative test Second derivative test Extreme value theorem Maximum and minimum Further applications Newton's method Taylor's theorem Differential equation Ordinary differential equation Partial differential equation Stochastic differential equation
Integral calculus	Antiderivative Arc length Riemann integral Basic properties Constant of integration Fundamental theorem of calculus Differentiating under the integral sign Integration by parts Integration by substitution trigonometric Euler Tangent half-angle substitution Partial fractions in integration Quadratic integral Trapezoidal rule Volumes Washer method Shell method Integral equation Integro-differential equation
Vector calculus	Derivatives Curl Directional derivative Divergence Gradient Laplacian Basic theorems Line integrals Green's Stokes' Gauss'
Multivariable calculus	Divergence theorem Geometric Hessian matrix Jacobian matrix and determinant Lagrange multiplier Line integral Matrix Multiple integral Partial derivative Surface integral Volume integral Advanced topics Differential forms Exterior derivative Generalized Stokes' theorem Tensor calculus
Sequences and series	Arithmetico-geometric sequence Types of series Alternating Binomial Fourier Geometric Harmonic Infinite Power Maclaurin Taylor Telescoping Tests of convergence Abel's Alternating series Cauchy condensation Direct comparison Dirichlet's Integral Limit comparison Ratio Root Term
Special functions and numbers	Bernoulli numbers e (mathematical constant) Exponential function Natural logarithm Stirling's approximation
History of calculus	Adequality Brook Taylor Colin Maclaurin Generality of algebra Gottfried Wilhelm Leibniz Infinitesimal Infinitesimal calculus Isaac Newton Fluxion Law of Continuity Leonhard Euler Method of Fluxions The Method of Mechanical Theorems
Lists	Differentiation rules List of integrals of exponential functions List of integrals of hyperbolic functions List of integrals of inverse hyperbolic functions List of integrals of inverse trigonometric functions List of integrals of irrational functions List of integrals of logarithmic functions List of integrals of rational functions List of integrals of trigonometric functions Secant Secant cubed List of limits Lists of integrals
Miscellaneous topics	Complex calculus Contour integral Differential geometry Manifold Curvature of curves of surfaces Tensor Euler–Maclaurin formula Gabriel's horn Integration Bee Proof that 22/7 exceeds π Regiomontanus' angle maximization problem Steinmetz solid