Факториал

Чтобы узнать о других значениях, см. Факториал (значения) .

Выбранные факториалы; значения в научной записи округляются

$n$	$n!$
0	1
1	1
2	2
3	6
4	24
5	120
6	720
7	5 040
8	40 320
9	362 880
10	3 628 800
11	39 916 800
12	479 001 600
13	6 227 020 800
14	87 178 291 200
15	1 307 674 368 000
16	20 922 789 888 000
17	355 687 428 096 000
18	6 402 373 705 728 000
19	121 645 100 408 832 000
20	2 432 902 008 176 640 000
25	1.551 121 004 × 10 25
50	3.041 409 320 × 10 64
70	1.197 857 167 × 10 100
100	9.332 621 544 × 10 157
450	1.733 368 733 × 10 1 000
1 000	4.023 872 601 × 10 2 567
3 249	6.412 337 688 × 10 10 000
10 000	2.846 259 681 × 10 35 659
25 206	1.205 703 438 × 10 100 000
100 000	2.824 229 408 × 10 456 573
205 023	2.503 898 932 × 10 1 000 004
1 000 000	8.263 931 688 × 10 5 565 708
10 100	10 10 101.998 109 775 4820

В математике факториал целого неотрицательного числа $n$, обозначенный ​ $n!$, является произведением всех положительных целых чисел, меньших или равных $n$. Факториал ​ $n$ также равно произведению $n$ со следующим меньшим факториалом:

$${\begin{aligned}n!&=n\times (n-1)\times (n-2)\times (n-3)\times \cdots \times 3\times 2\times 1\\&=n\times (n-1)!\\\end{aligned}}$$

Например,

$$5!=5\times 4!=5\times 4\times 3\times 2\times 1=120.$$

Значение 0! равен 1 в соответствии с соглашением о пустом продукте .

Факториалы были обнаружены в нескольких древних культурах, особенно в индийской математике в канонических произведениях джайнской литературы и еврейскими мистиками в талмудической книге «Сефер Йецира» . Операция факториал встречается во многих областях математики, особенно в комбинаторике , где ее основное применение заключается в подсчете возможных различных последовательностей – перестановок – $n$ отдельные объекты: есть $n!$. В математическом анализе факториалы используются в степенных рядах для показательной функции и других функций, а также имеют приложения в алгебре , теории чисел , теории вероятностей и информатике .

Большая часть математики факториальной функции была разработана в конце 18 - начале 19 веков. Приближение Стирлинга обеспечивает точное приближение факториала больших чисел, показывая, что он растет быстрее, чем экспоненциальный рост . Формула Лежандра описывает показатели степени простых чисел при разложении факториалов на простые числа и может использоваться для подсчета конечных нулей факториалов. Даниэль Бернулли и Леонард Эйлер интерполировали факториальную функцию до непрерывной функции комплексных чисел , за исключением отрицательных целых чисел, (смещенной) гамма-функции .

Многие другие известные функции и числовые последовательности тесно связаны с факториалами, включая биномиальные коэффициенты , двойные факториалы , падающие факториалы , первоначальные числа и субфакториалы . Реализации функции факториала обычно используются в качестве примера различных стилей компьютерного программирования и включаются в научные калькуляторы и библиотеки программного обеспечения для научных вычислений. Хотя прямое вычисление больших факториалов с использованием формулы произведения или рекуррентного метода неэффективно, известны более быстрые алгоритмы, сопоставляющие с точностью до постоянного множителя время для быстрых алгоритмов умножения чисел с одинаковым количеством цифр.

История

Концепция факториалов возникла независимо во многих культурах:

• В индийской математике одно из самых ранних известных описаний факториалов взято из Ануйогадвара-сутры, одно из канонических произведений джайнской литературы , даты которого варьируются от 300 г. до н.э. до 400 г. н.э. Он отделяет отсортированный и обратный порядок набора предметов от других («смешанных») заказов, оценивая количество смешанных заказов путем вычитания двух из обычной формулы произведения для факториала. Правило произведения для перестановок было также описано джайнским монахом VI века н.э. Джинабхадрой . Индуистские ученые использовали формулы факториала, по крайней мере, с 1150 года, когда Бхаскара II упомянул факториалы в своей работе «Лилавати» в связи с проблемой того, сколькими способами Вишну мог удерживать свои четыре характерных объекта ( раковину , дискус , булаву и цветок лотоса) . ) в четырех руках, и аналогичная задача для десятирукого бога.
• В математике Ближнего Востока в еврейской мистической книге творения «Сефер Йецира» периода Талмуда (200–500 гг. н.э.) перечислены факториалы до 7! в рамках исследования количества слов, которые можно составить из еврейского алфавита . Факториалы также изучались по тем же причинам арабским грамматистом 8-го века Аль-Халилом ибн Ахмадом аль-Фарахиди . Арабский математик Ибн аль-Хайсам (также известный как Альхазен, ок. 965 – ок. 1040) был первым, кто сформулировал теорему Вильсона, связывающую факториалы с простыми числами .
• В Европе, хотя греческая математика включала в себя некоторую комбинаторику, а Платон , как известно, использовал 5040 (факториал) в качестве популяции идеального сообщества, отчасти из-за его свойств делимости, прямых свидетельств древнегреческого изучения факториалов нет. Вместо этого первая работа по факториалам в Европе была сделана еврейскими учёными, такими как Шаббатай Донноло , объясняющими отрывок из Сефер Йецира. В 1677 году британский писатель Фабиан Стедман описал применение факториалов для изменения звона — музыкальное искусство, включающее звон в несколько настроенных колоколов.

С конца 15 века факториалы стали предметом изучения западных математиков. В трактате 1494 года итальянский математик Лука Пачоли вычислил факториалы до 11! в связи с проблемой расположения обеденного стола. Кристофер Клавиус обсуждал факториалы в комментарии 1603 года к работе Иоганна де Сакробоско , а в 1640-х годах французский эрудит Марин Мерсенн опубликовал большие (но не совсем правильные) таблицы факториалов, до 64!, на основе работы Клавиуса. Степенной ряд для показательной функции с обратными факториалами для ее коэффициентов был впервые сформулирован в 1676 году Исааком Ньютоном в письме Готфриду Вильгельму Лейбницу . Другие важные работы ранней европейской математики по факториалам включают обширное освещение в трактате 1685 года Джона Уоллиса , исследование их приблизительных значений для больших значений $n$ Абрахама де Муавра в 1721 году, письмо Джеймса Стирлинга к де Муару в 1729 году, в котором излагается то, что стало известно как приближение Стирлинга , и одновременная работа Даниэля Бернулли и Леонарда Эйлера , формулирующая непрерывное расширение факториальной функции до гамма-функции . Адриен-Мари Лежандр включил формулу Лежандра , описывающую показатели степени факторизации факториалов в простые степени , в текст по теории чисел 1808 года .

Обозначения $n!$ Факториал был введен французским математиком Кристианом Крампом в 1808 году. Также использовались многие другие обозначения. Еще одна более поздняя запись $\vert \!{\underline {\,n}}$, в котором аргумент факториала был наполовину закрыт левой и нижней сторонами рамки, был популярен в течение некоторого времени в Великобритании и Америке, но вышел из употребления, возможно, из-за того, что его трудно печатать. Слово «факториал» (первоначально французское: Factorielle ) впервые было использовано в 1800 году Луи Франсуа Антуаном Арбогастом . в первой работе по формуле Фаа ди Бруно , но имея в виду более общее понятие произведений арифметических прогрессий . «Факторы», к которым относится это название, представляют собой условия формулы произведения факториала.

Определение

Факториал положительного целого числа $n$ определяется произведением всех натуральных чисел, не превышающих $n$

$$n!=1\cdot 2\cdot 3\cdots (n-2)\cdot (n-1)\cdot n.$$

Это можно записать более кратко в обозначениях продуктов как

$$n!=\prod _{i=1}^{n}i.$$

Если эту формулу произведения изменить, чтобы сохранить все члены, кроме последнего, она будет определять произведение той же формы, но с меньшим факториалом. Это приводит к рекуррентному соотношению , согласно которому каждое значение факториала можно получить умножением предыдущего значения на $n$:

$$n!=n\cdot (n-1)!.$$

Например, $5!=5\cdot 4!=5\cdot 24=120$.

Факториал нуля

Факториал ​ $0$ является $1$, или в символах, $0!=1$. Это определение имеет несколько мотивов:

• Для $n=0$, определение $n!$ поскольку продукт не включает в себя произведение вообще без чисел, и это является примером более широкого соглашения, согласно которому пустой продукт , продукт без множителей, равен мультипликативному тождеству.
• Существует ровно одна перестановка нулевых объектов: если нечего переставлять, единственная перестановка — это ничего не делать.
• Это соглашение делает многие тождества в комбинаторике действительными для любого допустимого выбора их параметров. Например, количество способов выбрать все $n$ элементы из набора $n$ является ${\textstyle {\tbinom {n}{n}}={\tfrac {n!}{n!0!}}=1,}$ тождество биномиального коэффициента , которое будет действительным только при $0!=1$.
• С $0!=1$, рекуррентное соотношение для факториала остается действительным при $n=1$. Следовательно, согласно этому соглашению, рекурсивное вычисление факториала должно иметь только нулевое значение в качестве базового случая , что упрощает вычисление и позволяет избежать необходимости в дополнительных особых случаях.
• Параметр $0!=1$ позволяет компактно выразить многие формулы, такие как показательная функция , в виде степенного ряда : ${\textstyle e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}.}$
• Этот выбор соответствует гамма-функции $0!=\Gamma (0+1)=1$, и гамма-функция должна иметь это значение, чтобы быть непрерывной функцией .

Приложения

Самое раннее использование функции факториала связано с подсчетом перестановок : существуют $n!$ разные способы организации $n$ отдельные объекты в последовательность. Факториалы появляются в более широком смысле во многих формулах комбинаторики , чтобы учитывать различный порядок объектов. Например, биномиальные коэффициенты ${\tbinom {n}{k}}$ посчитай $k$-элементные комбинации (подмножества $k$ элементы) из набора с $n$ элементы и могут быть вычислены из факториалов по формуле

$${\binom {n}{k}}={\frac {n!}{k!(n-k)!}}.$$

Числа Стирлинга первого рода суммируются с факториалами и подсчитывают перестановки $n$ сгруппированы в подмножества с одинаковым числом циклов. Другое комбинаторное применение — подсчет нарушений , перестановок, которые не оставляют ни один элемент в исходном положении; количество нарушений $n$ items — это ближайшее целое число к $n!/e$.

В алгебре факториалы возникают посредством биномиальной теоремы , которая использует биномиальные коэффициенты для расширения степеней сумм. Они также встречаются в коэффициентах, используемых для связи определенных семейств полиномов друг с другом, например, в тождествах Ньютона для симметричных многочленов . Их использование при подсчете перестановок также можно переформулировать алгебраически: факториалы — это порядки конечных симметрических групп . В исчислении факториалы встречаются в формуле Фаа ди Бруно для объединения высших производных. В математическом анализе факториалы часто появляются в знаменателях степенных рядов , особенно в рядах для показательной функции .

$$e^{x}=1+{\frac {x}{1}}+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+\cdots =\sum _{i=0}^{\infty }{\frac {x^{i}}{i!}},$$

и в коэффициентах других рядов Тейлора (в частности, тригонометрических и гиперболических функций ), где они сокращают множители $n!$ исходя из $n$-я производная от $x^{n}$. Такое использование факториалов в степенных рядах связано с аналитической комбинаторикой через экспоненциальную производящую функцию , которая для комбинаторного класса с $n_{i}$ элементы размера $i$ определяется как степенной ряд

$$\sum _{i=0}^{\infty }{\frac {x^{i}n_{i}}{i!}}.$$

В теории чисел наиболее важным свойством факториалов является делимость . $n!$ всеми положительными целыми числами до $n$, более точно описываемая для простых множителей формулой Лежандра . Отсюда следует, что сколь угодно большие простые числа можно найти как простые делители чисел. $n!\pm 1$, что привело к доказательству теоремы Евклида о том, что число простых чисел бесконечно. Когда $n!\pm 1$ само по себе простое число, оно называется факториалом простого числа ; соответственно, проблема Брокара , также поставленная Шринивасой Рамануджаном , касается существования квадратных чисел вида $n!+1$. Напротив, цифры $n!+2,n!+3,\dots n!+n$ все должны быть составными, что доказывает существование сколь угодно больших простых пробелов . Элементарное доказательство постулата Бертрана о существовании простого числа в любом интервале вида $[n,2n]$, один из первых результатов Пола Эрдеша , был основан на свойствах делимости факториалов. Факториальная система счисления представляет собой смешанную систему счисления для чисел, в которой разрядные значения каждой цифры являются факториалами.

Факториалы широко используются в теории вероятностей , например, в распределении Пуассона. и в вероятностях случайных перестановок . В информатике , помимо анализа переборов перестановок, факториалы возникают в нижней границе $\log _{2}n!=n\log _{2}n-O(n)$ от количества сравнений, необходимых для сравнительной сортировки набора $n$ предметы, и при анализе связанных хеш-таблиц , где распределение ключей на ячейку может быть точно аппроксимировано распределением Пуассона. Более того, факториалы естественным образом появляются в формулах квантовой и статистической физики , где часто рассматриваются все возможные перестановки набора частиц. В статистической механике расчеты энтропии , такие как формула энтропии Больцмана или уравнение Сакура-Тетроде, должны корректировать количество микросостояний путем деления на факториалы чисел каждого типа неразличимых частиц, чтобы избежать парадокса Гиббса . Квантовая физика объясняет, почему эти поправки необходимы.

Свойства

и

Сравнение факториала, приближения Стирлинга и более простого приближения $(n/e)^{n}$, в дважды логарифмическом масштабе

Относительная ошибка в усеченном ряду Стирлинга в зависимости от количества членов

Основная статья: Приближение Стирлинга

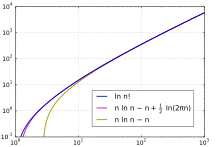
функции В качестве $n$Факториал растет быстрее, чем экспоненциальная функция , но растет медленнее, чем двойная экспоненциальная функция . Скорость его роста аналогична $n^{n}$, но медленнее в геометрической прогрессии. Один из способов приблизиться к этому результату — взять натуральный логарифм факториала, который превращает формулу его произведения в сумму, а затем оценить сумму с помощью интеграла:

$$\ln n!=\sum _{x=1}^{n}\ln x\approx \int _{1}^{n}\ln x\,dx=n\ln n-n+1.$$

Возведение результата в степень (и игнорирование незначительного $+1$ срок) приблизительно $n!$ как $(n/e)^{n}$. Более тщательное ограничение суммы сверху и снизу интегралом с использованием правила трапеций показывает, что для этой оценки необходим поправочный коэффициент, пропорциональный ${\sqrt {n}}$. Константу пропорциональности для этой поправки можно найти из произведения Уоллиса , которое выражает $\pi$как предельное соотношение факториалов и степеней двойки. Результатом этих поправок является приближение Стирлинга :

$$n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\,.$$

Здесь $\sim$ символ означает, что, поскольку $n$стремится к бесконечности, отношение между левой и правой частями в пределе приближается к единице . Формула Стирлинга дает первый член асимптотического ряда , который становится еще более точным, если принять его к большему числу членов:

$$n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\left(1+{\frac {1}{12n}}+{\frac {1}{288n^{2}}}-{\frac {139}{51840n^{3}}}-{\frac {571}{2488320n^{4}}}+\cdots \right).$$

Альтернативная версия использует в поправочных терминах только нечетные показатели:

$$n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\exp \left({\frac {1}{12n}}-{\frac {1}{360n^{3}}}+{\frac {1}{1260n^{5}}}-{\frac {1}{1680n^{7}}}+\cdots \right).$$

Многие другие варианты этих формул были также разработаны Шринивасой Рамануджаном , Биллом Госпером и другими.

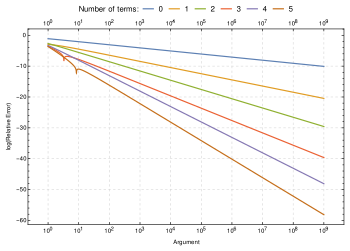
Двоичный логарифм факториала, используемый для анализа сортировки сравнения , можно очень точно оценить с помощью приближения Стирлинга. В приведенной ниже формуле $O(1)$ термин вызывает большое обозначение O.

$$\log _{2}n!=n\log _{2}n-(\log _{2}e)n+{\frac {1}{2}}\log _{2}n+O(1).$$

Делимость и цифры

Основная статья: формула Лежандра

Формула произведения факториала подразумевает, что $n!$ делится на все простые числа , не более $n$, и не большими простыми числами. Более точную информацию о его делимости дает формула Лежандра , которая дает показатель степени каждого простого числа. $p$ в простой факторизации $n!$ как

$$\sum _{i=1}^{\infty }\left\lfloor {\frac {n}{p^{i}}}\right\rfloor ={\frac {n-s_{p}(n)}{p-1}}.$$

Здесь $s_{p}(n)$ обозначает сумму основания - $p$ цифры ​ $n$, а показатель степени, заданный этой формулой, также можно интерпретировать в высшей математике как p -адическую оценку факториала. Применение формулы Лежандра к формуле произведения для биномиальных коэффициентов дает теорему Куммера , аналогичный результат о показателе степени каждого простого числа при факторизации биномиального коэффициента. Группирование простых множителей факториала в простые степени различными способами дает мультипликативное разбиение факториала .

Частный случай формулы Лежандра для $p=5$ дает количество конечных нулей в десятичном представлении факториалов. Согласно этой формуле количество нулей можно получить, вычитая цифры по основанию 5. $n$ от $n$, и разделив результат на четыре. Формула Лежандра подразумевает, что показатель степени простого числа $p=2$ всегда больше показателя степени $p=5$, поэтому каждый множитель пять можно соединить с множителем два, чтобы получить один из этих конечных нулей. Старшие цифры факториалов распределяются по закону Бенфорда . Любая последовательность цифр в любой базе есть последовательность начальных цифр некоторого факториала в этой базе.

Другой результат о делимости факториалов, теорема Вильсона , утверждает, что $(n-1)!+1$ делится на $n$ если и только если $n$ является простым числом . Для любого заданного целого числа $x$, Кемпнера функция ​ $x$ дается наименьшее $n$ для которого $x$ делит $n!$. Почти для всех чисел (кроме подмножества исключений с нулевой асимптотической плотностью ) оно совпадает с наибольшим простым множителем числа . $x$.

Произведение двух факториалов, $m!\cdot n!$, всегда делит поровну $(m+n)!$. Существует бесконечно много факториалов, равных произведению других факториалов: если $n$ сам по себе является произведением факториалов, то $n!$ равно тому же произведению, умноженному на еще один факториал, $(n-1)!$. Единственные известные примеры факториалов, которые являются произведениями других факториалов, но не имеют этой «тривиальной» формы: $9!=7!\cdot 3!\cdot 3!\cdot 2!$, $10!=7!\cdot 6!=7!\cdot 5!\cdot 3!$, и $16!=14!\cdot 5!\cdot 2!$. следовало бы abc Из гипотезы , что существует лишь конечное число нетривиальных примеров.

Наибольший общий делитель значений примитивного многочлена степени $d$ по целым числам делит нацело $d!$.

и нецелочисленное

Гамма-функция (сдвинутая на одну единицу влево для соответствия факториалам) непрерывно интерполирует факториал до нецелых значений.

Абсолютные значения комплексной гамма-функции с указанием полюсов в неположительных целых числах.

Основная статья: Гамма-функция

Существует бесконечно много способов расширить факториалы до непрерывной функции . Наиболее широко используемый из них использует гамма-функцию , которую для положительных действительных чисел можно определить как интеграл

$$\Gamma (z)=\int _{0}^{\infty }x^{z-1}e^{-x}\,dx.$$

Полученная функция связана с факториалом неотрицательного целого числа. $n$ по уравнению

$$n!=\Gamma (n+1),$$

который можно использовать как определение факториала для нецелых аргументов. При всех значениях $x$ для чего оба $\Gamma (x)$ и $\Gamma (x-1)$ определены, гамма-функция подчиняется функциональному уравнению

$$\Gamma (n)=(n-1)\Gamma (n-1),$$

обобщающее рекуррентное соотношение для факториалов.

Тот же интеграл сходится в более общем смысле для любого комплексного числа. $z$действительная часть которого положительна. Его можно распространить на нецелые точки в остальной части комплексной плоскости , решив формулу отражения Эйлера.

$$\Gamma (z)\Gamma (1-z)={\frac {\pi }{\sin \pi z}}.$$

Однако эту формулу нельзя использовать для целых чисел, поскольку для них $\sin \pi z$член приведет к делению на ноль . Результатом этого процесса расширения является аналитическая функция , аналитическое продолжение интегральной формулы для гамма-функции. Оно имеет ненулевое значение для всех комплексных чисел, за исключением неположительных целых чисел, где оно имеет простые полюса . Соответственно, это дает определение факториала для всех комплексных чисел, кроме отрицательных целых чисел. Одно свойство гамма-функции, отличающее ее от других непрерывных интерполяций факториалов, задается теоремой Бора – Моллерупа , которая утверждает, что гамма-функция (смещенная на единицу) является единственной логарифмически-выпуклой функцией для положительных действительных чисел, которая интерполирует факториалы и подчиняется тому же функциональному уравнению. Связанная с этим теорема единственности Гельмута Виланда утверждает, что комплексная гамма-функция и ее скалярные кратные являются единственными голоморфными функциями на положительной комплексной полуплоскости, которые подчиняются функциональному уравнению и остаются ограниченными для комплексных чисел с действительной частью от 1 до 2.

Другие сложные функции, которые интерполируют значения факториала, включают гамма-функцию Адамара , которая представляет собой целую функцию для всех комплексных чисел, включая неположительные целые числа. В p -адических числах невозможно непрерывно интерполировать факториальную функцию напрямую, поскольку факториалы больших целых чисел (плотное подмножество p - адических чисел) сходятся к нулю в соответствии с формулой Лежандра, заставляя любую непрерывную функцию, близкую чтобы их значения были равны нулю везде. Вместо этого p -адическая гамма-функция обеспечивает непрерывную интерполяцию модифицированной формы факториала, опуская факторы в факториале, которые делятся на p .

Дигамма -функция представляет собой логарифмическую производную гамма-функции. Так же, как гамма-функция обеспечивает непрерывную интерполяцию факториалов, смещенных на единицу, дигамма-функция обеспечивает непрерывную интерполяцию номеров гармоник , смещенных на константу Эйлера-Машерони .

Вычисление

TI SR-50A , калькулятор 1975 года с факториальной клавишей (третий ряд, в центре справа)

Функция факториала является общей функцией научных калькуляторов . Он также включен в библиотеки научного программирования, такие как Python . модуль математических функций и библиотека Boost C++ . Если эффективность не имеет значения, вычисление факториалов тривиально: просто последовательно умножьте переменную, инициализированную на $1$ целыми числами до $n$. Простота этого вычисления делает его распространенным примером использования различных стилей и методов компьютерного программирования.

Вычисление $n!$ может быть выражено в псевдокоде с использованием итерации как

определить факториал (  n  ): 
    е  := 1 
    для  i  := 1, 2, 3, ...,  n  : 
      ж  :=  ж  *  я 
    вернуть  f 

или используя рекурсию на основе его рекуррентного соотношения как

определить факториал (  n  ): 
    если (  n  = 0) вернуть 1 
    вернуть  n  * факториал (  n  - 1) 
 

Другие методы, подходящие для его вычисления, включают мемоизацию , динамическое программирование , и функциональное программирование . Вычислительную сложность этих алгоритмов можно анализировать с использованием машинной модели вычислений с произвольным доступом с единичной стоимостью , в которой каждая арифметическая операция занимает постоянное время, а каждое число использует постоянный объем памяти. В этой модели эти методы могут вычислять $n!$ во время $O(n)$, а итеративная версия использует пространство $O(1)$. не оптимизирована для хвостовой рекурсии Если рекурсивная версия , для хранения стека вызовов требуется линейное пространство . Однако эта модель вычислений подходит только тогда, когда $n$ достаточно мал, чтобы позволить $n!$ вписаться в машинное слово . Значения 12! и 20! являются крупнейшими факториалами, которые можно хранить соответственно в 32-битном формате . и 64-битные целые числа . Плавающая точка может представлять более крупные факториалы, но приблизительно, а не точно, и все равно будет переполняться для факториалов, превышающих $170!$.

Точное вычисление факториалов большего размера требует арифметики произвольной точности из-за быстрого роста и целочисленного переполнения . Время вычислений можно анализировать как функцию количества цифр или битов в результате. По формуле Стирлинга $n!$ имеет $b=O(n\log n)$ биты. Алгоритм Шенхаге – Штрассена может дать $b$-битный продукт во времени $O(b\log b\log \log b)$, и более быстрые алгоритмы умножения требуют времени $O(b\log b)$ известны. Однако вычисление факториала включает в себя повторяющиеся произведения, а не одно умножение, поэтому эти временные ограничения не применяются напрямую. В этой ситуации вычисление $n!$ умножая числа от 1 до $n$ последовательно неэффективно, поскольку предполагает $n$ умножения, постоянная часть которых занимает время $O(n\log ^{2}n)$ каждый, давая общее время $O(n^{2}\log ^{2}n)$. Лучшим подходом является выполнение умножения в виде алгоритма «разделяй и властвуй» , который умножает последовательность чисел. $i$ числа, разбив его на две подпоследовательности $i/2$числа, умножает каждую подпоследовательность и объединяет результаты с одним последним умножением. Этот подход к факториалу занимает общее время $O(n\log ^{3}n)$: один логарифм получается из количества бит факториала, второй — из алгоритма умножения, а третий — из принципа «разделяй и властвуй».

Еще большую эффективность можно получить, вычислив n ! от его простой факторизации, основанной на том принципе, что возведение в степень путем возведения в квадрат происходит быстрее, чем разложение показателя в произведение. Алгоритм Арнольда Шёнхаге для этого начинается с поиска списка простых чисел до $n$, например, используя решето Эратосфена , и использует формулу Лежандра для вычисления показателя степени для каждого простого числа. Затем он вычисляет произведение степеней простых чисел на эти показатели, используя рекурсивный алгоритм следующим образом:

• Используйте разделяй и властвуй, чтобы вычислить произведение простых чисел, показатели которых нечетны.
• Разделите все показатели степени на два (округлив до целого числа), рекурсивно вычислите произведение простых степеней на эти меньшие показатели степени и возведите результат в квадрат.
• Умножьте результаты двух предыдущих шагов.

Произведение всех простых чисел до $n$ является $O(n)$-битное число по теореме о простых числах , поэтому время для первого шага равно $O(n\log ^{2}n)$, где один логарифм получается из алгоритма «разделяй и властвуй», а другой — из алгоритма умножения. При рекурсивном вызове алгоритма снова можно применить теорему о простых числах, чтобы доказать, что количество битов в соответствующих произведениях уменьшается в постоянном коэффициенте на каждом уровне рекурсии, поэтому общее время этих шагов на всех уровнях рекурсии в геометрический ряд складывает $O(n\log ^{2}n)$. Время возведения в квадрат на втором этапе и умножения на третьем шаге снова равно $O(n\log ^{2}n)$, поскольку каждое из них представляет собой единичное произведение числа на $O(n\log n)$биты. Опять же, на каждом уровне рекурсии задействованные числа имеют постоянную долю от количества битов (потому что в противном случае многократное возведение их в квадрат привело бы к слишком большому конечному результату), поэтому снова количество времени для этих шагов в рекурсивных вызовах добавляется в геометрической прогрессии к $O(n\log ^{2}n)$. Следовательно, весь алгоритм требует времени $O(n\log ^{2}n)$, пропорциональный одному умножению с одинаковым количеством бит в результате.

Связанные последовательности и функции

Основная статья: Список факториальных и биномиальных тем

Несколько других целочисленных последовательностей похожи или связаны с факториалами:

Переменный факториал

Знакомый факториал — это абсолютное значение знакопеременной суммы первых $n$ факториалы, ${\textstyle \sum _{i=1}^{n}(-1)^{n-i}i!}$. Они изучались главным образом в связи с их примитивностью; лишь конечное число из них могут быть простыми, но полный список простых чисел такого вида неизвестен.

Бхаргава факториал

Факториалы Бхаргавы — это семейство целочисленных последовательностей, определенных Манджулом Бхаргавой, с теоретико-числовыми свойствами, аналогичными факториалам, включая сами факториалы как особый случай.

Двойной факториал

Произведение всех нечетных целых чисел с точностью до некоторого нечетного положительного целого числа. $n$ называется двойным факториалом $n$и обозначается $n!!$. То есть,

$$(2k-1)!!=\prod _{i=1}^{k}(2i-1)={\frac {(2k)!}{2^{k}k!}}.$$

Например, 9!! знак равно 1 × 3 × 5 × 7 × 9 = 945 . Двойные факториалы используются в тригонометрических интегралах . в выражениях для гамма-функции в полуцелых числах и объёмах гиперсфер , а также при подсчете бинарных деревьев и полных паросочетаний .

Экспоненциальный факториал

Подобно тому, как треугольные числа суммируют числа из $1$ к $n$, а факториалы берут свое произведение, экспоненциальный факториал возводит в степень. Экспоненциальный факториал определяется рекурсивно как $a_{0}=1,\ a_{n}=n^{a_{n-1}}$. Например, экспоненциальный факториал числа 4 равен

$$4^{3^{2^{1}}}=262144.$$

Эти числа растут гораздо быстрее, чем обычные факториалы.

Падающий факториал

Обозначения $(x)_{n}$ или $x^{\underline {n}}$ иногда используются для обозначения продукта $n$ целые числа со счетом до и включительно $x$, равно $x!/(x-n)!$. Это также известно как падающий факториал или обратный факториал. $(x)_{n}$ обозначение является символом Поххаммера. Падающие факториалы подсчитывают количество различных последовательностей $n$ отдельные предметы, которые можно извлечь из вселенной $x$ предметы. Они встречаются как коэффициенты в высших производных полиномов, и в факториальные моменты величин случайных .

Гиперфакториалы

Гиперфакториал ​ ​ $n$ это продукт $1^{1}\cdot 2^{2}\cdots n^{n}$. Эти числа образуют дискриминанты полиномов Эрмита . Их можно непрерывно интерполировать с помощью К-функции , и подчиняемся аналогам формулы Стирлинга и теорема Вильсона.

Числа Иордании – Полья

Числа Жордана – Полиа представляют собой произведения факториалов, допускающие повторения. Каждое дерево имеет группу симметрии , число симметрий которой является числом Жордана–Пойа, и каждое число Жордана–Пойа подсчитывает симметрии некоторого дерева.

Первобытный

Первобытный ​ $n\#$ является произведением простых чисел, меньших или равных $n$; эта конструкция дает им некоторые свойства делимости, аналогичные факториалам, но в отличие от факториалов они не содержат квадратов . Как и в случае с факториалом простых чисел $n!\pm 1$, исследователи изучили первоначальные простые числа $n\#\pm 1$.

Субфакториал

Субфакториал дает количество нарушений набора $n$объекты. Иногда его обозначают $!n$и равно ближайшему целому числу $n!/e$.

Суперфакториал

Суперфакториал ​ ​ $n$ является продуктом первого $n$факториалы. Суперфакториалы непрерывно интерполируются G-функцией Барнса .

External links

• OEIS sequence A000142 (Factorial numbers)
• "Factorial". Encyclopedia of Mathematics. EMS Press. 2001 [1994].
• Weisstein, Eric W. "Factorial". MathWorld.