Уравнение Сакура – ​​Тетрода

Уравнение Сакура-Тетроде собой выражение энтропии одноатомного идеального представляет газа .

Он назван в честь Хьюго Мартина Тетрода. (1895–1931) и Отто Сакур (1880–1914), который разработал его независимо как решение уравнений статистики газа и энтропии Больцмана примерно в то же время, в 1912 году.

Формула

Уравнение Сакура–Тетроде выражает энтропию $S$ одноатомного идеального газа с точки зрения его термодинамического состояния, в частности, его объема $V$, внутренняя энергия $U$, а число частиц $N$:

${\frac {S}{k_{\rm {B}}N}}=\ln \left[{\frac {V}{N}}\left({\frac {4\pi m}{3h^{2}}}{\frac {U}{N}}\right)^{3/2}\right]+{\frac {5}{2}},$

где $k_{\mathrm {B} }$ — постоянная Больцмана , $m$ - масса частицы газа и $h$ — постоянная Планка .

Уравнение также можно выразить через тепловую длину волны $\Lambda$:

${\frac {S}{k_{\rm {B}}N}}=\ln \left({\frac {V}{N\Lambda ^{3}}}\right)+{\frac {5}{2}},$

Кривые зависимости энтропии от температуры классических и квантовых идеальных газов ( ферми-газ , бозе-газ ) в трех измерениях. Хотя все они находятся в близком согласии при высоких температурах, они расходятся при низких температурах, когда классическая энтропия (уравнение Сакура-Тетроде) начинает приближаться к отрицательным значениям.

Для вывода уравнения Сакура-Тетрода см. Парадокс Гиббса . Об ограничениях, налагаемых на энтропию идеального газа только термодинамикой, см. Статью об идеальном газе .

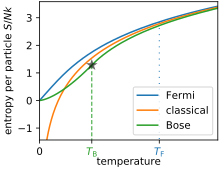
Приведенные выше выражения предполагают, что газ находится в классическом режиме и описывается статистикой Максвелла – Больцмана (с «правильным подсчетом Больцмана»). Из определения тепловой длины волны это означает, что уравнение Сакура – ​​Тетроде справедливо только тогда, когда

${\frac {V}{N\Lambda ^{3}}}\gg 1.$

Энтропия, предсказанная уравнением Сакура-Тетроде, приближается к отрицательной бесконечности, когда температура приближается к нулю.

Константа Сакура – ​​Тетрода

Константа Сакура -Тетрода , обозначаемая / _S0 R , равна S / kBN _, (100 кПа оцененная при температуре Т = 1 кельвин , при стандартном давлении или 101,325 кПа, указать) для моля одного идеальный газ, состоящий из частиц с массой, равной атомной постоянной массы ( m _u = 1,660 539 068 92 (52) × 10 ⁻²⁷  kg кг ). 2018 года CODATA Рекомендуемое значение :

S ₀ / R = −1,151 707 537 06 (45) для p ^тот = 100 кПа

S ₀ / R = −1,164 870 523 58 (45) для p ^тот = 101,325 кПа.

Теоретико-информационная интерпретация

В дополнение к термодинамической перспективе энтропии , инструменты теории информации могут быть использованы для обеспечения информационной перспективы энтропии . В частности, можно вывести уравнение Сакура – ​​Тетроде в терминах теории информации. Общая энтропия представлена ​​как сумма четырех отдельных энтропий, т. е. четырех различных источников недостающей информации. Это позиционная неопределенность, неопределенность импульса, квантовомеханический принцип неопределенности и неразличимость частиц. Суммируя четыре части, уравнение Сакура – ​​Тетрода задается следующим образом:

${\begin{aligned}{\frac {S}{k_{\rm {B}}N}}&=[\ln V]+\left[{\frac {3}{2}}\ln \left(2\pi emk_{\rm {B}}T\right)\right]+[-3\ln h]+\left[-{\frac {\ln N!}{N}}\right]\\&\approx \ln \left[{\frac {V}{N}}\left({\frac {2\pi mk_{\rm {B}}T}{h^{2}}}\right)^{\frac {3}{2}}\right]+{\frac {5}{2}}\end{aligned}}$

При выводе используется приближение Стирлинга : $\ln N!\approx N\ln N-N$. Строго говоря, использование размерных аргументов логарифмов неверно, однако их использование представляет собой «сокращение», созданное для простоты. Если бы каждый логарифмический аргумент был разделен на неопределенную стандартную величину, выраженную через неопределенную стандартную массу, длину и время, эти стандартные значения сократились бы в конечном результате, что привело бы к тому же выводу. Отдельные члены энтропии не будут абсолютными, а скорее будут зависеть от выбранных стандартов и будут различаться в зависимости от разных стандартов на аддитивную константу.

Дальнейшее чтение

• Эмч, Г.Г.; Лю, К. (2002), Логика термостатистической физики , Springer-Verlag , Глава 3: Кинетическая теория газов .
• Куцояннис, Д. (2013), «Физика неопределенности, парадокс Гиббса и неразличимые частицы», Исследования по истории и философии науки, часть B , 44 (4): 480–489, Бибкод : 2013SHPMP..44..480K , дои : 10.1016/ж.шпсб.2013.08.007 . (При этом уравнение Сакура – ​​Тетроде выводится другим способом, также на основе информации.)
• Паньос, Ф.Дж.; Перес, Э. (2015), «Уравнение Сакура–Тетрода в лаборатории», European Journal of Physics , 36 (5): 055033, Bibcode : 2015EJPh...36e5033J , doi : 10.1088/0143-0807/36/5/ 055033 , S2CID   124422176 .
• Уильямс, Ричард (2009), «Уравнение Сакура – ​​Тетрода: как энтропия встретила квантовую механику» , APS News , 18 (8) .