✖


Jump to content

Силовое поле (химия)

Чтобы узнать о других значениях, см. Поле силы .
Часть силового поля этана для тянущейся связи CC.

В контексте химии , молекулярной физики , физической химии и молекулярного моделирования силовое поле — это вычислительная модель, которая используется для описания сил между атомами (или совокупностями атомов) внутри молекул или между молекулами, а также в кристаллах. Силовые поля представляют собой разновидность межатомных потенциалов . Точнее, силовое поле относится к функциональной форме и наборам параметров, используемых для расчета потенциальной энергии системы на атомистическом уровне. Силовые поля обычно используются в молекулярной динамике или моделировании Монте-Карло . Параметры выбранной энергетической функции могут быть получены из данных классического лабораторного эксперимента, расчетов по квантовой механике или того и другого. Силовые поля используют ту же концепцию, что и силовые поля в классической физике , с основным отличием в том, что параметры силового поля в химии описывают энергетический ландшафт на атомистическом уровне. Из силового поля действующие силы на каждую частицу определяются как градиент потенциальной энергии по отношению к координатам частицы. [1]

Сегодня существует большое количество различных типов силовых полей (например, для органических молекул , ионов , полимеров , минералов и металлов ). В зависимости от материала для силовых полей обычно выбираются разные функциональные формы, поскольку в поведении материала доминируют разные типы атомистических взаимодействий.

Существуют различные критерии, которые можно использовать для классификации стратегий параметризации силового поля. Важным отличием является «специфичность компонента» и «переносимость». При параметризации конкретного компонента рассматриваемое силовое поле разрабатывается исключительно для описания одного данного вещества (например, воды). [2] Для переносимого силового поля все или некоторые параметры спроектированы как строительные блоки и становятся переносимыми/применимыми для различных веществ (например, метильные группы в алкановых переносимых силовых полях). [3] Еще одно важное отличие касается физической структуры моделей: силовые поля всех атомов предоставляют параметры для каждого типа атомов в системе, включая водород , в то время как межатомные потенциалы объединенных атомов рассматривают атомы водорода и углерода в метильных группах и метиленовых мостиках. как один центр взаимодействия. [4] [5] Грубозернистые потенциалы, которые часто используются при долговременном моделировании макромолекул, таких как белки , нуклеиновые кислоты и многокомпонентные комплексы, приносят в жертву химические детали ради более высокой эффективности вычислений. [6]

Силовые поля для молекулярных систем [ править ]

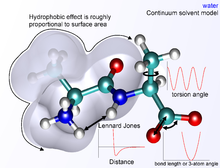
Функция потенциальной энергии молекулярной механики с континуальным растворителем.

Основная функциональная форма потенциальной энергии для моделирования молекулярных систем включает члены внутримолекулярного взаимодействия для взаимодействий атомов, которые связаны ковалентными связями , и межмолекулярные (т.е. несвязанные, также называемые нековалентными ) члены, которые описывают дальнодействующие электростатические силы и силы Ван-дер-Ваальса . Конкретное разложение членов зависит от силового поля, но общий вид полной энергии в аддитивном силовом поле можно записать как

где компоненты ковалентного и нековалентного вклада определяются следующим суммированием:

Члены связи и угла обычно моделируются квадратичными энергетическими функциями, которые не допускают разрыва связи. Более реалистичное описание ковалентной связи при более высоком растяжении дает более дорогой потенциал Морзе . Функциональная форма двугранной энергии варьируется от одного силового поля к другому. Могут быть добавлены дополнительные «неподходящие крутильные» члены для обеспечения плоскостности ароматических колец и других сопряженных систем , а также «перекрестные члены», которые описывают связь различных внутренних переменных, таких как углы и длины связей. Некоторые силовые поля также включают явные условия для водородных связей .

Несвязанные члены являются наиболее трудоемкими в вычислительном отношении. Популярный выбор — ограничить взаимодействие парными энергиями. Член Ван-дер-Ваальса обычно вычисляется с использованием потенциала Леннарда-Джонса. [7] или потенциал Ми [8] и электростатический член с законом Кулона . Однако оба могут быть буферизованы или масштабированы с помощью постоянного коэффициента для учета электронной поляризуемости . Большое количество силовых полей, основанных на этом или подобных выражениях энергии, было предложено в последние десятилетия для моделирования различных типов материалов, таких как молекулярные вещества, металлы, стекла и т. д. - полный список силовых полей см. ниже.

Растяжка облигаций [ править ]

Поскольку облигации редко значительно отклоняются от своей равновесной стоимости, в наиболее упрощенных подходах используется формула закона Гука :

где - силовая постоянная, длина связи, а - значение длины связи между атомами и когда все остальные члены силового поля равны 0. Член иногда по-разному определяется или принимается в разных термодинамических условиях.

Константа растяжения связи может быть определен на основе экспериментального инфракрасного спектра, спектра комбинационного рассеяния света или квантово-механических расчетов высокого уровня. [4] Константа определяет частоты колебаний при моделировании молекулярной динамики . Чем сильнее связь между атомами, тем выше значение силовой постоянной и тем выше волновое число (энергия) в ИК/КР спектре.

Хотя формула закона Гука обеспечивает разумный уровень точности при длинах связей вблизи равновесного расстояния, она становится менее точной по мере удаления. Чтобы лучше смоделировать кривую Морса, можно использовать кубические и более высокие степени. [4] [9] Однако для большинства практических приложений эти различия незначительны, а неточности в предсказаниях длин связей составляют порядка тысячных ангстрем, что также является пределом надежности для обычных силовых полей. Вместо этого можно использовать потенциал Морзе , чтобы обеспечить разрыв связей и повысить точность, хотя его вычисления менее эффективны. Для реактивных силовых полей дополнительно учитываются разрыв связи и порядок связи.

Электростатические взаимодействия [ править ]

Электростатические взаимодействия представлены кулоновской энергией, которая использует заряды атомов. для представления химической связи в диапазоне от ковалентной до полярной ковалентной и ионной связи . Типичной формулой является закон Кулона :

где это расстояние между двумя атомами и . Полная кулоновская энергия представляет собой сумму по всем парным комбинациям атомов и обычно исключает 1, 2 связанных атома, 1, 3 связанных атома, а также 1, 4 связанных атома. [ объяснить ] . [10] [11] [12]

Атомные заряды могут вносить доминирующий вклад в потенциальную энергию, особенно для полярных молекул и ионных соединений, и имеют решающее значение для моделирования геометрии, энергии взаимодействия и реакционной способности. При назначении сборов обычно используется эвристический подход с различными возможными решениями.

Силовые поля для кристаллических систем [ править ]

Атомистические взаимодействия в кристаллических системах существенно отличаются от взаимодействий в молекулярных системах. [13] например, органических молекул. Для кристаллических систем, в частности, важны взаимодействия многих тел, и ими нельзя пренебрегать, если целью является высокая точность силового поля. Для кристаллических систем с ковалентной связью потенциалы порядка связей , например потенциалы Терсоффа. обычно используют [14] Для металлических систем обычно используются встроенные атомные потенциалы. [15] [16] используются. также так называемые модельные потенциалы Друде . Для металлов разработаны [17] которые описывают форму прикрепления электронов к ядрам. [18] [19]

Параметризация [ править ]

Помимо функциональной формы потенциалов, силовое поле состоит из параметров этих функций. Вместе они определяют взаимодействия на атомистическом уровне. Параметризация, то есть определение значений параметров, имеет решающее значение для точности и надежности силового поля. Для параметризации различных веществ, например металлов, ионов и молекул, были разработаны различные процедуры параметризации. Для разных типов материалов обычно используются разные стратегии параметризации. В общем, можно выделить два основных типа параметризации: либо использование данных/информации с атомистического уровня, например, из квантово-механических расчетов или спектроскопических данных, либо использование данных из макроскопических свойств, например, твердости или сжимаемости данного материала. Часто используется комбинация этих маршрутов. Следовательно, так или иначе, параметры силового поля всегда определяются эмпирическим путем. Тем не менее, термин «эмпирический» часто используется в контексте параметров силового поля, когда для подгонки использовались макроскопические данные о свойствах материала. Экспериментальные данные (микроскопические и макроскопические), включенные в подборку, например энтальпия испарения , энтальпия сублимации . , дипольные моменты и различные спектроскопические свойства, такие как частоты колебаний [20] [9] [21] Часто для молекулярных систем квантово-механические расчеты в газовой фазе используются для параметризации внутримолекулярных взаимодействий и параметризации межмолекулярных дисперсионных взаимодействий с использованием макроскопических свойств, таких как плотности жидкости. [3] [22] [23] Присвоение атомных зарядов часто следует квантовомеханическим протоколам с некоторыми эвристиками, что может привести к значительным отклонениям в представлении конкретных свойств. [24] [25] [26]

За последние десятилетия было использовано большое количество рабочих процессов и процедур параметризации с использованием различных данных и стратегий оптимизации для определения параметров силового поля. Они существенно различаются, что также связано с разной направленностью разных разработок. Параметры молекулярного моделирования биологических макромолекул, таких как белки , ДНК и РНК, часто были получены/перенесены из наблюдений за небольшими органическими молекулами , которые более доступны для экспериментальных исследований и квантовых расчетов.

Типы атомов определены для разных элементов, а также для одних и тех же элементов в достаточно разных химических средах. Например, кислорода атомы в воде и атомы кислорода в карбонильной функциональной группе классифицируются как разные типы силового поля. [21] Типичные наборы параметров молекулярного силового поля включают значения атомной массы , атомного заряда , параметров Леннарда-Джонса для каждого типа атома, а также равновесные значения длин связей , валентных углов и двугранных углов . [27] Связанные термины относятся к парам, тройкам и четверкам связанных атомов и включают значения эффективной пружинной жесткости для каждого потенциала.

Эвристические процедуры параметризации силового поля очень успешно применялись в течение многих лет, но недавно подверглись критике. [28] [29] поскольку они, как правило, не полностью автоматизированы и поэтому подвержены некоторому субъективизму разработчиков, что также приносит проблемы с воспроизводимостью процедуры параметризации.

Усилия по предоставлению открытых исходных кодов и методов включают openMM и openMD . Использование полуавтоматизации или полной автоматизации без учета химических знаний, вероятно, приведет к увеличению несоответствий на уровне атомных зарядов при назначении остальных параметров и, вероятно, ухудшит интерпретируемость и эффективность параметров.

Базы данных силовых полей [ править ]

За последние десятилетия было опубликовано большое количество работ о силовых полях – в основном в научных изданиях. В последние годы некоторые базы данных пытались собрать, классифицировать и сделать силовые поля доступными в цифровом виде. При этом разные базы данных фокусируются на разных типах силовых полей. Например, база данных openKim фокусируется на межатомных функциях, описывающих отдельные взаимодействия между конкретными элементами. [30] База данных TraPPE фокусируется на переносимых силовых полях органических молекул (разработанных группой Siepmann). [31] База данных MolMod фокусируется на молекулярных и ионных силовых полях (как специфических для компонентов, так и переносимых). [5] [32]

Типы функций переносимости и смешивания [ править ]

Функциональные формы и наборы параметров определены разработчиками межатомных потенциалов и обладают различной степенью самосогласованности и переносимости. Когда функциональные формы потенциальных членов изменяются или смешиваются, параметры одной межатомной потенциальной функции обычно не могут использоваться вместе с другой межатомной потенциальной функцией. [33] В некоторых случаях модификации можно внести с небольшими усилиями, например, с потенциалов Леннарда-Джонса 9-6 на потенциалы Леннарда-Джонса 12-6. [12] Переход от потенциалов Букингема к гармоническим потенциалам или от встроенных моделей атома к гармоническим потенциалам, напротив, потребует множества дополнительных предположений и может оказаться невозможным.

Во многих случаях силовые поля можно напрямую комбинировать. Однако зачастую требуются дополнительные спецификации и предположения.

Ограничения [ править ]

Все межатомные потенциалы основаны на приближениях и экспериментальных данных, поэтому их часто называют эмпирическими . Производительность варьируется от более высокой точности, чем при расчетах теории функционала плотности (DFT), с доступом к системам и временным масштабам в миллионы раз большего размера, до случайных предположений в зависимости от силового поля. [34] Использование точных представлений о химической связи в сочетании с воспроизводимыми экспериментальными данными и проверкой может привести к созданию устойчивых межатомных потенциалов высокого качества с гораздо меньшим количеством параметров и допущений по сравнению с квантовыми методами на уровне ДПФ. [35] [36]

Возможные ограничения включают атомные заряды, также называемые точечными зарядами. Большинство силовых полей полагаются на точечные заряды для воспроизведения электростатического потенциала вокруг молекул, что хуже работает при анизотропном распределении зарядов. [37] Средство правовой защиты состоит в том, чтобы точечные обвинения имели четкое толкование. [26] и виртуальные электроны могут быть добавлены, чтобы уловить существенные особенности электронной структуры, такие как дополнительная поляризуемость в металлических системах для описания потенциала изображения, внутренние мультипольные моменты в π-сопряженных системах и неподеленные пары в воде. [38] [39] [40] Электронную поляризацию окружающей среды можно лучше учесть, используя поляризуемые силовые поля. [41] [42] или используя макроскопическую диэлектрическую проницаемость . Однако применение одного значения диэлектрической проницаемости является грубым приближением в сильно гетерогенной среде белков, биологических мембран, минералов или электролитов. [43]

Все типы сил Ван-дер-Ваальса также сильно зависят от окружающей среды, поскольку эти силы возникают в результате взаимодействия индуцированных и «мгновенных» диполей (см. Межмолекулярные силы ). Оригинальная теория этих сил Фрица Лондона применима только в вакууме. Более общая теория сил Ван дер Ваальса в конденсированных средах была разработана А. Д. Маклахланом в 1963 году и включала в качестве частного случая оригинальный подход Лондона. [44] Теория Маклахлана предсказывает, что притяжение Ван-дер-Ваальса в средах слабее, чем в вакууме, и подчиняется правилу «подобное растворяется подобное» , что означает, что разные типы атомов взаимодействуют слабее, чем одинаковые типы атомов. [45] Это контрастирует с комбинаторными правилами или уравнением Слейтера-Кирквуда, применяемыми для разработки классических силовых полей. Комбинаторные правила утверждают, что энергия взаимодействия двух разнородных атомов (например, C...N) представляет собой среднее значение энергий взаимодействия соответствующих идентичных пар атомов (т.е. C...C и N...N). Согласно теории Маклахлана, взаимодействия частиц в средах могут быть даже полностью отталкивающими, как это наблюдается для жидкого гелия . [44] однако отсутствие испарения и наличие точки замерзания противоречит теории чисто отталкивающих взаимодействий. Измерения сил притяжения между различными материалами ( постоянная Гамакера ) были объяснены Якобом Исраелачвили . [44] Например, « взаимодействие между углеводородами в воде составляет около 10% от взаимодействия в вакууме ». [44] Такие эффекты представлены в молекулярной динамике посредством парных взаимодействий, которые пространственно более плотны в конденсированной фазе по сравнению с газовой фазой и воспроизводятся после проверки параметров для всех фаз для воспроизведения химической связи, плотности и энергии сцепления/поверхности.

Ограничения были сильно ощутимы в уточнении структуры белка. Основная проблема заключается в огромном конформационном пространстве полимерных молекул, которое выходит за рамки нынешних вычислительных возможностей, когда они содержат более ~20 мономеров. [46] Участники проекта « Критическая оценка прогнозирования структуры белка» (CASP) не пытались усовершенствовать свои модели, чтобы избежать « центрального затруднения молекулярной механики, а именно того, что минимизация энергии или молекулярная динамика обычно приводят к модели, которая меньше похожа на экспериментальную структуру ». [47] Силовые поля успешно применяются для уточнения структуры белков в различных приложениях рентгеновской кристаллографии и ЯМР-спектроскопии , особенно с использованием программы XPLOR. [48] Однако уточнение обусловлено главным образом набором экспериментальных ограничений, а межатомные потенциалы служат главным образом для устранения межатомных препятствий. Результаты расчетов практически не отличались от потенциалов жестких сфер, реализованных в программе DYANA. [49] (расчеты по данным ЯМР) или с помощью программ кристаллографического уточнения, вообще не использующих энергетических функций. Эти недостатки связаны с межатомными потенциалами и невозможностью эффективно исследовать конформационное пространство больших молекул. [50] Таким образом, разработка параметров для решения таких крупномасштабных проблем требует новых подходов. Особой проблемной областью является моделирование гомологии белков. [51] были разработаны альтернативные эмпирические оценочные функции Между тем, для докинга лигандов . [52] сворачивание белка , [53] [54] [55] уточнение модели гомологии, [56] вычислительный дизайн белка , [57] [58] [59] и моделирование белков в мембранах. [60]

Также утверждалось, что некоторые силовые поля белков действуют с энергиями, не имеющими отношения к сворачиванию белков или связыванию лигандов. [41] Параметры силовых полей белков воспроизводят энтальпию сублимации , т. е . энергию испарения молекулярных кристаллов. Однако сворачивание белка и связывание лиганда термодинамически ближе к кристаллизации или переходам жидкость-твердое тело, поскольку эти процессы представляют собой замораживание мобильных молекул в конденсированной среде. [61] [62] [63] Таким образом, ожидается, что изменения свободной энергии во время сворачивания белка или связывания лиганда представляют собой комбинацию энергии, подобной теплоте плавления (энергии, поглощаемой при плавлении молекулярных кристаллов), вклада конформационной энтропии и сольватации свободной энергии . Теплота плавления значительно меньше энтальпии сублимации. [44] Следовательно, потенциалы, описывающие сворачивание белка или связывание лиганда, требуют более последовательных протоколов параметризации, например, как описано для IFF. Действительно, энергии Н-связей в белках составляют ~ -1,5 ккал/моль, если оценивать их с помощью белковой инженерии или от альфа-спирали к клубку . данных о переходе [64] [65] но те же энергии, оцененные по сублимации энтальпии молекулярных кристаллов, составляли от -4 до -6 ккал/моль, [66] что связано с переформированием существующих водородных связей, а не с образованием водородных связей с нуля. Глубина модифицированных потенциалов Леннарда-Джонса, полученных на основе данных белковой инженерии, также была меньше, чем у типичных потенциальных параметров, и подчинялась правилу «подобное растворяется подобное» , как предсказывает теория Маклахлана. [41]

Силовые поля доступны в литературе [ править ]

Дополнительная информация: Сравнение реализаций силового поля , Программное обеспечение для молекулярного проектирования и Сравнение программного обеспечения для моделирования молекулярной механики.

Различные силовые поля предназначены для разных целей:

Классический [ править ]

  • ЯНТАРЬ (Вспомогательное построение моделей и уточнение энергии) – широко используется для белков и ДНК.
  • CFF (Consistent Force Field) — семейство силовых полей, адаптированных к широкому спектру органических соединений, включает силовые поля для полимеров, металлов и т. д. CFF был разработан Арье Варшелем , Лифсоном и его коллегами как общий метод для объединения исследований энергии, структуры и вибрации обычных молекул и молекулярных кристаллов. Программа CFF, разработанная Левиттом и Уоршелом, основана на декартовом представлении всех атомов и послужила основой для многих последующих программ моделирования.
  • CHARMM (химия в Гарвардской молекулярной механике) - первоначально разработан в Гарварде, широко используется как для малых молекул, так и для макромолекул.
  • КОСМОС-ЯМР - гибридное силовое поле КМ/ММ, адаптированное к различным неорганическим соединениям, органическим соединениям и биологическим макромолекулам, включая полуэмпирический расчет свойств атомных зарядов ЯМР. COSMOS-NMR оптимизирован для объяснения структуры на основе ЯМР и реализован в пакете молекулярного моделирования COSMOS. [67]
  • CVFF – также широко используется для малых молекул и макромолекул. [21]
  • ЕСЭПП [68] – первое силовое поле для полипептидных молекул – разработанное Ф.А. Момани, Х.А. Шерагой и коллегами. [69] [70] ECEPP был разработан специально для моделирования пептидов и белков. Он использует фиксированную геометрию аминокислотных остатков для упрощения поверхности потенциальной энергии. Таким образом, минимизация энергии осуществляется в пространстве торсионных углов белка. И MM2, и ECEPP включают потенциалы для H-связей и торсионные потенциалы для описания вращений вокруг одинарных связей. ECEPP/3 был реализован (с некоторыми изменениями) в Механике внутренних координат и FANTOM. [71]
  • GROMOS (GROningen MOlecular Simulation) – силовое поле, входящее в состав программного обеспечения GROMOS, универсального пакета компьютерного моделирования молекулярной динамики для изучения биомолекулярных систем. [72] Силовое поле GROMOS A-версия было разработано для применения к водным или аполярным растворам белков, нуклеотидов и сахаров. Также доступна B-версия для моделирования изолированных молекул в газовой фазе.
  • IFF (Interface Force Field) – охватывает металлы, минералы, 2D-материалы и полимеры. Он использует 12-6 ЖЖ и 9-6 ЖЖ-взаимодействий. [73] [74] IFF был разработан для соединений всей таблицы Менделеева. Он присваивает постоянные заряды, использует стандартные условия в качестве эталонного состояния, воспроизводит структуры, энергии и производные энергии, а также количественно определяет ограничения для всех включенных соединений. [73] [75] ( Силовое поле интерфейса IFF) предполагает одно выражение энергии для всех соединений в периоде (с вариантами 9-6 и 12-6 LJ). IFF в большинстве случаев неполяризуется, но также включает поляризуемые части, например, для некоторых металлов (Au, W) и пи-сопряженных молекул. [76] [40] [39]
  • MMFF ( Merk Molecular Force Field ) – разработано в компании Merck для широкого спектра молекул.
  • MM2 был разработан Норманом Аллинджером главным образом для конформационного анализа углеводородов и других небольших органических молекул. Он предназначен для максимально точного воспроизведения равновесной ковалентной геометрии молекул. Он реализует большой набор параметров, который постоянно уточняется и обновляется для многих различных классов органических соединений (ММ3 и ММ4). [77] [78] [79] [80] [81]
  • OPLS (Оптимизированный потенциал для моделирования жидкостей) (варианты включают OPLS-AA, OPLS-UA, OPLS-2001, OPLS-2005, OPLS3e, OPLS4) – разработан Уильямом Л. Йоргенсеном на химическом факультете Йельского университета.
  • QCFF/PI – общие силовые поля для сопряженных молекул. [82] [83]
  • UFF (Универсальное силовое поле) – общее силовое поле с параметрами для всей таблицы Менделеева, включая актиноиды, разработанное в Университете штата Колорадо. [84] Известно, что надежность низкая из-за отсутствия проверки и интерпретации параметров практически для всех заявленных соединений, особенно металлов и неорганических соединений. [85] [75]

Поляризуемый [ править ]

Несколько силовых полей явно фиксируют поляризуемость , при которой на эффективный заряд частицы могут влиять электростатические взаимодействия с ее соседями. Распространены модели ядро-оболочка, которые состоят из положительно заряженной частицы ядра, представляющей поляризуемый атом, и отрицательно заряженной частицы, прикрепленной к атому ядра через пружинный потенциал гармонического осциллятора . [86] [87] [88] Недавние примеры включают поляризуемые модели с виртуальными электронами, которые воспроизводят заряды изображений в металлах. [76] и поляризуемые биомолекулярные силовые поля. [89]

  • ЯНТАРЬ – поляризуемое силовое поле, разработанное Джимом Колдуэллом и его коллегами. [90]
  • AMOEBA (Атомно-мультипольная оптимизированная энергетика для биомолекулярных применений) – силовое поле, разработанное Пэнъю Реном (Техасский университет в Остине) и Джеем В. Пондером (Вашингтонский университет). [91] Силовое поле AMOEBA постепенно переходит в более насыщенную физикой AMOEBA+. [92] [93]
  • CHARMM – поляризуемое силовое поле, разработанное С. Пателем (Университет штата Делавэр) и К. Л. Бруксом III (Университет Мичигана). [89] [94] Основан на классическом генераторе Друде, разработанном Александром МакКереллом (Университет Мэриленда, Балтимор) и Бенуа Ру (Университет Чикаго). [95] [96]
  • CFF/ind и ENZYMIX – первое поляризуемое силовое поле [97] который впоследствии использовался во многих приложениях к биологическим системам. [42]
  • КОСМОС-ЯМР (компьютерное моделирование молекулярной структуры) – разработан Ульрихом Штернбергом и его коллегами. Гибридное силовое поле QM/MM позволяет выполнить явный квантово-механический расчет электростатических свойств с использованием локализованных орбиталей связей с формализмом быстрого BPT. [98] Флуктуации заряда атомов возможны на каждом этапе молекулярной динамики.
  • DRF90 – разработан П.Т. ван Дуйнен и его коллеги. [99]
  • NEMO (Неэмпирическая молекулярная орбиталь) – процедура, разработанная Гуннаром Карлстремом и его коллегами из Лундского университета (Швеция). [100]
  • PIPF - Поляризуемый межмолекулярный потенциал для жидкостей представляет собой индуцированное точечно-дипольное силовое поле для органических жидкостей и биополимеров. Молекулярная поляризация основана на модели взаимодействующего диполя Толе (TID) и была разработана исследовательской группой Цзяли Гао Гао | в Университете Миннесоты. [101] [102]
  • Поляризуемое силовое поле (PFF) – разработано Ричардом А. Фриснером и его коллегами. [103]
  • Уравнивание химического потенциала на основе SP (CPE) – подход, разработанный Р. Челли и П. Прокаччи. [104]
  • PHAST – поляризуемый потенциал, разработанный Крисом Сиосе и его коллегами. [105]
  • ORIENT – процедура, разработанная Энтони Дж. Стоуном (Кембриджский университет) и его сотрудниками. [106]
  • Гауссова электростатическая модель (GEM) – поляризуемое силовое поле, основанное на аппроксимации плотности, разработанное Томасом А. Дарденом и Г. Андресом Сиснеросом в NIEHS; и Жан-Филипп Пикемаль из Университета Париж VI. [107] [108] [109]
  • Атомистический поляризуемый потенциал для жидкостей, электролитов и полимеров (APPLE&P), разработанный Олегом Борогиным, Дмитрием Бедровым и его коллегами и распространяемый компанией Wasatch Molecular Incorporated. [110]
  • Поляризационная процедура, основанная на подходе Кима-Гордона, разработанном Юргом Хуттером и его коллегами (Университет Цюриха). [ нужна ссылка ]
  • GFN-FF (силовое поле геометрии, частоты и нековалентного взаимодействия) - полностью автоматизированное частично поляризуемое общее силовое поле для точного описания структур и динамики больших молекул в периодической таблице, разработанное Стефаном Гримме и Себастьяном Шпихером в университете. Бонна. [111]
  • WASABe v1.0 PFF (для воды, органических растворителей и аккумуляторных электролитов) Изотропное атомно-дипольное поляризуемое силовое поле для точного описания аккумуляторных электролитов с точки зрения термодинамических и динамических свойств при высоких концентрациях солей лития в сульфонатном растворителе Олег Старовойтов [112]

Реактивный [ править ]

  • EVB ( Эмпирическая валентная связь ) – поле реактивной силы, введенное Уоршелем и его коллегами для использования при моделировании химических реакций в различных средах. EVB облегчает расчет свободной энергии активации в конденсированных фазах и ферментах .
  • ReaxFF – поле реактивной силы (межатомный потенциал), разработанное Адри ван Дуином, Уильямом Годдардом и его коллегами. Он медленнее, чем классический MD (50x), требует наборов параметров со специальной проверкой и не имеет проверки для поверхностной и межфазной энергий. Параметры неинтерпретируемы. Можно использовать динамическое моделирование химических реакций в атомистическом масштабе. [113] Параллелизованный ReaxFF позволяет проводить реактивное моделирование >>1 000 000 атомов на больших суперкомпьютерах.

Крупнозернистый [ править ]

  • DPD ( динамика диссипативных частиц ) — это метод, обычно применяемый в химической технологии. Обычно он используется для изучения гидродинамики различных простых и сложных жидкостей, которые требуют рассмотрения масштабов времени и длины, больших, чем те, которые доступны классической молекулярной динамике . Потенциал был первоначально предложен Хугербрюгге и Кельманом. [114] [115] с более поздними модификациями Эспаньола и Уоррена [116] Текущее состояние дел было хорошо документировано на семинаре CECAM в 2008 году. [117] Недавно была предпринята работа по включению некоторых химических субтитров, имеющих отношение к растворам. Это привело к работе по рассмотрению автоматической параметризации потенциалов взаимодействия DPD с экспериментальными наблюдаемыми. [29]
  • МАРТИНИ — крупнозернистый потенциал, разработанный Марринком и его коллегами из Университета Гронингена , первоначально разработанный для молекулярно-динамического моделирования липидов. [6] позже распространился на различные другие молекулы. Силовое поле применяет отображение четырех тяжелых атомов к одному месту взаимодействия CG и параметризуется с целью воспроизведения термодинамических свойств.
  • SAFT – нисходящая крупнозернистая модель, разработанная группой молекулярной системной инженерии Имперского колледжа Лондона, адаптированная к плотности жидкой фазы и давлению паров чистых соединений с использованием уравнения состояния SAFT. [118]
  • SIRAH – крупнозернистое силовое поле, разработанное Пантано и его коллегами из Группы биомолекулярного моделирования Института Пастера в Монтевидео, Уругвай; разработан для молекулярной динамики воды, ДНК и белков. Доступно бесплатно для пакетов AMBER и GROMACS.
  • VAMM (молекулярная механика виртуального атома) - крупнозернистое силовое поле, разработанное Коркутом и Хендриксоном для расчетов молекулярной механики, таких как крупномасштабные конформационные переходы, основанные на виртуальных взаимодействиях атомов C-альфа. Это силовое поле, основанное на знаниях и созданное для выявления особенностей, зависящих от вторичной структуры и контактной информации, специфичной для остатков в белках. [119]

Машинное обучение [ править ]

  • MACE (Multi Atomic Cluster Expansion) — это высокоточная архитектура силового поля машинного обучения, которая сочетает в себе строгое многочастичное расширение полной потенциальной энергии с вращательно-эквивариантными представлениями системы. [120]
  • ANI (искусственный узкий интеллект) — это передаваемый потенциал нейронной сети, построенный на основе атомарных векторов окружающей среды и способный обеспечить точность ДПФ с точки зрения энергии. [121]
  • FFLUX (первоначально QCTFF) [122] Набор обученных моделей кригинга , которые работают вместе, чтобы создать молекулярное силовое поле, обученное атомам в молекулах или энергетическим терминам квантово-химической топологии, включая электростатику, обмен и электронную корреляцию. [123] [124]
  • TensorMol, смешанная модель, нейронная сеть обеспечивает потенциал ближнего действия, в то время как более традиционные потенциалы добавляют экранированные условия дальнего действия.
  • Δ-ML - это не метод силового поля, а модель, которая добавляет изученные поправочные энергетические термины к приближенным и относительно дешевым в вычислительном отношении квантово-химическим методам, чтобы обеспечить уровень точности квантово-химической модели более высокого порядка и более дорогой в вычислительном отношении. [125]
  • SchNet — нейронная сеть , использующая сверточные слои с непрерывной фильтрацией для прогнозирования химических свойств и поверхностей потенциальной энергии. [126]
  • PhysNet — это энергетическая функция на основе нейронной сети для прогнозирования энергии, сил и (колебающихся) частичных зарядов. [127]

Вода [ править ]

Основная статья: Водная модель

Набор параметров, используемых для моделирования воды или водных растворов (по сути, силовое поле для воды), называется моделью воды . Было предложено множество водных моделей; [5] некоторые примеры: TIP3P, TIP4P, [2] SPC, гибкая модель простой точечной подпитки воды (гибкий SPC), ST2 и мВт. [128] Другие растворители и методы представления растворителей также применяются в вычислительной химии и физике; они называются моделями растворителей .

Модифицированные аминокислоты [ править ]

  • Forcefield_PTM – силовое поле и веб-инструмент на основе AMBER для моделирования распространенных посттрансляционных модификаций аминокислот в белках, разработанные Крисом Флудасом и его коллегами. Он использует модель заряда ff03 и имеет несколько поправок кручения боковой цепи, параметризованных так, чтобы соответствовать квантово-химической вращающейся поверхности. [129]
  • Forcefield_NCAA — силовое поле и веб-инструмент на основе AMBER для моделирования распространенных неприродных аминокислот в белках в конденсированной фазе с использованием модели заряда ff03. [130] Сообщается, что заряды коррелируют с энергией свободной гидратации соответствующих аналогов боковой цепи. [131]

Другое [ править ]

См. также [ править ]

Ссылки [ править ]

  1. ^ Френкель Д. (2007). Понимание молекулярного моделирования: от алгоритмов к приложениям . Академическая пресса. ISBN  978-0-12-267351-1 . OCLC   254835355 .
  2. ↑ Перейти обратно: Перейти обратно: а б Абаскаль Дж.Л., Вега С (декабрь 2005 г.). «Общая модель конденсированных фаз воды: TIP4P/2005». Журнал химической физики . 123 (23): 234505. Бибкод : 2005JChPh.123w4505A . дои : 10.1063/1.2121687 . ПМИД   16392929 . S2CID   9757894 .
  3. ↑ Перейти обратно: Перейти обратно: а б Сиу С.В., Плугачкова К., Бёкманн Р.А. (апрель 2012 г.). «Оптимизация силового поля ОПЛС-АА для длинных углеводородов». Журнал химической теории и вычислений . 8 (4): 1459–70. дои : 10.1021/ct200908r . ПМИД   26596756 .
  4. ↑ Перейти обратно: Перейти обратно: а б с Лич А (30 января 2001 г.). Молекулярное моделирование: принципы и приложения (2-е изд.). Харлоу: Прентис Холл. ISBN  9780582382107 .
  5. ↑ Перейти обратно: Перейти обратно: а б с Стефан, Саймон; Хорш, Мартин Т.; Врабец, Ядран; Хассе, Ганс (3 июля 2019 г.). «MolMod – база данных силовых полей с открытым доступом для молекулярного моделирования жидкостей» . Молекулярное моделирование . 45 (10): 806–814. arXiv : 1904.05206 . дои : 10.1080/08927022.2019.1601191 . ISSN   0892-7022 . S2CID   119199372 .
  6. ↑ Перейти обратно: Перейти обратно: а б Марринк С.Дж., Рисселада Х.Дж., Ефимов С., Тилеман Д.П., де Врис А.Х. (июль 2007 г.). «Силовое поле МАРТИНИ: крупнозернистая модель для биомолекулярного моделирования» (PDF) . Журнал физической химии Б. 111 (27): 7812–24. дои : 10.1021/jp071097f . ПМИД   17569554 . S2CID   13874240 .
  7. ^ Ленхард, Йоханнес; Стефан, Саймон; Хассе, Ганс (февраль 2024 г.). «Дитя предсказания. Об истории, онтологии и вычислениях Леннарда-Джонезиума» . Исследования по истории и философии науки . 103 : 105–113. дои : 10.1016/j.shpsa.2023.11.007 . ISSN   0039-3681 . ПМИД   38128443 . S2CID   266440296 .
  8. ^ Фишер, Иоганн; Вендланд, Мартин (октябрь 2023 г.). «К истории ключевых эмпирических межмолекулярных потенциалов» . Жидкостно-фазовые равновесия . 573 : 113876. Бибкод : 2023FlPEq.57313876F . дои : 10.1016/j.fluid.2023.113876 . ISSN   0378-3812 .
  9. ↑ Перейти обратно: Перейти обратно: а б Сан Х., Мамби С.Дж., Мэйпл-младший, Хаглер А.Т. (апрель 1994 г.). «Полноатомное силовое поле ab Initio CFF93 для поликарбонатов». Журнал Американского химического общества . 116 (7): 2978–2987. дои : 10.1021/ja00086a030 . ISSN   0002-7863 .
  10. ^ Хуан Дж., МакКерелл А.Д. (сентябрь 2013 г.). «Силовое поле полноатомного аддитивного белка CHARMM36: проверка на основе сравнения с данными ЯМР» . Журнал вычислительной химии . 34 (25): 2135–45. дои : 10.1002/jcc.23354 . ПМЦ   3800559 . ПМИД   23832629 .
  11. ^ Ван Дж., Вольф Р.М., Колдуэлл Дж.В., Коллман П.А., Дело Д.А. (июль 2004 г.). «Разработка и испытание общего янтарного силового поля» . Журнал вычислительной химии . 25 (9): 1157–74. дои : 10.1002/jcc.20035 . ПМИД   15116359 . S2CID   18734898 .
  12. ↑ Перейти обратно: Перейти обратно: а б Мишра Р.К., Фернандес-Карраско Л., Флатт Р.Дж., Хайнц Х. (июль 2014 г.). «Силовое поле трикальциевого алюмината для характеристики свойств поверхности, начальной гидратации и органически модифицированных поверхностей раздела с атомным разрешением». Транзакции Далтона . 43 (27): 10602–16. дои : 10.1039/c4dt00438h . hdl : 2117/24209 . ПМИД   24828263 .
  13. ^ Эшкрофт, Северо-Запад; Мермин, Северная Дакота; Смолуховский, Р. (1 января 1977 г.). « Физика твердого тела » . Физика сегодня . 30 (1): 61–65. Бибкод : 1977ФТ....30Р..61А . дои : 10.1063/1.3037370 . ISSN   0031-9228 .
  14. ^ Терсофф, Дж. (15 апреля 1988 г.). «Новый эмпирический подход к исследованию структуры и энергии ковалентных систем» . Физический обзор B . 37 (12): 6991–7000. Бибкод : 1988PhRvB..37.6991T . дои : 10.1103/physrevb.37.6991 . ISSN   0163-1829 . ПМИД   9943969 .
  15. ^ Доу, Мюррей С.; Баскес, Мичиган (15 июня 1984 г.). «Метод встроенного атома: вывод и применение к примесям, поверхностям и другим дефектам металлов» . Физический обзор B . 29 (12): 6443–6453. Бибкод : 1984PhRvB..29.6443D . дои : 10.1103/physrevb.29.6443 . ISSN   0163-1829 .
  16. ^ Доу, Мюррей С.; Фойлс, Стивен М.; Баскес, Майкл И. (март 1993 г.). «Метод встроенного атома: обзор теории и приложений» . Отчеты по материаловедению . 9 (7–8): 251–310. дои : 10.1016/0920-2307(93)90001-у . ISSN   0920-2307 .
  17. ^ Лемкул Дж.А., Хуанг Дж., Ру Б., МакКерелл А.Д. (май 2016 г.). «Эмпирическое поляризуемое силовое поле на основе классической модели осциллятора Друде: история развития и недавние применения» . Химические обзоры . 116 (9): 4983–5013. doi : 10.1021/acs.chemrev.5b00505 . ПМЦ   4865892 . ПМИД   26815602 .
  18. ^ Лоренц Х.А. (1905). «Движение электронов в металлических телах, I.». Учеб. К. Нед. Акад. Влажный . 7 : 451. Бибкод : 1904KNAB....7..438L .
  19. ^ Друде П. (1900). «К электронной теории металлов. Часть I» . Анналы физики . 306 (3): 566–613. дои : 10.1002/andp.19003060312 .
  20. ^ Йоргенсен В.Л., Максвелл Д.С., Тирадо-Ривз Дж. (январь 1996 г.). «Разработка и тестирование общеатомного силового поля OPLS на конформационную энергетику и свойства органических жидкостей». Журнал Американского химического общества . 118 (45): 11225–11236. дои : 10.1021/ja9621760 . ISSN   0002-7863 .
  21. ↑ Перейти обратно: Перейти обратно: а б с Даубер-Осгуторп П., Робертс В.А., Осгуторп Дж., Вольф Дж., Дженест М., Хаглер А.Т. (1988). «Структура и энергетика связывания лиганда с белками: дигидрофолатредуктаза-триметоприм Escherichia coli, система лекарство-рецептор». Белки . 4 (1): 31–47. дои : 10.1002/прот.340040106 . ПМИД   3054871 . S2CID   2845395 .
  22. ^ Адури Р., Пщук Б.Т., Саро П., Танига Х., Шлегель Х.Б., СантаЛюсия Дж. (июль 2007 г.). «Параметры силового поля ЯНТАРЯ для встречающихся в природе модифицированных нуклеозидов в РНК». Журнал химической теории и вычислений . 3 (4): 1464–75. дои : 10.1021/ct600329w . ПМИД   26633217 .
  23. ^ Киршнер К.Н., Линс Р.Д., Маасс А., Соарес Т.А. (ноябрь 2012 г.). «Силовое поле на основе гликама для моделирования липополисахаридных мембран: параметризация и проверка». Журнал химической теории и вычислений . 8 (11): 4719–31. дои : 10.1021/ct300534j . ПМИД   26605626 .
  24. ^ Гросс К.К., Сейболд П.Г., Хадад К.М. (2002). «Сравнение различных схем атомного заряда для прогнозирования изменений pKa в замещенных анилинах и фенолах». Международный журнал квантовой химии . 90 (1): 445–458. дои : 10.1002/qua.10108 . ISSN   0020-7608 .
  25. ^ Ван Б., Ли С.Л., Трулар Д.Г. (декабрь 2014 г.). «Моделирование парциальных атомных зарядов в неорганометаллических молекулах и твердых телах и перераспределение заряда в литий-ионных катодах» . Журнал химической теории и вычислений . 10 (12): 5640–50. дои : 10.1021/ct500790p . ПМИД   26583247 .
  26. ↑ Перейти обратно: Перейти обратно: а б Хайнц Х., Сутер UW (ноябрь 2004 г.). «Атомные заряды для классического моделирования полярных систем». Журнал физической химии Б. 108 (47): 18341–18352. Бибкод : 2004APS..MAR.Y8006H . дои : 10.1021/jp048142t . ISSN   1520-6106 .
  27. ^ Дхармавардхана CC, Канхайя К., Лин Т.Дж., Гарли А., Кнехт М.Р., Чжоу Дж., Мяо Дж., Хайнц Х. (19 июня 2017 г.). «Надежное вычислительное проектирование биологически-неорганических материалов в большом нанометровом масштабе с использованием Interface-FF». Молекулярное моделирование . 43 (13–16): 1394–1405. дои : 10.1080/08927022.2017.1332414 . ISSN   0892-7022 . S2CID   36710284 .
  28. ^ Ван Л.П., Мартинес Т.Дж., Панде В.С. (июнь 2014 г.). «Создание силовых полей: автоматический, систематический и воспроизводимый подход» . Журнал физической химии . 5 (11): 1885–91. дои : 10.1021/jz500737m . ПМЦ   9649520 . ПМИД   26273869 .
  29. ↑ Перейти обратно: Перейти обратно: а б МакДонах Дж.Л., Шкурти А., Брей DJ, Андерсон Р.Л., Пайзер-Кнапп Э.О. (октябрь 2019 г.). «Использование машинного обучения для эффективной параметризации крупнозернистых молекулярных силовых полей». Журнал химической информации и моделирования . 59 (10): 4278–4288. doi : 10.1021/acs.jcim.9b00646 . ПМИД   31549507 . S2CID   202745539 .
  30. ^ Тадмор, Е.Б.; Эллиотт, RS; Сетна, JP; Миллер, Р.Э.; Беккер, Калифорния (июль 2011 г.). «Потенциал атомистического моделирования и база знаний межатомных моделей» . ДЖОМ . 63 (7): 17. Бибкод : 2011JOM....63г..17Т . дои : 10.1007/s11837-011-0102-6 . ISSN   1047-4838 .
  31. ^ Эггиманн, Бекки Л.; Суннарборг, Амара Дж.; Стерн, Хадсон Д.; Блисс, Эндрю П.; Зипманн, Дж. Илья (2 января 2014 г.). «Онлайн-база данных параметров и свойств силового поля TraPPE» . Молекулярное моделирование . 40 (1–3): 101–105. дои : 10.1080/08927022.2013.842994 . ISSN   0892-7022 . S2CID   95716947 .
  32. ^ Шмитт, Себастьян; Канагалингам, Гаджанан; Флекенштейн, Флориан; Фрёшер, Дэниел; Хассе, Ганс; Стефан, Саймон (27 ноября 2023 г.). «Расширение базы данных MolMod для переносимых силовых полей» . Журнал химической информации и моделирования . 63 (22): 7148–7158. doi : 10.1021/acs.jcim.3c01484 . ISSN   1549-9596 . ПМИД   37947503 . S2CID   265103133 .
  33. ^ Хайнц Х., Рамесани-Дахель Х. (январь 2016 г.). «Моделирование неорганических и биоорганических интерфейсов для открытия новых материалов: идеи, сравнения с экспериментами, проблемы и возможности». Обзоры химического общества . 45 (2): 412–48. дои : 10.1039/c5cs00890e . ПМИД   26750724 .
  34. ^ Эмами Ф.С., Падду В., Берри Р.Дж., Варшни В., Патвардхан С.В., Перри CC, Хайнц Х (22 апреля 2014 г.). «Силовое поле и база данных моделей поверхности кремнезема для моделирования межфазных свойств в атомном разрешении» (PDF) . Химия материалов . 26 (8): 2647–2658. дои : 10.1021/см500365c . ISSN   0897-4756 .
  35. ^ Руис В.Г., Лю В., Ткаченко А (15 января 2016 г.). «Теория функционала плотности с экранированными взаимодействиями Ван-дер-Ваальса в применении к атомным и молекулярным адсорбатам на плотноупакованных и неплотноупакованных поверхностях». Физический обзор B . 93 (3): 035118. Бибкод : 2016PhRvB..93c5118R . дои : 10.1103/physrevb.93.035118 . hdl : 11858/00-001M-0000-0029-3035-8 . ISSN   2469-9950 .
  36. ^ Руис В.Г., Лю В., Зойер Э., Шеффлер М., Ткаченко А. (апрель 2012 г.). «Теория функционала плотности с экранированными ван-дер-ваальсовыми взаимодействиями для моделирования гибридных неорганических-органических систем» . Письма о физических отзывах . 108 (14): 146103. Бибкод : 2012PhRvL.108n6103R . дои : 10.1103/physrevlett.108.146103 . hdl : 11858/00-001M-0000-000F-C6EA-3 . ПМИД   22540809 .
  37. ^ Крамер С., Спинн А., Лидл К.Р. (октябрь 2014 г.). «Анизотропия заряда: где атомные мультиполи имеют наибольшее значение». Журнал химической теории и вычислений . 10 (10): 4488–96. дои : 10.1021/ct5005565 . ПМИД   26588145 .
  38. ^ Махони М.В., Йоргенсен В.Л. (22 мая 2000 г.). «Пятиузловая модель жидкой воды и воспроизведение аномалии плотности жесткими неполяризуемыми потенциальными функциями». Журнал химической физики . 112 (20): 8910–8922. Бибкод : 2000JChPh.112.8910M . дои : 10.1063/1.481505 . ISSN   0021-9606 .
  39. ↑ Перейти обратно: Перейти обратно: а б Сюй Р., Чен С.С., Ву Л., Скотт М.К., Тейс В., Офус С. и др. (ноябрь 2015 г.). «Трехмерные координаты отдельных атомов в материалах, выявленные с помощью электронной томографии». Природные материалы . 14 (11): 1099–103. arXiv : 1505.05938 . Бибкод : 2015NatMa..14.1099X . дои : 10.1038/nmat4426 . ПМИД   26390325 . S2CID   5455024 .
  40. ↑ Перейти обратно: Перейти обратно: а б Праманик С., Гиссинджер-младший, Кумар С., Хайнц Х. (декабрь 2017 г.). «Дисперсия углеродных нанотрубок в растворителях и растворах полимеров: механизмы, сборка и предпочтения». АСУ Нано . 11 (12): 12805–12816. дои : 10.1021/acsnano.7b07684 . ПМИД   29179536 .
  41. ↑ Перейти обратно: Перейти обратно: а б с Ломизе А.Л., Рейбарх М.Ю., Погожева И.Д. (август 2002 г.). «Межатомные потенциалы и параметры сольватации на основе данных белковой инженерии для захороненных остатков» . Белковая наука . 11 (8): 1984–2000. дои : 10.1110/ps.0307002 . ПМК   2373680 . ПМИД   12142453 .
  42. ↑ Перейти обратно: Перейти обратно: а б Варшел А., Шарма П.К., Като М., Парсон В.В. (ноябрь 2006 г.). «Моделирование электростатических эффектов в белках». Biochimica et Biophysical Acta (BBA) - Белки и протеомика . 1764 (11): 1647–76. дои : 10.1016/j.bbapap.2006.08.007 . ПМИД   17049320 .
  43. ^ Шютц CN, Варшел А (сентябрь 2001 г.). «Каковы диэлектрические «константы» белков и как проверить электростатические модели?». Белки . 44 (4): 400–17. дои : 10.1002/прот.1106 . ПМИД   11484218 . S2CID   9912122 .
  44. ↑ Перейти обратно: Перейти обратно: а б с д и Исраелачвили Ю.Н. (2011). «Межмолекулярные и поверхностные силы». Эльзевир. стр. iii. дои : 10.1016/b978-0-12-391927-4.10024-6 . ISBN  978-0-12-391927-4 . {{cite book}}: Отсутствует или пусто |title= ( помощь )
  45. ^ Лекбанд Д., Исраэлачвили Дж. (май 2001 г.). «Межмолекулярные силы в биологии». Ежеквартальные обзоры биофизики . 34 (2): 105–267. дои : 10.1017/S0033583501003687 . ПМИД   11771120 . S2CID   8401242 .
  46. ^ Праманик С., Джамиль Т., Гиссинджер-младший, Гитте Д., Ариас-Монже П.Дж., Кумар С., Хайнц Х. (03.10.2019). «Взаимодействие полиакрилонитрила с углеродными нанотрубками в растворе: конформация и связывание в зависимости от растворителя, температуры и концентрации». Передовые функциональные материалы . 29 (50): 1905247. doi : 10.1002/adfm.201905247 . ISSN   1616-301X . S2CID   208700020 .
  47. ^ Кёль П., Левитт М. (февраль 1999 г.). «Светлое будущее предсказания структуры белка». Структурная биология природы . 6 (2): 108–11. дои : 10.1038/5794 . ПМИД   10048917 . S2CID   3162636 .
  48. ^ Брунгер А.Т., Адамс П.Д. (июнь 2002 г.). «Молекулярная динамика применительно к уточнению рентгеновской структуры». Отчеты о химических исследованиях . 35 (6): 404–12. дои : 10.1021/ar010034r . ПМИД   12069625 .
  49. ^ Гюнтерт П. (май 1998 г.). «Расчет структуры биологических макромолекул по данным ЯМР». Ежеквартальные обзоры биофизики . 31 (2): 145–237. дои : 10.1017/S0033583598003436 . ПМИД   9794034 . S2CID   43575627 .
  50. ^ Остермейр К., Захариас М. (январь 2013 г.). «163 Улучшенный отбор проб пептидов и белков с помощью нового метода смещения реплик» . Журнал биомолекулярной структуры и динамики . 31 (sup1): 106. doi : 10.1080/07391102.2013.786405 . ISSN   0739-1102 . S2CID   98441607 .
  51. ^ Трамонтано А, Мореа В (2003). «Оценка предсказаний на основе гомологии в CASP5» . Белки . 53 (Приложение 6): 352–68. дои : 10.1002/прот.10543 . ПМИД   14579324 . S2CID   33186021 .
  52. ^ Гольке Х., Клебе Г. (август 2002 г.). «Подходы к описанию и прогнозированию сродства связывания низкомолекулярных лигандов с макромолекулярными рецепторами». Ангеванде Хеми . 41 (15): 2644–76. doi : 10.1002/1521-3773(20020802)41:15<2644::AID-ANIE2644>3.0.CO;2-O . ПМИД   12203463 .
  53. ^ Эджкомб С.П., Мерфи К.П. (февраль 2000 г.). «Структурная энергетика сворачивания и связывания белков». Современное мнение в области биотехнологии . 11 (1): 62–6. дои : 10.1016/s0958-1669(99)00055-5 . ПМИД   10679345 .
  54. ^ Лазаридис Т., Карплюс М. (апрель 2000 г.). «Эффективные энергетические функции для предсказания структуры белка». Современное мнение в области структурной биологии . 10 (2): 139–45. дои : 10.1016/s0959-440x(00)00063-4 . ПМИД   10753811 .
  55. ^ Джавидпур Л. (2012). «Компьютерное моделирование сворачивания белка». Вычисления в науке и технике . 14 (2): 97–103. Бибкод : 2012CSE....14b..97J . дои : 10.1109/MCSE.2012.21 . S2CID   17613729 .
  56. ^ Кригер Э., Джу К., Ли Дж., Ли Дж., Раман С., Томпсон Дж. и др. (2009). «Повышение физического реализма, стереохимии и точности боковой цепи при моделировании гомологии: четыре подхода, которые хорошо зарекомендовали себя в CASP8» . Белки . 77 (Приложение 9): 114–22. дои : 10.1002/прот.22570 . ПМК   2922016 . ПМИД   19768677 .
  57. ^ Гордон Д.Б., Маршалл С.А., Мэйо С.Л. (август 1999 г.). «Энергетические функции для дизайна белков». Современное мнение в области структурной биологии . 9 (4): 509–13. дои : 10.1016/S0959-440X(99)80072-4 . ПМИД   10449371 .
  58. ^ Мендес Дж., Геруа Р., Серрано Л. (август 2002 г.). «Оценка энергии в дизайне белков». Современное мнение в области структурной биологии . 12 (4): 441–6. дои : 10.1016/s0959-440x(02)00345-7 . ПМИД   12163065 .
  59. ^ Рол К.А., Штраус К.Э., Мисура К.М., Бейкер Д. (2004). «Прогнозирование структуры белка с помощью Rosetta». Численные компьютерные методы, Часть D. Методы энзимологии. Том. 383. стр. 66–93. дои : 10.1016/S0076-6879(04)83004-0 . ISBN  9780121827885 . ПМИД   15063647 .
  60. ^ Ломизе А.Л., Погожева И.Д., Ломизе М.А., Мосберг Х.И. (июнь 2006 г.). «Позиционирование белков в мембранах: вычислительный подход» . Белковая наука . 15 (6): 1318–33. дои : 10.1110/ps.062126106 . ПМК   2242528 . ПМИД   16731967 .
  61. ^ Мерфи К.П., Гилл С.Дж. (декабрь 1991 г.). «Твердые модельные соединения и термодинамика разворачивания белка». Журнал молекулярной биологии . 222 (3): 699–709. дои : 10.1016/0022-2836(91)90506-2 . ПМИД   1660931 .
  62. ^ Шахнович Е.И., Финкельштейн А.В. (октябрь 1989 г.). «Теория кооперативных переходов в белковых молекулах. I. Почему денатурация глобулярного белка является фазовым переходом первого рода». Биополимеры . 28 (10): 1667–80. дои : 10.1002/bip.360281003 . ПМИД   2597723 . S2CID   26981215 .
  63. ^ Грациано Дж., Катанцано Ф., Дель Веккьо П., Джанкола С., Бароне Дж. (1996). «Термодинамическая стабильность глобулярных белков: надежная модель исследований малых молекул». Газетта Хим. Итальяна . 126 : 559–567.
  64. ^ Майерс Дж. К., Пейс CN (октябрь 1996 г.). «Водородная связь стабилизирует глобулярные белки» . Биофизический журнал . 71 (4): 2033–9. Бибкод : 1996BpJ....71.2033M . дои : 10.1016/S0006-3495(96)79401-8 . ПМЦ   1233669 . ПМИД   8889177 .
  65. ^ Шольц Дж.М., Маркизи С., Болдуин Р.Л., Йорк Э.Дж., Стюарт Дж.М., Санторо М., Болен Д.В. (апрель 1991 г.). «Колориметрическое определение изменения энтальпии перехода альфа-спирали в спираль аланинового пептида в воде» . Труды Национальной академии наук Соединенных Штатов Америки . 88 (7): 2854–8. Бибкод : 1991PNAS...88.2854S . дои : 10.1073/pnas.88.7.2854 . ПМК   51338 . ПМИД   2011594 .
  66. ^ Гавецотти А., Филиппини Дж. (май 1994 г.). «Геометрия межмолекулярной водородной связи XH. cntdot.. cntdot.. cntdot. Y (X, Y = N, O) и калибровка эмпирических потенциалов водородной связи». Журнал физической химии . 98 (18): 4831–7. дои : 10.1021/j100069a010 .
  67. ^ Мёлльхофф М., Штернберг У. (май 2001 г.). «Молекулярная механика с флуктуирующими атомными зарядами – новое силовое поле с полуэмпирическим расчетом заряда». Ежегодник молекулярного моделирования . 7 (4): 90–102. дои : 10.1007/s008940100008 . S2CID   91705326 .
  68. ^ «ЭКЭПП» . biohpc.cornell.edu .
  69. ^ Момани Ф.А., Макгуайр Р.Ф., Берджесс А.В., Шерага Х.А. (октябрь 1975 г.). «Энергетические параметры в полипептидах. VII. Геометрические параметры, частичные атомные заряды, несвязанные взаимодействия, взаимодействия водородных связей и собственные торсионные потенциалы для встречающихся в природе аминокислот». Журнал физической химии . 79 (22): 2361–81. дои : 10.1021/j100589a006 .
  70. ^ Арнаутова Ю.А., Ягельская А., Шерага Х.А. (март 2006 г.). «Новое силовое поле (ECEPP-05) для пептидов, белков и органических молекул». Журнал физической химии Б. 110 (10): 5025–44. дои : 10.1021/jp054994x . ПМИД   16526746 .
  71. ^ Шауманн Т., Браун В., Вютрих К. (март 1990 г.). «Программа FANTOM для энергетического уточнения полипептидов и белков с использованием минимизатора Ньютона – Рафсона в пространстве торсионных углов». Биополимеры . 29 (4–5): 679–94. дои : 10.1002/bip.360290403 . S2CID   94519023 .
  72. ^ «ГРОМОС» . www.igc.ethz.ch. ​
  73. ↑ Перейти обратно: Перейти обратно: а б Хайнц Х., Лин Т.Дж., Мишра Р.К., Эмами Ф.С. (февраль 2013 г.). «Термодинамически согласованные силовые поля для сборки неорганических, органических и биологических наноструктур: силовое поле INTERFACE». Ленгмюр . 29 (6): 1754–65. дои : 10.1021/la3038846 . ПМИД   23276161 .
  74. ^ «Интерфейсное силовое поле (IFF)» . Лаборатория Хайнца . 2 февраля 2016 г.
  75. ↑ Перейти обратно: Перейти обратно: а б Мишра Р.К., Мохамед А.К., Гейссбюлер Д., Мансано Х., Джамиль Т., Шахсавари Р., Калиничев А.Г., Гальмарини С., Тао Л., Хайнц Х., Пелленк Р. (декабрь 2017 г.). «База данных силовых полей для вяжущих материалов, включая проверки, приложения и возможности» (PDF) . Исследования цемента и бетона . 102 : 68–89. doi : 10.1016/j.cemconres.2017.09.003 .
  76. ↑ Перейти обратно: Перейти обратно: а б Геада И.Л., Рамесани-Дахель Х., Джамиль Т., Сульпизи М., Хайнц Х. (февраль 2018 г.). «Изучение индуцированных зарядов на металлических поверхностях и биоинтерфейсах с использованием поляризуемого потенциала Леннарда-Джонса» . Природные коммуникации . 9 (1): 716. Бибкод : 2018NatCo...9..716G . дои : 10.1038/s41467-018-03137-8 . ПМК   5818522 . ПМИД   29459638 .
  77. ^ Аллингер Н.Л. (декабрь 1977 г.). «Конформационный анализ. 130. MM2. Силовое поле углеводородов с использованием крутильных членов V1 и V2». Журнал Американского химического общества . 99 (25): 8127–34. дои : 10.1021/ja00467a001 .
  78. ^ «Домашняя страница MM2 и MM3» . Архивировано из оригинала 23 января 2009 г.
  79. ^ Аллинджер Н.Л., Ю Ю.Х., Лии Дж.Х. (ноябрь 1989 г.). «Молекулярная механика. Силовое поле ММ3 для углеводородов. 1». Журнал Американского химического общества . 111 (23): 8551–66. дои : 10.1021/ja00205a001 .
  80. ^ Лий Дж. Х., Аллингер, Н.Л. (ноябрь 1989 г.). «Молекулярная механика. Силовое поле ММ3 для углеводородов. 2. Частоты колебаний и термодинамика». Журнал Американского химического общества . 111 (23): 8566–75. дои : 10.1021/ja00205a002 .
  81. ^ Лий Дж. Х., Аллингер, Н.Л. (ноябрь 1989 г.). «Молекулярная механика. Силовое поле ММ3 для углеводородов. 3. Потенциалы Ван-дер-Ваальса и кристаллические данные для алифатических и ароматических углеводородов». Журнал Американского химического общества . 111 (23): 8576–82. дои : 10.1021/ja00205a003 .
  82. ^ Варшел А (1973). «Метод квантово-механического согласованного силового поля (QCFF/PI): расчеты энергий, конформаций и вибронных взаимодействий основного и возбужденного состояний сопряженных молекул». Израильский химический журнал . 11 (5): 709–17. дои : 10.1002/ijch.197300067 .
  83. ^ Варшел А., Левитт М. (1974). QCFF/PI: Программа для последовательной оценки силового поля равновесной геометрии и частот колебаний молекул (Отчет). Университет Индианы: обмен программами по квантовой химии. п. ПКПЕ 247.
  84. ^ Раппе А.К., Кейзевит С.Дж., Колвелл К.С., Годдард III WA, Скиф В.М. (декабрь 1992 г.). «UFF, полное силовое поле таблицы Менделеева для моделирования молекулярной механики и молекулярной динамики». Журнал Американского химического общества . 114 (25): 10024–10035. дои : 10.1021/ja00051a040 . ISSN   0002-7863 .
  85. ^ Хайнц Х., Кернер Х., Андерсон К.Л., Вайя Р.А., Фармер Б.Л. (ноябрь 2005 г.). «Силовое поле для силикатов типа слюды и динамика цепей октадециламмония, привитых к монтмориллониту». Химия материалов . 17 (23): 5658–5669. дои : 10.1021/cm0509328 . ISSN   0897-4756 .
  86. ^ Дик Б.Г., Оверхаузер А.В. (1 октября 1958 г.). «Теория диэлектрических проницаемостей щелочно-галоидных кристаллов». Физический обзор . 112 (1): 90–103. Бибкод : 1958PhRv..112...90D . дои : 10.1103/physrev.112.90 . ISSN   0031-899X .
  87. ^ Митчелл П.Дж., Финчем Д. (22 февраля 1993 г.). «Моделирование модели оболочки с помощью адиабатической динамики». Физический журнал: конденсированное вещество . 5 (8): 1031–1038. Бибкод : 1993JPCM....5.1031M . дои : 10.1088/0953-8984/5/8/006 . ISSN   0953-8984 . S2CID   250752417 .
  88. ^ Ю Х, ван Гюнстерен В.Ф. (ноябрь 2005 г.). «Учет поляризации в молекулярном моделировании». Компьютерная физика. Коммуникации . 172 (2): 69–85. Бибкод : 2005CoPhC.172...69Y . дои : 10.1016/j.cpc.2005.01.022 . ISSN   0010-4655 .
  89. ↑ Перейти обратно: Перейти обратно: а б Патель С., Брукс К.Л. (январь 2004 г.). «Поле флуктуирующих сил заряда CHARMM для белков: параметризация и применение к моделированию объемных органических жидкостей». Журнал вычислительной химии . 25 (1): 1–15. дои : 10.1002/jcc.10355 . ПМИД   14634989 . S2CID   39320318 .
  90. ^ Ян Л., Тан Ч., Се М.Дж., Ван Дж., Дуань Ю., Чеплак П., Колдуэлл Дж., Коллман П.А., Луо Р. (июль 2006 г.). «Янтарное силовое поле объединенного атома нового поколения». Журнал физической химии Б. 110 (26): 13166–76. дои : 10.1021/jp060163v . ПМИД   16805629 .
  91. ^ «Пакет Tinker для молекулярного моделирования» . Dasher.wustl.edu .
  92. ^ Лю С., Пикемаль Дж.П., Рен П. (январь 2020 г.). «Внедрение геометрически-зависимого потока заряда в поляризуемый потенциал AMOEBA+» . Журнал физической химии . 11 (2): 419–426. doi : 10.1021/acs.jpclett.9b03489 . ПМЦ   7384396 . ПМИД   31865706 .
  93. ^ Лю С., Пикемаль Дж.П., Рен П. (июль 2019 г.). «Классический потенциал AMOEBA + для моделирования молекулярных взаимодействий» . Журнал химической теории и вычислений . 15 (7): 4122–4139. дои : 10.1021/acs.jctc.9b00261 . ПМК   6615954 . ПМИД   31136175 .
  94. ^ Патель С., Маккерелл А.Д., Брукс К.Л. (сентябрь 2004 г.). «Поле флуктуирующих сил заряда CHARMM для белков: II свойства белка/растворителя на основе молекулярно-динамического моделирования с использованием неаддитивной электростатической модели» . Журнал вычислительной химии . 25 (12): 1504–14. дои : 10.1002/jcc.20077 . ПМИД   15224394 . S2CID   16741310 .
  95. ^ Анисимов В.М., Ламуре Г., Воробьев И.В., Хуанг Н., Ру Б., МакКерелл А.Д. (январь 2005 г.). «Определение электростатических параметров поляризуемого силового поля на основе классического генератора Друде». Журнал химической теории и вычислений . 1 (1): 153–68. дои : 10.1021/ct049930p . ПМИД   26641126 .
  96. ^ Ю Х, Уитфилд Т.В., Хардер Э., Ламуре Г., Воробьев И., Анисимов В.М., Маккерелл А.Д., Ру Б (2010). «Моделирование одновалентных и двухвалентных ионов в водном растворе с использованием поляризуемого силового поля Друде» . Журнал химической теории и вычислений . 6 (3): 774–786. дои : 10.1021/ct900576a . ПМЦ   2838399 . ПМИД   20300554 .
  97. ^ Варшел А., Левитт М. (май 1976 г.). «Теоретические исследования ферментативных реакций: диэлектрическая, электростатическая и стерическая стабилизация иона карбония в реакции лизоцима». Журнал молекулярной биологии . 103 (2): 227–49. дои : 10.1016/0022-2836(76)90311-9 . ПМИД   985660 .
  98. ^ Штернберг У., Кох Ф.Т., Мёлльхофф М. (май 1994 г.). «Новый подход к полуэмпирическому расчету атомных зарядов полипептидов и крупных молекулярных систем». Журнал вычислительной химии . 15 (5): 524–31. дои : 10.1002/jcc.540150505 . S2CID   5227353 .
  99. ^ Сварт М., ван Дуйнен П.Т. (май 2006 г.). «DRF90: поляризуемое силовое поле». Молекулярное моделирование . 32 (6): 471–84. дои : 10.1080/08927020600631270 . S2CID   96616243 .
  100. ^ Энгквист О., Астранд П.О., Карлстрем Г. (ноябрь 2000 г.). «Точные межмолекулярные потенциалы, полученные с помощью молекулярных волновых функций: преодоление разрыва между квантовой химией и молекулярным моделированием». Химические обзоры . 100 (11): 4087–108. дои : 10.1021/cr9900477 . ПМИД   11749341 .
  101. ^ Гао Дж., Хабиболлазаде Д., Шао Л. (ноябрь 1995 г.). «Поляризуемая межмолекулярная потенциальная функция для моделирования жидких спиртов». Журнал физической химии . 99 (44): 16460–7. дои : 10.1021/j100044a039 .
  102. ^ Се В., Пу Дж., Маккерелл А.Д., Гао Дж. (2007). «Разработка поляризуемой межмолекулярной потенциальной функции (ММПФ) для жидких амидов и алканов» . Журнал химической теории и вычислений . 3 (6): 1878–1889. дои : 10.1021/ct700146x . ПМЦ   2572772 . ПМИД   18958290 .
  103. ^ Мэйпл-младший, Цао И., Дамм В., Халгрен Т.А., Камински Г.А., Чжан Л.Ю., Фриснер Р.А. (июль 2005 г.). «Поляризуемое силовое поле и методология сольватации континуума для моделирования взаимодействий белок-лиганд». Журнал химической теории и вычислений . 1 (4): 694–715. дои : 10.1021/ct049855i . ПМИД   26641692 .
  104. ^ Челли Р., Прокаччи П. (ноябрь 2002 г.). «Переносное поляризуемое электростатическое силовое поле для молекулярной механики, основанное на принципе выравнивания химических потенциалов». Журнал химической физики . 117 (20): 9175–89. Бибкод : 2002JChPh.117.9175C . дои : 10.1063/1.1515773 .
  105. ^ Чиосе Ч.Р., Маклафлин К., Белоф Дж.Л., Space B (декабрь 2013 г.). «Поляризуемый и переносимый потенциал PHAST N2 для использования при моделировании материалов». Журнал химической теории и вычислений . 9 (12): 5550–7. дои : 10.1021/ct400526a . ПМИД   26592288 .
  106. ^ «Энтони Стоун: Компьютерные программы» . www-stone.ch.cam.ac.uk .
  107. ^ Греш Н., Сиснерос Г.А., Дарден Т.А., Пикемаль Дж.П. (ноябрь 2007 г.). «Анизотропные, поляризующиеся молекулярно-механические исследования меж- и внутримолекулярных взаимодействий и лиганд-макромолекулярных комплексов. Стратегия снизу вверх» . Журнал химической теории и вычислений . 3 (6): 1960–1986. дои : 10.1021/ct700134r . ПМК   2367138 . ПМИД   18978934 .
  108. ^ Пикемаль Дж. П., Сиснерос Г. А., Рейнхардт П., Греш Н., Дарден Т. А. (март 2006 г.). «К силовому полю, основанному на подгонке плотности» . Журнал химической физики . 124 (10): 104101. Бибкод : 2006JChPh.124j4101P . дои : 10.1063/1.2173256 . ПМК   2080832 . ПМИД   16542062 .
  109. ^ Сиснерос Г.А., Пикемаль Дж.П., Дарден Т.А. (ноябрь 2006 г.). «Обобщение гауссовской электростатической модели: расширение до произвольного углового момента, распределенные мультиполи и ускорение с помощью методов обратного пространства» . Журнал химической физики . 125 (18): 184101. Бибкод : 2006JChPh.125r4101C . дои : 10.1063/1.2363374 . ПМК   2080839 . ПМИД   17115732 .
  110. ^ Бородин О. (август 2009 г.). «Развитие поляризуемого силового поля и моделирование молекулярной динамики ионных жидкостей». Журнал физической химии Б. 113 (33): 11463–78. дои : 10.1021/jp905220k . ПМИД   19637900 .
  111. ^ Спичер С., Гримме С. (сентябрь 2020 г.). «Надежное атомистическое моделирование материалов, металлоорганических и биохимических систем» . Angewandte Chemie, международное издание . 59 (36): 15665–15673. дои : 10.1002/anie.202004239 . ПМЦ   7267649 . ПМИД   32343883 .
  112. ^ Старовойтов О.Н. (сентябрь 2021 г.). «Разработка поляризуемого силового поля для молекулярно-динамического моделирования электролитов литий-ионных аккумуляторов: растворителей на основе сульфонатов и солей лития». Журнал физической химии Б. 125 (40): 11242–11255. doi : 10.1021/acs.jpcb.1c05744 . ПМИД   34586817 . S2CID   238230196 .
  113. ^ ван Дуин А.С., Дасгупта С., Лорант Ф., Годдард В.А. (2001). «ReaxFF: Поле реактивной силы для углеводородов» (PDF) . Журнал физической химии А. 105 (41): 9396–9409. Бибкод : 2001JPCA..105.9396V . CiteSeerX   10.1.1.507.6992 . дои : 10.1021/jp004368u . Архивировано из оригинала (PDF) 21 марта 2018 г. Проверено 29 августа 2015 г.
  114. ^ Хугербрюгге П.Дж., Кельман Дж.М. (1992). «Моделирование микроскопических гидродинамических явлений с помощью диссипативной динамики частиц». Письма по еврофизике (EPL) . 19 (3): 155–160. Бибкод : 1992EL.....19..155H . дои : 10.1209/0295-5075/19/3/001 . ISSN   0295-5075 . S2CID   250796817 .
  115. ^ Кельман Дж. М., Хугербрюгге П. Дж. (1993). «Динамическое моделирование суспензий твердых сфер при постоянном сдвиге». Письма по еврофизике (EPL) . 21 (3): 363–368. Бибкод : 1993EL.....21..363K . дои : 10.1209/0295-5075/21/3/018 . ISSN   0295-5075 . S2CID   250913111 .
  116. ^ Эспаньол П., Уоррен П. (1995). «Статистическая механика диссипативной динамики частиц». Письма по еврофизике (EPL) . 30 (4): 191–196. Бибкод : 1995EL.....30..191E . дои : 10.1209/0295-5075/30/4/001 . ISSN   0295-5075 . S2CID   14385201 .
  117. ^ Динамика диссипативных частиц: устранение недостатков и установление новых границ. Архивировано 15 июля 2010 г. в Wayback Machine , семинар CECAM, 16–18 июля 2008 г., Лозанна, Швейцария.
  118. ^ «САФТ» .
  119. ^ Коркут А., Хендриксон В.А. (сентябрь 2009 г.). «Силовое поле для виртуальной атомной молекулярной механики белков» . Труды Национальной академии наук Соединенных Штатов Америки . 106 (37): 15667–72. Бибкод : 2009PNAS..10615667K . дои : 10.1073/pnas.0907674106 . ПМЦ   2734882 . ПМИД   19717427 .
  120. ^ Бататия И., Ковач Д.П., Симм Г., Ортнер С., Чаньи Г. (2022). «MACE: эквивариантные нейронные сети высшего порядка, передающие сообщения для быстрых и точных силовых полей» . Достижения в области нейронных систем обработки информации . 35 : 11423–11436. arXiv : 2206.07697 .
  121. ^ Смит Дж.С., Исаев О., Ройтберг А.Е. (апрель 2017 г.). «ANI-1: расширяемый потенциал нейронной сети с точностью DFT и затратами на вычисления силового поля» . Химическая наука . 8 (4): 3192–3203. дои : 10.1039/C6SC05720A . ПМЦ   5414547 . ПМИД   28507695 .
  122. ^ Хьюз З.Э., Такер Дж.К., Уилсон А.Л., Попелье П.Л. (январь 2019 г.). «Описание поверхностей потенциальной энергии молекул с использованием моделей машинного обучения FFLUX». Журнал химической теории и вычислений . 15 (1): 116–126. дои : 10.1021/acs.jctc.8b00806 . hdl : 10454/16776 . ПМИД   30507180 . S2CID   54524604 .
  123. ^ Флетчер Т.Л., Попелье П.Л. (июнь 2016 г.). «Прогнозирование многополярной электростатической энергии для всех 20 природных аминокислот с использованием машинного обучения Кригинга» . Журнал химической теории и вычислений . 12 (6): 2742–51. дои : 10.1021/acs.jctc.6b00457 . ПМИД   27224739 .
  124. ^ МакДонах Дж.Л., Сильва А.Ф., Винсент М.А., Попелье П.Л. (январь 2018 г.). «Машинное обучение динамических энергий электронной корреляции из топологических атомов» . Журнал химической теории и вычислений . 14 (1): 216–224. дои : 10.1021/acs.jctc.7b01157 . ПМИД   29211469 .
  125. ^ Рамакришнан Р., Драл П.О., Рупп М., фон Лилиенфельд О.А. (май 2015 г.). «Большие данные соответствуют приближениям квантовой химии: подход Δ-машинного обучения». Журнал химической теории и вычислений . 11 (5): 2087–96. arXiv : 1503.04987 . Бибкод : 2015arXiv150304987R . дои : 10.1021/acs.jctc.5b00099 . ПМИД   26574412 . S2CID   28672393 .
  126. ^ Шютт К.Т., Сауседа Х.Э., Киндерманс П.Дж., Ткаченко А., Мюллер К.Р. (июнь 2018 г.). «SchNet — архитектура глубокого обучения молекул и материалов». Журнал химической физики . 148 (24): 241722. arXiv : 1712.06113 . Бибкод : 2018JChPh.148x1722S . дои : 10.1063/1.5019779 . ПМИД   29960322 . S2CID   4897444 .
  127. ^ ОТ Унке и М. Мьюули (2019). «PhysNet: нейронная сеть для прогнозирования энергии, сил, дипольных моментов и частичных зарядов». Дж. Хим. Тео. Хим . 15 (6): 3678–3693. arXiv : 1902.08408 . дои : 10.1021/acs.jctc.9b00181 . ПМИД   31042390 . S2CID   85543050 .
  128. ^ Молинеро В., Мур Э.Б. (апрель 2009 г.). «Вода смоделирована как промежуточный элемент между углеродом и кремнием». Журнал физической химии Б. 113 (13): 4008–16. arXiv : 0809.2811 . дои : 10.1021/jp805227c . ПМИД   18956896 . S2CID   20782587 .
  129. ^ Хури Г.А., Томпсон Дж.П., Смэдбек Дж., Кислич К.А., Флудас К.А. (декабрь 2013 г.). «Параметры Ab Initio заряда и силового поля AMBER для часто встречающихся посттрансляционных модификаций» . Журнал химической теории и вычислений . 9 (12): 5653–5674. дои : 10.1021/ct400556v . ПМЦ   3904396 . ПМИД   24489522 .
  130. ^ Хури Г.А., Смадбек Дж., Тамамис П., Вандрис А.К., Кислич К.А., Флудас К.А. (декабрь 2014 г.). «Forcefield_NCAA: параметры заряда ab initio, которые помогут в открытии и разработке терапевтических белков и пептидов с неприродными аминокислотами и их применении в качестве ингибиторов комплемента семейства компстатинов» . ACS Синтетическая биология . 3 (12): 855–69. дои : 10.1021/sb400168u . ПМЦ   4277759 . ПМИД   24932669 .
  131. ^ Хури Г.А., Бхатия Н., Флудас К.А. (2014). «Свободная энергия гидратации рассчитана с использованием модели заряда AMBER ff03 для природных и неприродных аминокислот и нескольких моделей воды». Компьютеры и химическая инженерия . 71 : 745–752. doi : 10.1016/j.compchemeng.2014.07.017 .
  132. ^ Дит Р.Дж. (2001). «Модель молекулярной механики поля лигандов и стереоэлектронные эффекты d- и s-электронов». Обзоры координационной химии . 212 (212): 11–34. дои : 10.1016/S0010-8545(00)00354-4 .
  133. ^ Фоскато М., Дит Р.Дж., Дженсен В.Р. (июнь 2015 г.). «Интеграция молекулярной механики поля лигандов в Tinker». Журнал химической информации и моделирования . 55 (6): 1282–90. doi : 10.1021/acs.jcim.5b00098 . HDL : 1956/10456 . ПМИД   25970002 .

Дальнейшее чтение [ править ]

  • Исраэлачвили Ю.Н. (1992). Межмолекулярные и поверхностные силы . Сан-Диего: Академическая пресса. ISBN  978-0-12-375181-2 .
  • Шлик Т. (2002). Молекулярное моделирование и моделирование: междисциплинарное руководство . Междисциплинарная прикладная математика: математическая биология. Нью-Йорк: Springer-Verlag. ISBN  978-0-387-95404-2 .
  • Варшел А. (1991). Компьютерное моделирование химических реакций в ферментах и ​​растворах . Нью-Йорк: Джон Уайли и сыновья. ISBN  978-0-471-53395-5 .
Retrieved from "https://en.wikipedia.org/w/index.php?title=Force_field_(chemistry)&oldid=1226718583"
Arc.Ask3.Ru: конец переведенного документа.
Arc.Ask3.Ru
Номер скриншота №: 77c7a4343ca04919a4915d0caa7af0d8__1717231620
URL1:https://arc.ask3.ru/arc/aa/77/d8/77c7a4343ca04919a4915d0caa7af0d8.html
Заголовок, (Title) документа по адресу, URL1:
Force field (chemistry) - Wikipedia
Данный printscreen веб страницы (снимок веб страницы, скриншот веб страницы), визуально-программная копия документа расположенного по адресу URL1 и сохраненная в файл, имеет: квалифицированную, усовершенствованную (подтверждены: метки времени, валидность сертификата), открепленную ЭЦП (приложена к данному файлу), что может быть использовано для подтверждения содержания и факта существования документа в этот момент времени. Права на данный скриншот принадлежат администрации Ask3.ru, использование в качестве доказательства только с письменного разрешения правообладателя скриншота. Администрация Ask3.ru не несет ответственности за информацию размещенную на данном скриншоте. Права на прочие зарегистрированные элементы любого права, изображенные на снимках принадлежат их владельцам. Качество перевода предоставляется как есть. Любые претензии, иски не могут быть предъявлены. Если вы не согласны с любым пунктом перечисленным выше, вы не можете использовать данный сайт и информация размещенную на нем (сайте/странице), немедленно покиньте данный сайт. В случае нарушения любого пункта перечисленного выше, штраф 55! (Пятьдесят пять факториал, Денежную единицу (имеющую самостоятельную стоимость) можете выбрать самостоятельно, выплаичвается товарами в течение 7 дней с момента нарушения.)