Молекулярная механика

Силовое поле используется для минимизации энергии растяжения связи этой молекулы этана.

Молекулярная механика использует классическую механику для моделирования молекулярных систем. Предполагается, что приближение Борна-Оппенгеймера справедливо, и потенциальная энергия всех систем рассчитывается как функция ядерных координат с использованием силовых полей . Молекулярную механику можно использовать для изучения молекулярных систем различного размера и сложности, от небольших до крупных биологических систем или материальных ансамблей, содержащих от многих тысяч до миллионов атомов.

Методы полноатомистической молекулярной механики обладают следующими свойствами:

• Каждый атом моделируется как одна частица.
• Каждой частице присваивается радиус (обычно радиус Ван-дер-Ваальса ), поляризуемость и постоянный суммарный заряд (обычно получаемый на основе квантовых расчетов и/или экспериментов).
• Связанные взаимодействия рассматриваются как пружины с равновесным расстоянием, равным экспериментальной или расчетной длине связи.

Возможны варианты на эту тему. Например, во многих симуляциях исторически использовалось представление единого атома , в котором каждая концевая метильная группа или промежуточная метиленовая единица считалась одной частицей, а большие белковые системы обычно моделируются с использованием модели шариков , которая присваивает каждой аминокислоте от двух до четырех частиц .

Функциональная форма

Функция потенциальной энергии молекулярной механики с континуальным растворителем.

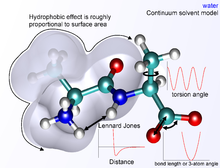
Следующая функциональная абстракция, называемая в химии межатомной потенциальной функцией или силовым полем , рассчитывает потенциальную энергию (E) молекулярной системы в заданной конформации как сумму отдельных энергетических членов.

$\ E=E_{\text{covalent}}+E_{\text{noncovalent}}\,$

где компоненты ковалентного и нековалентного вклада определяются следующим суммированием:

$\ E_{\text{covalent}}=E_{\text{bond}}+E_{\text{angle}}+E_{\text{dihedral}}$

$\ E_{\text{noncovalent}}=E_{\text{electrostatic}}+E_{\text{van der Waals}}$

Точная функциональная форма потенциальной функции или силового поля зависит от конкретной используемой программы моделирования. Обычно члены связи и угла моделируются как гармонические потенциалы, сосредоточенные вокруг равновесных значений длины связи, полученных в результате экспериментов или теоретических расчетов электронной структуры, выполненных с помощью программного обеспечения, которое выполняет расчеты типа ab-initio , например Gaussian . Для точного воспроизведения колебательных спектров потенциал Морса вместо этого можно использовать , требующий вычислительных затрат. Двугранные или крутильные члены обычно имеют несколько минимумов и, следовательно, не могут быть смоделированы как гармонические осцилляторы, хотя их конкретная функциональная форма варьируется в зависимости от реализации. Этот класс терминов может включать неправильные диэдральные термины, которые действуют как поправочные коэффициенты для отклонений от плоскости (например, их можно использовать для сохранения планарности бензольных колец или для исправления геометрии и киральности тетраэдрических атомов в представлении объединенного атома). ).

Полное вычисление несвязанных членов гораздо более затратно в вычислительном отношении, поскольку типичный атом связан лишь с несколькими своими соседями, но взаимодействует с каждым другим атомом в молекуле. К счастью, член Ван-дер-Ваальса быстро уменьшается. Обычно он моделируется с использованием 6–12 потенциала Леннарда-Джонса , что означает, что силы притяжения убывают с расстоянием по мере r. ⁻⁶ и силы отталкивания как r ⁻¹² , где r представляет расстояние между двумя атомами. Отталкивающая часть r ⁻¹² Однако это нефизично, поскольку отталкивание возрастает в геометрической прогрессии. Описание сил Ван-дер-Ваальса потенциалом Леннарда-Джонса 6–12 вносит неточности, которые становятся существенными на малых расстояниях. Обычно радиус обрезания используется для ускорения вычислений, чтобы пары атомов, расстояния которых превышают обрезание, имели энергию взаимодействия Ван-дер-Ваальса, равную нулю.

Электростатические члены, как известно, трудно хорошо вычислить, поскольку они не уменьшаются быстро с расстоянием, а дальнодействующие электростатические взаимодействия часто являются важными особенностями изучаемой системы (особенно для белков ). Основной функциональной формой является кулоновский потенциал , который падает только при изменении r ⁻¹ . Для решения этой проблемы используются различные методы, самым простым из которых является радиус обрезания, аналогичный тому, который используется для членов Ван-дер-Ваальса. Однако это приводит к резкому разрыву между атомами внутри и снаружи радиуса. Функции переключения или масштабирования, которые модулируют кажущуюся электростатическую энергию, являются несколько более точными методами, которые умножают рассчитанную энергию на плавно изменяющийся масштабный коэффициент от 0 до 1 на внешнем и внутреннем радиусах отсечки. Другими более сложными, но требующими больших вычислительных затрат методами являются сетка частиц Эвальда (PME) и алгоритм мультиполя .

В дополнение к функциональной форме каждого энергетического члена полезной энергетической функции должны быть присвоены параметры силовых констант, множителей Ван-дер-Ваальса и других постоянных членов. Эти термины вместе с равновесной связью, углами и значениями двугранников, значениями частичных зарядов, атомными массами и радиусами, а также определениями энергетической функции вместе называются силовым полем . Параметризация обычно осуществляется путем согласования экспериментальных значений и результатов теоретических расчетов. Силовое поле Нормана Л. Аллинджера в последней версии MM4 рассчитано для углеводородов, теплоты образования со среднеквадратичной погрешностью 0,35 ккал/моль, колебательные спектры со среднеквадратичной погрешностью 24 см. ⁻¹ , вращательные барьеры со среднеквадратичной ошибкой 2,2°, длинами связей CC в пределах 0,004 Å и углами CCC в пределах 1°. Более поздние версии MM4 охватывают также соединения с гетероатомами, такие как алифатические амины.

Каждое силовое поле параметризовано так, чтобы быть внутренне согласованным, но параметры обычно не переносятся из одного силового поля в другое.

Области применения

Основное применение молекулярной механики находится в области молекулярной динамики . При этом используется силовое поле для расчета сил, действующих на каждую частицу, и подходящий интегратор для моделирования динамики частиц и прогнозирования траекторий. При достаточной выборке и при условии соблюдения эргодической гипотезы траектории молекулярной динамики можно использовать для оценки термодинамических параметров системы или исследования кинетических свойств, таких как скорости и механизмы реакций.

Молекулярная механика также используется в QM/MM , что позволяет изучать кинетику белков и ферментов. Система разделена на две области, одна из которых обрабатывается с помощью квантовой механики (КМ), позволяющей разрывать и образовывать связи, а остальная часть белка моделируется с использованием молекулярной механики (ММ). Сама по себе ММ не позволяет изучить механизмы работы ферментов, что позволяет КМ. QM также обеспечивает более точный расчет энергии системы, хотя это гораздо дороже в вычислительном отношении.

Другое применение молекулярной механики — минимизация энергии, при которой силовое поле используется в качестве критерия оптимизации . Этот метод использует соответствующий алгоритм (например, наискорейший спуск ) для нахождения молекулярной структуры с локальным минимумом энергии. Эти минимумы соответствуют стабильным конформерам молекулы (в выбранном силовом поле), и движение молекулы можно моделировать как колебания вокруг этих стабильных конформеров и взаимопревращения между ними. Таким образом, часто встречаются методы минимизации локальной энергии в сочетании с глобальной оптимизацией энергии, чтобы найти глобальный минимум энергии (и другие состояния с низкой энергией). При конечной температуре молекула большую часть времени проводит в этих низколежащих состояниях, которые, таким образом, доминируют над молекулярными свойствами. Глобальная оптимизация может быть выполнена с помощью моделирования отжига , алгоритма Метрополиса и других методов Монте-Карло или с использованием различных детерминированных методов дискретной или непрерывной оптимизации. Хотя силовое поле представляет собой только энтальпийную составляющую свободной энергии составляющую можно (а при минимизации энергии учитывается только эта составляющая), включить энтропийную с помощью дополнительных методов, например анализа нормального режима .

Функции потенциальной энергии молекулярной механики использовались для расчета констант связи. кинетика сворачивания белка, протонационные равновесия, координаты активного сайта , и разработать сайты привязки .

Окружающая среда и решение

В молекулярной механике существует несколько способов определить среду, окружающую интересующую молекулу или молекулы. Систему можно смоделировать в вакууме (так называемое газофазное моделирование) без окружающей среды, но это обычно нежелательно, поскольку вносит артефакты в молекулярную геометрию, особенно в заряженные молекулы. Поверхностные заряды, которые обычно взаимодействуют с молекулами растворителя, вместо этого взаимодействуют друг с другом, создавая молекулярные конформации, которые вряд ли будут присутствовать в любой другой среде. Самый точный способ сольватировать систему — поместить явные молекулы воды в блок моделирования вместе с интересующими молекулами и рассматривать молекулы воды как взаимодействующие частицы, подобные частицам в других молекулах. Существует множество моделей воды с возрастающей сложностью, представляющих воду как простую твердую сферу (модель объединенного атома), как три отдельные частицы с фиксированным валентным углом или даже как четыре или пять отдельных центров взаимодействия для учета неспаренных электронов. на атоме кислорода. По мере того как модели воды становятся более сложными, соответствующие симуляции становятся более трудоемкими в вычислительном отношении. Компромиссный метод был найден в неявная сольватация , которая заменяет явно представленные молекулы воды математическим выражением, воспроизводящим среднее поведение молекул воды (или других растворителей, таких как липиды). Этот метод полезен для предотвращения артефактов, возникающих при моделировании вакуума, и хорошо воспроизводит свойства объемного растворителя, но не может воспроизвести ситуации, в которых отдельные молекулы воды создают специфические взаимодействия с растворенным веществом, которые плохо уловлены моделью растворителя, например, молекулы воды, которые часть сети водородных связей внутри белка.

Пакеты программного обеспечения

Основная статья: Сравнение программного обеспечения для моделирования молекулярной механики

Это ограниченный список; доступно гораздо больше пакетов.

• Морское ушко
• ACEMD - ГПУ MD
• ЯНТАРЬ
• Аскалаф Дизайнер
• БОСС
• ШАРММ
• КОСМОС
• CP2K
• Гемический
• ГРОМАКС
• ГРОМОС
• Внутренняя координатная механика (ICM)
• ЛАММПС
• Макромодель
• МДынаМикс
• Молекулярная операционная среда (MOE)
• НАМД
• вопрос
• Кью-Хим
• спартанский
• СтруММ3D (STR3DI32)
• Тинкер
• X-CRY
• Это осталось
• Зодиак

См. также

• Молекулярная графика
• Молекулярная динамика
• Редактор молекул
• Силовое поле (химия)
• Сравнение реализаций силового поля
• Программное обеспечение для молекулярного дизайна
• Молекулярное моделирование на GPU
• Сравнение программного обеспечения для моделирования молекулярной механики
• Список программного обеспечения для молекулярного моделирования Монте-Карло

Литература

• Аллингер Н.Л., Буркерт У (1982). Молекулярная механика . Публикация Американского химического общества. ISBN  978-0-8412-0885-8 .
• Коробка В.Г. (март 1997 г.). «Молекулярная механика квантованных валентных связей». Модель Дж Мол . 3 (3): 124–41. дои : 10.1007/s008940050026 . S2CID   93821090 .
• Вставка В.Г. (12 ноября 1998 г.). «Аномерный эффект моносахаридов и их производных. Результаты нового силового поля молекулярной механики QVBMM» . Гетероциклы . 48 (11): 2389–417. doi : 10.3987/REV-98-504 (неактивен 7 февраля 2024 г.). Архивировано из оригинала 31 мая 2012 года . Проверено 12 ноября 2008 г. {{cite journal}}: CS1 maint: DOI неактивен по состоянию на февраль 2024 г. ( ссылка )
• Коробка В.Г. (2004). «Стереоэлектронные эффекты в полинуклеотидах и их двойных спиралях». Дж. Мол. Структурировать . 689 (1–2): 33–41. Бибкод : 2004JMoSt.689...33B . doi : 10.1016/j.molstruc.2003.10.019 .
• Беккер О.М. (2001). Вычислительная биохимия и биофизика . Нью-Йорк, штат Нью-Йорк: Марсель Деккер. ISBN  978-0-8247-0455-1 .
• Маккерелл А.Д. (октябрь 2004 г.). «Эмпирические силовые поля для биологических макромолекул: обзор и проблемы». J Comput Chem . 25 (13): 1584–604. дои : 10.1002/jcc.20082 . ПМИД   15264253 . S2CID   9162620 .
• Шлик Т. (2002). Молекулярное моделирование и симуляция: междисциплинарное руководство . Берлин: Шпрингер. ISBN  978-0-387-95404-2 .
• Кришнан Намбури; Рамачандран, Канзас; Дипа Гопакумар (2008). Вычислительная химия и молекулярное моделирование: принципы и приложения . Берлин: Шпрингер. ISBN  978-3-540-77302-3 .

Внешние ссылки

• Пересмотр методов моделирования молекулярной динамики
• Молекулярная механика - это просто