Магнитохимия

Магнитохимия занимается изучением магнитных свойств химических соединений . Магнитные свойства возникают из-за спина и орбитального углового момента электронов, содержащихся в соединении. Соединения диамагнитны, если они не содержат неспаренных электронов . Молекулярные соединения, содержащие один или несколько неспаренных электронов, являются парамагнитными . Величина парамагнетизма выражается как эффективный магнитный момент μ _eff . первого ряда Для переходных металлов величина μ _eff в первом приближении является простой функцией количества неспаренных электронов (формула только для спина). В общем, спин-орбитальное взаимодействие приводит к отклонению μ _eff от формулы только для спина. Для более тяжелых переходных металлов, лантаноидов и актинидов , нельзя игнорировать спин-орбитальное взаимодействие. Обменное взаимодействие может происходить в кластерах и бесконечных решетках, что приводит к ферромагнетизму , антиферромагнетизму или ферримагнетизму в зависимости от взаимной ориентации отдельных спинов.

Магнитная восприимчивость [ править ]

Основным измерением в магнитохимии является магнитная восприимчивость. Это измеряет силу взаимодействия при помещении вещества в магнитное поле. Объемная магнитная восприимчивость , обозначаемая символом $\chi _{v}$ определяется отношением

{\vec {M}}=\chi _{v}{\vec {H}}

где, ${\vec {M}}$ - намагниченность материала ( магнитный дипольный момент на единицу объема), измеряемая в амперах на метр ( единицы СИ ), и ${\vec {H}}$ — напряженность магнитного поля , также измеряемая в амперах на метр. Восприимчивость – безразмерная величина . Для химических применений молярная магнитная восприимчивость (χ _моль предпочтительной величиной является ). Измеряется в м ³·моль ⁻¹ (СИ) или см ³·моль ⁻¹ (CGS) и определяется как

\chi _{\text{mol}}=M\chi _{v}/\rho

где ρ — плотность в кг·м ⁻³ (СИ) или г·см ⁻³ (CGS) и M — молярная масса в кг·моль. ⁻¹ (СИ) или г·моль ⁻¹ (ЦГС).

Существует множество методов измерения магнитной восприимчивости.

С помощью весов Гуи изменение веса образца измеряется с помощью аналитических весов , когда образец помещается в однородное магнитное поле. Измерения калибруются по известному стандарту, например, по тиоцианату ртути-кобальта HgCo(NCS) ₄ . Калибровка устраняет необходимость знать плотность образца. Измерения переменной температуры можно проводить, помещая образец в криостат между полюсными наконечниками магнита. ^[1]
Баланс Эванса . ^[2] представляет собой торсионные весы , в которых образец находится в фиксированном положении, а переменный вторичный магнит возвращает магниты в исходное положение. Он также калибруется по HgCo(NCS) ₄ .
С помощью весов Фарадея образец помещают в магнитное поле постоянного градиента и взвешивают на крутильных весах. Этот метод может дать информацию о магнитной анизотропии . ^[3]
СКВИД — очень чувствительный магнитометр.
Для веществ в растворе ЯМР можно использовать для измерения чувствительности. ^[4]^[5]

Типы магнитного поведения [ править ]

Когда изолированный атом помещается в магнитное поле, происходит взаимодействие, поскольку каждый электрон в атоме ведет себя как магнит, то есть электрон обладает магнитным моментом . Существует два типа взаимодействия.

Диамагнетизм. Помещенный в магнитное поле атом становится магнитно поляризованным, то есть у него появляется индуцированный магнитный момент. Сила взаимодействия стремится вытолкнуть атом из магнитного поля. По соглашению диамагнитной восприимчивости присваивается отрицательный знак. Очень часто диамагнитные атомы не имеют неспаренных электронов , т.е. каждый электрон спарен с другим электроном на той же атомной орбитали . Моменты двух электронов компенсируют друг друга, поэтому атом не имеет чистого магнитного момента. Однако для иона Eu ³⁺ у которого есть шесть неспаренных электронов, орбитальный угловой момент уравновешивает угловой момент электрона, и этот ион диамагнитен при нуле Кельвина.
Парамагнетизм. По крайней мере один электрон не спарен с другим. Атом обладает постоянным магнитным моментом. Помещенный в магнитное поле, атом притягивается к этому полю. По соглашению парамагнитной восприимчивости присваивается положительный знак.

Когда атом присутствует в химическом соединении, его магнитное поведение изменяется в зависимости от химического окружения. Измерение магнитного момента может дать полезную химическую информацию.

В некоторых кристаллических материалах отдельные магнитные моменты могут быть совмещены друг с другом (магнитный момент имеет как величину, так и направление). Это приводит к ферромагнетизму , антиферромагнетизму или ферримагнетизму . Это свойства кристалла в целом, мало влияющие на химические свойства.

Диамагнетизм [ править ]

Диамагнетизм — универсальное свойство химических соединений, поскольку все химические соединения содержат электронные пары. Соединение, в котором нет неспаренных электронов, называется диамагнитным. Эффект слабый, поскольку зависит от величины индуцированного магнитного момента. Это зависит от числа электронных пар и химической природы атомов, которым они принадлежат. таблицу «диамагнитных вкладов» или констант Паскаля . Это означает, что эффекты аддитивны, и можно составить ^[6]^[7]^[8] В случае парамагнитных соединений наблюдаемую восприимчивость можно корректировать, добавляя к ней так называемую диамагнитную поправку, которая представляет собой диамагнитную восприимчивость, рассчитанную по значениям из таблицы. ^[9]

Парамагнетизм [ править ]

Механизм и температурная зависимость [ править ]

Изменение магнитной восприимчивости с температурой

Ион металла с одним неспаренным электроном, например Cu ²⁺, в координационном комплексе дает простейшую иллюстрацию механизма парамагнетизма. Отдельные ионы металлов удерживаются лигандами на большом расстоянии друг от друга, поэтому между ними нет магнитного взаимодействия. Говорят, что система магнитно-разбавленная. Магнитные диполи атомов направлены в случайных направлениях. При приложении магнитного поля зеемановское расщепление происходит первого порядка. Атомов со спинами, ориентированными по полю, немного больше, чем атомов с неориентированными спинами. В эффекте Зеемана первого порядка разница энергий между двумя состояниями пропорциональна напряженности приложенного поля. Обозначая разницу энергий как Δ E , распределение Больцмана дает соотношение двух популяций как $e^{-\Delta E/kT}$ , где k — постоянная Больцмана , а T — температура в кельвинах . В большинстве случаев Δ E намного меньше kT , и экспоненту можно разложить до 1 – Δ E/kT . Из наличия в этом выражении 1/ Т следует , что восприимчивость обратно пропорциональна температуре. ^[10]

\chi ={C \over T}

Это известно как закон Кюри , а константа пропорциональности C известна как константа Кюри , значение которой для молярной восприимчивости рассчитывается как ^[11]

C={\frac {Ng^{2}S(S+1)\mu _{B}^{2}}{3k}}

где N — постоянная Авогадро , g — g-фактор Ланде , а μ _B — магнетон Бора . В этой трактовке предполагалось, что основное электронное состояние не вырождено, что магнитная восприимчивость обусловлена только спином электрона и что только основное состояние является термически заселенным.

Некоторые вещества подчиняются закону Кюри, другие подчиняются закону Кюри-Вейсса .

\chi ={\frac {C}{T-T_{c}}}

T _c – температура Кюри . Закон Кюри-Вейсса будет применяться только тогда, когда температура значительно превышает температуру Кюри. При температурах ниже температуры Кюри вещество может стать ферромагнитным . Более сложное поведение наблюдается с более тяжелыми переходными элементами.

Эффективный магнитный момент [ править ]

При соблюдении закона Кюри произведение молярной восприимчивости и температуры остается постоянным. Тогда эффективный магнитный момент , μ _eff определяется ^[12] как

\mu _{\text{eff}}=\mathrm {constant} {\sqrt {T\chi }}

Где C имеет единицы CGS см ³ моль ⁻¹ , _µэффK

\mu _{\text{eff}}={\sqrt {3k \over N\mu _{B}^{2}}}{\sqrt {T\chi }}\approx 2.82787{\sqrt {T\chi }}

Где C имеет единицы СИ м ³ моль ⁻¹ , _µэффK

\mu _{\text{eff}}={\sqrt {3k \over N\mu _{0}\mu _{B}^{2}}}{\sqrt {T\chi }}\approx 797.727{\sqrt {T\chi }}

Величина μ _eff фактически безразмерна, но часто выражается в единицах магнетона Бора (μ _B ). ^[12]

Для веществ, подчиняющихся закону Кюри, эффективный магнитный момент не зависит от температуры. Для других веществ µ _эфф зависит от температуры, но эта зависимость мала, если выполняется закон Кюри-Вейсса и температура Кюри мала.

парамагнетизм Независимый от температуры

Соединения, которые, как ожидается, будут диамагнитными, могут проявлять такой слабый парамагнетизм. Оно возникает из-за эффекта Зеемана второго порядка, при котором происходит дополнительное расщепление, пропорциональное квадрату напряженности поля. Это трудно наблюдать, поскольку соединение неизбежно также взаимодействует с магнитным полем в диамагнитном смысле. Тем не менее, имеются данные по перманганат- иону. ^[13] Это легче наблюдать в соединениях более тяжелых элементов, например в соединениях уранила .

Взаимодействие по обмену [ править ]

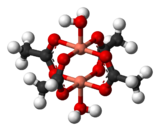
Ферримагнитное упорядочение в 2 измерениях

Антиферромагнитное упорядочение в 2 измерениях

Обменные взаимодействия возникают, когда вещество не магнитно разбавлено и имеются взаимодействия между отдельными магнитными центрами. Одной из простейших систем, проявляющих результат обменных взаимодействий, является кристаллический ацетат меди(II) Cu ₂ (OAc) ₄ (H ₂ O) ₂ . Как видно из формулы, он содержит два иона меди(II). Cu ²⁺ Ионы удерживаются вместе четырьмя ацетатными лигандами, каждый из которых связывается с обоими ионами меди. Каждый Cu ²⁺ у ion есть реклама ⁹ электронная конфигурация, поэтому он должен иметь один неспаренный электрон. Если бы между ионами меди существовала ковалентная связь, электроны образовали бы пары, и соединение было бы диамагнитным. Вместо этого происходит обменное взаимодействие, при котором спины неспаренных электронов частично выравниваются друг с другом. Фактически создаются два состояния: одно с параллельными спинами, а другое с противоположными спинами. Разница в энергии между двумя состояниями настолько мала, что их численность значительно меняется в зависимости от температуры. В результате магнитный момент изменяется с температурой по сигмоидальному закону. Состояние с противоположными спинами имеет меньшую энергию, поэтому взаимодействие в этом случае можно отнести к антиферромагнитному. ^[14] Считается, что это пример сверхобмена , опосредованного атомами кислорода и углерода ацетатных лигандов. ^[15] Другие димеры и кластеры проявляют обменное поведение. ^[16]

Обменные взаимодействия могут действовать на бесконечные цепочки в одном измерении, на плоскости в двух измерениях или на весь кристалл в трех измерениях. Это примеры дальнего магнитного упорядочения. Они порождают ферромагнетизм , антиферромагнетизм или ферримагнетизм , в зависимости от природы и взаимной ориентации отдельных спинов. ^[17]

Соединения при температурах ниже температуры Кюри обладают дальним магнитным порядком в виде ферромагнетизма. Другая критическая температура — температура Нееля , ниже которой возникает антиферромагнетизм. Шестигидрат хлорида никеля NiCl ₂ ·6H ₂ O имеет температуру Нееля 8,3 К. При этой температуре восприимчивость максимальна. Ниже температуры Нееля восприимчивость уменьшается и вещество становится антиферромагнитным. ^[18]

Комплексы ионов переходных металлов [ править ]

Эффективный магнитный момент соединения, содержащего ион переходного металла с одним или несколькими неспаренными электронами, зависит от общего орбитального и спинового углового момента неспаренных электронов: ${\vec {L}}$ и ${\vec {S}}$ , соответственно. «Итого» в данном контексте означает « векторная сумма ». В приближении, когда электронные состояния ионов металлов определяются связью Рассела-Сондерса и что спин-орбитальная связь пренебрежимо мала, магнитный момент определяется выражением ^[19]

\mu _{\text{eff}}={\sqrt {{\vec {L}}({\vec {L}}+1)+4{\vec {S}}({\vec {S}}+1)}}\mu _{B}

Формула только для вращения [ править ]

Орбитальный угловой момент генерируется, когда электрон на орбитали вырожденного набора орбиталей перемещается на другую орбиталь в наборе путем вращения. В комплексах низкой симметрии некоторые повороты невозможны. В этом случае говорят, что орбитальный угловой момент «погашен» и ${\vec {L}}$ меньше, чем можно было бы ожидать (частичное гашение), или равно нулю (полное гашение). Полное тушение наблюдается в следующих случаях. Заметим, что электрон в вырожденной паре d _{x ²-и ²} или д _{з ²} орбитали не могут вращаться в другую орбиталь из-за симметрии. ^[20]

Погашенный орбитальный угловой момент
д ^н	Октаэдрический			Тетраэдрический
д ^н		высокоспиновый	низкоспиновый
д ¹				и ¹
д ²				и ²
д ³	т _2г³
д ⁴		т _2г³например _г¹
д ⁵		т _2г³например _г²
д ⁶			т _2г⁶	и ³т ₂³
д ⁷			т _2г⁶например _г¹	и ⁴т ₂³
д ⁸	т _2г⁶например _г²
д ⁹	т _2г⁶например _г³

легенда: t _2g , t ₂ = (d _xy , d _xz , d _yz ). е _г , е знак равно (d _{x ²-и ²}, д _{з ²}).

Когда орбитальный угловой момент полностью погашен, ${\vec {L}}=0$ и парамагнетизм можно объяснить только спином электрона. Полный спиновый угловой момент составляет просто половину числа неспаренных электронов, и в результате получается формула только для спина.

\mu _{\text{eff}}={\sqrt {n(n+2)}}\mu _{B}

где n — число неспаренных электронов. Формула только спина является хорошим первым приближением для высокоспиновых комплексов переходных металлов первого ряда . ^[21]

Ион	Количество непарный электроны	Только вращение момент / _мкБ	наблюдал момент / _мкБ
Из ³⁺	1	1.73	1.73
V ⁴⁺	1	1.73	1.68–1.78
С ²⁺	1	1.73	1.70–2.20
V ³⁺	2	2.83	2.75–2.85
В ²⁺	2	2.83	2.8–3.5
V ²⁺	3	3.87	3.80–3.90
Кр ³⁺	3	3.87	3.70–3.90
Ко ²⁺	3	3.87	4.3–5.0
Мин. ⁴⁺	3	3.87	3.80–4.0
Кр ²⁺	4	4.90	4.75–4.90
Фе ²⁺	4	4.90	5.1–5.7
Мин. ²⁺	5	5.92	5.65–6.10
Фе ³⁺	5	5.92	5.7–6.0

Небольшие отклонения от формулы только для спина могут быть результатом пренебрежения орбитальным угловым моментом или спин-орбитальным взаимодействием. Например, тетраэдр d ³, д ⁴, д ⁸ и д ⁹ комплексы имеют тенденцию демонстрировать большие отклонения от формулы только спина, чем октаэдрические комплексы того же иона, поскольку «гашение» орбитального вклада менее эффективно в тетраэдрическом случае. ^[22]

Низкоспиновые комплексы [ править ]

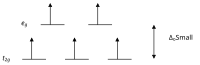
Согласно теории кристаллического поля, d -орбитали иона переходного металла в октаэдрическом комплексе расщепляются на две группы в кристаллическом поле. Если расщепление достаточно велико, чтобы преодолеть энергию, необходимую для помещения электронов на одну и ту же орбиталь с противоположным спином, в результате образуется низкоспиновый комплекс.

Высоко- и низкоспиновые октаэдрические комплексы
d-счет	Количество неспаренных электронов		примеры
d-счет	высокоспиновый	низкоспиновый	примеры
д ⁴	4	2	Кр ²⁺, Мн ³⁺
д ⁵	5	1	Мин. ²⁺, Фе ³⁺
д ⁶	4	0	Фе ²⁺, Ко ³⁺
д ⁷	3	1	Ко ²⁺

При одном неспаренном электроне значения µ _eff составляют от 1,8 до 2,5 _µB , а при двух неспаренных электронах - от 3,18 до 3,3 _µB . Отметим, что низкоспиновые комплексы Fe ²⁺ и Ко ³⁺ являются диамагнитными. Другая группа диамагнитных комплексов — это плоскоквадратные комплексы d ⁸ ионы, такие как Ni ²⁺ и резус ⁺ и Ау ³⁺.

Спин-кроссовер [ править ]

Когда разность энергий между высокоспиновым и низкоспиновым состояниями сравнима с kT ( k - постоянная Больцмана , а T - температура), между спиновыми состояниями устанавливается равновесие, включающее так называемые «электронные изомеры». Трисдитиокарбамато 2 железа(III), Fe(S ₃ CNR ₂ ) _. , является хорошо документированным примером Эффективный момент варьируется от типичного d ⁵ низкоспиновое значение от 2,25 _мкБ при 80 К до более 4 _мкБ выше 300 К. ^[23]

Переходные металлы 2-го и 3 ряда - го

Расщепление кристаллического поля больше для комплексов более тяжелых переходных металлов, чем для переходных металлов, обсуждавшихся выше. Следствием этого является то, что низкоспиновые комплексы встречаются гораздо чаще. Константы спин-орбитального взаимодействия ζ также больше, и их нельзя игнорировать даже при элементарных подходах. Магнитное поведение было обобщено, как показано ниже, вместе с обширной таблицей данных. ^[24]

d-счет	кТ/ζ=0,1 μ _эфф	кТ/ζ=0 μ _эфф	Поведение при большой константе спин-орбитального взаимодействия ζ _nd
д ¹	0.63	0	μ _eff меняется в зависимости от T ^1/2
д ²	1.55	1.22	μ _eff меняется в зависимости от T, примерно
д ³	3.88	3.88	Независимость от температуры
д ⁴	2.64	0	μ _eff меняется в зависимости от T ^1/2
д ⁵	1.95	1.73	μ _eff меняется в зависимости от T, примерно

Лантаниды и актиниды [ править ]

Связь Рассела-Сондерса , LS-связь, применима к ионам лантаноидов, эффектами кристаллического поля можно пренебречь, но спин-орбитальной связью нельзя пренебречь. Следовательно, спиновые и орбитальные угловые моменты должны быть объединены.

{\vec {L}}=\sum _{i}{\vec {l}}_{i}

{\vec {S}}=\sum _{i}{\vec {s}}_{i}

{\vec {J}}={\vec {L}}+{\vec {S}}

а рассчитанный магнитный момент равен

\mu _{\text{eff}}=g{\sqrt {{\vec {J}}({\vec {J}}+1)}};g={3 \over 2}+{\frac {{\vec {S}}({\vec {S}}+1)-{\vec {L}}({\vec {L}}+1)}{2{\vec {J}}({\vec {J}}+1)}}

Магнитные свойства соединений трехвалентных лантаноидов ^[25]
лантаноид	Этот	Пр	Нд	вечера	см	Евросоюз	Б-г	Тб	Те	К	Является	Тм	Ыб
Количество неспаренных электронов	1	2	3	4	5	6	7	6	5	4	3	2	1
расчетный момент / _мкБ	2.54	3.58	3.62	2.68	0.85	0	7.94	9.72	10.65	10.6	9.58	7.56	4.54
наблюдаемый момент /μ _B	2.3–2.5	3.4–3.6	3.5–3.6		1.4–1.7	3.3–3.5	7.9–8.0	9.5–9.8	10.4–10.6	10.4–10.7	9.4–9.6	7.1–7.5	4.3–4.9

В актинидах спин-орбитальная связь сильная и приближается к j j -связи.

{\vec {J}}=\sum _{i}{\vec {j}}_{i}=\sum _{i}({\vec {l}}_{i}+{\vec {s}}_{i})

Это означает, что трудно рассчитать эффективный момент. Например, уран(IV), f ², в комплексе [UCl ₆ ] ²⁻ имеет измеренный эффективный момент 2,2 мкм _B , который включает вклад независимого от температуры парамагнетизма. ^[26]

Элементы основной группы и органические соединения [ править ]

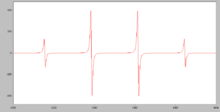
Очень немногие соединения элементов основной группы являются парамагнитными. Известные примеры включают: кислород , O ₂ ; оксид азота , NO; диоксид азота NO ₂ и диоксид хлора ClO ₂ . В органической химии соединения с неспаренным электроном называются свободными радикалами . Свободные радикалы, за некоторыми исключениями, недолговечны, поскольку один свободный радикал быстро реагирует с другим, поэтому их магнитные свойства трудно изучать. Однако если радикалы хорошо отделены друг от друга в разбавленном растворе в твердой матрице, то при низкой температуре их можно изучать методом электронного парамагнитного резонанса (ЭПР). Такие радикалы образуются при облучении. Обширные исследования ЭПР многое рассказали о делокализации электронов в свободных радикалах. Смоделированный спектр радикала CH ₃ • демонстрирует сверхтонкое расщепление вследствие взаимодействия электрона с тремя эквивалентными ядрами водорода, каждое из которых имеет спин 1/2. ^[27]^[28]

Спиновые метки представляют собой долгоживущие свободные радикалы, которые можно внедрять в органические молекулы, чтобы их можно было изучать методом ЭПР. ^[29] Например, нитроксид MTSL , функционализированное производное TEtra метилпиперидиноксида, TEMPO , используется в сайт-направленном спин-мечении .

Приложения [ править ]

Ион гадолиния , Gd ³⁺, имеет f ⁷ электронная конфигурация, в которой все спины параллельны. Соединения Б-га ³⁺ ионы наиболее подходят для использования в качестве контрастного вещества при МРТ . ^[30] Магнитные моменты соединений гадолиния больше, чем у любого иона переходного металла. Гадолинийпредпочтительнее других ионов лантаноидов, некоторые из которых имеют более высокие эффективные моменты, из-за того, что они имеют невырожденное основное электронное состояние . ^[31]

В течение многих лет природа оксигемоглобина Hb -O ₂ оставалась весьма спорной. Экспериментально было обнаружено, что он диамагнитен. Принято считать, что дезоксигемоглобин представляет собой комплекс железа в степени окисления +2 , т.е. ⁶ система с высокоспиновым магнитным моментом, близким к только спиновому значению 4,9 мкм _B . Было высказано предположение, что железо окисляется, а кислород восстанавливается до супероксида.

Fe(II)Hb (высокоспиновый) + O ₂ ⇌ [Fe(III)Hb]O ₂⁻

Спаривание электронов из Fe ³⁺ и О ₂⁻ Тогда было предложено осуществить это посредством механизма обмена. Теперь было показано, что на самом деле железо(II) меняется с высокоспинового на низкоспиновое, когда молекула кислорода отдает пару электронов железу. Если в дезоксигемоглобине атом железа лежит выше плоскости гема, то в низкоспиновом комплексе эффективный ионный радиус уменьшен и атом железа лежит в плоскости гема. ^[32]

Fe(II)Hb + O ₂ ⇌ [Fe(II)Hb]O ₂ (низкоспиновый)

Эта информация имеет важное значение для исследований по поиску искусственных переносчиков кислорода .

Соединения галлия(II) до недавнего времени были неизвестны. Поскольку атомный номер галлия нечетное число (31), Ga ²⁺ должен иметь неспаренный электрон. Предполагалось, что он будет действовать как свободный радикал и иметь очень короткое время жизни. Отсутствие соединений Ga(II) было частью так называемого эффекта инертной пары . Когда соли аниона с брутто-формулой, например [GaCl ₃ ] ⁻ были синтезированы, они оказались диамагнитными. Это подразумевало образование связи Ga-Ga и димерной формулы [Ga ₂ Cl ₆ ] ²⁻. ^[33]

См. также [ править ]

Ссылки [ править ]

^ Эрншоу, с. 89
^ Балансы магнитной восприимчивости
^ О'Коннор, CJ (1982). Липпард, С.Дж. (ред.). Измерения магнитной восприимчивости . Прогресс неорганической химии. Том. 29. Уайли. п. 203. ИСБН 978-0-470-16680-2 .
^ Эванс, Д.Ф. (1959). «Определение парамагнитной восприимчивости веществ в растворах методом ядерного магнитного резонанса». Дж. Хим. Соц. : 2003–2005 гг. дои : 10.1039/JR9590002003 .
^ Орчард, с. 15. Эрншшоу, с. 97
^ Фиггис и Льюис, с. 403
^ Карлин, с. 3
^ Бэйн, Гордон А.; Берри, Джон Ф. (2008). «Диамагнитные поправки и константы Паскаля». Дж. Хим. Образование . 85 (4): 532. Бибкод : 2008JChEd..85..532B . дои : 10.1021/ed085p532 .
^ Фиггис и Льюис, с. 417
^ Фиггис и Льюис, с. 419
^ Орчард, с. 48
↑ Перейти обратно: Перейти обратно: ^а ^б Хоппе, Дж.И. (1972). «Эффективный магнитный момент». Дж. Хим. Образование . 49 (7): 505. Бибкод : 1972JChEd..49..505H . дои : 10.1021/ed049p505 .
^ Орчард, с. 53
↑ Перейти обратно: Перейти обратно: ^а ^б Лоуренс Ку (март 2000 г.). Физические методы в бионеорганической химии: спектроскопия и магнетизм . Университетские научные книги. стр. 345–348. ISBN 978-1-891389-02-3 . Проверено 22 февраля 2011 г.
^ Фиггис и Льюис, с. 435. Фруктовый сад, с. 67
^ Карлин, разделы 5.5–5.7
^ Карлин, главы 6 и 7, стр. 112–225.
^ Карин, стр. 264.
^ Фиггис и Льюис, с. 420
^ Фиггис и Льюис, стр. 424, 432
^ Фиггис и Льюис, с. 406
^ Фиггис и Льюис, Раздел 3, «Орбитальный вклад»
^ Орчард, с. 125. Карлин, с. 270
^ Фиггис и Льюис, стр. 443–451
^ Гринвуд и Эрншоу, с. 1243
^ Орчард, с. 106
^ Вейл, Джон А.; Болтон, Джеймс Р.; Вертц, Джон Э. (1994). Электронный парамагнитный резонанс: элементарная теория и практические приложения . Уайли. ISBN 0-471-57234-9 .
^ Аткинс, П.В.; Саймонс, MCR (1967). Строение неорганических радикалов; применение электронного спинового резонанса к изучению молекулярной структуры . Эльзевир.
^ Берлинер, ЖЖ (1976). Спиновая маркировка: теория и приложения I. Академическая пресса. ISBN 0-12-092350-5 . Берлинер, ЖЖ (1979). Спиновая маркировка II: теория и приложения . Академическая пресса. ISBN 0-12-092352-1 .
^ Краузе, В. (2002). Контрастные вещества I: Магнитно-резонансная томография: Pt. 1 . Спрингер. ISBN 3540422471 .
^ Караван, Питер; Эллисон, Джеффри Дж.; Макмерри, Томас Дж.; Лауффер, Рэндалл Б., Джеффри Дж.; Макмерри, Томас Дж.; Лауффер, Рэндалл Б. (1999). «Хелаты гадолиния (III) как контрастные вещества для МРТ: структура, динамика и применение». хим. Преподобный . 99 (9): 2293–2352. дои : 10.1021/cr980440x . ПМИД 11749483 . {{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )
^ Гринвуд и Эрншоу, стр. 1099–1011.
^ Гринвуд и Эрншоу, с. 240

Библиография [ править ]

Карлин, Р.Л. (1986). Магнитохимия . Спрингер . ISBN 978-3-540-15816-5 .
Эрншоу, Алан (1968). Введение в магнитохимию . Академическая пресса .
Фиггис, Б.Н.; Льюис, Дж. (1960). «Магнитохимия сложных соединений». В Льюисе. Дж. и Уилкинс. РГ (ред.). Современная координационная химия . Нью-Йорк: Уайли .
Гринвуд, Норман Н .; Эрншоу, Алан (1997). Химия элементов (2-е изд.). Баттерворт-Хайнеманн . ISBN 978-0-08-037941-8 .
Орчард, AF (2003). Магнитохимия . Оксфордские учебники по химии. Издательство Оксфордского университета . ISBN 0-19-879278-6 .
Селвуд, военнопленный (1943). Магнитохимия . Издательство Интерсайенс, Инк.
Вульфсон, Сергей (1998). Молекулярная магнитохимия . Тейлор и Фрэнсис . ISBN 90-5699-535-9 .

Внешние ссылки [ править ]

[1] Эрншоу, с. 89

[2] Балансы магнитной восприимчивости

[3] О'Коннор, CJ (1982). Липпард, С.Дж. (ред.). Измерения магнитной восприимчивости . Прогресс неорганической химии. Том. 29. Уайли. п. 203. ИСБН 978-0-470-16680-2 .

[4] Эванс, Д.Ф. (1959). «Определение парамагнитной восприимчивости веществ в растворах методом ядерного магнитного резонанса». Дж. Хим. Соц. : 2003–2005 гг. дои : 10.1039/JR9590002003 .

[5] Орчард, с. 15. Эрншшоу, с. 97

[6] Фиггис и Льюис, с. 403

[7] Карлин, с. 3

[8] Бэйн, Гордон А.; Берри, Джон Ф. (2008). «Диамагнитные поправки и константы Паскаля». Дж. Хим. Образование . 85 (4): 532. Бибкод : 2008JChEd..85..532B . дои : 10.1021/ed085p532 .

[9] Фиггис и Льюис, с. 417

[10] Фиггис и Льюис, с. 419

[11] Орчард, с. 48

[HoppeJI-12] Перейти обратно: Перейти обратно: ^а ^б Хоппе, Дж.И. (1972). «Эффективный магнитный момент». Дж. Хим. Образование . 49 (7): 505. Бибкод : 1972JChEd..49..505H . дои : 10.1021/ed049p505 .

[13] Орчард, с. 53

[b1-14] Перейти обратно: Перейти обратно: ^а ^б Лоуренс Ку (март 2000 г.). Физические методы в бионеорганической химии: спектроскопия и магнетизм . Университетские научные книги. стр. 345–348. ISBN 978-1-891389-02-3 . Проверено 22 февраля 2011 г.

[15] Фиггис и Льюис, с. 435. Фруктовый сад, с. 67

[16] Карлин, разделы 5.5–5.7

[17] Карлин, главы 6 и 7, стр. 112–225.

[18] Карин, стр. 264.

[19] Фиггис и Льюис, с. 420

[20] Фиггис и Льюис, стр. 424, 432

[21] Фиггис и Льюис, с. 406

[22] Фиггис и Льюис, Раздел 3, «Орбитальный вклад»

[23] Орчард, с. 125. Карлин, с. 270

[24] Фиггис и Льюис, стр. 443–451

[25] Гринвуд и Эрншоу, с. 1243

[26] Орчард, с. 106

[27] Вейл, Джон А.; Болтон, Джеймс Р.; Вертц, Джон Э. (1994). Электронный парамагнитный резонанс: элементарная теория и практические приложения . Уайли. ISBN 0-471-57234-9 .

[28] Аткинс, П.В.; Саймонс, MCR (1967). Строение неорганических радикалов; применение электронного спинового резонанса к изучению молекулярной структуры . Эльзевир.

[29] Берлинер, ЖЖ (1976). Спиновая маркировка: теория и приложения I. Академическая пресса. ISBN 0-12-092350-5 . Берлинер, ЖЖ (1979). Спиновая маркировка II: теория и приложения . Академическая пресса. ISBN 0-12-092352-1 .

[30] Краузе, В. (2002). Контрастные вещества I: Магнитно-резонансная томография: Pt. 1 . Спрингер. ISBN 3540422471 .

[31] Караван, Питер; Эллисон, Джеффри Дж.; Макмерри, Томас Дж.; Лауффер, Рэндалл Б., Джеффри Дж.; Макмерри, Томас Дж.; Лауффер, Рэндалл Б. (1999). «Хелаты гадолиния (III) как контрастные вещества для МРТ: структура, динамика и применение». хим. Преподобный . 99 (9): 2293–2352. дои : 10.1021/cr980440x . ПМИД 11749483 . {{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )

[32] Гринвуд и Эрншоу, стр. 1099–1011.

[33] Гринвуд и Эрншоу, с. 240

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

v т и Магнетизм
Magnetic response	diamagnetism superdiamagnetism paramagnetism superparamagnetism Van Vleck paramagnetism
Magnetic states	altermagnetism antiferromagnetism ferrimagnetism ferromagnetism superferromagnetism ferromagnetic superconductor helimagnetism metamagnetism mictomagnetism spin glass amorphous magnetism spin ice

v т и Отрасли химии
Glossary of chemical formulae List of biomolecules List of inorganic compounds Periodic table
Analytical	Instrumental chemistry Electroanalytical methods Spectroscopy IR Raman UV-Vis NMR Mass spectrometry EI ICP MALDI Separation process Chromatography GC HPLC Crystallography Characterization Titration Wet chemistry Calorimetry Elemental analysis
Theoretical	Quantum chemistry Computational chemistry Mathematical chemistry Molecular modelling Molecular mechanics Molecular dynamics Molecular geometry VSEPR theory
Physical	Electrochemistry Spectroelectrochemistry Photoelectrochemistry Thermochemistry Chemical thermodynamics Surface science Interface and colloid science Micromeritics Cryochemistry Sonochemistry Structural chemistry Chemical physics Molecular physics Femtochemistry Chemical kinetics Spectroscopy Photochemistry Spin chemistry Microwave chemistry Equilibrium chemistry Mechanochemistry
Inorganic	Coordination chemistry Magnetochemistry Organometallic chemistry Organolanthanide chemistry Cluster chemistry Solid-state chemistry Ceramic chemistry
Organic	Stereochemistry Alkane stereochemistry Physical organic chemistry Organic reactions Organic synthesis Retrosynthetic analysis Enantioselective synthesis Total synthesis / Semisynthesis Fullerene chemistry Polymer chemistry Petrochemistry Dynamic covalent chemistry
Biological	Biochemistry Molecular biology Cell biology Chemical biology Bioorthogonal chemistry Medicinal chemistry Pharmacology Clinical chemistry Neurochemistry Bioorganic chemistry Bioorganometallic chemistry Bioinorganic chemistry Biophysical chemistry
Interdisciplinarity	Nuclear chemistry Radiochemistry Radiation chemistry Actinide chemistry Cosmochemistry / Astrochemistry / Stellar chemistry Geochemistry Biogeochemistry Photogeochemistry Environmental chemistry Atmospheric chemistry Ocean chemistry Clay chemistry Carbochemistry Food chemistry Carbohydrate chemistry Food physical chemistry Agricultural chemistry Soil chemistry Chemistry education Amateur chemistry General chemistry Clandestine chemistry Forensic chemistry Forensic toxicology Post-mortem chemistry Nanochemistry Supramolecular chemistry Chemical synthesis Green chemistry Click chemistry Combinatorial chemistry Biosynthesis Chemical engineering Stoichiometry Materials science Metallurgy Ceramic engineering Polymer science
See also	History of chemistry Nobel Prize in Chemistry Timeline of chemistry of element discoveries "The central science" Chemical reaction Catalysis Chemical element Chemical compound Atom Molecule Ion Chemical substance Chemical bond Alchemy Quantum mechanics
Category Commons Portal WikiProject

Базы данных авторитетного контроля
National	Germany Israel United States
Other	Encyclopedia of Modern Ukraine