Парамагнетизм

Парамагнетизм — это форма магнетизма , при которой некоторые материалы слабо притягиваются внешним магнитным полем и образуют внутренние индуцированные магнитные поля в направлении приложенного магнитного поля. В отличие от такого поведения, диамагнитные материалы отталкиваются магнитными полями и образуют индуцированные магнитные поля в направлении, противоположном направлению приложенного магнитного поля. ^[1] Парамагнитные материалы включают большинство химических элементов и некоторые соединения ; ^[2] они имеют относительную магнитную проницаемость немного больше 1 (т. е. небольшую положительную магнитную восприимчивость ) и, следовательно, притягиваются к магнитным полям. Магнитный момент, индуцированный приложенным полем, линеен по напряженности поля и достаточно слаб. Для обнаружения эффекта обычно требуются чувствительные аналитические весы, и современные измерения парамагнитных материалов часто проводятся с помощью СКВИДа магнитометра .

Парамагнетизм обусловлен наличием неспаренных электронов в материале , поэтому большинство атомов с неполностью заполненными атомными орбиталями являются парамагнитными, хотя существуют исключения, такие как медь. Из-за своего спина неспаренные электроны обладают магнитным дипольным моментом и действуют как крошечные магниты. Внешнее магнитное поле заставляет спины электронов выравниваться параллельно полю, вызывая суммарное притяжение. Парамагнитные материалы включают алюминий , кислород , титан и оксид железа (FeO). Поэтому в химии используется простое практическое правило, чтобы определить, является ли частица (атом, ион или молекула) парамагнитной или диамагнитной: ^[3] если все электроны в частице спарены, то вещество, состоящее из этой частицы, диамагнитно; если у него есть неспаренные электроны, то вещество парамагнитно.

В отличие от ферромагнетиков , парамагнетики не сохраняют намагниченность в отсутствие внешнего магнитного поля, поскольку тепловое движение хаотизирует ориентации спинов. (Некоторые парамагнетики сохраняют спиновый беспорядок даже при абсолютном нуле , что означает, что они парамагнитны в основном состоянии , то есть в отсутствие теплового движения.) Таким образом, общая намагниченность падает до нуля, когда приложенное поле удаляется. Даже в присутствии поля существует лишь небольшая индуцированная намагниченность, поскольку только небольшая часть спинов будет ориентирована полем. Эта доля пропорциональна напряженности поля и этим объясняется линейная зависимость. Притяжение, испытываемое ферромагнитными материалами, нелинейно и гораздо сильнее, поэтому его легко наблюдать, например, в притяжении между магнитом холодильника и железом самого холодильника.

со электронов Связь спинами

Парамагнетизм, ферромагнетизм и спиновые волны.

Составляющие атомы или молекулы парамагнетиков имеют постоянные магнитные моменты ( диполи ) даже в отсутствие приложенного поля. Постоянный момент обычно возникает из-за вращения неспаренных электронов на атомных или молекулярных электронных орбиталях (см. Магнитный момент ). В чистом парамагнетизме диполи не взаимодействуют друг с другом и ориентированы случайным образом в отсутствие внешнего поля из-за теплового возбуждения, что приводит к нулевому суммарному магнитному моменту. Когда приложено магнитное поле, диполи будут стремиться выровняться по направлению приложенного поля, в результате чего возникнет чистый магнитный момент в направлении приложенного поля. В классическом описании можно понимать, что это выравнивание происходит из-за крутящего момента , приложенного к магнитным моментам приложенным полем, которое пытается выровнять диполи параллельно приложенному полю. Однако истинные причины выравнивания можно понять только через квантово-механические свойства спина и углового момента .

Если между соседними диполями происходит достаточный обмен энергией, они будут взаимодействовать и могут спонтанно выровняться или развернуться и образовать магнитные домены, что приведет к ферромагнетизму (постоянные магниты) или антиферромагнетизму соответственно. Парамагнитное поведение можно также наблюдать в ферромагнетиках, температура которых выше температуры Кюри , и в антиферромагнетиках, температура которых выше температуры Нееля . При этих температурах доступная тепловая энергия просто превосходит энергию взаимодействия между спинами.

В целом парамагнитные эффекты весьма малы: магнитная восприимчивость порядка 10 ⁻³ до 10 ⁻⁵ для большинства парамагнетиков, но может достигать 10 ⁻¹ для синтетических парамагнетиков, таких как феррожидкости .

Делокализация [ править ]

Избранные парамагнитные металлы Паули. ^[4]
Материал	Магнитная восприимчивость, $\chi _{v}$ [10 ⁻⁵] (единицы СИ)
вольфрам	6.8
Цезий	5.1
Алюминий	2.2
Литий	1.4
Магний	1.2
Натрий	0.72

В проводящих материалах электроны делокализованы , то есть они перемещаются через твердое тело более или менее как свободные электроны . проводимость можно понимать В картине зонной структуры как возникающую из-за неполного заполнения энергетических зон.В обычном немагнитном проводнике зона проводимости одинакова для электронов как со спином вверх, так и со спином вниз. При приложении магнитного поля зона проводимости разделяется на зоны со спином вверх и со спином вниз из-за разницы в магнитной потенциальной энергии для электронов со спином вверх и вниз.Поскольку уровень Ферми должен быть одинаковым для обеих зон, это означает, что в зоне, сместившейся вниз, будет небольшой избыток того типа спина. Этот эффект представляет собой слабую форму парамагнетизма, известную как парамагнетизм Паули .

Эффект всегда конкурирует с диамагнитным откликом противоположного знака, обусловленным всеми остовными электронами атомов. Более сильные формы магнетизма обычно требуют локализованных, а не блуждающих электронов. Однако в некоторых случаях может возникнуть зонная структура, в которой имеются две делокализованные подзоны с состояниями противоположных спинов, имеющими разные энергии. Если одна подзона заполнена преимущественно над другой, может возникнуть коллективный ферромагнитный порядок. Такая ситуация обычно возникает только в относительно узких (d-)зонах, которые плохо делокализованы.

s и p-электроны [ править ]

Как правило, сильная делокализация в твердом теле из-за большого перекрытия с соседними волновыми функциями означает, что будет большая скорость Ферми ; это означает, что количество электронов в зоне менее чувствительно к изменениям энергии этой зоны, что подразумевает слабый магнетизм. Вот почему металлы s- и p-типа обычно либо парамагнитны Паули, либо, как в случае золота, даже диамагнитны. В последнем случае диамагнитный вклад внутренних электронов замкнутой оболочки просто преобладает над слабым парамагнитным членом почти свободных электронов.

d и f электроны [ править ]

Более сильные магнитные эффекты обычно наблюдаются только при участии d- или f-электронов. Особенно последние обычно сильно локализованы. Более того, размер магнитного момента на атоме лантаноида может быть довольно большим, поскольку в случае гадолиния (III) он может нести до 7 неспаренных электронов (отсюда и его использование в МРТ ). Высокие магнитные моменты, связанные с лантанидами, являются одной из причин, почему сверхсильные магниты обычно основаны на таких элементах, как неодим или самарий .

локализация Молекулярная

Приведенная выше картина является обобщением , поскольку она относится к материалам с расширенной решеткой, а не с молекулярной структурой. Молекулярная структура также может приводить к локализации электронов. Хотя обычно существуют энергетические причины, по которым молекулярная структура не имеет частично заполненных орбиталей (т.е. неспаренных спинов), некоторые фрагменты незамкнутой оболочки все же встречаются в природе. Молекулярный кислород является хорошим примером. Даже в замороженном твердом состоянии он содержит дирадикальные молекулы, что приводит к парамагнитному поведению. Неспаренные спины располагаются на орбиталях, полученных из p-волновых функций кислорода, но перекрытие ограничивается одним соседом в молекулах O ₂ . Расстояния до других атомов кислорода в решетке остаются слишком большими, чтобы привести к делокализации, и магнитные моменты остаются неспаренными.

Теория [ править ]

Теорема Бора-Ван Левена доказывает, что в чисто классической системе не может быть ни диамагнетизма, ни парамагнетизма. Тогда парамагнитный отклик имеет два возможных квантовых источника: либо из-за постоянных магнитных моментов ионов, либо из-за пространственного движения электронов проводимости внутри материала. Оба описания приведены ниже.

Закон Кюри [ править ]

При низких уровнях намагниченности намагниченность парамагнетиков следует так называемому закону Кюри , по крайней мере приблизительно. Этот закон указывает на то, что восприимчивость, $\chi$ , парамагнетиков обратно пропорциональна их температуре, т.е. материалы становятся более магнитными при более низких температурах. Математическое выражение: $\mathbf {M} =\chi \mathbf {H} ={\frac {C}{T}}\mathbf {H}$ где:

$\mathbf {M}$ результирующая намагниченность, измеряемая в амперах на метр (А/м),
$\chi$ – объемная магнитная восприимчивость ( безразмерная ),
$H$ – вспомогательное магнитное поле (А/м),
$T$ — абсолютная температура, измеряемая в кельвинах (К),
$C$ специфичная для материала . — константа Кюри (K),

Закон Кюри действителен в часто встречающихся условиях низкой намагниченности ( μ _B H ≲ k _B T ), но не применяется в режиме сильного поля/низкой температуры, когда происходит насыщение намагниченности ( μ _B H ≳ k _B T ). и все магнитные диполи ориентированы в направлении приложенного поля. Когда диполи выровнены, увеличение внешнего поля не приведет к увеличению общей намагниченности, поскольку дальнейшего выравнивания быть не может.

Для парамагнитного иона с невзаимодействующими магнитными моментами с угловым моментом J константа Кюри связана с магнитными моментами отдельных ионов: $C={\frac {n}{3k_{\mathrm {B} }}}\mu _{\mathrm {eff} }^{2}{\text{ where }}\mu _{\mathrm {eff} }=g_{J}\mu _{\mathrm {B} }{\sqrt {J(J+1)}}.$

где n — количество атомов в единице объема. Параметр µ _eff интерпретируется как эффективный магнитный момент, приходящийся на парамагнитный ион. Если использовать классическую трактовку с молекулярными магнитными моментами, представленными в виде дискретных магнитных диполей , то выражение закона Кюри той же формы появится с ц, появляющимся вместо ц _эфф .

Вывод

рассматривая вещество с невзаимодействующими магнитными моментами с угловым моментом J. Закон Кюри можно вывести , Если орбитальные вклады в магнитный момент пренебрежимо малы (частый случай), то в дальнейшем J = S . что мы решили назвать осью z , энергетические уровни каждого парамагнитного центра испытают зеемановское расщепление своих энергетических уровней, каждый из которых имеет z -компоненту, обозначенную M _J (или просто MS _{Если мы приложим магнитное поле вдоль того ,} для только спиновый магнитный случай). Применяя квазиклассическую статистику Больцмана , намагниченность такого вещества равна $n{\bar {m}}={\frac {n\sum \limits _{M_{J}=-J}^{J}{\mu _{M_{J}}e^{{-E_{M_{J}}}/{k_{\mathrm {B} }T}\;}}}{\sum \limits _{M_{J}=-J}^{J}{e^{{-E_{M_{J}}}/{k_{\mathrm {B} }T}\;}}}}={\frac {n\sum \limits _{M_{J}=-J}^{J}{M_{J}g_{J}\mu _{\mathrm {B} }e^{{M_{J}g_{J}\mu _{\mathrm {B} }H}/{k_{\mathrm {B} }T}\;}}}{\sum \limits _{M_{J}=-J}^{J}{e^{{M_{J}g_{J}\mu _{\mathrm {B} }H}/{k_{\mathrm {B} }T}\;}}}}.$

Где $\mu _{M_{J}}$ - z -компонента магнитного момента для каждого зеемановского уровня, поэтому $\mu _{M_{J}}=M_{J}g_{J}\mu _{\mathrm {B} }-\mu _{\mathrm {B} }$ называется магнетоном Бора , а g _J — это g-фактор Ланде , который сводится к g-фактору свободных электронов g _S когда J = S. , (в этой трактовке мы предполагаем, что x- и y -компоненты намагниченности, усредненные по всем молекулам, сокращаются, поскольку поле, приложенное вдоль оси z , оставляет их ориентированными случайным образом.) Энергия каждого зеемановского уровня равна $E_{M_{J}}=-M_{J}g_{J}\mu _{\mathrm {B} }H$ . нескольких К При температурах выше $M_{J}g_{J}\mu _{\mathrm {B} }H/k_{\mathrm {B} }T\ll 1$ , и мы можем применить приближение $e^{M_{J}g_{J}\mu _{\mathrm {B} }H/k_{\mathrm {B} }T\;}\simeq 1+M_{J}g_{J}\mu _{\mathrm {B} }H/k_{\mathrm {B} }T\;$ : ${\bar {m}}={\frac {\sum \limits _{M_{J}=-J}^{J}{M_{J}g_{J}\mu _{\mathrm {B} }e^{M_{J}g_{J}\mu _{\mathrm {B} }H/k_{\mathrm {B} }T\;}}}{\sum \limits _{M_{J}=-J}^{J}e^{M_{J}g_{J}\mu _{\mathrm {B} }H/k_{\mathrm {B} }T\;}}}\simeq g_{J}\mu _{\mathrm {B} }{\frac {\sum \limits _{M_{J}=-J}^{J}M_{J}\left(1+M_{J}g_{J}\mu _{\mathrm {B} }H/k_{\mathrm {B} }T\;\right)}{\sum \limits _{M_{J}=-J}^{J}\left(1+M_{J}g_{J}\mu _{\mathrm {B} }H/k_{\mathrm {B} }T\;\right)}}={\frac {g_{J}^{2}\mu _{\mathrm {B} }^{2}H}{k_{\mathrm {B} }T}}{\frac {\sum \limits _{-J}^{J}M_{J}^{2}}{\sum \limits _{M_{J}=-J}^{J}{(1)}}},$ что дает: ${\bar {m}}={\frac {g_{J}^{2}\mu _{\mathrm {B} }^{2}H}{3k_{\mathrm {B} }T}}J(J+1).$ Тогда объемная намагниченность равна $M=n{\bar {m}}={\frac {n}{3k_{\mathrm {B} }T}}\left[g_{J}^{2}J(J+1)\mu _{\mathrm {B} }^{2}\right]H,$ а восприимчивость определяется выражением $\chi ={\frac {\partial M_{\rm {m}}}{\partial H}}={\frac {n}{3k_{\rm {B}}T}}\mu _{\mathrm {eff} }^{2}{\text{ ; and }}\mu _{\mathrm {eff} }=g_{J}{\sqrt {J(J+1)}}\mu _{\mathrm {B} }.$

Когда вклады орбитального углового момента в магнитный момент малы, как это происходит для большинства органических радикалов или для октаэдрических комплексов переходных металлов с d ³ или высокоспиновый d ⁵ конфигурациях эффективный магнитный момент принимает вид (с g-фактором g _e = 2,0023... ≈ 2), $\mu _{\mathrm {eff} }\simeq 2{\sqrt {S(S+1)}}\mu _{\mathrm {B} }={\sqrt {N_{\rm {u}}(N_{\rm {u}}+2)}}\mu _{\mathrm {B} },$ где N _u — число неспаренных электронов . В случае других комплексов переходных металлов это дает полезную, хотя и несколько более грубую оценку.

Когда константа Кюри равна нулю, эффекты второго порядка, которые связывают основное состояние с возбужденными состояниями, также могут привести к парамагнитной восприимчивости, независимой от температуры, известной как восприимчивость Ван Флека .

Парамагнетизм Паули [ править ]

Для некоторых щелочных и благородных металлов электроны проводимости слабо взаимодействуют и делокализуются в пространстве, образуя ферми-газ . Для этих материалов один вклад в магнитный отклик вносит взаимодействие между спинами электронов и магнитным полем, известное как парамагнетизм Паули. Для небольшого магнитного поля $\mathbf {H}$ , дополнительная энергия на электрон от взаимодействия спина электрона с магнитным полем определяется выражением:

\Delta E=-\mu _{0}\mathbf {H} \cdot {\boldsymbol {\mu }}_{e}=-\mu _{0}\mathbf {H} \cdot \left(-g_{e}{\frac {\mu _{\mathrm {B} }}{\hbar }}\mathbf {S} \right)=\pm \mu _{0}\mu _{\mathrm {B} }H,

где $\mu _{0}$ проницаемость вакуумная , ${\boldsymbol {\mu }}_{e}$ — магнитный момент электрона , $\mu _{\rm {B}}$ – магнетон Бора , $\hbar$ - приведенная постоянная Планка, а g-фактор сокращается со спином $\mathbf {S} =\pm \hbar /2$ . $\pm$ указывает на то, что знак положительный (отрицательный), когда составляющая спина электрона в направлении $\mathbf {H}$ параллельно (антипараллельно) магнитному полю.

Для низких температур относительно температуры Ферми $T_{\rm {F}}$ (около 10 ⁴ Кельвины для металлов), плотность электронов $n_{\uparrow }$ ( $n_{\downarrow }$ ), направленные параллельно (антипараллельно) магнитному полю, можно записать как:

n_{\uparrow }\approx {\frac {n_{e}}{2}}-{\frac {\mu _{0}\mu _{\mathrm {B} }}{2}}g(E_{\mathrm {F} })H\quad ;\quad \left(n_{\downarrow }\approx {\frac {n_{e}}{2}}+{\frac {\mu _{0}\mu _{\mathrm {B} }}{2}}g(E_{\mathrm {F} })H\right),

с $n_{e}$ полная плотность свободных электронов и $g(E_{\mathrm {F} })$ электронная плотность состояний (количество состояний на энергию в объеме) при энергии Ферми $E_{\mathrm {F} }$ .

В этом приближении намагниченность определяется как произведение магнитного момента одного электрона на разницу плотностей:

M=\mu _{\mathrm {B} }(n_{\downarrow }-n_{\uparrow })=\mu _{0}\mu _{\mathrm {B} }^{2}g(E_{\mathrm {F} })H,

что дает положительную парамагнитную восприимчивость, не зависящую от температуры:

\chi _{\mathrm {P} }=\mu _{0}\mu _{\mathrm {B} }^{2}g(E_{\mathrm {F} }).

Парамагнитная восприимчивость Паули представляет собой макроскопический эффект, и его следует противопоставить диамагнитной восприимчивости Ландау , которая равна минус одной трети восприимчивости Паули и также исходит от делокализованных электронов. Восприимчивость Паули возникает из-за взаимодействия спина с магнитным полем, тогда как восприимчивость Ландау возникает из-за пространственного движения электронов и не зависит от спина. В легированных полупроводниках соотношение восприимчивостей Ландау и Паули меняется с увеличением эффективной массы носителей заряда. $m^{*}$ может отличаться от массы электрона $m_{e}$ .

Магнитный отклик, рассчитанный для газа электронов, не дает полной картины, поскольку необходимо учитывать магнитную восприимчивость, исходящую от ионов. Кроме того, эти формулы могут не работать для ограниченных систем, которые отличаются от объемных, таких как квантовые точки , или для сильных полей, как показано в эффекте Де Хааса-Ван Альфена .

Парамагнетизм Паули назван в честь физика Вольфганга Паули . До появления теории Паули отсутствие сильного парамагнетизма Кюри в металлах было открытой проблемой, поскольку ведущая модель Друде не могла объяснить этот вклад без использования квантовой статистики .Парамагнетизм Паули и диамагнетизм Ландау, по сути, являются приложениями спина и модели свободных электронов , первая из которых связана с собственным спином электронов; второе связано с их орбитальным движением. ^[5]^[6]

Примеры парамагнетиков [ править ]

Материалы, называемые «парамагнетиками», чаще всего представляют собой те, которые проявляют, по крайней мере, в заметном диапазоне температур, магнитную восприимчивость, соответствующую законам Кюри или Кюри-Вейсса. В принципе любую систему, содержащую атомы, ионы или молекулы с неспаренными спинами, можно назвать парамагнетиком, но необходимо тщательно учитывать взаимодействия между ними.

Системы с минимальным взаимодействием [ править ]

Самым узким определением было бы следующее: система с непарными спинами, не взаимодействующими друг с другом. В этом самом узком смысле единственный чистый парамагнетик представляет собой разбавленный газ из одноатомных атомов водорода . Каждый атом имеет один невзаимодействующий неспаренный электрон.

Газ атомов лития уже имеет два спаренных остовных электрона, которые вызывают диамагнитный отклик противоположного знака. Строго говоря, Li представляет собой смешанную систему, хотя, по общему признанию, диамагнитная составляющая слаба и ею часто пренебрегают. В случае более тяжелых элементов диамагнитный вклад становится более важным, а в случае металлического золота он доминирует в свойствах. Элемент водород практически никогда не называют «парамагнитным», поскольку одноатомный газ стабилен только при чрезвычайно высокой температуре; Атомы H объединяются, образуя молекулярный H2 _, и при этом магнитные моменты теряются ( гасятся ) из-за пары спинов. Следовательно, водород диамагнитен , и то же самое справедливо и для многих других элементов. Хотя электронная конфигурация отдельных атомов (и ионов) большинства элементов содержит неспаренные спины, они не обязательно являются парамагнитными, поскольку при температуре окружающей среды тушение является скорее правилом, чем исключением. Тенденция к тушению наиболее слаба для f-электронов, поскольку f (особенно 4 f ) орбитали радиально сужены и лишь слабо перекрываются с орбиталями соседних атомов. Следовательно, элементы лантаноидов с неполностью заполненными 4f-орбиталями являются парамагнитными или магнитоупорядоченными. ^[7]

Значения μ _eff для типичных d ³ и д ⁵ комплексы переходных металлов. ^[8]
Материал	μ _эфф /μ _B
[Cr(NH ₃ ) ₆ ]Br ₃	3.77
К ₃ [Cr(CN) ₆ ]	3.87
К ₃ [МоСl ₆ ]	3.79
К ₄ [В(CN) ₆ ]	3.78
[Mn(NH ₃ ) ₆ ]Cl ₂	5.92
(NH ₄ ) ₂ [Mn(SO ₄ ) ₂ ]·6H ₂ O	5.92
NH ₄ [Fe(SO ₄ ) ₂ ]·12H ₂ O	5.89

Таким образом, парамагнетики с конденсированной фазой возможны только в том случае, если взаимодействия спинов, приводящие либо к тушению, либо к упорядочению, сдерживаются структурной изоляцией магнитных центров. Это справедливо для двух классов материалов:

Молекулярные материалы с (изолированным) парамагнитным центром.
- Хорошими примерами являются координационные комплексы d- или f-металлов или белков с такими центрами, например миоглобин . В таких материалах органическая часть молекулы действует как оболочка, защищающая спины от соседей.
- Маленькие молекулы могут быть стабильными в радикальной форме, кислород O ₂ хорошим примером является . Такие системы довольно редки, поскольку они имеют тенденцию быть довольно реактивными.
Разбавленные системы.
- Растворение парамагнитных частиц в диамагнитной решетке при малых концентрациях, например Nd. ³⁺ в CaCl ₂ будет разделять ионы неодима на достаточно большие расстояния, чтобы они не взаимодействовали. Такие системы имеют первостепенное значение для того, что можно считать наиболее чувствительным методом изучения парамагнитных систем: ЭПР .

Системы с взаимодействиями [ править ]

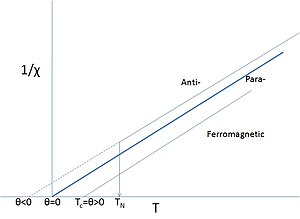
Идеализированное поведение Кюри – Вейсса; NB T _C =θ, но T _N не является θ. Парамагнитные режимы обозначены сплошными линиями. Вблизи T _N или T _C поведение обычно отклоняется от идеального.

Как говорилось выше, многие материалы, содержащие d- или f-элементы, сохраняют негашеные спины. Соли таких элементов часто проявляют парамагнитное поведение, но при достаточно низких температурах магнитные моменты могут упорядочиваться. Такие материалы нередко называют «парамагнетиками», имея в виду их парамагнитное поведение выше точек Кюри или Нееля, особенно если такие температуры очень низкие или никогда не измерялись должным образом. Даже в отношении железа нередко можно сказать, что железо становится парамагнетиком выше своей относительно высокой точки Кюри. В этом случае точка Кюри рассматривается как фазовый переход между ферромагнетиком и «парамагнетиком». Слово «парамагнетик» теперь просто относится к линейному отклику системы на приложенное поле, температурная зависимость которого требует исправленной версии закона Кюри, известного как закон Кюри-Вейсса :

\mathbf {M} ={\frac {C}{T-\theta }}\mathbf {H}

Этот измененный закон включает член θ, который описывает обменное взаимодействие, которое присутствует, хотя и преодолевается тепловым движением. Знак θ зависит от того, преобладают ли ферро- или антиферромагнитные взаимодействия, и он редко бывает точно нулевым, за исключением упомянутых выше разбавленных изолированных случаев.

Очевидно, что парамагнитное описание Кюри–Вейсса выше T _N или T _C представляет собой несколько иную интерпретацию слова «парамагнетик», поскольку оно не подразумевает отсутствие взаимодействий, а, скорее, то, что магнитная структура является случайной в отсутствие внешнего поля. при этих достаточно высоких температурах. Даже если θ близко к нулю, это не означает отсутствия взаимодействий, а лишь то, что ориентирующие ферро- и антиориентирующие антиферромагнитные взаимодействия компенсируются. Дополнительная сложность заключается в том, что взаимодействия часто различны в разных направлениях кристаллической решетки ( анизотропия ), что приводит к сложным магнитным структурам , когда-то упорядоченным.

Случайность структуры также применима ко многим металлам, которые демонстрируют чистый парамагнитный отклик в широком диапазоне температур. Однако они не подчиняются закону типа Кюри в зависимости от температуры; часто они более или менее независимы от температуры. Этот тип поведения носит странствующий характер и лучше называется парамагнетизмом Паули, но нередко можно увидеть, например, металлический алюминий, называемый «парамагнетиком», даже несмотря на то, что взаимодействия достаточно сильны, чтобы придать этому элементу очень хорошую электропроводность. .

Суперпарамагнетики [ править ]

Некоторые материалы демонстрируют индуцированное магнитное поведение, которое соответствует закону типа Кюри, но с исключительно большими значениями констант Кюри. Эти материалы известны как суперпарамагнетики . Для них характерен сильный ферромагнитный или ферримагнитный тип связи с доменами ограниченного размера, ведущими себя независимо друг от друга. По объемным свойствам такая система напоминает парамагнетик, но на микроскопическом уровне они упорядочены. Материалы действительно демонстрируют температуру упорядочения, выше которой поведение возвращается к обычному парамагнетизму (с взаимодействием). Хорошим примером являются феррожидкости , но это явление может происходить и внутри твердых тел, например, когда разбавленные парамагнитные центры вводятся в сильную коллективизированную среду ферромагнитной связи, например, когда Fe заменяется на TlCu ₂ Se ₂ или сплав AuFe. Такие системы содержат ферромагнитно связанные кластеры, которые вымерзают при более низких температурах. Их еще называют миктомагнетиками .

См. также [ править ]

Магнитохимия

Ссылки [ править ]

^ Мисслер, Г.Л. и Тарр, Д.А. (2010) Неорганическая химия , 3-е изд., Издательство Pearson/Prentice Hall, ISBN 0-13-035471-6 .
^ Парамагнетизм . Британская энциклопедия
^ «Магнитные свойства» . Химия LibreTexts . 02.10.2013 . Проверено 21 января 2020 г.
^ Нейв, Карл Л. «Магнитные свойства твердых тел» . Гиперфизика . Проверено 9 ноября 2008 г.
^ Паули, Z.Phys. 41, 81, 1927 г.
^ Ландау, Z.Phys. 64, 629, 1930 г.
^ Дженсен Дж. и Маккинтош Арканзас (1991). Редкоземельный магнетизм . Оксфорд: Кларендон Пресс. Архивировано из оригинала 12 декабря 2010 г. Проверено 12 июля 2009 г.
^ Орчард, AF (2003) Магнитохимия . Издательство Оксфордского университета.

Дальнейшее чтение [ править ]

Фейнмановские лекции по физике Vol. II, гл. 35: «Парамагнетизм и магнитный резонанс».
Чарльз Киттель, Введение в физику твердого тела (Wiley: Нью-Йорк, 1996).
Джон Дэвид Джексон, Классическая электродинамика (Wiley: Нью-Йорк, 1999).

Внешние ссылки [ править ]

«Магнетизм: модели и механизмы» в книге Э. Паварини, Э. Коха и У. Шольвека: Эмерджентные явления в коррелированной материи , Юлих, 2013, ISBN 978-3-89336-884-6

[1] Мисслер, Г.Л. и Тарр, Д.А. (2010) Неорганическая химия , 3-е изд., Издательство Pearson/Prentice Hall, ISBN 0-13-035471-6 .

[brit-2] Парамагнетизм . Британская энциклопедия

[3] «Магнитные свойства» . Химия LibreTexts . 02.10.2013 . Проверено 21 января 2020 г.

[magneticValues-4] Нейв, Карл Л. «Магнитные свойства твердых тел» . Гиперфизика . Проверено 9 ноября 2008 г.

[5] Паули, Z.Phys. 41, 81, 1927 г.

[6] Ландау, Z.Phys. 64, 629, 1930 г.

[7] Дженсен Дж. и Маккинтош Арканзас (1991). Редкоземельный магнетизм . Оксфорд: Кларендон Пресс. Архивировано из оригинала 12 декабря 2010 г. Проверено 12 июля 2009 г.

[8] Орчард, AF (2003) Магнитохимия . Издательство Оксфордского университета.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

v т и Магнетизм
Magnetic response	diamagnetism superdiamagnetism paramagnetism superparamagnetism Van Vleck paramagnetism
Magnetic states	altermagnetism antiferromagnetism ferrimagnetism ferromagnetism superferromagnetism ferromagnetic superconductor helimagnetism metamagnetism mictomagnetism spin glass amorphous magnetism spin ice