уровень Ферми

Не следует путать с энергией Ферми .

Заполнение электронных состояний в различных типах материалов в состоянии равновесия . Здесь высота — это энергия, а ширина — это плотность доступных состояний для определенной энергии в указанном материале. Оттенок соответствует распределению Ферми – Дирака ( черный : все состояния заполнены, белый : состояния не заполнены). В металлах и полуметаллах уровень Ферми EF _{лежит как} минимум внутри одной зоны.

В изоляторах и полупроводниках уровень Ферми находится внутри запрещенной зоны ; однако в полупроводниках зоны расположены достаточно близко к уровню Ферми, чтобы их можно было термически заселить электронами или дырками . «интрин». указывает на собственные полупроводники .

Уровень Ферми тела твердого — это термодинамическая работа , необходимая для добавления к телу одного электрона. Это термодинамическая величина, обычно обозначаемая μ или E _F. для краткости. Уровень Ферми не включает в себя работу, необходимую для удаления электрона оттуда, откуда он взялся.Точное понимание уровня Ферми — как он связан с электронной зонной структурой при определении электронных свойств; то, как оно связано с напряжением и потоком заряда в электронной схеме, важно для понимания физики твердого тела.

В зонной структуры теории , используемой в физике твердого тела для анализа энергетических уровней в твердом теле, уровень Ферми можно рассматривать как гипотетический энергетический уровень электрона, так что при термодинамическом равновесии этот энергетический уровень имел бы 50% вероятность быть занятым в любой момент времени . Положение уровня Ферми по отношению к уровням энергии зоны является решающим фактором в определении электрических свойств.Уровень Ферми не обязательно соответствует реальному энергетическому уровню (в изоляторе уровень Ферми лежит в запрещенной зоне ) и не требует существования зонной структуры.Тем не менее, уровень Ферми представляет собой точно определенную термодинамическую величину, и различия в уровне Ферми можно измерить просто с помощью вольтметра .

Измерение напряжения

Вольтметр заряд измеряет разницу уровней Ферми, деленную на электрона .

Иногда говорят, что электрические токи вызываются разницей электростатических потенциалов ( потенциал Гальвани ), но это не совсем так. В качестве контрпримера, устройства из нескольких материалов, такие как p – n-переходы, содержат внутренние разности электростатических потенциалов в равновесии, но без какого-либо сопутствующего чистого тока; если к месту соединения присоединить вольтметр, можно просто измерить ноль вольт. Очевидно, что электростатический потенциал не является единственным фактором, влияющим на течение заряда в материале: важную роль также играют отталкивание Паули , градиенты концентрации носителей, электромагнитная индукция и тепловые эффекты.

Фактически, величина, называемая напряжением , измеряемая в электронной схеме, имеет простую связь с химическим потенциалом электронов (уровнем Ферми).Когда выводы вольтметра прикреплены к двум точкам цепи, отображаемое напряжение является мерой общей работы, передаваемой при перемещении единичного заряда из одной точки в другую.Если простой провод соединить между двумя точками с разным напряжением (образуя короткое замыкание ), ток будет течь от положительного напряжения к отрицательному, преобразуя имеющуюся работу в тепло.

Уровень Ферми тела выражает работу, необходимую для присоединения к нему электрона, или, что эквивалентно, работу, полученную при удалении электрона.Следовательно, VA _в - V _B , наблюдаемая разность напряжений между двумя точками A и B электронной схеме точно связана с соответствующей разностью химических потенциалов µ _A - µ _B на уровне Ферми по формуле $$V_{\mathrm {A} }-V_{\mathrm {B} }={\frac {\mu _{\mathrm {A} }-\mu _{\mathrm {B} }}{-e}}$$где − e — заряд электрона .

Из приведенного выше обсуждения видно, что электроны будут перемещаться от тела с высоким µ (низкое напряжение) к телу с низким µ (высокое напряжение), если обеспечить простой путь.Этот поток электронов приведет к нижнего µ увеличению более высокого µ (из-за заряда или других эффектов отталкивания), а также к уменьшению .В конце концов, μ установится на одно и то же значение в обоих телах.Это приводит к важному факту, касающемуся равновесного (выключенного) состояния электронной схемы:

Электронная схема, находящаяся в термодинамическом равновесии, будет иметь постоянный уровень Ферми во всех ее соединенных частях.

Это также означает, что напряжение (измеренное вольтметром) между любыми двумя точками в состоянии равновесия будет равно нулю.Обратите внимание, что термодинамическое равновесие здесь требует, чтобы схема была внутренне подключена и не содержала никаких батарей или других источников питания, а также никаких изменений температуры.

Зонная структура твердых тел

Распределение Ферми-Дирака $f(\epsilon )$ против энергии $\epsilon$, с ц = 0,55 эВ и для различных температур в диапазоне 50 К < Т < 375 К.

В зонной теории твердых тел электроны занимают ряд зон, состоящих из собственных состояний энергии одной частицы, каждое из которых обозначено ϵ . Хотя эта картина одной частицы является приближенной, она значительно упрощает понимание поведения электронов и обычно дает правильные результаты при правильном применении.

Распределение Ферми –Дирака , $f(\epsilon )$, дает вероятность того, что (при термодинамическом равновесии ) состояние с энергией ϵ занято электроном: $$f(\epsilon )={\frac {1}{e^{(\epsilon -\mu )/k_{\mathrm {B} }T}+1}}$$

Здесь T — абсолютная температура , а k _B — постоянная Больцмана . Если на уровне Ферми есть состояние ( ϵ = μ ), то это состояние будет иметь 50%-ную вероятность быть занятым. Распределение показано на левом рисунке. Чем ближе f к 1, тем выше вероятность того, что это состояние занято. Чем ближе f к 0, тем выше вероятность того, что это состояние пусто.

Расположение μ внутри зонной структуры материала важно для определения электрического поведения материала.

• В изоляторе , вдали от любых состояний , µ находится в пределах большой запрещенной зоны способных проводить ток.
• В металле, полуметалле или вырожденном полупроводнике µ лежит внутри делокализованной зоны. Большое количество состояний вблизи μ термически активны и легко проводят ток.
• В собственном или слегка легированном полупроводнике µ находится достаточно близко к краю зоны, поэтому вблизи этого края зоны находится небольшое количество термически возбужденных носителей.

В полупроводниках и полуметаллах положением μ относительно зонной структуры обычно можно в значительной степени управлять путем легирования или стробирования. Эти элементы управления не меняют ц, который фиксируется электродами, а заставляют всю зонную структуру смещаться вверх и вниз (иногда также меняя форму зонной структуры). Дополнительную информацию об уровнях Ферми полупроводников см. (например) в Sze.

Привязка локальной зоны проводимости, внутренний химический потенциал и параметр ζ

Если символ ℰ используется для обозначения уровня энергии электрона, измеренного относительно энергии края окружающей его зоны ϵ _C , то в общем случае мы имеем ${\textstyle {\text{ℰ}}=\varepsilon -\varepsilon _{\rm {C}}.}$ Мы можем определить параметр ζ который относится к уровню Ферми относительно края зоны: $$\zeta =\mu -\epsilon _{\rm {C}}.$$Отсюда следует, что функцию распределения Ферми–Дирака можно записать в виде $$f({\mathcal {E}})={\frac {1}{e^{({\mathcal {E}}-\zeta )/k_{\mathrm {B} }T}+1}}.$$Зонная теория металлов была первоначально разработана Зоммерфельдом, начиная с 1927 года, который уделял большое внимание лежащим в ее основе термодинамике и статистической механике. Как ни странно, в некоторых контекстах величина ζ, привязанная к зоне , может называться уровнем Ферми , химическим потенциалом или электрохимическим потенциалом , что приводит к двусмысленности с глобальным уровнем Ферми. термины « зона проводимости», относящаяся к уровню Ферми или «внутренний химический потенциал» используются В этой статье для обозначения ζ .

Пример изменения края зоны проводимости EC _на зонной диаграмме GaAs/AlGaAs гетероперехода на основе транзистора с высокой подвижностью электронов .

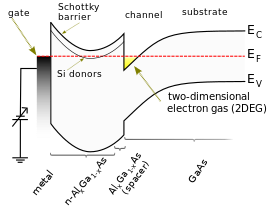
ζ напрямую связано с количеством активных носителей заряда, а также с их типичной кинетической энергией и, следовательно, напрямую участвует в определении локальных свойств материала (таких как электропроводность ). принято сосредотачиваться на значении ζ По этой причине при изучении свойств электронов в одном однородном проводящем материале .По аналогии с энергетическими состояниями свободного электрона, ℰ состояния — это кинетическая энергия этого состояния, а ϵ _C — его потенциальная энергия . Имея это в виду, параметр ζ можно также назвать кинетической энергией Ферми .

В отличие от μ , параметр ζ не является константой в равновесии, а скорее варьируется от места к месту в материале из-за изменений ϵ _C , который определяется такими факторами, как качество материала и примеси/легирующие добавки.Вблизи поверхности полупроводника или полуметалла ζ можно сильно контролировать с помощью внешних электрических полей, как это делается в полевом транзисторе . В многополосном материале ζ может даже принимать несколько значений в одном месте.Например, в куске алюминия есть две зоны проводимости, пересекающие уровень Ферми (в других материалах зон еще больше); каждая полоса имеет разную краевую энергию ϵ _C и разное ζ .

Значение ζ при нулевой температуре широко известно как энергия Ферми , иногда обозначаемая ζ ₀ . Как ни странно (опять же), название « энергия Ферми» иногда используется для обозначения ζ при ненулевой температуре.

Температура вне равновесия

См. Также: Квази-уровень Ферми.

Уровень Ферми, µ , и температура, T , являются четко определенными константами для твердотельного устройства в ситуации термодинамического равновесия, например, когда оно сидит на полке и ничего не делает. Когда устройство выведено из равновесия и введено в эксплуатацию, то, строго говоря, уровень Ферми и температура перестают быть четко определенными. К счастью, часто можно определить квазиуровень Ферми и квазитемпературу для данного места, которые точно описывают заселенность состояний с точки зрения теплового распределения. Говорят, что устройство находится в квазиравновесии тогда и там, где такое описание возможно.

Квазиравновесный подход позволяет построить простую картину некоторых неравновесных эффектов, таких как электропроводность куска металла (как результат градиента ц ) или его теплопроводность (как результат градиента Т ). Квази- ц и квази- Т могут меняться (или вообще не существовать) в любой неравновесной ситуации, например:

• Если в системе имеется химический дисбаланс (как в аккумуляторе ).
• Если система подвергается воздействию изменяющихся электромагнитных полей (как в конденсаторах , катушках индуктивности и трансформаторах ).
• При освещении источником света с другой температурой, например солнцем (как в солнечных батареях ),
• Когда температура внутри устройства непостоянна (как в термопарах ),
• Когда устройство было изменено, но не успело восстановить равновесие (как в пьезоэлектрических или пироэлектрических веществах).

В некоторых ситуациях, например, сразу после того, как материал подвергся воздействию высокоэнергетического лазерного импульса, распределение электронов невозможно описать каким-либо тепловым распределением.В этом случае невозможно определить квазиуровень Ферми или квазитемпературу; электроны просто называются нетермализованными . В менее драматичных ситуациях, например, в солнечном элементе при постоянном освещении, квазиравновесное описание может быть возможным, но требует присвоения разных значений μ и T разным зонам (зона проводимости и валентная зона). Даже в этом случае значения μ и T могут прерывисто прыгать на границе раздела материалов (например, p–n-переходе ) при прохождении тока и быть плохо определены на самой границе раздела.

Технические особенности

Проблемы с терминологией

Термин «уровень Ферми» в основном используется при обсуждении физики твердого тела электронов в полупроводниках , и точное использование этого термина необходимо для описания зонных диаграмм в устройствах, состоящих из разных материалов с разными уровнями легирования.Однако в этих контекстах можно также увидеть, что уровень Ферми используется неточно для обозначения уровня Ферми, привязанного к зоне , µ − ϵ _C , названного ζ выше .Обычно ученые и инженеры говорят о «контроле», « закреплении » или «настройке» уровня Ферми внутри проводника, тогда как на самом деле они описывают изменения ϵ _C из-за легирования или эффекта поля .Фактически, термодинамическое равновесие гарантирует, что уровень Ферми в проводнике всегда фиксирован и точно равен уровню Ферми электродов; только зонная структура (не уровень Ферми) может быть изменена легированием или эффектом поля (см. также зонную диаграмму ).Аналогичная двусмысленность существует между терминами «химический потенциал» и «электрохимический потенциал» .

Также важно отметить, что уровень Ферми не обязательно совпадает с Ферми энергией .В более широком контексте квантовой механики термин « энергия Ферми» обычно относится к максимальной кинетической энергии фермиона в идеализированном невзаимодействующем, свободном от беспорядка ферми-газе с нулевой температурой .Эта концепция очень теоретическая (невзаимодействующего ферми-газа не существует, и невозможно достичь нулевой температуры). Однако он находит некоторое применение при приблизительном описании белых карликов , нейтронных звезд , атомных ядер и электронов в металлах .С другой стороны, в области физики и техники полупроводников энергия Ферми часто используется для обозначения уровня Ферми, описанного в этой статье.

Привязка к уровню Ферми и расположение нулевого уровня Ферми

Подобно выбору начала координат в системе координат, нулевая точка энергии может быть определена произвольно. Наблюдаемые явления зависят только от разницы энергий.Однако при сравнении различных тел важно, чтобы все они были последовательны в выборе местоположения нулевой энергии, иначе будут получены бессмысленные результаты.Поэтому может быть полезно явно указать общую точку, чтобы гарантировать согласованность различных компонентов.С другой стороны, если контрольная точка по своей сути неоднозначна (например, «вакуум», см. ниже), это вызовет больше проблем.

Практичным и вполне оправданным выбором общей точки является громоздкий физический проводник, такой как электрическое заземление или земля.Можно считать, что такой проводник находится в хорошем термодинамическом равновесии, и поэтому его µ четко определен.Он обеспечивает резервуар заряда, поэтому большое количество электронов может быть добавлено или удалено без возникновения эффекта зарядки.Он также имеет то преимущество, что он доступен, так что уровень Ферми любого другого объекта можно измерить просто с помощью вольтметра.

Почему нецелесообразно использовать «энергию в вакууме» в качестве эталонного нуля

Когда два изображенных здесь металла находятся в термодинамическом равновесии, как показано (равные уровни Ферми EF ₎ , вакуумный электростатический потенциал φ не является плоским из-за разницы в работе выхода .

В принципе, можно было бы рассмотреть возможность использования состояния неподвижного электрона в вакууме в качестве точки отсчета для энергий.Этот подход нецелесообразен, если не стараться точно определить, где находится вакуум . Проблема в том, что не все точки в вакууме эквивалентны.

При термодинамическом равновесии в вакууме типично существование разности электрических потенциалов порядка 1 В ( вольта-потенциалы ).Источником этого изменения вакуумного потенциала является изменение работы выхода между различными проводящими материалами, подвергающимися воздействию вакуума.Непосредственно за пределами проводника электростатический потенциал сильно зависит от материала, а также от того, какая поверхность выбрана (ориентация кристалла, загрязнение и другие детали).

Параметром, который дает наилучшее приближение к универсальности, является предложенный выше земной уровень Ферми. Это также имеет то преимущество, что его можно измерить с помощью вольтметра.

Эффекты дискретной зарядки в небольших системах

В тех случаях, когда «эффектами зарядки» одного электрона нельзя пренебречь, приведенные выше определения следует уточнить. Например, рассмотрим конденсатор , состоящий из двух одинаковых параллельных пластин. Если конденсатор незаряжен, уровень Ферми одинаков с обеих сторон, поэтому можно подумать, что для перемещения электрона с одной пластины на другую не требуется никакой энергии. Но когда электрон переместился, конденсатор стал (слегка) заряженным, так что на это требуется небольшое количество энергии. В обычном конденсаторе это незначительно, но в наноконденсаторе это может быть более важно.

В этом случае необходимо точно определить термодинамическое определение химического потенциала, а также состояние устройства: изолировано ли оно электрически или подключено к электроду?

• Когда тело способно обмениваться электронами и энергией с электродом (резервуаром), оно описывается большим каноническим ансамблем . Можно сказать, что значение химического потенциала μ фиксируется электродом, а число электронов N на теле может колебаться. В этом случае химический потенциал тела представляет собой бесконечно малую работу, необходимую для увеличения среднего числа электронов на бесконечно малую величину (хотя число электронов в любой момент времени является целым числом, среднее число непрерывно меняется): $$\mu (\left\langle N\right\rangle ,T)=\left({\frac {\partial F}{\partial \left\langle N\right\rangle }}\right)_{T},$$ где F ( N , T ) — функция свободной энергии большого канонического ансамбля.
• Если число электронов в теле фиксировано (но тело по-прежнему термически связано с термостатом), то оно находится в каноническом ансамбле . В данном случае мы можем определить «химический потенциал» буквально как работу, необходимую для добавления одного электрона к телу, которое уже имеет ровно N электронов. $$\mu '(N,T)=F(N+1,T)-F(N,T),$$ где F ( N , T ) — функция свободной энергии канонического ансамбля, альтернативно: $$\mu ''(N,T)=F(N,T)-F(N-1,T)=\mu '(N-1,T).$$

Эти химические потенциалы не эквивалентны, μ ≠ μ ′ ≠ μ ″ , за исключением термодинамического предела . Это различие важно для небольших систем, таких как те, в которых наблюдается кулоновская блокада . Параметр μ (т. е. в случае, когда количество электронов может колебаться) остается точно связанным с напряжением вольтметра даже в небольших системах.Если быть точным, то уровень Ферми определяется не детерминированным событием зарядки одним зарядом электрона, а скорее статистическим событием зарядки бесконечно малой долей электрона.