Электрический потенциал

Электрический потенциал
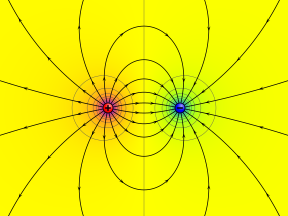
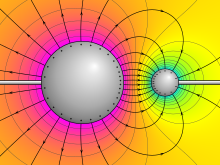Электрический потенциал
	Электрический потенциал вокруг двух противоположно заряженных проводящих сфер. Фиолетовый представляет самый высокий потенциал, желтый — ноль, а голубой — самый низкий потенциал. Линии электрического поля показаны выходящими перпендикулярно поверхности каждой сферы.
Общие символы	В , φ
И объединились	вольт
Другие подразделения	статвольт
В базовых единицах СИ	V = kg⋅m 2 ⋅s −3 ⋅A −1
Обширный ?	да
Измерение	М Л 2 Т −3 я −1

Электрический потенциал (также называемый потенциалом электрического поля , падением потенциала, электростатическим потенциалом ) определяется как количество рабочей энергии, необходимой на единицу электрического заряда для перемещения заряда из опорной точки в определенную точку электрического поля. Точнее, электрический потенциал — это энергия, приходящаяся на единицу заряда пробного заряда , который настолько мал, что возмущение рассматриваемого поля незначительно. Предполагается, что движение поперек поля происходит с пренебрежимо малым ускорением, чтобы пробный заряд не приобретал кинетическую энергию и не производил излучение. По определению электрический потенциал в контрольной точке равен нулю единиц. Обычно опорной точкой является земля или точка, находящаяся на бесконечности , хотя можно использовать любую точку.

В классической электростатике электростатическое поле представляет собой векторную величину, выражаемую как градиент электростатического потенциала, который представляет собой скалярную величину, обозначаемую $V$ или иногда $φ$ , ^[1] равна электрической потенциальной энергии любой заряженной частицы в любом месте (измеряется в джоулях ), разделенной на заряд этой частицы (измеряется в кулонах ). При делении заряда частицы получается частное, которое является свойством самого электрического поля. Короче говоря, электрический потенциал — это электрическая потенциальная энергия на единицу заряда.

Это значение может быть рассчитано либо в статическом (независимом от времени), либо в динамическом (изменяющемся во времени) электрическом поле в определенное время с единицей измерения джоулей на кулон (Дж⋅К ⁻¹) или вольт (В). Электрический потенциал на бесконечности предполагается равным нулю.

В электродинамике , когда присутствуют изменяющиеся во времени поля, электрическое поле не может быть выражено только как скалярный потенциал . Вместо этого электрическое поле может быть выражено как скалярным электрическим потенциалом, так и магнитным векторным потенциалом . ^[2] Электрический потенциал и магнитный векторный потенциал вместе образуют четырехвектор , так что два вида потенциала смешиваются при преобразованиях Лоренца .

Практически электрический потенциал является непрерывной функцией во всем пространстве, потому что пространственная производная разрывного электрического потенциала создает электрическое поле невозможно бесконечной величины. Примечательно, что электрический потенциал идеализированного точечного заряда (пропорциональный $1 ⁄ r$ , где $r —$ расстояние от точечного заряда) непрерывен во всем пространстве, кроме места расположения точечного заряда. Хотя электрическое поле не является непрерывным на идеализированном поверхностном заряде , оно не бесконечно в любой точке. Следовательно, электрический потенциал непрерывен на идеализированном поверхностном заряде. Кроме того, идеализированная линия заряда имеет электрический потенциал (пропорциональный $ln(r)$ , где $r —$ радиальное расстояние от линии заряда) и непрерывен везде, кроме линии заряда.

Введение

Классическая механика исследует такие понятия, как сила , энергия и потенциал . ^[3] Сила и потенциальная энергия напрямую связаны между собой. Суммарная сила, действующая на любой объект, заставляет его ускоряться . По мере того как объект движется в направлении действующей на него силы, его потенциальная энергия уменьшается. Например, гравитационная потенциальная энергия пушечного ядра на вершине холма больше, чем у подножия холма. Когда он катится вниз по склону, его потенциальная энергия уменьшается и преобразуется в движение – кинетическую энергию .

Можно определить потенциал определенных силовых полей так, что потенциальная энергия объекта в этом поле зависит только от положения объекта относительно поля. Двумя такими силовыми полями являются гравитационное поле и электрическое поле (при отсутствии изменяющихся во времени магнитных полей). Такие поля влияют на объекты из-за внутренних свойств (например, массы или заряда) и положения объектов.

Объект может обладать свойством, известным как электрический заряд . Поскольку электрическое поле оказывает силу на заряженный объект, если объект имеет положительный заряд, сила будет направлена в направлении вектора электрического поля в месте расположения заряда; если заряд отрицательный, сила будет направлена в противоположном направлении.

Величина силы определяется количеством заряда, умноженным на величину вектора электрического поля:

$|\mathbf {F} |=q|\mathbf {E} |.$

Электростатика

Электрический потенциал отдельных положительных и отрицательных точечных зарядов показан в диапазоне цветов от пурпурного (+), желтого (0) до голубого (-). Круговые контуры представляют собой эквипотенциальные линии. Линии электрического поля покидают положительный заряд и входят в отрицательный заряд.

Электрический потенциал вблизи двух противоположных точечных зарядов.

Электрический потенциал в точке $r$ в статическом электрическом поле $E$ определяется линейным интегралом

$V_{\mathbf {E} }=-\int _{\mathcal {C}}\mathbf {E} \cdot \mathrm {d} {\boldsymbol {\ell }}\,$

где $C$ — произвольный путь от некоторой фиксированной точки отсчета до $r$ ; он определяется однозначно с точностью до константы, которая прибавляется или вычитается из интеграла. В электростатике уравнение Максвелла-Фарадея показывает, что ротор ${\textstyle \nabla \times \mathbf {E} }$ равно нулю, что делает электрическое поле консервативным . Таким образом, приведенный выше линейный интеграл не зависит от конкретного выбранного пути $C$ , а только от его конечных точек, что делает ${\textstyle V_{\mathbf {E} }}$ четко выражены везде. Тогда градиентная теорема позволяет нам написать:

$\mathbf {E} =-\mathbf {\nabla } V_{\mathbf {E} }\,$

Это означает, что электрическое поле направлено «вниз» в сторону более низких напряжений. По закону Гаусса можно также найти потенциал, удовлетворяющий уравнению Пуассона : $\mathbf {\nabla } \cdot \mathbf {E} =\mathbf {\nabla } \cdot \left(-\mathbf {\nabla } V_{\mathbf {E} }\right)=-\nabla ^{2}V_{\mathbf {E} }=\rho /\varepsilon _{0}$

где $ρ$ — полная плотность заряда и ${\textstyle \mathbf {\nabla } \cdot }$ обозначает расхождение .

Понятие электрического потенциала тесно связано с потенциальной энергией . Пробный заряд q $,$ имеет электрическую потенциальную энергию U $E определяемую$ выражением

$U_{\mathbf {E} }=q\,V.$

Потенциальная энергия, а следовательно, и электрический потенциал, определяются только с точностью до аддитивной константы: нужно произвольно выбрать положение, в котором потенциальная энергия и электрический потенциал равны нулю.

Эти уравнения нельзя использовать, если ${\textstyle \nabla \times \mathbf {E} \neq \mathbf {0} }$ , т. е. в случае неконсервативного электрического поля (вызванного изменяющимся магнитным полем ; см. уравнения Максвелла ). Обобщение электрического потенциала на этот случай описано в разделе § Обобщение на электродинамику .

Электрический потенциал из-за точечного заряда

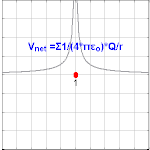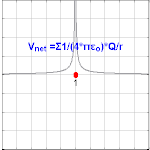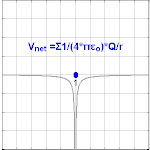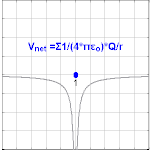
Электрический потенциал, возникающий из-за точечного заряда $Q$ на расстоянии $r$ от места расположения $Q$ , равен $V_{\mathbf {E} }={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q}{r}},$ где $ε 0$ — ^[4], $V E$ известен как кулоновский потенциал . Обратите внимание, что, в отличие от величины электрического поля, создаваемого точечным зарядом, электрический потенциал масштабируется пропорционально обратной величине радиуса, а не квадрату радиуса.

Электрический потенциал в любом месте $r$ в системе точечных зарядов равен сумме отдельных электрических потенциалов каждого точечного заряда в системе. Этот факт существенно упрощает расчеты, поскольку сложение потенциальных (скалярных) полей существенно проще, чем сложение электрических (векторных) полей. В частности, потенциал набора дискретных точечных зарядов $q i$ в точках $r i$ становится

$V_{\mathbf {E} }(\mathbf {r} )={\frac {1}{4\pi \varepsilon _{0}}}\sum _{i=1}^{n}{\frac {q_{i}}{|\mathbf {r} -\mathbf {r} _{i}|}}\,$

где

$r$ – точка, в которой оценивается потенциал;
$r i$ — точка, в которой имеется ненулевой заряд; и
$q i$ — заряд в точке $r i$ .

И потенциал непрерывного распределения заряда $ρ (r)$ становится

$V_{\mathbf {E} }(\mathbf {r} )={\frac {1}{4\pi \varepsilon _{0}}}\int _{R}{\frac {\rho (\mathbf {r} ')}{|\mathbf {r} -\mathbf {r} '|}}\mathrm {d} ^{3}r'\,,$

где

$r$ – точка, в которой оценивается потенциал;
$R$ — область, содержащая все точки, в которых плотность заряда отлична от нуля;
$r'$ — точка внутри $R$ ; и
$ρ (r ’)$ — плотность заряда в точке $r ’$ .

Приведенные выше уравнения для электрического потенциала (и все используемые здесь уравнения) имеют форму, необходимую для единиц СИ . В некоторых других (менее распространенных) системах единиц, таких как CGS-Gaussian , многие из этих уравнений будут изменены.

Обобщение на электродинамику

Когда присутствуют изменяющиеся во времени магнитные поля (что верно всякий раз, когда существуют изменяющиеся во времени электрические поля и наоборот), невозможно описать электрическое поле просто как скалярный потенциал $V,$ поскольку электрическое поле больше не является консервативным : $\textstyle \int _{C}\mathbf {E} \cdot \mathrm {d} {\boldsymbol {\ell }}$ зависит от пути, потому что $\mathbf {\nabla } \times \mathbf {E} \neq \mathbf {0}$ (из-за уравнения Максвелла-Фарадея ).

Вместо этого все еще можно определить скалярный потенциал, включив также магнитный векторный потенциал $A$ . В частности, $A$ определяется так, чтобы удовлетворять:

$\mathbf {B} =\mathbf {\nabla } \times \mathbf {A}$

где $B$ — магнитное поле . По основной теореме векторного исчисления такую $А$ всегда можно найти, поскольку дивергенция магнитного поля всегда равна нулю из-за отсутствия магнитных монополей . Теперь количество $\mathbf {F} =\mathbf {E} +{\frac {\partial \mathbf {A} }{\partial t}}$ является консервативным полем, поскольку ротор $\mathbf {E}$ отменяется поворотом ${\frac {\partial \mathbf {A} }{\partial t}}$ по уравнению Максвелла-Фарадея . Поэтому можно написать $\mathbf {E} =-\mathbf {\nabla } V-{\frac {\partial \mathbf {A} }{\partial t}},$

где $V$ определяемый консервативным полем $F.$ — скалярный потенциал ,

Электростатический потенциал — это просто частный случай этого определения, где $A$ не зависит от времени. С другой стороны, для полей, изменяющихся во времени, $-\int _{a}^{b}\mathbf {E} \cdot \mathrm {d} {\boldsymbol {\ell }}\neq V_{(b)}-V_{(a)}$ в отличие от электростатики.

Свобода измерения

К электростатическому потенциалу можно добавить любую константу, не влияя на электрическое поле. В электродинамике электрический потенциал имеет бесконечно много степеней свободы. Для любого (возможно, меняющегося во времени или пространстве) скалярного поля $𝜓$ мы можем выполнить следующее калибровочное преобразование , чтобы найти новый набор потенциалов, которые создают одни и те же электрические и магнитные поля: ^[5]

${\begin{aligned}V^{\prime }&=V-{\frac {\partial \psi }{\partial t}}\\\mathbf {A} ^{\prime }&=\mathbf {A} +\nabla \psi \end{aligned}}$

При различных вариантах измерения электрический потенциал может иметь совершенно разные свойства. В кулоновской калибровке электрический потенциал определяется уравнением Пуассона

$\nabla ^{2}V=-{\frac {\rho }{\varepsilon _{0}}}$

как и в электростатике. Однако в калибровке Лоренца электрический потенциал представляет собой запаздывающий потенциал , распространяющийся со скоростью света и являющийся решением неоднородного волнового уравнения :

$\nabla ^{2}V-{\frac {1}{c^{2}}}{\frac {\partial ^{2}V}{\partial t^{2}}}=-{\frac {\rho }{\varepsilon _{0}}}$

Единицы

является Производной единицей электрического потенциала в системе СИ вольт ( в честь Алессандро Вольты ), обозначаемый как V, поэтому разность электрических потенциалов между двумя точками в пространстве известна как напряжение . Старые агрегаты сегодня используются редко. Варианты системы единиц сантиметр-грамм-секунда включали ряд различных единиц электрического потенциала, в том числе абвольт и статвольт .

Потенциал Гальвани в сравнении с электрохимическим потенциалом

Внутри металлов (а также других твердых тел и жидкостей) на энергию электрона влияет не только электрический потенциал, но и конкретная атомная среда, в которой он находится. Когда вольтметр подключают между двумя разными типами металлов, он измеряет , разность потенциалов скорректированная для различных атомных сред. ^[6] Величина, измеряемая вольтметром, называется электрохимическим потенциалом или уровнем Ферми , а чистый нескорректированный электрический потенциал $V$ иногда называют Гальвани потенциалом $φ$ . Термины «напряжение» и «электрический потенциал» немного двусмысленны, но к любому из них можно относиться в разных контекстах.

Общие формулы


Конфигурация зарядки	Электрический потенциал
Бесконечный провод	$V=-{\frac {\lambda }{2\pi \varepsilon _{0}}}\ln x,$ где $\lambda$ — однородная линейная плотность заряда.
Бесконечно большая поверхность	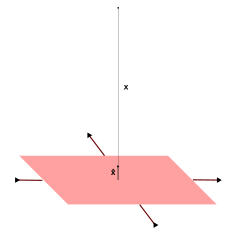$V=-{\frac {\sigma x}{2\varepsilon _{0}}},$ где $\sigma$ — однородная поверхностная плотность заряда.
Бесконечно длинный цилиндрический объем	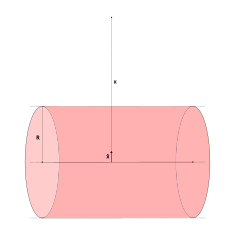$V=-{\frac {\lambda }{2\pi \varepsilon _{0}}}\ln x,$ где $\lambda$ — однородная линейная плотность заряда.
Сферический объем	$V={\frac {Q}{4\pi \varepsilon _{0}x}},$ вне сферы, где $Q$ – полный заряд, равномерно распределенный в объеме.	$V={\frac {Q(3R^{2}-r^{2})}{8\pi \varepsilon _{0}R^{3}}},$ внутри сферы, где $Q$ – полный заряд, равномерно распределенный в объеме.
Сферическая поверхность	$V={\frac {Q}{4\pi \varepsilon _{0}x}},$ вне сферы, где $Q$ – полный заряд, равномерно распределенный по поверхности.	$V={\frac {Q}{4\pi \varepsilon _{0}R}},$ внутри сферы для равномерного распределения заряда.
Заряженное кольцо	$V={\frac {Q}{4\pi \varepsilon _{0}{\sqrt {R^{2}+x^{2}}}}},$ на оси, где $Q$ – полный заряд, равномерно распределенный по кольцу.
Заряженный диск	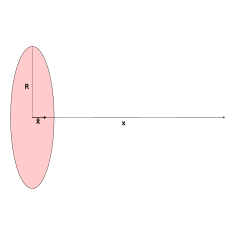$V={\frac {\sigma }{2\varepsilon _{0}}}\left[{\sqrt {x^{2}+R^{2}}}-x\right],$ на оси, где $\sigma$ – однородная поверхностная плотность заряда.
Электрический диполь	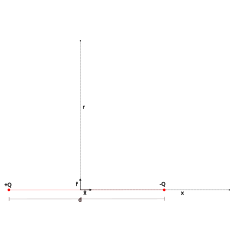$V=0,$ в экваториальной плоскости.	$V={\frac {p}{4\pi \varepsilon _{0}x^{2}}},$ на оси (при том, что $x\gg d$ ), где $x$ также может быть отрицательным, чтобы указать положение в противоположном направлении оси, и $p$ – величина электрического дипольного момента .

См. также

Ссылки

^ Гольдштейн, Герберт (июнь 1959 г.). Классическая механика . США: Аддисон-Уэсли. п. 383. ИСБН 0201025108 .
^ Гриффитс, Дэвид Дж. (1999). Введение в электродинамику . Пирсон Прентис Холл. стр. 416–417. ISBN 978-81-203-1601-0 .
^ Янг, Хью А.; Фридман, Роджер Д. (2012). Университетская физика Сирса и Земанского с современной физикой (13-е изд.). Бостон: Аддисон-Уэсли. п. 754.
^ «Значение CODATA 2022: электрическая проницаемость вакуума» . Справочник NIST по константам, единицам измерения и неопределенности . НИСТ . Май 2024 года . Проверено 18 мая 2024 г.
^ Гриффитс, Дэвид Дж. (1999). Введение в электродинамику (3-е изд.). Прентис Холл. п. 420. ИСБН 013805326X .
^ Багоцкий В.С. (2006). Основы электрохимии . Джон Уайли и сыновья. п. 22. ISBN 978-0-471-70058-6 .

Дальнейшее чтение

Политцер П., Трулар Д.Г. (1981). Химические применения атомных и молекулярных электростатических потенциалов: реакционная способность, структура, рассеяние и энергетика органических, неорганических и биологических систем . Бостон, Массачусетс: Springer US. ISBN 978-1-4757-9634-6 .
Сен К., Мюррей Дж.С. (1996). Молекулярные электростатические потенциалы: концепции и приложения . Амстердам: Эльзевир. ISBN 978-0-444-82353-3 .
Гриффитс-ди-джей (1999). Введение в электродинамику (3-е изд.). Прентис Холл. ISBN 0-13-805326-Х .
Джексон Джей Ди (1999). Классическая электродинамика (3-е изд.). John Wiley & Sons, Inc. США: ISBN 978-0-471-30932-1 .
Вангнесс РК (1986). Электромагнитные поля (2-е, исправленное, иллюстрированное изд.). Уайли. ISBN 978-0-471-81186-2 .

[1] Гольдштейн, Герберт (июнь 1959 г.). Классическая механика . США: Аддисон-Уэсли. п. 383. ИСБН 0201025108 .

[2] Гриффитс, Дэвид Дж. (1999). Введение в электродинамику . Пирсон Прентис Холл. стр. 416–417. ISBN 978-81-203-1601-0 .

[3] Янг, Хью А.; Фридман, Роджер Д. (2012). Университетская физика Сирса и Земанского с современной физикой (13-е изд.). Бостон: Аддисон-Уэсли. п. 754.

[physconst-eps0-4] «Значение CODATA 2022: электрическая проницаемость вакуума» . Справочник NIST по константам, единицам измерения и неопределенности . НИСТ . Май 2024 года . Проверено 18 мая 2024 г.

[5] Гриффитс, Дэвид Дж. (1999). Введение в электродинамику (3-е изд.). Прентис Холл. п. 420. ИСБН 013805326X .

[6] Багоцкий В.С. (2006). Основы электрохимии . Джон Уайли и сыновья. п. 22. ISBN 978-0-471-70058-6 .

[1]

[2]

[3]

[4]

[5]

[6]