Емкость

О емкости кровеносных сосудов см. Податливость (физиология) .

Общие символы	С
И объединились	лошадь
Другие подразделения	мкФ, нФ, пФ
В базовых единицах СИ	Ф = А 2 с 4 кг −1 м −2
Выводы из другие количества	C = заряд / напряжение
Измерение	${\mathsf {L}}^{-2}{\mathsf {M}}^{-1}{\mathsf {T}}^{4}{\mathsf {I}}^{2}$

Емкость — это способность материального объекта или устройства хранить электрический заряд . Он измеряется зарядом в ответ на разницу электрических потенциалов , выраженную как отношение этих величин. Общепризнанными являются два тесно связанных понятия емкости: собственная емкость и взаимная емкость . Объект, который может быть электрически заряжен, обладает собственной емкостью, для которой измеряется электрический потенциал между объектом и землей. Взаимная емкость измеряется между двумя компонентами и особенно важна при работе конденсатора — элементарного линейного электронного компонента , предназначенного для добавления емкости в электрическую цепь .

Емкость между двумя проводниками зависит только от геометрии; площадь противоположной поверхности проводников и расстояние между ними, а также диэлектрическая проницаемость любого диэлектрического материала между ними. Для многих диэлектрических материалов диэлектрическая проницаемость и, следовательно, емкость не зависят от разности потенциалов между проводниками и общего заряда на них.

Единицей в системе СИ емкости является фарад (обозначение: F), названный в честь английского физика Майкла Фарадея . Конденсатор емкостью 1 фарад, заряженный электрическим зарядом в 1 кулон , имеет разность потенциалов в 1 вольт . между его обкладками Обратная величина емкости называется эластичностью .

Собственная емкость

При обсуждении электрических цепей термин «емкость» обычно является сокращением взаимной емкости между двумя соседними проводниками, например двумя обкладками конденсатора. Однако каждый изолированный проводник также обладает емкостью, называемой здесь собственной емкостью . Он измеряется количеством электрического заряда, который необходимо добавить к изолированному проводнику, чтобы повысить его электрический потенциал на одну единицу измерения, например, на один вольт . Точкой отсчета для этого потенциала является теоретическая полая проводящая сфера бесконечного радиуса с проводником, расположенным внутри этой сферы.

Собственная емкость проводника определяется соотношением заряда и электрического потенциала:

$$C={\frac {q}{V}},$$

где

• ${\textstyle q}$ удержано ли обвинение,
• ${\textstyle V={\frac {1}{4\pi \varepsilon _{0}}}\int {\frac {\sigma }{r}}\,dS}$ электрический потенциал,
• ${\textstyle \sigma }$ - поверхностная плотность заряда,
• ${\textstyle dS}$ — бесконечно малый элемент площади на поверхности проводника,
• ${\textstyle r}$ длина от ${\textstyle dS}$ к неподвижной точке М на проводнике,
• $\varepsilon _{0}$ - диэлектрическая проницаемость вакуума .

Используя этот метод, собственная емкость проводящей сферы радиуса ${\textstyle R}$ в свободном пространстве (т.е. вдали от любых других распределений заряда):

$$C=4\pi \varepsilon _{0}R.$$

Примеры значений собственной емкости:

• для верхней «тарелки» генератора Ван де Граафа , обычно сферы радиусом 20 см: 22,24 пФ,
• планета Земля : около 710 мкФ.

Межобмоточную емкость катушки иногда называют собственной емкостью. но это другое явление. На самом деле это взаимная емкость между отдельными витками катушки, которая представляет собой разновидность паразитной емкости . Эта собственная емкость является важным фактором на высоких частотах: она изменяет полное сопротивление катушки и вызывает параллельный резонанс . Во многих приложениях это нежелательный эффект, устанавливающий верхний предел частоты для правильной работы схемы.

Взаимная емкость

Распространенной формой является конденсатор с параллельными пластинами , который состоит из двух проводящих пластин, изолированных друг от друга, обычно между диэлектрическим материалом. В конденсаторе с параллельными пластинами емкость почти пропорциональна площади поверхности проводящих пластин и обратно пропорциональна расстоянию между пластинами.

Если заряды на пластинах ${\textstyle +q}$ и ${\textstyle -q}$, и ${\textstyle V}$ дает напряжение между обкладками, затем емкость ${\textstyle C}$ дается

$$C={\frac {q}{V}},$$

напряжения/ тока что дает соотношение

$$i(t)=C{\frac {dv(t)}{dt}}+V{\frac {dC}{dt}},$$

где ${\textstyle {\frac {dv(t)}{dt}}}$ - мгновенная скорость изменения напряжения, а ${\textstyle {\frac {dC}{dt}}}$ – мгновенная скорость изменения емкости. Для большинства приложений изменение емкости с течением времени незначительно, поэтому вы можете уменьшить ее до:

$$i(t)=C{\frac {dv(t)}{dt}},$$

Энергия, запасенная в конденсаторе, находится интегрированием работы ${\textstyle W}$:

$$W_{\text{charging}}={\frac {1}{2}}CV^{2}.$$

Матрица емкости

Рассмотрение выше ограничивается случаем двух проводящих пластин, хотя и произвольного размера и формы. Определение $C=Q/V$ не применяется, когда имеется более двух заряженных пластин или когда чистый заряд на двух пластинах не равен нулю. Чтобы справиться с этим случаем, Джеймс Клерк Максвелл ввел свои коэффициенты потенциала . Если три (почти идеальных) проводника имеют заряды $Q_{1},Q_{2},Q_{3}$, то напряжение на проводнике 1 определяется выражением

$$V_{1}=P_{11}Q_{1}+P_{12}Q_{2}+P_{13}Q_{3},$$

и аналогично для остальных напряжений. Герман фон Гельмгольц и сэр Уильям Томсон показали, что коэффициенты потенциала симметричны, так что $P_{12}=P_{21}$и т. д. Таким образом, систему можно описать набором коэффициентов, известных как матрица упругости или матрица обратной емкости , которая определяется как:

$$P_{ij}={\frac {\partial V_{i}}{\partial Q_{j}}}.$$

Отсюда взаимная емкость $C_{m}$ между двумя объектами можно определить решив общий заряд ${\textstyle Q}$ и используя $C_{m}=Q/V$.

$$C_{m}={\frac {1}{(P_{11}+P_{22})-(P_{12}+P_{21})}}.$$

Поскольку ни одно реальное устройство не удерживает совершенно равные и противоположные заряды на каждой из двух «обкладок», в конденсаторах сообщается взаимная емкость.

Сборник коэффициентов $C_{ij}={\frac {\partial Q_{i}}{\partial V_{j}}}$ известна как матрица емкости , и является обратной матрицей упругости.

Конденсаторы

Основная статья: Конденсатор

Емкость большинства конденсаторов, используемых в электронных схемах, обычно на несколько порядков меньше фарада . Наиболее распространенными единицами измерения емкости являются микрофарад (мкФ), нанофарад (нФ), пикофарад (пФ), а в микросхемах — фемтофарад (фФ). В некоторых приложениях также используются суперконденсаторы , размер которых может быть намного больше, вплоть до сотен фарад, а паразитные емкостные элементы могут быть меньше фемтофарад. В исторических текстах используются другие, устаревшие дробные фарада, такие как «mf» и «mfd» для микрофарад (мкФ); «ммф», «ммфд», «п.п.м.», «мкФ» для пикофарадов (пФ).

Емкость можно рассчитать, если известны геометрия проводников и диэлектрические свойства изолятора между проводниками. Емкость пропорциональна площади перекрытия и обратно пропорциональна расстоянию между проводящими листами. Чем ближе листы расположены друг к другу, тем больше емкость.

Примером может служить емкость конденсатора, состоящего из двух параллельных пластин площадью ${\textstyle A}$ разделенные расстоянием ${\textstyle d}$. Если ${\textstyle d}$ достаточно мала по отношению к наименьшей хорде ${\textstyle A}$, с высокой степенью точности выполняется:

$$\ C=\varepsilon {\frac {A}{d}};$$

$$\varepsilon =\varepsilon _{0}\varepsilon _{r},$$

где

• ${\textstyle C}$ – емкость, в фарадах;
• ${\textstyle A}$ – площадь перекрытия двух плит, м²;
• ${\textstyle \varepsilon _{0}}$ электрическая постоянная ( ${\textstyle \varepsilon _{0}\approx 8.854\times 10^{-12}~\mathrm {F{\cdot }m^{-1}} }$);
• ${\textstyle \varepsilon _{r}}$ - относительная диэлектрическая проницаемость (также диэлектрическая проницаемость) материала между пластинами ( ${\textstyle \varepsilon _{r}\approx 1}$ для воздуха); и
• ${\textstyle d}$ расстояние между пластинами в метрах.

Уравнение является хорошим приближением, если d мало по сравнению с другими размерами пластин, так что электрическое поле в области конденсатора однородно, а так называемое краевое поле по периферии вносит лишь небольшой вклад в емкость.

Объединив уравнение емкости с приведенным выше уравнением энергии, запасенной в конденсаторе, для плоского конденсатора запасенная энергия составит:

$$W_{\text{stored}}={\frac {1}{2}}CV^{2}={\frac {1}{2}}\varepsilon {\frac {A}{d}}V^{2}.$$

где ${\textstyle W}$ – энергия, в джоулях; ${\textstyle C}$ – емкость, в фарадах; и ${\textstyle V}$ напряжение в вольтах.

Паразитная емкость

Основная статья: Паразитная емкость

Любые два соседних проводника могут функционировать как конденсатор, хотя емкость невелика, если только проводники не расположены близко друг к другу на больших расстояниях или на большой площади. Эту (часто нежелательную) емкость называют паразитной или паразитной емкостью. Паразитная емкость может привести к утечке сигналов между изолированными цепями (эффект, называемый перекрестными помехами ), и она может быть ограничивающим фактором для правильного функционирования цепей на высоких частотах .

Паразитная емкость между входом и выходом в схемах усилителя может создавать проблемы, поскольку она может образовывать путь обратной связи , что может вызвать нестабильность и паразитные колебания в усилителе. В аналитических целях часто бывает удобно заменить эту емкость комбинацией одной емкости «вход-земля» и одной емкости «выход-земля»; исходную конфигурацию, включая емкость входа-выхода, часто называют пи-конфигурацией. Для осуществления этой замены можно использовать теорему Миллера: она утверждает, что если коэффициент усиления двух узлов равен 1 / K , то импеданс Z , соединяющий два узла, можно заменить на Z / 1 − K сопротивление между первым узлом и землей и KZ / K − 1 полное сопротивление между вторым узлом и землей. Поскольку импеданс обратно пропорционален емкости, межузловая емкость C заменяется емкостью KC от входа до земли и емкостью ( K − 1) C / K от выхода к земле. Когда коэффициент усиления вход-выход очень велик, эквивалентное сопротивление вход-земля очень мало, в то время как сопротивление выход-земля по существу равно исходному импедансу (вход-выход).

Емкость проводников простой формы

Расчет емкости системы сводится к решению уравнения Лапласа ${\textstyle \nabla ^{2}\varphi =0}$ с постоянным потенциалом ${\textstyle \varphi }$ на двумерной поверхности проводников, встроенных в трехмерное пространство. Это упрощается симметриями. В более сложных случаях решения в терминах элементарных функций нет.

В плоских ситуациях аналитические функции могут использоваться для сопоставления различных геометрий друг с другом. См. также отображение Шварца – Кристоффеля .

Емкость простых систем

Тип	Емкость	Комментарий
Конденсатор с параллельными пластинами	$\ {\mathcal {C}}={\frac {\ \varepsilon A\ }{d}}\$	${\textstyle \varepsilon }$: Диэлектрическая проницаемость
Концентрические цилиндры	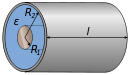$\ {\mathcal {C}}={\frac {2\pi \varepsilon \ell }{\ \ln \left(R_{2}/R_{1}\right)\ }}\$	${\textstyle \varepsilon }$: Диэлектрическая проницаемость
Эксцентриковые цилиндры	$\ {\mathcal {C}}={\frac {2\pi \varepsilon \ell }{\ \operatorname {arcosh} \left({\frac {R_{1}^{2}+R_{2}^{2}-d^{2}}{2R_{1}R_{2}}}\right)\ }}\$	${\textstyle \varepsilon }$: Диэлектрическая проницаемость ${\textstyle R_{1}}$: Внешний радиус ${\textstyle R_{2}}$: Внутренний радиус ${\textstyle d}$: Расстояние между центром ${\textstyle \ell }$: Длина провода
Пара параллельных проводов	$\ {\mathcal {C}}={\frac {\pi \varepsilon \ell }{\ \operatorname {arcosh} \left({\frac {d}{2a}}\right)\ }}={\frac {\pi \varepsilon \ell }{\ \ln \left({\frac {d}{\ 2a\ }}+{\sqrt {{\frac {d^{2}}{\ 4a^{2}\ }}-1\ }}\right)\ }}\$
Провод параллельно стене	$\ {\mathcal {C}}={\frac {2\pi \varepsilon \ell }{\ \operatorname {arcosh} \left({\frac {d}{a}}\right)\ }}={\frac {2\pi \varepsilon \ell }{\ \ln \left({\frac {\ d\ }{a}}+{\sqrt {{\frac {\ d^{2}\ }{a^{2}}}-1\ }}\right)\ }}\$	${\textstyle a}$: Радиус проволоки ${\textstyle d}$: Расстояние, ${\textstyle d>a}$ ${\textstyle \ell }$: Длина провода
Два параллельных копланарные полосы	$\ {\mathcal {C}}=\varepsilon \ell \ {\frac {\ K\left({\sqrt {1-k^{2}\ }}\right)\ }{K\left(k\right)}}\$	${\textstyle d}$: Расстояние ${\textstyle \ell }$: Длина ${\textstyle w_{1},w_{2}}$: Ширина полосы ${\textstyle \ k_{1}=\left({\tfrac {\ 2w_{1}\ }{d}}+1\right)^{-1}\ }$ $\ k_{2}=\left({\tfrac {\ 2w_{2}\ }{d}}+1\right)^{-1}\$$\ k={\sqrt {k_{1}\ k_{2}\ }}\$ ${\textstyle K}$: Полный эллиптический интеграл первого рода.
Концентрические сферы	$\ {\mathcal {C}}={\frac {4\pi \varepsilon }{\ {\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}\ }}\$	${\textstyle \varepsilon }$: Диэлектрическая проницаемость
Две сферы, равный радиус	${\begin{aligned}\ {\mathcal {C}}\ =&\ {}2\pi \varepsilon a\ \sum _{n=1}^{\infty }{\frac {\sinh \left(\ln \left(D+{\sqrt {D^{2}-1}}\right)\right)}{\sinh \left(n\ln \left(D+{\sqrt {D^{2}-1}}\right)\right)}}\\={}&{}2\pi \varepsilon a\left[1+{\frac {1}{2D}}+{\frac {1}{4D^{2}}}+{\frac {1}{8D^{3}}}+{\frac {1}{8D^{4}}}+{\frac {3}{32D^{5}}}+{\mathcal {O}}\left({\frac {1}{D^{6}}}\right)\right]\\={}&{}2\pi \varepsilon a\left[\ln 2+\gamma -{\frac {1}{2}}\ln \left(2D-2\right)+{\mathcal {O}}\left(2D-2\right)\right]\\={}&{}2\pi \varepsilon a\,{\frac {\sqrt {D^{2}-1}}{\log(q)}}\left[\psi _{q}\left(1+{\frac {i\pi }{\log(q)}}\right)-i\pi -\psi _{q}(1)\right]\end{aligned}}\$	${\textstyle a}$: Радиус ${\textstyle d}$: Расстояние, ${\textstyle d>2a}$ ${\textstyle D=d/2a,D>1}$ ${\textstyle \gamma }$: постоянная Эйлера $q=D+{\sqrt {D^{2}-1}}$ $\psi _{q}(z)={\frac {\partial _{z}\Gamma _{q}(z)}{\Gamma _{q}(z)}}$: q-дигамма-функция $\Gamma _{q}(z)$: функция q-гамма См. также Основные гипергеометрические ряды .
Сфера перед стеной	$\ {\mathcal {C}}=4\pi \varepsilon a\sum _{n=1}^{\infty }{\frac {\sinh \left(\ln \left(D+{\sqrt {D^{2}-1}}\right)\right)}{\sinh \left(n\ln \left(D+{\sqrt {D^{2}-1}}\right)\right)}}\$	$\ a\$: Радиус $\ d\$: Расстояние, $d>a$ $D=d/a$
Сфера	$\ {\mathcal {C}}=4\pi \varepsilon a\$	$a$: Радиус
Круглый диск	$\ {\mathcal {C}}=8\varepsilon a\$	$a$: Радиус
Тонкий прямой провод, конечная длина	$\ {\mathcal {C}}={\frac {2\pi \varepsilon \ell }{\Lambda }}\left[1+{\frac {1}{\Lambda }}\left(1-\ln 2\right)+{\frac {1}{\Lambda ^{2}}}\left(1+\left(1-\ln 2\right)^{2}-{\frac {\pi ^{2}}{12}}\right)+{\mathcal {O}}\left({\frac {1}{\Lambda ^{3}}}\right)\right]\$	$a$: Радиус проволоки $\ell$: Длина $\ \Lambda =\ln \left(\ell /a\right)\$

Хранение энергии

Энергия ) , (измеренная в джоулях запасенная в конденсаторе, равна работе , необходимой для проталкивания зарядов в конденсатор, то есть для его зарядки. Рассмотрим конденсатор емкостью C , удерживающий заряд + q на одной пластине и − q на другой. Перемещение небольшого элемента заряда d q с одной пластины на другую против разности потенциалов V = q / C требует работы d W :

$$\mathrm {d} W={\frac {q}{C}}\,\mathrm {d} q,$$

где W — работа, измеряемая в джоулях, q — заряд, измеряемый в кулонах, а C — емкость, измеряемая в фарадах.

Энергия, запасенная в конденсаторе, находится путем интегрирования этого уравнения. Начиная с незаряженной емкости ( q = 0 ) и перемещая заряд от одной пластины к другой до тех пор, пока пластины не приобретут заряд + Q и − Q, требуется работа W :

$$W_{\text{charging}}=\int _{0}^{Q}{\frac {q}{C}}\,\mathrm {d} q={\frac {1}{2}}{\frac {Q^{2}}{C}}={\frac {1}{2}}QV={\frac {1}{2}}CV^{2}=W_{\text{stored}}.$$

системы

Емкость наноразмерных диэлектрических конденсаторов, таких как квантовые точки, может отличаться от емкости обычных конденсаторов большего размера. В частности, разность электростатических потенциалов, испытываемая электронами в обычных конденсаторах, пространственно четко определена и фиксируется формой и размером металлических электродов в дополнение к статистически большому количеству электронов, присутствующих в обычных конденсаторах. Однако в наноразмерных конденсаторах электростатические потенциалы, испытываемые электронами, определяются количеством и расположением всех электронов, которые вносят вклад в электронные свойства устройства. В таких устройствах количество электронов может быть очень небольшим, поэтому результирующее пространственное распределение эквипотенциальных поверхностей внутри устройства чрезвычайно сложное.

Одноэлектронные устройства

Емкость подключенного, или «закрытого», одноэлектронного устройства в два раза превышает емкость несвязанного, или «открытого», одноэлектронного устройства. Более фундаментально этот факт можно объяснить энергией, запасенной в одноэлектронном устройстве, энергия взаимодействия «прямой поляризации» которого может быть поровну разделена на взаимодействие электрона с поляризованным зарядом на самом устройстве из-за присутствия электрона и количество потенциальной энергии, необходимой для образования поляризованного заряда на устройстве (взаимодействие зарядов в диэлектрическом материале устройства с потенциалом, обусловленным электроном).

Малоэлектронные устройства

При выводе «квантовой емкости» малоэлектронного устройства используется термодинамический химический потенциал системы N -частиц, определяемый выражением

$$\mu (N)=U(N)-U(N-1),$$

чьи энергетические члены могут быть получены как решения уравнения Шредингера. Определение емкости,

$${1 \over C}\equiv {\Delta V \over \Delta Q},$$

с разницей потенциалов

$$\Delta V={\Delta \mu \, \over e}={\mu (N+\Delta N)-\mu (N) \over e}$$

может быть применено устройство с добавлением или удалением отдельных электронов,

$$\Delta N=1$$

и

$$\Delta Q=e.$$

Тогда «квантовая емкость» устройства равна

$$C_{Q}(N)={\frac {e^{2}}{\mu (N+1)-\mu (N)}}={\frac {e^{2}}{E(N)}}.$$

Это выражение «квантовой емкости» можно записать как

$$C_{Q}(N)={e^{2} \over U(N)},$$

которое отличается от общепринятого выражения, описанного во введении, где $W_{\text{stored}}=U$, запасенная электростатическая потенциальная энергия,

$$C={Q^{2} \over 2U},$$

в разы 1/2 ​ ​ с $Q=Ne$.

Однако в рамках чисто классических электростатических взаимодействий появление фактора 1/2 конденсатора , — результат интегрирования в общепринятой формулировке, учитывающей работу, совершаемую при зарядке

$$W_{\text{charging}}=U=\int _{0}^{Q}{\frac {q}{C}}\,\mathrm {d} q,$$

что уместно, поскольку $\mathrm {d} q=0$ для систем с множеством электронов или с металлическими электродами, но в системах с небольшим количеством электронов $\mathrm {d} q\to \Delta \,Q=e$. Интеграл обычно превращается в сумму. Можно тривиально объединить выражения емкости

$$Q=CV$$

и энергия электростатического взаимодействия,

$$U=QV,$$

чтобы получить

$$C=Q{1 \over V}=Q{Q \over U}={Q^{2} \over U},$$

что аналогично квантовой емкости. В литературе приводится более строгий вывод. В частности, чтобы обойти математические проблемы, связанные с пространственно сложными эквипотенциальными поверхностями внутри устройства, средний при выводе используется электростатический потенциал, испытываемый каждым электроном.

Очевидные математические различия можно понять более фундаментально. Потенциальная энергия, $U(N)$, изолированного устройства (собственная емкость) в два раза больше, чем сохраненное в «подключенном» устройстве в нижнем пределе $N=1$. Как $N$ вырастает большим, $U(N)\to U$. Таким образом, общее выражение емкости имеет вид

$$C(N)={(Ne)^{2} \over U(N)}.$$

В наноразмерных устройствах, таких как квантовые точки, «конденсатор» часто представляет собой изолированный или частично изолированный компонент внутри устройства. Основные различия между наноразмерными конденсаторами и макроскопическими (обычными) конденсаторами заключаются в количестве избыточных электронов (носителей заряда или электронов, которые вносят вклад в электронное поведение устройства), а также в форме и размере металлических электродов. В наноразмерных устройствах нанопроволоки , состоящие из атомов металлов, обычно не обладают теми же проводящими свойствами, что и их макроскопические или объемные материальные аналоги.

Емкость в электронных и полупроводниковых устройствах

В электронных и полупроводниковых устройствах переходный или частотно-зависимый ток между клеммами содержит компоненты проводимости и смещения. Ток проводимости связан с движущимися носителями заряда (электронами, дырками, ионами и т. д.), тогда как ток смещения вызывается изменяющимся во времени электрическим полем. На транспорт носителей влияют электрические поля и ряд физических явлений, таких как дрейф и диффузия носителей, захват, инжекция, контактные эффекты, ударная ионизация и т. д. В результате проводимость устройства зависит от частоты, и простой электростатическая формула емкости $C=q/V,$ не применимо. Более общее определение емкости, включающее электростатическую формулу, выглядит следующим образом:

$$C={\frac {\operatorname {Im} (Y(\omega ))}{\omega }},$$

где $Y(\omega )$ - это допуск устройства, и $\omega$ - угловая частота.

В общем, емкость является функцией частоты. На высоких частотах емкость приближается к постоянному значению, равному «геометрической» емкости, определяемой геометрией клемм и содержанием диэлектрика в устройстве.Статья Стивена Ло представлен обзор численных методов расчета емкости. В частности, емкость можно рассчитать с помощью преобразования Фурье переходного тока в ответ на ступенчатое возбуждение напряжением:

$$C(\omega )={\frac {1}{\Delta V}}\int _{0}^{\infty }[i(t)-i(\infty )]\cos(\omega t)dt.$$

Отрицательная емкость в полупроводниковых приборах

Обычно емкость полупроводниковых приборов положительна. Однако в некоторых устройствах и при определенных условиях (температура, приложенное напряжение, частота и т. д.) емкость может стать отрицательной. Немонотонное поведение переходного тока в ответ на ступенчатое возбуждение было предложено как механизм отрицательной емкости. Отрицательная емкость была продемонстрирована и исследована во многих различных типах полупроводниковых устройств.

Измерение емкости

Основная статья: Измеритель емкости

Измеритель емкости — это электронное испытательное оборудование, используемое для измерения емкости, в основном дискретных конденсаторов . В большинстве случаев и в большинстве случаев конденсатор необходимо отключить от цепи .

Многие цифровые вольтметры ( цифровые вольтметры ) имеют функцию измерения емкости. Обычно они работают путем зарядки и разрядки испытуемого конденсатора известным током и измерения скорости нарастания результирующего напряжения ; чем медленнее скорость нарастания, тем больше емкость. Цифровые вольтметры обычно могут измерять емкость от нанофарад до нескольких сотен микрофарад, но более широкие диапазоны не являются чем-то необычным. Также можно измерить емкость, пропуская известный переменный высокочастотный ток через испытуемое устройство и измеряя на нем результирующее напряжение (не работает для поляризованных конденсаторов).

Andeen -Hagerling 2700A. Емкостной мост

В более сложных приборах используются другие методы, такие как включение тестируемого конденсатора в мостовую схему . Варьируя номиналы других ветвей моста (чтобы привести мост в равновесие), определяют номинал неизвестного конденсатора. Этот метод косвенного использования измерения емкости обеспечивает большую точность. Благодаря использованию соединений Кельвина и других методов тщательного проектирования эти приборы обычно могут измерять конденсаторы в диапазоне от пикофарад до фарад.

См. также

• Емкостный датчик перемещения
• Емкость комплекта
• Ток смещения
• закон Гаусса
• LCR-метр
• Магнитоемкость
• Квантовая емкость

Дальнейшее чтение

• Типлер, Пол (1998). Физика для ученых и инженеров: Vol. 2: Электричество и магнетизм, Свет (4-е изд.). У. Х. Фриман. ISBN   1-57259-492-6
• Сервей, Раймонд; Джуэтт, Джон (2003). Физика для ученых и инженеров (6-е изд.). Брукс Коул. ISBN   0-534-40842-7
• Саслоу, Уэйн М. (2002). Электричество, магнетизм и свет . Томсон Обучение. ISBN   0-12-619455-6 . См. главу 8 и особенно стр. 255–259 о коэффициентах потенциала.

Внешние ссылки

• СМИ, связанные с емкостью, на Викискладе?