Закон Гаусса

Эта статья о законе Гаусса об электрическом поле. Аналогичные законы, касающиеся различных полей, см. в законе Гаусса для магнетизма и в законе Гаусса для гравитации . Информацию о теореме Остроградского-Гаусса, математической теореме, относящейся ко всем этим законам, см. в разделе « Теорема о дивергенции» .

Не путать с законом Гаузе .

Закон Гаусса в его интегральной форме особенно полезен, когда по соображениям симметрии можно найти замкнутую поверхность (ЗС), вдоль которой электрическое поле однородно. Тогда электрический поток представляет собой простое произведение площади поверхности и напряженности электрического поля и пропорционален общему заряду, заключенному в поверхности. электрическое поле снаружи ( r > R ) и внутри ( r < R Здесь рассчитывается ) заряженной сферы (см. Викиверситет ).

В физике (в частности , в электромагнетизме ) закон Гаусса , также известный как теорема Гаусса о потоке (или иногда теорема Гаусса), является одним из уравнений Максвелла . Он связывает распределение электрического заряда с результирующим электрическим полем .

Определение

В своей интегральной форме он утверждает, что поток электрического поля из произвольной замкнутой поверхности пропорционален электрическому заряду, заключенному в этой поверхности, независимо от того, как этот заряд распределен. Хотя одного закона недостаточно для определения электрического поля на поверхности, охватывающей любое распределение заряда, это может быть возможно в тех случаях, когда симметрия требует однородности поля. Там, где такой симметрии не существует, можно использовать закон Гаусса в его дифференциальной форме , которая гласит, что дивергенция электрического поля пропорциональна локальной плотности заряда.

Закон был первым сформулированный Жозефом-Луи Лагранжем в 1773 году, за ним последовал Карл Фридрих Гаусс в 1835 году, как в контексте притяжения эллипсоидов. Это одно из уравнений Максвелла , составляющее основу классической электродинамики . Закон Гаусса можно использовать для вывода закона Кулона . и наоборот.

Качественное описание

На словах закон Гаусса гласит:

Чистый электрический поток через любую гипотетическую замкнутую поверхность равен 1/ ε0 _, умноженному на чистый электрический заряд, заключенный внутри этой замкнутой поверхности. Замкнутую поверхность также называют поверхностью Гаусса.

Закон Гаусса имеет близкое математическое сходство с рядом законов в других областях физики, таких как закон Гаусса для магнетизма и закон Гаусса для гравитации . Фактически, любой закон обратных квадратов может быть сформулирован аналогично закону Гаусса: например, сам закон Гаусса по существу эквивалентен закону Кулона , а закон Гаусса для гравитации по существу эквивалентен закону гравитации Ньютона , оба из которых которые представляют собой законы обратных квадратов.

Закон можно выразить математически с помощью векторного исчисления в интегральной и дифференциальной форме; оба эквивалентны, поскольку они связаны теоремой о дивергенции , также называемой теоремой Гаусса. Каждая из этих форм, в свою очередь, также может быть выражена двумя способами: через связь между электрическим полем Е и полным электрическим зарядом или через электрическое поле смещения D и свободный электрический заряд .

Уравнение с E полем

Закон Гаусса можно сформулировать, используя либо электрическое поле , либо поле электрического смещения D. E В этом разделе показаны некоторые формы с E ; форма с D приведена ниже, как и другие формы с E .

Интегральная форма

Электрический поток через произвольную поверхность пропорционален общему заряду, заключенному в этой поверхности.

Никакой заряд не заключен в сфере. Электрический поток через его поверхность равен нулю.

Закон Гаусса можно выразить так:

$$\Phi _{E}={\frac {Q}{\varepsilon _{0}}}$$

где Φ _E — электрический поток через замкнутую поверхность S, охватывающую любой объем V , Q — полный заряд, заключенный внутри V , а ε ₀ — электрическая постоянная . Электрический поток Φ _E определяется как поверхностный интеграл электрического поля:

$\Phi _{E}=$ $\scriptstyle _{S}$ $\mathbf {E} \cdot \mathrm {d} \mathbf {A}$

где E — электрическое поле, d A — вектор, представляющий бесконечно малый элемент площади поверхности, и · представляет собой скалярное произведение двух векторов.

В искривленном пространстве-времени поток электромагнитного поля через замкнутую поверхность выражается как

$\Phi _{E}=c$ $\scriptstyle _{S}$ $F^{\kappa 0}{\sqrt {-g}}\,\mathrm {d} S_{\kappa }$

где $c$ — скорость света ; $F^{\kappa 0}$ обозначает временные компоненты электромагнитного тензора ; $g$ – определитель метрического тензора ; $\mathrm {d} S_{\kappa }=\mathrm {d} S^{ij}=\mathrm {d} x^{i}\mathrm {d} x^{j}$ — ортонормированный элемент двумерной поверхности, окружающей заряд $Q$; индексы $i,j,\kappa =1,2,3$ и не подходят друг другу.

Поскольку поток определяется как интеграл от электрического поля, это выражение закона Гаусса называется интегральной формой .

Крошечный ящик Гаусса, стороны которого перпендикулярны поверхности проводника, используется для определения локального поверхностного заряда после расчета электрического потенциала и электрического поля путем решения уравнения Лапласа. Электрическое поле локально перпендикулярно эквипотенциальной поверхности проводника и равно нулю внутри; его поток πa ² · E по закону Гаусса равна πa ² · с / е ₀ . Таким образом, σ = ε ₀ E .

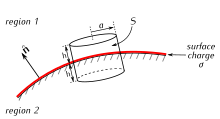
В задачах, связанных с проводниками, имеющими известные потенциалы, потенциал вдали от них получается путем решения уравнения Лапласа аналитически или численно. Затем электрическое поле рассчитывается как отрицательный градиент потенциала. Закон Гаусса позволяет найти распределение электрического заряда: заряд в любой заданной области проводника можно определить, проинтегрировав электрическое поле и найдя поток через небольшой ящик, стороны которого перпендикулярны поверхности проводника, и отметив, что электрическое поле перпендикулярно поверхности и равно нулю внутри проводника.

Обратная задача, когда известно распределение электрического заряда и необходимо рассчитать электрическое поле, гораздо сложнее. Полный поток через данную поверхность дает мало информации об электрическом поле и может входить и выходить из поверхности по сколь угодно сложным схемам.

Исключение составляют случаи, когда в задаче присутствует некоторая симметрия , которая требует, чтобы электрическое поле проходило через поверхность равномерно. Тогда, если известен полный поток, само поле можно определить в каждой точке. Общие примеры симметрии, подпадающие под действие закона Гаусса, включают: цилиндрическую симметрию, плоскую симметрию и сферическую симметрию. См. статью «Гауссова поверхность» , где приведены примеры использования этих симметрий для расчета электрических полей.

Дифференциальная форма

По теореме о дивергенции закон Гаусса альтернативно можно записать в дифференциальной форме : $$\nabla \cdot \mathbf {E} ={\frac {\rho }{\varepsilon _{0}}}$$

где ∇ · E — дивергенция электрического поля, ε ₀ — диэлектрическая проницаемость вакуума и ρ — полная объемная плотность заряда (заряд на единицу объема).

Эквивалентность интегральной и дифференциальной форм

Основная статья: Теорема о дивергенции

По теореме о дивергенции интегральная и дифференциальная формы математически эквивалентны. Вот аргумент более конкретно.

Схема доказательства

Интегральная форма закона Гаусса:

${\scriptstyle _{S}}$ $\mathbf {E} \cdot \mathrm {d} \mathbf {A}$$={\frac {Q}{\varepsilon _{0}}}$

для любой замкнутой поверхности S, заряд Q. содержащей По теореме о дивергенции это уравнение эквивалентно:

$$\iiint _{V}\nabla \cdot \mathbf {E} \,\mathrm {d} V={\frac {Q}{\varepsilon _{0}}}$$

для любого объема V, заряд Q. содержащего По соотношению между зарядом и плотностью заряда это уравнение эквивалентно: $$\iiint _{V}\nabla \cdot \mathbf {E} \,\mathrm {d} V=\iiint _{V}{\frac {\rho }{\varepsilon _{0}}}\,\mathrm {d} V$$для любого объема V . Для того чтобы это уравнение было одновременно верным для любого возможного объема V , необходимо (и достаточно), чтобы подынтегральные выражения были повсюду равны. Следовательно, это уравнение эквивалентно:

$$\nabla \cdot \mathbf {E} ={\frac {\rho }{\varepsilon _{0}}}.$$Таким образом, интегральная и дифференциальная формы эквивалентны.

Уравнение, включающее D поле

Смотрите также: уравнения Максвелла

Бесплатно, связанно и за полную плату

Основная статья: Электрическая поляризация

Электрический заряд, который возникает в простейших учебниковых ситуациях, можно было бы классифицировать как «свободный заряд» — например, заряд, который передается в статическом электричестве , или заряд на пластине конденсатора . Напротив, «связанный заряд» возникает только в случае диэлектрических (поляризующихся) материалов. (Все материалы в некоторой степени поляризуемы.) Когда такие материалы помещаются во внешнее электрическое поле, электроны остаются связанными с соответствующими атомами, но смещаются на микроскопическое расстояние под действием поля, так что они оказываются больше на одной стороне. атома, чем другой. Все эти микроскопические смещения в сумме дают макроскопическое распределение суммарного заряда, и это составляет «связанный заряд».

Хотя микроскопически все заряды по сути одинаковы, часто существуют практические причины рассматривать связанный заряд иначе, чем свободный заряд. В результате более фундаментальный закон Гаусса в терминах E (выше) иногда приводится в эквивалентную форму ниже, которая выражается только в терминах D и свободного заряда.

Интегральная форма

Эта формулировка закона Гаусса определяет форму полного заряда:

$$\Phi _{D}=Q_{\mathrm {free} }$$

где Φ _D — поток D -поля через поверхность S охватывающую объем V , а Q _free — свободный заряд, содержащийся в V. , Поток Φ _D определяется аналогично потоку Φ _E электрического поля E через S :

$\Phi _{D}=$ ${\scriptstyle _{S}}$ $\mathbf {D} \cdot \mathrm {d} \mathbf {A}$

Дифференциальная форма

Дифференциальная форма закона Гаусса, включающая только бесплатный заряд, гласит: $$\nabla \cdot \mathbf {D} =\rho _{\mathrm {free} }$$

где ∇ · D — дивергенция поля электрического смещения, а ρ _free — плотность свободного электрического заряда.

Эквивалентность отчетов об общих и бесплатных расходах

Доказательство того, что формулировки закона Гаусса в терминах свободного заряда эквивалентны формулировкам, включающим полный заряд.

В этом доказательстве мы покажем, что уравнение $$\nabla \cdot \mathbf {E} ={\dfrac {\rho }{\varepsilon _{0}}}$$эквивалентно уравнению $$\nabla \cdot \mathbf {D} =\rho _{\mathrm {free} }$$Обратите внимание, что мы имеем дело только с дифференциальными формами, а не с интегральными формами, но этого достаточно, поскольку дифференциальная и интегральная формы эквивалентны в каждом случае по теореме о расходимости.

Введем плотность поляризации P , которая имеет следующую связь с E и D : $$\mathbf {D} =\varepsilon _{0}\mathbf {E} +\mathbf {P}$$и следующее отношение к связанному заряду: $$\rho _{\mathrm {bound} }=-\nabla \cdot \mathbf {P}$$Теперь рассмотрим три уравнения: $${\begin{aligned}\rho _{\mathrm {bound} }&=\nabla \cdot (-\mathbf {P} )\\\rho _{\mathrm {free} }&=\nabla \cdot \mathbf {D} \\\rho &=\nabla \cdot (\varepsilon _{0}\mathbf {E} )\end{aligned}}$$Ключевой вывод заключается в том, что сумма первых двух уравнений является третьим уравнением. Это завершает доказательство: первое уравнение истинно по определению, и, следовательно, второе уравнение истинно тогда и только тогда, когда верно третье уравнение. Итак, второе и третье уравнения эквивалентны, что мы и хотели доказать.

Уравнение для линейных материалов

В однородных , изотропных , недисперсионных , линейных материалах существует простая связь между E и D :

$$\mathbf {D} =\varepsilon \mathbf {E}$$

где ε — диэлектрическая проницаемость материала. В случае вакуума (так называемого свободного пространства ) ε = ε ₀ . В этих обстоятельствах закон Гаусса изменяется на

$$\Phi _{E}={\frac {Q_{\mathrm {free} }}{\varepsilon }}$$

для интегральной формы и

$$\nabla \cdot \mathbf {E} ={\frac {\rho _{\mathrm {free} }}{\varepsilon }}$$

для дифференциальной формы.

Связь с законом Кулона

Вывод закона Гаусса из закона Кулона.

Строго говоря, закон Гаусса не может быть выведен только из закона Кулона, поскольку закон Кулона дает электрическое поле только за счет отдельного электростатического точечного заряда . Однако закон Гаусса можно доказать из закона Кулона, если предположить, кроме того, что электрическое поле подчиняется принципу суперпозиции . Принцип суперпозиции гласит, что результирующее поле представляет собой векторную сумму полей, создаваемых каждой частицей (или интеграл, если заряды равномерно распределены в пространстве).

Схема доказательства

Закон Кулона гласит, что электрическое поле, создаваемое неподвижным точечным зарядом , равно: $$\mathbf {E} (\mathbf {r} )={\frac {q}{4\pi \varepsilon _{0}}}{\frac {\mathbf {e} _{r}}{r^{2}}}$$где

• e _r — радиальный единичный вектор ,
• r — радиус, | р | ,
• ε ₀ — электрическая постоянная ,
• q — заряд частицы, которая предполагается находящейся в начале координат .

Используя выражение из закона Кулона, мы получаем полное поле в точке r , используя интеграл для суммирования поля в точке r, обусловленного бесконечно малыми зарядами в каждой точке s в пространстве, что дает $$\mathbf {E} (\mathbf {r} )={\frac {1}{4\pi \varepsilon _{0}}}\int {\frac {\rho (\mathbf {s} )(\mathbf {r} -\mathbf {s} )}{|\mathbf {r} -\mathbf {s} |^{3}}}\,\mathrm {d} ^{3}\mathbf {s}$$где ρ — плотность заряда. Если мы возьмем расходимость обеих частей этого уравнения по r и воспользуемся известной теоремой

$$\nabla \cdot \left({\frac {\mathbf {r} }{|\mathbf {r} |^{3}}}\right)=4\pi \delta (\mathbf {r} )$$где δ ( r ) — дельта-функция Дирака , результат: $$\nabla \cdot \mathbf {E} (\mathbf {r} )={\frac {1}{\varepsilon _{0}}}\int \rho (\mathbf {s} )\,\delta (\mathbf {r} -\mathbf {s} )\,\mathrm {d} ^{3}\mathbf {s}$$

Используя « свойство просеивания » дельта-функции Дирака, мы приходим к $$\nabla \cdot \mathbf {E} (\mathbf {r} )={\frac {\rho (\mathbf {r} )}{\varepsilon _{0}}},$$что является дифференциальной формой закона Гаусса, как и хотелось.

Поскольку закон Кулона применим только к стационарным зарядам, нет оснований ожидать, что закон Гаусса будет справедливым и для движущихся зарядов, основываясь только на этом выводе. Фактически закон Гаусса справедлив для движущихся зарядов, и в этом отношении закон Гаусса является более общим, чем закон Кулона.

Доказательство (без Дельты Дирака)

Позволять $\Omega \subseteq R^{3}$ быть ограниченным открытым множеством и $$\mathbf {E} _{0}(\mathbf {r} )={\frac {1}{4\pi \varepsilon _{0}}}\int _{\Omega }\rho (\mathbf {r} '){\frac {\mathbf {r} -\mathbf {r} '}{\left\|\mathbf {r} -\mathbf {r} '\right\|^{3}}}\mathrm {d} \mathbf {r} '\equiv {\frac {1}{4\pi \varepsilon _{0}}}\int _{\Omega }e(\mathbf {r,\mathbf {r} '} ){\mathrm {d} \mathbf {r} '}$$ быть электрическим полем, причем $\rho (\mathbf {r} ')$ непрерывная функция (плотность заряда).

Это верно для всех $\mathbf {r} \neq \mathbf {r'}$ что $\nabla _{\mathbf {r} }\cdot \mathbf {e} (\mathbf {r,r'} )=0$.

Рассмотрим теперь компакт $V\subseteq R^{3}$ имеющий кусочно гладкую границу $\partial V$ такой, что $\Omega \cap V=\emptyset$. Отсюда следует, что $e(\mathbf {r,\mathbf {r} '} )\in C^{1}(V\times \Omega )$ и так, для теоремы о расходимости:

$$\oint _{\partial V}\mathbf {E} _{0}\cdot d\mathbf {S} =\int _{V}\mathbf {\nabla } \cdot \mathbf {E} _{0}\,dV$$

Но потому что $e(\mathbf {r,\mathbf {r} '} )\in C^{1}(V\times \Omega )$,

$$\mathbf {\nabla } \cdot \mathbf {E} _{0}(\mathbf {r} )={\frac {1}{4\pi \varepsilon _{0}}}\int _{\Omega }\nabla _{\mathbf {r} }\cdot e(\mathbf {r,\mathbf {r} '} ){\mathrm {d} \mathbf {r} '}=0$$ для аргумента выше ( $\Omega \cap V=\emptyset \implies \forall \mathbf {r} \in V\ \ \forall \mathbf {r'} \in \Omega \ \ \ \mathbf {r} \neq \mathbf {r'}$ а потом $\nabla _{\mathbf {r} }\cdot \mathbf {e} (\mathbf {r,r'} )=0$)

Следовательно, поток через замкнутую поверхность, создаваемый некоторой плотностью заряда снаружи (поверхности), равен нулю.

Теперь рассмотрим $\mathbf {r} _{0}\in \Omega$, и $B_{R}(\mathbf {r} _{0})\subseteq \Omega$ как сфера с центром в $\mathbf {r} _{0}$ имея $R$ как радиус (он существует, потому что $\Omega$ является открытым множеством).

Позволять $\mathbf {E} _{B_{R}}$ и $\mathbf {E} _{C}$ быть электрическим полем, созданным внутри и снаружи сферы соответственно. Затем,

$\mathbf {E} _{B_{R}}={\frac {1}{4\pi \varepsilon _{0}}}\int _{B_{R}(\mathbf {r} _{0})}e(\mathbf {r,\mathbf {r} '} ){\mathrm {d} \mathbf {r} '}$, $\mathbf {E} _{C}={\frac {1}{4\pi \varepsilon _{0}}}\int _{\Omega \setminus B_{R}(\mathbf {r} _{0})}e(\mathbf {r,\mathbf {r} '} ){\mathrm {d} \mathbf {r} '}$ и $\mathbf {E} _{B_{R}}+\mathbf {E} _{C}=\mathbf {E} _{0}$

$$\Phi (R)=\oint _{\partial B_{R}(\mathbf {r} _{0})}\mathbf {E} _{0}\cdot d\mathbf {S} =\oint _{\partial B_{R}(\mathbf {r} _{0})}\mathbf {E} _{B_{R}}\cdot d\mathbf {S} +\oint _{\partial B_{R}(\mathbf {r} _{0})}\mathbf {E} _{C}\cdot d\mathbf {S} =\oint _{\partial B_{R}(\mathbf {r} _{0})}\mathbf {E} _{B_{R}}\cdot d\mathbf {S}$$

Последнее равенство следует из наблюдения, что $(\Omega \setminus B_{R}(\mathbf {r} _{0}))\cap B_{R}(\mathbf {r} _{0})=\emptyset$и аргумент выше.

RHS — это электрический поток, создаваемый заряженной сферой, поэтому:

$$\Phi (R)={\frac {Q(R)}{\varepsilon _{0}}}={\frac {1}{\varepsilon _{0}}}\int _{B_{R}(\mathbf {r} _{0})}\rho (\mathbf {r} '){\mathrm {d} \mathbf {r} '}={\frac {1}{\varepsilon _{0}}}\rho (\mathbf {r} '_{c})|B_{R}(\mathbf {r} _{0})|$$ с $r'_{c}\in \ B_{R}(\mathbf {r} _{0})$

Где последнее равенство следует из теоремы о среднем значении для интегралов. Используя теорему сжатия и непрерывность $\rho$, получаем:

$$\mathbf {\nabla } \cdot \mathbf {E} _{0}(\mathbf {r} _{0})=\lim _{R\to 0}{\frac {1}{|B_{R}(\mathbf {r} _{0})|}}\Phi (R)={\frac {1}{\varepsilon _{0}}}\rho (\mathbf {r} _{0})$$

Вывод закона Кулона из закона Гаусса.

Строго говоря, закон Кулона не может быть выведен только из закона Гаусса, поскольку закон Гаусса не дает никакой информации относительно ротора Е ( разложение см. Гельмгольца и закон Фарадея ). Однако закон Кулона можно доказать из закона Гаусса, если дополнительно предположить, что электрическое поле от точечного заряда сферически симметрично (это предположение, как и сам закон Кулона, в точности верно, если заряд стационарен, и приблизительно верно если заряд находится в движении).

Схема доказательства

Принимая S в интегральной форме закона Гаусса за сферическую поверхность радиуса r с центром в точечном заряде Q , мы имеем

$$\oint _{S}\mathbf {E} \cdot d\mathbf {A} ={\frac {Q}{\varepsilon _{0}}}$$

В предположении сферической симметрии подынтегральная функция является константой, которую можно вынести из интеграла. Результат $$4\pi r^{2}{\hat {\mathbf {r} }}\cdot \mathbf {E} (\mathbf {r} )={\frac {Q}{\varepsilon _{0}}}$$где r̂ — единичный вектор, направленный радиально от заряда. Опять же, согласно сферической симметрии, E указывает в радиальном направлении, и поэтому мы получаем $$\mathbf {E} (\mathbf {r} )={\frac {Q}{4\pi \varepsilon _{0}}}{\frac {\hat {\mathbf {r} }}{r^{2}}}$$что по сути эквивалентно закону Кулона. Таким образом, зависимость электрического поля по закону обратных квадратов в законе Кулона следует из закона Гаусса.

См. также

• Метод оплаты имиджа
• Теорема единственности уравнения Пуассона
• Список примеров закона Стиглера

Ссылки

• Гаусс, Карл Фридрих (1867). Сочинения Том 5 . Цифровая версия
• Джексон, Джон Дэвид (1998). Классическая электродинамика (3-е изд.). Нью-Йорк: Уайли. ISBN  0-471-30932-Х . Дэвид Дж. Гриффитс (6-е изд.)

Внешние ссылки

• СМИ, связанные с законом Гаусса, на Викискладе?
• Серия видеолекций MIT (30 лекций по 50 минут) — Электричество и магнетизм, преподаваемые профессором Уолтером Левином .
• раздел о законе Гаусса в онлайн-учебнике. Архивировано 27 мая 2010 г. в Wayback Machine.
• MISN-0-132 Закон Гаусса для сферической симметрии ( файл PDF ), автор Питер Сигнелл для проекта PHYSNET .
• MISN-0-133 Закон Гаусса в применении к цилиндрическим и плоским распределениям заряда (файл PDF), Питер Сигнелл для проекта PHYSNET .