Дифференциальная геометрия поверхностей

«Риманова поверхность» перенаправляется сюда. Не путать с римановой поверхностью .

Карл Фридрих Гаусс в 1828 году.

В математике дифференциальная геометрия поверхностей имеет дело с дифференциальной геометрией гладких поверхностей римановой с различными дополнительными структурами, чаще всего — метрикой . Поверхности широко изучались с различных точек зрения: внешне , в связи с их погружением в евклидово пространство , и внутренне , отражая их свойства, определяемые исключительно расстоянием внутри поверхности, измеренным вдоль кривых на поверхности. Одной из фундаментальных исследуемых концепций является гауссова кривизна , впервые подробно изученная Карлом Фридрихом Гауссом . который показал, что кривизна является внутренним свойством поверхности, независимым от ее изометрического вложения в евклидово пространство.

Поверхности естественным образом возникают как графики функций , пары переменных , а иногда появляются в параметрической форме или как локусы связанные с пространственными кривыми . Важную роль в их изучении сыграли группы Ли (в духе Эрлангенской программы ), а именно группы симметрии евклидовой плоскости , сферы и гиперболической плоскости . Эти группы Ли можно использовать для описания поверхностей постоянной гауссовой кривизны; они также являются важным компонентом современного подхода к внутренней дифференциальной геометрии через связи . С другой стороны, внешние свойства, основанные на вложении поверхности в евклидово пространство, также широко изучались. Это хорошо иллюстрируется нелинейными уравнениями Эйлера-Лагранжа в вариационном исчислении : хотя Эйлер разработал уравнения с одной переменной для понимания геодезических , определенных независимо от вложения, одно из основных применений Лагранжа уравнений с двумя переменными было к минимальным поверхностям. , концепция, которую можно определить только с точки зрения вложения.

История

Бернхард Риман (1826-1866)

Объемы некоторых квадратичных поверхностей были вращения вычислены Архимедом . Развитие исчисления в семнадцатом веке обеспечило более систематический способ их вычисления. Кривизну общих поверхностей впервые изучил Эйлер . В 1760 году он доказал формулу кривизны плоского сечения поверхности и в 1771 г. он рассматривал поверхности, представленные в параметрической форме. Монж заложил основы их теории в своих классических мемуарах «Применение анализа в геометрии» , вышедших в 1795 году. Определяющий вклад в теорию поверхностей был внесен Гауссом в двух замечательных статьях, написанных в 1825 и 1827 годах. Это ознаменовало новый отход от традиции, поскольку Гаусс впервые рассмотрел внутреннюю геометрию поверхности, свойства которой определяются только геодезическими расстояниями между точками на поверхности, независимо от того, каким образом поверхность расположена в окружающей среде. Евклидово пространство. Венчающий результат, Теорема Эгрегиума Гаусса, установил, что гауссова кривизна является внутренним инвариантом, то есть инвариантом относительно локальных изометрий . на многомерные пространства Эта точка зрения была распространена Риманом и привела к тому, что сегодня известно как риманова геометрия . Девятнадцатый век был золотым веком теории поверхностей как с топологической, так и с дифференциально-геометрической точки зрения, и большинство ведущих геометров посвятили себя их изучению. Дарбу собрал множество результатов в своем четырехтомном трактате «Теория поверхностей» (1887–1896).

Обзор

Для более широкого освещения этой темы см. Поверхность (математика) .

Интуитивно вполне привычно сказать, что лист растения, поверхность стекла или форма лица изогнуты определенным образом и что все эти формы, даже если игнорировать какие-либо отличительные признаки, имеют определенные геометрические особенности. особенности, отличающие одно от другого. Дифференциальная геометрия поверхностей занимается математическим пониманием таких явлений. Изучение этой области, начатое в ее современной форме в 1700-х годах, привело к развитию многомерной и абстрактной геометрии, такой как риманова геометрия и общая теория относительности .

Основным математическим объектом является регулярная поверхность. Хотя соглашения различаются в своем точном определении, они образуют общий класс подмножеств трехмерного евклидова пространства ( ℝ ³ ), которые отражают часть знакомого понятия «поверхность». Анализируя класс кривых, лежащих на такой поверхности, и степень, в которой поверхности заставляют их искривляться в ℝ ³ , каждой точке поверхности можно сопоставить два числа, называемые главными кривизнами. Их среднее значение называется средней кривизной поверхности, а их произведение — гауссовой кривизной.

Существует множество классических примеров регулярных поверхностей, в том числе:

• знакомые примеры, такие как плоскости, цилиндры и сферы.
• минимальные поверхности , которые определяются тем свойством, что их средняя кривизна равна нулю в каждой точке. Наиболее известными примерами являются катеноиды и геликоиды , хотя было обнаружено гораздо больше. Минимальные поверхности также могут определяться свойствами, связанными с площадью поверхности , в результате чего они обеспечивают математическую модель формы мыльных пленок при натяжении на проволочный каркас.
• линейчатые поверхности , которые представляют собой поверхности, через каждую точку которых проходит хотя бы одна прямая линия; примеры включают цилиндр и гиперболоид одного листа.

Удивительный результат Карла Фридриха Гаусса , известный как теорема эгрегиума , показал, что гауссова кривизна поверхности, которая по определению связана с тем, как кривые на поверхности меняют направление в трехмерном пространстве, на самом деле может быть измерена длинами кривых, лежащих на поверхностях, вместе с углами, образующимися при пересечении двух кривых на поверхности. Терминологически это говорит о том, что гауссову кривизну можно вычислить по первой фундаментальной форме (также называемой метрическим тензором ) поверхности. Вторая фундаментальная форма , напротив, представляет собой объект, который кодирует, как длины и углы кривых на поверхности искажаются, когда кривые отталкиваются от поверхности.

Несмотря на измерение различных аспектов длины и угла, первая и вторая фундаментальные формы не являются независимыми друг от друга и удовлетворяют определенным ограничениям, называемым уравнениями Гаусса-Кодацци . Основная теорема, часто называемая фундаментальной теоремой дифференциальной геометрии поверхностей, утверждает, что всякий раз, когда два объекта удовлетворяют ограничениям Гаусса-Кодацци, они возникают как первая и вторая фундаментальные формы регулярной поверхности.

Используя первую фундаментальную форму, можно определять новые объекты на регулярной поверхности. Геодезические — это кривые на поверхности, удовлетворяющие некоторому обыкновенному дифференциальному уравнению второго порядка , которое задается первой фундаментальной формой. Они самым непосредственным образом связаны с изучением длин кривых; геодезическая достаточно короткой длины всегда будет кривой кратчайшей длины на поверхности, соединяющей две ее концы. Таким образом, геодезические имеют фундаментальное значение для задачи оптимизации определения кратчайшего пути между двумя заданными точками на регулярной поверхности.

Можно также определить параллельный транспорт вдоль любой заданной кривой, что дает рецепт, как деформировать касательный вектор к поверхности в одной точке кривой до касательных векторов во всех других точках кривой. Рецепт определяется обыкновенным дифференциальным уравнением первого порядка , которое задается первой фундаментальной формой.

Все вышеперечисленные концепции, по сути, связаны с исчислением многих переменных. Теорема Гаусса-Бонне — более глобальный результат, который связывает гауссову кривизну поверхности с ее топологическим типом. Он утверждает, что среднее значение гауссовой кривизны полностью определяется эйлеровой характеристикой поверхности вместе с ее площадью поверхности.

Понятия риманова многообразия и римановой поверхности являются двумя обобщениями регулярных поверхностей, обсуждавшихся выше. В частности, по существу вся обсуждаемая здесь теория регулярных поверхностей имеет обобщение в теории римановых многообразий. Это не относится к римановым поверхностям, хотя каждая регулярная поверхность является примером римановой поверхности.

Регулярные поверхности в евклидовом пространстве

Определение

Интуитивно понятно, что сфера гладкая, а конус или пирамида в силу вершины или рёбер — нет. Понятие «регулярная поверхность» является формализацией понятия гладкой поверхности. В определении используется локальное представление поверхности посредством отображений между евклидовыми пространствами . Для таких карт существует стандартное понятие гладкости; отображение между двумя открытыми подмножествами евклидова пространства является гладким, если его частные производные любого порядка существуют в каждой точке области.

Ниже приведены три эквивалентных способа представления определения; среднее определение, пожалуй, наиболее визуально интуитивно понятно, поскольку оно, по сути, говорит, что регулярная поверхность является подмножеством ℝ ³ который локально является графиком гладкой функции (будь то область в плоскости yz , плоскости xz или плоскости xy ).

Локальная параметризация формы пятна Монжа для верхней полусферы 2-сферы, полученная проецированием на xy . плоскость

Объекты, используемые в определении	Регулярная поверхность в евклидовом пространстве ℝ 3 является подмножеством S из ℝ 3 такая, что каждая точка S имеет...
Локальная параметризация	... открытая окрестность U ⊂ S , для которой существует открытое подмножество V в ℝ 2 и гомеоморфизм f : V → U такой, что f , как функция V → ℝ 3 , бесконечно дифференцируемо (т.е. гладко) для каждой точки V две частные производные ∂ u f и ∂ v f как линейно независимы элементы ℝ 3 .
Патчи Монжа	... открытая окрестность U ⊂ ℝ 3 для которого существует открытое подмножество V из ℝ 2 и гладкая функция h : V → ℝ такая, что выполняется одно из следующих условий: S ∩  U = {( h ( u , v ), u , v ) : ( u , v ) ∈ V } S ∩  U = {( u , h ( u , v ), v ) : ( u , v ) ∈ V } S ∩  U = {( u , v , h ( u , v )) : ( u , v ) ∈ V }.
Неявные функции	... открытая окрестность U ⊂ ℝ 3 для которой существует гладкая функция F : U → ℝ с: S ∩ U знак равно {( Икс , y , z ) ∈ U : F ( Икс , y , z ) знак равно 0 } в каждой точке S ∩ U хотя бы одна частная производная F не равна нулю.

Гомеоморфизмы, входящие в первое определение, известны как локальные параметризации , локальные системы координат или локальные карты на S . Эквивалентность первых двух определений утверждает, что вокруг любой точки на регулярной поверхности всегда существуют локальные параметризации вида ( u , v ) ↦ ( h ( u , v ), u , v ) , ( u , v ) ↦ ( ты , час ( ты , v ), v ) , или ( ты , v ) ↦ ( ты , v , час ( ты , v )) , известные как патчи Монжа . Функции F , как и в третьем определении, называются локальными определяющими функциями . Эквивалентность всех трех определений следует из теоремы о неявной функции .

Изменения координат между различными местными картами должны быть плавными.

Для любых двух локальных параметризаций f : V → U и f ′ : V ′ → U ′ регулярной поверхности композиция f ⁻¹ ∘ f ′ обязательно гладко как отображение между открытыми подмножествами ℝ ² . Это показывает, что любая регулярная поверхность естественным образом имеет структуру гладкого многообразия , причем гладкий атлас задается обратными локальными параметризациями.

В классической теории дифференциальной геометрии поверхности обычно изучаются только в регулярном случае. Однако также часто изучаются нерегулярные поверхности, в которых две частные производные ∂ _u f и ∂ _v f локальной параметризации могут не быть линейно независимыми . В этом случае S может иметь особенности, такие как ребра возврата . Такие поверхности обычно изучаются в теории особенностей . Другие ослабленные формы регулярных поверхностей встречаются в компьютерном проектировании , когда поверхность разбивается на непересекающиеся части, при этом производные локальных параметризаций не могут быть даже непрерывными вдоль границ.

Гиперболоид из двух листов

Тор

Геликоид

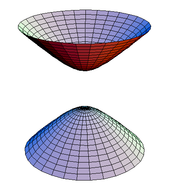
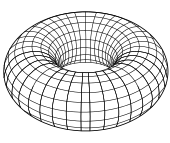
Простые примеры. Простым примером регулярной поверхности является 2-сфера {( x , y , z ) | Икс ² + и ² + я ² = 1 }; эту поверхность можно покрыть шестью пятнами Монжа (по два каждого из трех типов, приведенных выше), приняв h ( u , v ) = ± (1 − u ² − v ² ) ^1/2 . Его также можно охватить двумя локальными параметризациями с использованием стереографической проекции . Набор {( x , y , z ) : (( x ² + и ² ) ^1/2 - р ) ² + я ² "=" р ² — тор вращения радиусов r и R. } Это обычная поверхность; локальные параметризации могут быть заданы в виде

$f(s,t)={\big (}(R\cos s+r)\cos t,(R\cos s+r)\sin t,R\sin s{\big )}.$

Гиперболоид на двух листах {( x , y , z ) : z ² = 1 + х ² + и ² } — регулярная поверхность; его можно покрыть двумя патчами Монжа с h ( u , v ) = ±(1 + u ² + v ² ) ^1/2 . Геликоид появляется в теории минимальных поверхностей . Он покрывается единственной локальной параметризацией: f ( u , v ) = ( u sin v , u cos v , v ) .

Касательные векторы и нормальные векторы

См. Также: Параметрическая поверхность § Касательная плоскость и вектор нормали.

Дополнительная информация: Тангенциальные и нормальные компоненты.

Пусть S — регулярная поверхность в ℝ ³ , и пусть p будет элементом S . Используя любое из приведенных выше определений, можно выделить определенные векторы в ℝ ³ как касательная к S в точке p , и некоторые векторы в ℝ ³ как ортогональный S в точке p .

Объекты, используемые в определении	Вектор X в ℝ 3 касается S в точке p , если...	Вектор n в ℝ 3 нормально к S в точке p , если...
Локальная параметризация	... при любой локальной параметризации f : V → S с p ∈ f ( V ) , X является линейной комбинацией $\textstyle {\frac {\partial f}{\partial u}}{\big |}_{f^{-1}(p)}$ и $\textstyle {\frac {\partial f}{\partial v}}{\big |}_{f^{-1}(p)}$	... он ортогонален каждому касательному вектору к S в точке p
Патчи Монжа	... для любого патча Монжа ( u , v ) ↦ ( u , v , h ( u , v ) , диапазон которого включает p , имеем $X^{1}{\frac {\partial h}{\partial u}}+X^{2}{\frac {\partial h}{\partial v}}-X^{3}=0,$ с частными производными, оцененными в точке ( p 1 , p 2 ) . Аналогичное определение применимо и к пятнам Монжа двух других форм.	... для любого патча Монжа ( u , v ) ↦ ( u , v , h ( u , v ) , диапазон которого включает p , n кратно ( ∂ h / ∂ u , ∂ час / ∂ v , −1) по оценке в точке ( п 1 , п 2 ) . Аналогичное определение применимо и к пятнам Монжа двух других форм.
Неявные функции	... для любой локальной определяющей функции F , область определения которой содержит p , X ортогонально ∇ F ( p )	... для любой локальной определяющей функции F, область определения которой содержит p , n кратно ∇ F ( p )

Видно, что касательное пространство или касательная плоскость к S в точке p , которая определяется как состоящая из всех касательных векторов к S в точке p , является двумерным линейным подпространством ℝ ³ ; его часто обозначают T _p S . Нормальное пространство к S в точке p , которое определяется как состоящее из всех нормальных векторов к S в точке p , является одномерным линейным подпространством ℝ ³ которое ортогонально касательному пространству T _p S . Таким образом, в каждой точке p из S существует два нормальных вектора единичной длины (единичные нормальные векторы). Единичные нормальные векторы в точке p могут быть заданы через локальные параметризации, патчи Монжа или локальные определяющие функции по формулам

$\pm \left.{\frac {{\frac {\partial f}{\partial u}}\times {\frac {\partial f}{\partial v}}}{{\big \|}{\frac {\partial f}{\partial u}}\times {\frac {\partial f}{\partial v}}{\big \|}}}\right|_{f^{-1}(p)},\qquad \pm \left.{\frac {{\big (}{\frac {\partial h}{\partial u}},{\frac {\partial h}{\partial v}},-1{\big )}}{\sqrt {1+{\big (}{\frac {\partial h}{\partial u}}{\big )}^{2}+{\big (}{\frac {\partial h}{\partial v}}{\big )}^{2}}}}\right|_{(p_{1},p_{2})},\qquad {\text{or}}\qquad \pm {\frac {\nabla F(p)}{{\big \|}\nabla F(p){\big \|}}},$

следуя тем же обозначениям, что и в предыдущих определениях.

Полезно также отметить «внутреннее» определение касательных векторов, типичное для обобщения теории регулярных поверхностей на случай гладких многообразий . Он определяет касательное пространство как абстрактное двумерное вещественное векторное пространство, а не как линейное подпространство ℝ. ³ . В этом определении говорится, что касательный вектор к S в точке p является присвоением каждой локальной параметризации f : V → S с p ∈ f ( V ) двух чисел X ¹ и Х ² , такой, что для любой другой локальной параметризации f ′ : V → S с p ∈ f ( V ) (и с соответствующими числами ( X ′) ¹ и ( Х ′) ² ), надо

${\begin{pmatrix}X^{1}\\X^{2}\end{pmatrix}}=A_{f'(p)}{\begin{pmatrix}(X')^{1}\\(X')^{2}\end{pmatrix}},$

где A _{f ′( p )} — матрица Якоби отображения f ⁻¹ ∘ f ′ , оцененный в точке f ′( p ) . Набор касательных векторов к S в точке p естественно имеет структуру двумерного векторного пространства. Касательный вектор в этом смысле соответствует касательному вектору в предыдущем смысле, если рассматривать вектор

$X^{1}{\frac {\partial f}{\partial u}}+X^{2}{\frac {\partial f}{\partial v}}.$

в ℝ ³ . Условие Якобиана на X ¹ и Х ² гарантирует, по цепному правилу , что этот вектор не зависит от f .

Для гладких функций на поверхности векторные поля (т.е. касательные векторные поля) имеют важную интерпретацию как операторы или дифференцирования первого порядка. Позволять $S$ быть регулярной поверхностью, $U$ открытое подмножество плоскости и $f:U\rightarrow S$координатная карта. Если $V=f(U)$, космос $C^{\infty }(U)$ можно отождествить с $C^{\infty }(V)$. Сходным образом $f$ идентифицирует векторные поля на $U$ с включенными векторными полями $V$. Принимая стандартные переменные u и v , векторное поле имеет вид $X=a\partial _{u}+b\partial _{v}$, с гладкими функциями a и b . Если $X$ является векторным полем и $g$ — гладкая функция, то $Xg$также является гладкой функцией. Дифференциальный оператор первого порядка $X$ является выводом , т. е. удовлетворяет правилу Лейбница $X(gh)=(Xg)h+g(Xh).$

Для векторных полей X и Y несложно проверить, что оператор $[X,Y]=XY-YX$является выводом, соответствующим векторному полю. Она называется скобкой Лия. $[X,Y]$. Он кососимметричный $[X,Y]=-[Y,X]$ и удовлетворяет тождеству Якоби:

$[[X,Y],Z]+[[Y,Z],X]+[[Z,X],Y]=0.$

Таким образом, векторные поля на $U$ или $V$ образуют алгебру Ли под скобкой Ли.

, оператор формы и

Пусть S — регулярная поверхность в ℝ ³ . Учитывая локальную параметризацию f : V → S и единичное нормальное векторное поле n к f ( V ) , можно определить следующие объекты как вещественнозначные или матричные функции на V . Первая фундаментальная форма зависит только от f , а не от n . В четвертом столбце записано, как эти функции зависят от f , путем связи функций E ', F ', G ', L ' и т.д., возникающих при другом выборе локальной параметризации, f ': V ' → S , к возникающим для f . Здесь A обозначает матрицу Якоби функции f ^–1 ∘ ж ′ . Тогда ключевое соотношение при установлении формул четвертого столбца будет

${\begin{pmatrix}{\frac {\partial f'}{\partial u}}\\{\frac {\partial f'}{\partial v}}\end{pmatrix}}=A{\begin{pmatrix}{\frac {\partial f}{\partial u}}\\{\frac {\partial f}{\partial v}}\end{pmatrix}},$

как следует из правила цепочки .

Терминология	Обозначения	Определение	Зависимость от локальной параметризации
Первая фундаментальная форма	И	$E={\frac {\partial f}{\partial u}}\cdot {\frac {\partial f}{\partial u}}$	${\begin{pmatrix}E'&F'\\F'&G'\end{pmatrix}}=A{\begin{pmatrix}E&F\\F&G\end{pmatrix}}A^{T}$
	Ф	$F={\frac {\partial f}{\partial u}}\cdot {\frac {\partial f}{\partial v}}$
	г	$G={\frac {\partial f}{\partial v}}\cdot {\frac {\partial f}{\partial v}}$
Вторая фундаментальная форма	л	$L={\frac {\partial ^{2}f}{\partial u^{2}}}\cdot n$	${\begin{pmatrix}L'&M'\\M'&N'\end{pmatrix}}=A{\begin{pmatrix}L&M\\M&N\end{pmatrix}}A^{T}$
	М	$M={\frac {\partial ^{2}f}{\partial u\partial v}}\cdot n$
	Н	$N={\frac {\partial ^{2}f}{\partial v^{2}}}\cdot n$
Оператор формы	п	$P={\begin{pmatrix}L&M\\M&N\end{pmatrix}}{\begin{pmatrix}E&F\\F&G\end{pmatrix}}^{-1}$	$P'=APA^{-1}$
Гауссова кривизна	К	$K={\frac {LN-M^{2}}{EG-F^{2}}}$	$K'=K$
Средняя кривизна	ЧАС	$H={\frac {GL-2FM+EN}{2(EG-F^{2})}}$	$H'=H$
Главные кривизны	$\kappa _{\pm }$	$H\pm {\sqrt {H^{2}-K}}$	$\kappa _{\pm }'=\kappa _{\pm }$

Непосредственным вычислением с матрицей, определяющей оператор формы, можно проверить, что гауссова кривизна является определителем оператора формы, средняя кривизна составляет половину следа оператора формы, а главные кривизны являются собственными значениями оператора формы. оператор формы; более того, гауссова кривизна является произведением главных кривизн, а средняя кривизна является их суммой. Эти наблюдения также можно сформулировать как определения этих объектов. Эти наблюдения также ясно показывают, что последние три строки четвертого столбца следуют непосредственно из предыдущей строки, поскольку аналогичные матрицы имеют одинаковый определитель, след и собственные значения. Очень важно отметить E , G и EG − F ² все обязательно положительные. Это гарантирует, что матрица, обратная в определении оператора формы, четко определена и что главные кривизны являются действительными числами.

Обратите также внимание, что отрицание выбора единичного нормального векторного поля приведет к отрицанию второй фундаментальной формы, оператора формы, средней кривизны и главных кривизн, но оставит гауссову кривизну неизменной. Таким образом, это показало, что при наличии регулярной поверхности S гауссову кривизну S можно рассматривать как вещественную функцию на S ; относительно выбора единичного нормального векторного поля на всем S две главные кривизны и средняя кривизна также являются вещественными функциями на S .

Определение второй фундаментальной формы

Главные кривизны в точке поверхности

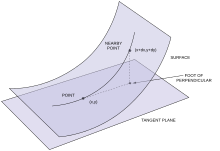
Геометрически первую и вторую фундаментальные формы можно рассматривать как дающие информацию о том, как f ( u , v ) движется в ℝ ³ поскольку ( u , v ) перемещается в V . В частности, первая фундаментальная форма кодирует скорость движения f , а вторая фундаментальная форма кодирует степень, в которой его движение происходит в направлении вектора нормали n . Другими словами, вторая фундаментальная форма в точке p кодирует длину ортогональной проекции от S к касательной плоскости к S в точке p ; в частности, он дает квадратичную функцию, которая лучше всего аппроксимирует эту длину. Это мышление можно уточнить с помощью формул

${\begin{aligned}\lim _{(h,k)\to (0,0)}{\frac {{\big |}f(u+h,v+k)-f(u,v){\big |}^{2}-{\big (}Eh^{2}+2Fhk+Gk^{2}{\big )}}{h^{2}+k^{2}}}&=0\\\lim _{(h,k)\to (0,0)}{\frac {{\big (}f(u+h,v+k)-f(u,v){\big )}\cdot n-{\frac {1}{2}}{\big (}Lh^{2}+2Mhk+Nk^{2}{\big )}}{h^{2}+k^{2}}}&=0,\end{aligned}}$

как следует непосредственно из определений фундаментальных форм и теоремы Тейлора в двух измерениях. Главные кривизны можно рассматривать следующим образом. В данной точке p из S рассмотрим совокупность всех плоскостей, содержащих линию, ортогональную S. к Каждая такая плоскость имеет кривую пересечения с S , которую можно рассматривать как плоскую кривую внутри самой плоскости. Две основные кривизны в точке p представляют собой максимальное и минимальное возможные значения кривизны этой плоской кривой в точке p , поскольку рассматриваемая плоскость вращается вокруг нормальной линии.

Следующее суммирует расчет вышеуказанных величин относительно патча Монжа f ( u , v ) = ( u , v , h ( u , v ) ) . Здесь h _u и h _v обозначают две частные производные h с аналогичными обозначениями для вторых частных производных. Вторая фундаментальная форма и все последующие величины вычисляются относительно заданного выбора единичного нормального векторного поля.

Количество	Формула
Поле единичного нормального вектора	$n={\frac {(-h_{u},-h_{v},1)}{\sqrt {1+h_{u}^{2}+h_{v}^{2}}}}$
Первая фундаментальная форма	${\begin{pmatrix}E&F\\F&G\end{pmatrix}}={\begin{pmatrix}1+h_{u}^{2}&h_{u}h_{v}\\h_{u}h_{v}&1+h_{v}^{2}\end{pmatrix}}$
Вторая фундаментальная форма	${\begin{pmatrix}L&M\\M&N\end{pmatrix}}={\frac {1}{\sqrt {1+h_{u}^{2}+h_{v}^{2}}}}{\begin{pmatrix}h_{uu}&h_{uv}\\h_{uv}&h_{vv}\end{pmatrix}}$
Оператор формы	$P={\frac {1}{(1+h_{u}^{2}+h_{v}^{2})^{3/2}}}{\begin{pmatrix}h_{uu}(1+h_{v}^{2})-h_{uv}h_{u}h_{v}&h_{uv}(1+h_{u}^{2})-h_{uu}h_{u}h_{v}\\h_{uv}(1+h_{v}^{2})-h_{vv}h_{u}h_{v}&h_{vv}(1+h_{u}^{2})-h_{uv}h_{u}h_{v}\end{pmatrix}}$
Гауссова кривизна	$K={\frac {h_{uu}h_{vv}-h_{uv}^{2}}{(1+h_{u}^{2}+h_{v}^{2})^{2}}}$
Средняя кривизна	$H={\frac {(1+h_{v}^{2})h_{uu}-2h_{u}h_{v}h_{uv}+(1+h_{u}^{2})h_{vv}}{2(1+h_{u}^{2}+h_{v}^{2})^{3/2}}}$

Эгрегиума.

Пусть S — регулярная поверхность в ℝ ³ . Символы Кристоффеля присваивают каждой локальной параметризации f : V → S восемь функций на V , определяемых формулой

${\begin{pmatrix}\Gamma _{11}^{1}&\Gamma _{12}^{1}&\Gamma _{21}^{1}&\Gamma _{22}^{1}\\\Gamma _{11}^{2}&\Gamma _{12}^{2}&\Gamma _{21}^{2}&\Gamma _{22}^{2}\end{pmatrix}}={\begin{pmatrix}E&F\\F&G\end{pmatrix}}^{-1}{\begin{pmatrix}{\frac {1}{2}}{\frac {\partial E}{\partial u}}&{\frac {1}{2}}{\frac {\partial E}{\partial v}}&{\frac {1}{2}}{\frac {\partial E}{\partial v}}&{\frac {\partial F}{\partial v}}-{\frac {1}{2}}{\frac {\partial G}{\partial u}}\\{\frac {\partial F}{\partial u}}-{\frac {1}{2}}{\frac {\partial E}{\partial v}}&{\frac {1}{2}}{\frac {\partial G}{\partial u}}&{\frac {1}{2}}{\frac {\partial G}{\partial u}}&{\frac {1}{2}}{\frac {\partial G}{\partial v}}\end{pmatrix}}.$

Их также можно определить по следующим формулам, в которых n — единичное нормальное векторное поле вдоль f ( V ) , а L , M , N — соответствующие компоненты второй фундаментальной формы:

${\begin{aligned}{\frac {\partial ^{2}f}{\partial u^{2}}}&=\Gamma _{11}^{1}{\frac {\partial f}{\partial u}}+\Gamma _{11}^{2}{\frac {\partial f}{\partial v}}+Ln\\{\frac {\partial ^{2}f}{\partial u\partial v}}&=\Gamma _{12}^{1}{\frac {\partial f}{\partial u}}+\Gamma _{12}^{2}{\frac {\partial f}{\partial v}}+Mn\\{\frac {\partial ^{2}f}{\partial v^{2}}}&=\Gamma _{22}^{1}{\frac {\partial f}{\partial u}}+\Gamma _{22}^{2}{\frac {\partial f}{\partial v}}+Nn.\end{aligned}}$

Ключом к этому определению является то, что ∂ f / ∂ u , ∂ f / ∂ v и n образуют основу ℝ ³ в каждой точке, относительно которой каждое из трех уравнений однозначно определяет символы Кристоффеля как координаты вторых частных производных f . Выбор единичной нормали не влияет на символы Кристоффеля, поскольку если n заменить на его отрицание, то компоненты второй фундаментальной формы также инвертируются, и поэтому знаки Ln , Mn , Nn остаются неизменными.

Второе определение показывает, в контексте локальной параметризации, что символы Кристоффеля геометрически естественны. Хотя формулы в первом определении кажутся менее естественными, они важны, поскольку показывают, что символы Кристоффеля можно вычислить из первой фундаментальной формы, что не сразу становится очевидным из второго определения. подставив непосредственно первое определение во второе и воспользовавшись определениями E , F , G. Эквивалентность определений можно проверить ,

утверждают Уравнения Кодацци , что

${\begin{aligned}{\frac {\partial L}{\partial v}}-{\frac {\partial M}{\partial u}}&=L\Gamma _{12}^{1}+M(\Gamma _{12}^{2}-\Gamma _{11}^{1})-N\Gamma _{11}^{2}\\{\frac {\partial M}{\partial v}}-{\frac {\partial N}{\partial u}}&=L\Gamma _{22}^{1}+M(\Gamma _{22}^{2}-\Gamma _{12}^{1})-N\Gamma _{12}^{2}.\end{aligned}}$

Эти уравнения могут быть непосредственно получены из второго определения символов Кристоффеля, данного выше; например, первое уравнение Кодацци получается путем дифференцирования первого уравнения по v , второго уравнения по u , вычитания этих двух и взятия скалярного произведения с n . Уравнение Гаусса утверждает, что

${\begin{aligned}KE&={\frac {\partial \Gamma _{11}^{2}}{\partial v}}-{\frac {\partial \Gamma _{21}^{2}}{\partial u}}+\Gamma _{21}^{2}\Gamma _{11}^{1}+\Gamma _{22}^{2}\Gamma _{11}^{2}-\Gamma _{11}^{2}\Gamma _{21}^{1}-\Gamma _{12}^{2}\Gamma _{21}^{2}\\KF&={\frac {\partial \Gamma _{12}^{2}}{\partial v}}-{\frac {\partial \Gamma _{22}^{2}}{\partial u}}+\Gamma _{21}^{2}\Gamma _{12}^{1}-\Gamma _{11}^{2}\Gamma _{22}^{1}\\KG&={\frac {\partial \Gamma _{22}^{1}}{\partial u}}-{\frac {\partial \Gamma _{12}^{1}}{\partial v}}+\Gamma _{11}^{1}\Gamma _{22}^{1}+\Gamma _{12}^{1}\Gamma _{22}^{2}-\Gamma _{21}^{1}\Gamma _{12}^{1}-\Gamma _{22}^{1}\Gamma _{12}^{2}\end{aligned}}$

Их можно вывести аналогично уравнениям Кодацци, причем одно из них использует уравнения Вайнгартена вместо скалярного произведения с n . Хотя они записаны как три отдельных уравнения, они идентичны, когда в них подставляются определения символов Кристоффеля в терминах первой фундаментальной формы. Есть много способов записать полученное выражение, один из них был получен в 1852 году Бриоски . используя умелое использование определителей:

$K={\frac {1}{(EG-F^{2})^{2}}}\det {\begin{pmatrix}-{1 \over 2}{\frac {\partial ^{2}E}{\partial v^{2}}}+{\frac {\partial ^{2}F}{\partial u\partial v}}-{1 \over 2}{\frac {\partial ^{2}G}{\partial u^{2}}}&{1 \over 2}{\frac {\partial E}{\partial u}}&{\frac {\partial F}{\partial u}}-{1 \over 2}{\frac {\partial E}{\partial v}}\\{\frac {\partial F}{\partial v}}-{1 \over 2}{\frac {\partial G}{\partial u}}&E&F\\{1 \over 2}{\frac {\partial G}{\partial v}}&F&G\end{pmatrix}}-{\frac {1}{(EG-F^{2})^{2}}}\det {\begin{pmatrix}0&{1 \over 2}{\frac {\partial E}{\partial v}}&{1 \over 2}{\frac {\partial G}{\partial u}}\\{1 \over 2}{\frac {\partial E}{\partial v}}&E&F\\{1 \over 2}{\frac {\partial G}{\partial u}}&F&G\end{pmatrix}}.$

Когда считается, что символы Кристоффеля определяются первой фундаментальной формой, уравнения Гаусса и Кодацци представляют собой определенные ограничения между первой и второй фундаментальными формами. Уравнение Гаусса заслуживает особого внимания, поскольку оно показывает, что гауссова кривизна может быть вычислена непосредственно из первой фундаментальной формы, без необходимости использования какой-либо другой информации; то же самое означает, что LN − M ² фактически может быть записано как функция E , F , G , хотя отдельные компоненты L , M , N не могут. Это известно как теорема эгрегиума и было главным открытием Карла Фридриха Гаусса . Это особенно поразительно, если вспомнить геометрическое определение гауссовой кривизны S , определяемой максимальным и минимальным радиусами соприкасающихся окружностей; кажется, что они фундаментально определяются геометрией того, как S изгибается внутри ℝ ³ . Тем не менее, теорема показывает, что их произведение можно определить из «внутренней» геометрии S , имея дело только с длинами кривых вдоль S и углами, образующимися при их пересечении. Как сказал Марсель Бергер :

Эта теорема сбивает с толку. [...] Это та теорема, которая могла бы подождать еще десятки лет, прежде чем ее откроет другой математик, поскольку, в отличие от большей части интеллектуальной истории, она абсолютно не висела в воздухе. [...] Насколько нам известно, сегодня не существует простого геометрического доказательства теоремы egregium.

Уравнения Гаусса-Кодацци также можно кратко выразить и вывести на языке форм связи , принадлежащем Эли Картану . На языке тензорного исчисления , используя естественные метрики и связи на тензорных расслоениях , уравнение Гаусса можно записать как H ² − | ч | ² = R , а два уравнения Кодацци можно записать как ∇ ₁ h ₁₂ = ∇ ₂ h ₁₁ и ∇ ₁ h ₂₂ = ∇ ₂ h ₁₂ ; сложные выражения, связанные с символами Кристоффеля и первой фундаментальной формой, полностью поглощены определениями ковариантной тензорной производной ∇ h и скалярной кривизны R . Пьер Бонне доказал, что две квадратичные формы, удовлетворяющие уравнениям Гаусса-Кодацци, всегда однозначно локально определяют вложенную поверхность. По этой причине уравнения Гаусса-Кодацци часто называют фундаментальными уравнениями для вложенных поверхностей, точно определяя, откуда берутся внутренние и внешние кривизны. Они допускают обобщения на поверхности, вложенные в более общие римановы многообразия .

Изометрии

Диффеоморфизм $\varphi$ между открытыми сетами $U$ и $V$ на обычной поверхности $S$ называется изометрией, если она сохраняет метрику, т. е. первую фундаментальную форму. Таким образом, для каждой точки $p$ в $U$ и касательные векторы $w_{1},\,\,w_{2}$ в $p$, имеются равенства

$E(p)w_{1}\cdot w_{1}+2F(p)w_{1}\cdot w_{2}+G(p)w_{2}\cdot w_{2}=E(\varphi (p))\varphi ^{\prime }(w_{1})\cdot \varphi ^{\prime }(w_{1})+2F(\varphi (p))\varphi ^{\prime }(w_{1})\cdot \varphi ^{\prime }(w_{2})+G(\varphi (p))\varphi ^{\prime }(w_{1})\cdot \varphi ^{\prime }(w_{2}).$

С точки зрения внутреннего продукта, исходящего из первой фундаментальной формы, это можно переписать как

$(w_{1},w_{2})_{p}=(\varphi ^{\prime }(w_{1}),\varphi ^{\prime }(w_{2}))_{\varphi (p)}$.

Катеноид – правильная поверхность вращения.

С другой стороны, длина параметризованной кривой $\gamma (t)=(x(t),y(t))$ можно рассчитать как

$L(\gamma )=\int _{a}^{b}{\sqrt {E{\dot {x}}\cdot {\dot {x}}+2F{\dot {x}}\cdot {\dot {y}}+G{\dot {y}}\cdot {\dot {y}}}}\,dt$

и, если кривая лежит в $U$, правила замены переменных показывают, что

$L(\varphi \circ \gamma )=L(\gamma ).$

И наоборот, если $\varphi$ сохраняет длины всех параметризованных кривых, тогда $\varphi$является изометрией. Действительно, для подходящего выбора $\gamma$, касательные векторы ${\dot {x}}$ и ${\dot {y}}$ дать произвольные касательные векторы $w_{1}$ и $w_{2}$. Равенства должны выполняться для любого выбора касательных векторов $w_{1}$ и $w_{2}$ а также $\varphi ^{\prime }(w_{1})$ и $\varphi ^{\prime }(w_{2})$, так что $(\varphi ^{\prime }(w_{1}),\varphi ^{\prime }(w_{2}))_{\varphi (p)}=(w_{1},w_{1})_{p}$.

Простой пример изометрии представлен двумя параметризациями. $f_{1}$ и $f_{2}$ открытого набора $U$ на обычные поверхности $S_{1}$ и $S_{2}$. Если $E_{1}=E_{2}$, $F_{1}=F_{2}$ и $G_{1}=G_{2}$, затем $\varphi =f_{2}\circ f_{1}^{-1}$ представляет собой изометрию $f_{1}(U)$ на $f_{2}(U)$.

Цилиндр и плоскость дают примеры поверхностей, которые являются локально изометрическими, но которые не могут быть продолжены до изометрии по топологическим причинам. Другой пример: катеноид и геликоид локально изометричны.

Ковариантные производные

Основные статьи: Ковариантная производная и риманова связность на поверхности

Касательное векторное поле X на S сопоставляет каждому p в S касательный вектор X _p к S в точке p . Согласно «внутреннему» определению касательных векторов, данному выше, касательное векторное поле X затем присваивает каждой локальной параметризации f : V → S две действительные функции X ¹ и Х ² на V , так что

$X_{p}=X^{1}{\big (}f^{-1}(p){\big )}{\frac {\partial f}{\partial u}}{\Big |}_{f^{-1}(p)}+X^{2}{\big (}f^{-1}(p){\big )}{\frac {\partial f}{\partial v}}{\Big |}_{f^{-1}(p)}$

для каждого p в S . Говорят, что X гладко, если функции X ¹ и Х ² гладкие для любого выбора f . Согласно другим определениям касательных векторов, данным выше, касательное векторное поле X на S можно также рассматривать как отображение X : S → ℝ. ³ такой, что X ( p ) содержится в касательном пространстве T _p S ⊂ ℝ ³ для каждого p в S . Как это часто бывает в более общей ситуации с гладкими многообразиями , касательные векторные поля также можно определить как некоторые дифференциальные операторы в пространстве гладких функций S. на

Ковариантные производные (также называемые «тангенциальными производными») Туллио Леви-Чивита и Грегорио Риччи-Курбастро предоставляют средства дифференцирования гладких тангенциальных векторных полей. Учитывая касательное векторное поле X и касательный вектор Y к S в точке p , ковариантная производная ∇ _Y X представляет собой некоторый касательный вектор к S в точке p . Следовательно, если X и Y оба являются касательными векторными полями, то ∇ _Y X также можно рассматривать как касательное векторное поле; итеративно, если X , Y и Z являются тангенциальными векторными полями, можно вычислить ∇ _Z ∇ _Y X , которое будет другим тангенциальным векторным полем. Есть несколько способов определить ковариантную производную; первый ниже использует символы Кристоффеля и «внутреннее» определение касательных векторов, а второй является более явно геометрическим.

Учитывая касательное векторное поле X и касательный вектор Y к S в точке p , можно определить ∇ _Y X как касательный вектор к p , который присваивает локальной параметризации f : V → S два числа

$(\nabla _{Y}X)^{k}=D_{(Y^{1},Y^{2})}X^{k}{\Big |}_{f^{-1}(p)}+\sum _{i=1}^{2}\sum _{j=1}^{2}{\big (}\Gamma _{ij}^{k}X^{j}{\big )}{\Big |}_{f^{-1}(p)}Y^{i},\qquad (k=1,2)$

где Д _{( Y ¹ , И ² )} — производная по направлению . Это часто сокращается до менее громоздкой формы (∇ _Y X ). ^к = ∂ _Y ( Икс ^к ) + Ю ^я С ^к
_ij X ^дж , используя обозначения Эйнштейна и неявно понимая места вычисления функции. Это соответствует стандартному рецепту римановой геометрии для получения связности из римановой метрики . Фундаментальным фактом является то, что вектор

$(\nabla _{Y}X)^{1}{\frac {\partial f}{\partial u}}+(\nabla _{Y}X)^{2}{\frac {\partial f}{\partial v}}$

в ℝ ³ не зависит от выбора локальной параметризации f , хотя проверять это довольно утомительно.

Можно также определить ковариантную производную с помощью следующего геометрического подхода, который не использует символы Кристоффеля или локальные параметризации. Пусть X — векторное поле на S , рассматриваемое как функция S → ℝ ³ . Учитывая любую кривую c : ( a , b ) → S , можно рассмотреть композицию X ∘ c : ( a , b ) → ℝ ³ . Как карту между евклидовыми пространствами, ее можно дифференцировать по любому входному значению, чтобы получить элемент ( X ∘ c )′( t ) из ℝ ³ . Ортогональная проекция этого вектора на T _{c ( t )} S определяет ковариантную производную ∇ _{c ′( t )} X . Хотя это очень геометрически чистое определение, необходимо показать, что результат зависит только от c '( t ) и X , а не от c и X ; Для этого небольшого технического аргумента можно использовать локальную параметризацию.

Из второго определения не сразу видно, что ковариантное дифференцирование зависит только от первой фундаментальной формы S ; однако это следует из первого определения, поскольку символы Кристоффеля могут быть определены непосредственно из первой фундаментальной формы. Несложно проверить, что эти два определения эквивалентны. Ключевым моментом является то, что когда мы рассматриваем X ¹ ∂ f / ∂ u + X ² ∂ f / ∂ v как ℝ ³ -значная функция, ее дифференцирование вдоль кривой приводит к вторым частным производным ∂ ² ж ; символы Кристоффеля входят с ортогональной проекцией в касательное пространство из-за формулировки символов Кристоффеля как тангенциальных компонентов вторых производных f относительно базиса. ∂ f / ∂ u , ∂ ж / ∂ v , п . Это обсуждается в разделе выше.

Правую часть трех уравнений Гаусса можно выразить с помощью ковариантного дифференцирования. Например, правая часть

${\frac {\partial \Gamma _{11}^{2}}{\partial v}}-{\frac {\partial \Gamma _{21}^{2}}{\partial u}}+\Gamma _{21}^{2}\Gamma _{11}^{1}+\Gamma _{22}^{2}\Gamma _{11}^{2}-\Gamma _{11}^{2}\Gamma _{21}^{1}-\Gamma _{12}^{2}\Gamma _{21}^{2}$

можно признать второй координатой

$\nabla _{\frac {\partial f}{\partial v}}\nabla _{\frac {\partial f}{\partial u}}{\frac {\partial f}{\partial u}}-\nabla _{\frac {\partial f}{\partial u}}\nabla _{\frac {\partial f}{\partial v}}{\frac {\partial f}{\partial u}}$

относительно основы ∂ f / ∂ u , ∂ f / ∂ v , в чем можно непосредственно убедиться, используя определение ковариантного дифференцирования с помощью символов Кристоффеля. На языке римановой геометрии это наблюдение можно также сформулировать так: правые части уравнений Гаусса представляют собой различные компоненты кривизны Риччи связи Леви -Чивита первой фундаментальной формы, когда они интерпретируются как риманова метрика. .

Примеры

Поверхность вращения, полученная вращением кривой x = 2 + cos z вокруг оси z .

Поверхности революции

Дополнительная информация: Поверхность революции.

Поверхность вращения получается вращением кривой в плоскости xz вокруг оси z . К таким поверхностям относятся сферы, цилиндры, конусы, торы и катеноид . Общие эллипсоиды , гиперболоиды и параболоиды таковыми не являются. Предположим, что кривая параметризована

$x=c_{1}(s),\,\,z=c_{2}(s)$

с s , взятым из интервала ( a , b ) . Если c ₁ никогда не равен нулю, если c ₁ ′ и c ₂ ′ никогда оба не равны нулю и если c ₁ и c ₂ оба гладкие, то соответствующая поверхность вращения

$S={\Big \{}{\big (}c_{1}(s)\cos t,c_{1}(s)\sin t,c_{2}(s){\big )}\colon s\in (a,b){\text{ and }}t\in \mathbb {R} {\Big \}}$

будет обычной поверхностью в ℝ ³ . Локальная параметризация f : ( a , b ) × (0, 2π) → S определяется выражением

$f(s,t)={\big (}c_{1}(s)\cos t,c_{1}(s)\sin t,c_{2}(s){\big )}.$

По отношению к этой параметризации геометрические данные:

Количество	Формула
Поле единичного нормального вектора	$n={\frac {{\big (}-c_{2}'(s)\cos t,-c_{2}'(s)\sin t,c_{1}'(s){\big )}}{\sqrt {c_{1}'(s)^{2}+c_{2}'(s)^{2}}}}$
Первая фундаментальная форма	${\begin{pmatrix}E&F\\F&G\end{pmatrix}}={\begin{pmatrix}c_{1}'(s)^{2}+c_{2}'(s)^{2}&0\\0&c_{1}(s)^{2}\end{pmatrix}}$
Вторая фундаментальная форма	${\begin{pmatrix}L&M\\M&N\end{pmatrix}}={\begin{pmatrix}{\frac {c_{1}'(s)c_{2}''(s)-c_{2}'(s)c_{1}''(s)}{\sqrt {c_{1}'(s)^{2}+c_{2}'(s)^{2}}}}&0\\0&{\frac {c_{1}(s)c_{2}'(s)}{\sqrt {c_{1}'(s)^{2}+c_{2}'(s)^{2}}}}\end{pmatrix}}$
Главные кривизны	${\frac {c_{1}'(s)c_{2}''(s)-c_{2}'(s)c_{1}''(s)}{{\big (}c_{1}'(s)^{2}+c_{2}'(s)^{2}{\big )}^{3/2}}}\quad {\text{and}}\quad {\frac {c_{2}'(s)}{c_{1}(s){\sqrt {c_{1}'(s)^{2}+c_{2}'(s)^{2}}}}}$
Гауссова кривизна	$K={\frac {c_{2}'(s){\big (}c_{1}'(s)c_{2}''(s)-c_{2}'(s)c_{1}''(s){\big )}}{c_{1}(s){\big (}c_{1}'(s)^{2}+c_{2}'(s)^{2}{\big )}^{2}}}$
Средняя кривизна	$H={\frac {1}{2}}{\frac {c_{1}'(s)c_{2}''(s)-c_{2}'(s)c_{1}''(s)}{{\big (}c_{1}'(s)^{2}+c_{2}'(s)^{2}{\big )}^{3/2}}}+{\frac {1}{2}}{\frac {c_{2}'(s)}{c_{1}(s){\sqrt {c_{1}'(s)^{2}+c_{2}'(s)^{2}}}}}.$

В особом случае, когда исходная кривая параметризована длиной дуги, т.е. ( c ₁ ′( s )) ² + ( c ₂ ′( s )) ² = 1 , можно дифференцировать, чтобы найти c ₁ ′( s ) c ₁ "( s ) + c ₂ ′( s ) c ₂ "( s ) = 0 . При подстановке в гауссову кривизну имеем упрощенную формулу

$K=-{\frac {c_{1}''(s)}{c_{1}(s)}}\qquad {\text{and}}\qquad H=c_{1}'(s)c_{2}''(s)-c_{2}'(s)c_{1}''(s)+{\frac {c_{2}'(s)}{c_{1}(s)}}.$

Простота этой формулы позволяет особенно легко изучать класс вращательно-симметричных поверхностей с постоянной гауссовой кривизной. Сводя его к альтернативному случаю, когда c ₂ (s) = s , можно изучать вращательно-симметричные минимальные поверхности, в результате чего любая такая поверхность является частью плоскости или масштабированного катеноида.

Каждую кривую постоянной t на S можно параметризовать как геодезическую; кривая постоянной s на S может быть параметризована как геодезическая тогда и только тогда, когда c ₁ ′(s) равно нулю. Обычно геодезические на S подчиняются соотношению Клеро .

Квадратный эллипсоид

Квадрикические поверхности

Дополнительная информация: Квадрикическая поверхность.

Рассмотрим квадричную поверхность, определяемую формулой

${x^{2} \over a}+{y^{2} \over b}+{z^{2} \over c}=1.$

Эта поверхность допускает параметризацию

$x={\sqrt {a(a-u)(a-v) \over (a-b)(a-c)}},\,\,y={\sqrt {b(b-u)(b-v) \over (b-a)(b-c)}},\,\,z={\sqrt {c(c-u)(c-v) \over (c-b)(c-a)}}.$

Гауссова кривизна и средняя кривизна определяются выражениями

$K={abc \over u^{2}v^{2}},\,\,K_{m}=-(u+v){\sqrt {abc \over u^{3}v^{3}}}.$

Однополостный квадратичный гиперболоид , который является линейчатой ​​поверхностью двумя разными способами.

Линейчатые поверхности

Дополнительная информация: Линейчатая поверхность.

Линейчатая поверхность — это поверхность, которая может быть образована движением прямой в E. ³ . Выбрав направляющую на поверхности, то есть гладкую кривую единичной скорости c ( t ), ортогональную прямым линиям, а затем выбрав u ( t ) в качестве единичных векторов вдоль кривой в направлении линий, вектор скорости v = c _ты и ты удовлетворяешь

$u\cdot v=0,\,\,\|u\|=1,\,\,\|v\|=1.$

Поверхность состоит из точек

$c(t)+s\cdot u(t)$

поскольку s и t меняются.

Тогда, если

$a=\|u_{t}\|,\,\,b=u_{t}\cdot v,\,\,\alpha =-{\frac {b}{a^{2}}},\,\,\beta ={\frac {\sqrt {a^{2}-b^{2}}}{a^{2}}},$

Гауссова и средняя кривизна определяются выражениями

$K=-{\beta ^{2} \over ((s-\alpha )^{2}+\beta ^{2})^{2}},\,\,K_{m}=-{r[(s-\alpha )^{2}+\beta ^{2})]+\beta _{t}(s-\alpha )+\beta \alpha _{t} \over [(s-\alpha )^{2}+\beta ^{2}]^{\frac {3}{2}}}.$

Гауссова кривизна линейчатой ​​поверхности обращается в нуль тогда и только тогда, когда u _t и v пропорциональны: Это условие эквивалентно тому, что поверхность является огибающей плоскостей вдоль кривой, содержащих касательный вектор v и ортогональный вектор u , т. е. поверхность развертывается вдоль кривой. В более общем смысле поверхность в E ³ имеет исчезающую гауссову кривизну вблизи точки тогда и только тогда, когда она развертывается вблизи этой точки. (Эквивалентное условие приведено ниже в терминах метрики.)

Минимальные поверхности

Дополнительная информация: Минимальная поверхность.

В 1760 году Лагранж распространил результаты Эйлера по вариационному исчислению, включающие интегралы от одной переменной, на две переменные. Он имел в виду следующую проблему:

Учитывая замкнутую кривую в E ³ , найдите поверхность, имеющую кривую в качестве границы с минимальной площадью.

Такая поверхность называется минимальной поверхностью .

В 1776 году Жан Батист Мёнье показал, что дифференциальное уравнение, полученное Лагранжем, эквивалентно обращению в нуль средней кривизны поверхности:

Поверхность минимальна тогда и только тогда, когда ее средняя кривизна равна нулю.

Минимальные поверхности в реальной жизни интерпретируются просто: это форма, которую примет мыльная пленка, если проволочный каркас в форме кривой окунуть в мыльный раствор, а затем осторожно вынуть. Вопрос о том, существует ли минимальная поверхность с заданной границей, называется проблемой Плато в честь бельгийского физика Жозефа Плато , который проводил эксперименты с мыльными пленками в середине девятнадцатого века. В 1930 году Джесси Дуглас и Тибор Радо дали утвердительный ответ на проблему Плато (за эту работу Дуглас был награжден одной из первых медалей Филдса в 1936 году).

Многие явные примеры минимальной поверхности известны явно, такие как катеноид , геликоид , поверхность Шерка и поверхность Эннепера . В этой области были проведены обширные исследования, обобщенные Оссерманом (2002) . В частности, результат Оссермана показывает, что если минимальная поверхность неплоская, то ее образ при отображении Гаусса плотен в S ² .

Поверхности с (слева направо) постоянной отрицательной, нулевой и положительной гауссовой кривизной.

Поверхности

Эухенио Бельтрами (1835–1899)

Если поверхность имеет постоянную гауссову кривизну, ее называют поверхностью постоянной кривизны .

• Единичная сфера в E ³ имеет постоянную гауссову кривизну +1.
• Евклидова плоскость и цилиндр имеют постоянную гауссову кривизну 0.
• Поверхности вращения с φ _tt = φ имеют постоянную гауссову кривизну –1. Частные случаи получаются, если взять φ ( t ) = C ch t , C sinh t и C e ^т . Последний случай представляет собой классическую псевдосферу , созданную вращением трактрисы вокруг центральной оси. В 1868 году Эудженио Бельтрами показал, что геометрия псевдосферы напрямую связана с геометрией гиперболической плоскости , открытой независимо Лобачевским (1830) и Бояи (1832). Уже в 1840 г. ученик Гаусса Ф. Миндинг получил тригонометрические формулы для псевдосферы, идентичные формулам для гиперболической плоскости. Внутренняя геометрия этой поверхности теперь лучше понята в терминах метрики Пуанкаре на верхней полуплоскости или единичном круге и описывается другими моделями, такими как модель Клейна или модель гиперболоида , полученная при рассмотрении двухлистной модели. гиперболоид q ( x , y , z ) = −1 в трехмерном пространстве Минковского , где q ( x , y , z ) = x ² + и ² - С ² .

Каждая из этих поверхностей постоянной кривизны имеет транзитивную группу Ли симметрий. Этот теоретико-групповой факт имеет далеко идущие последствия, тем более примечательные, что эти специальные поверхности играют центральную роль в геометрии поверхностей, что обусловлено теоремой Пуанкаре об униформизации (см. ниже).

Другие примеры поверхностей с гауссовой кривизной 0 включают конусы , касательные развертывающиеся поверхности и, в более общем смысле, любую развертывающуюся поверхность.

Локальная метрическая структура

Дополнительная информация: Риманово многообразие.

Для любой поверхности, включенной в евклидово пространство размерности 3 или выше, можно измерить длину кривой на поверхности, угол между двумя кривыми и площадь области на поверхности. Эта структура бесконечно закодирована в римановой метрике на поверхности посредством линейных элементов и элементов площади . Классически в девятнадцатом и начале двадцатого веков только поверхности, встроенные в R ³ Рассматривались и метрика задавалась в виде положительно определенной матрицы размером 2×2 , плавно меняющейся от точки к точке при локальной параметризации поверхности. Идея локальной параметризации и изменения координат была позже формализована через нынешнее абстрактное понятие многообразия , топологического пространства, где гладкая структура задается локальными картами на многообразии, точно так же, как сегодня планета Земля отображается в атласах . Изменения координат между разными картами одного и того же региона должны быть плавными. Точно так же, как контурные линии на реальных картах кодируют изменения высоты, принимая во внимание локальные искажения поверхности Земли для расчета истинных расстояний, так и риманова метрика описывает расстояния и площади «в мелочах» на каждой локальной карте. В каждой локальной карте риманова метрика задается путем плавного присвоения каждой точке положительно определенной матрицы 2 × 2; при взятии другой карты матрица преобразуется в соответствии с матрицей Якоби изменения координат. Тогда многообразие имеет структуру двумерного Риманово многообразие .

Оператор формы

Вильгельм Бляшке (1885-1962)

Дифференциал . dn карты Гаусса n можно использовать для определения типа внешней кривизны, известного как оператор формы или карту Вайнгартена . Этот оператор впервые неявно появился в работе Вильгельма Бляшке , а затем явно в трактате Бурали-Форти и Бургати. Поскольку в каждой точке x поверхности касательное пространство является пространством внутреннего произведения , оператор формы S _x можно определить как линейный оператор в этом пространстве по формуле

$(S_{x}v,w)=(dn(v),w)$

для касательных векторов v , w (скалярное произведение имеет смысл, поскольку dn ( v ) и w оба лежат в E ³ ). Правая часть симметрична относительно v и w , поэтому оператор формы самосопряжен в касательном пространстве. Собственные значения S _x — это просто главные кривизны k ₁ и k ₂ в точке x . В частности, определителем оператора формы в точке является гауссова кривизна, но она содержит и другую информацию, поскольку средняя кривизна составляет половину следа оператора формы. Средняя кривизна является внешним инвариантом. Во внутренней геометрии цилиндр развертывается, а это означает, что каждая его часть по своей сути неотличима от части плоскости, поскольку его гауссова кривизна тождественно равна нулю. Однако его средняя кривизна не равна нулю; следовательно, внешне он отличается от плоскости.

оператор формы можно определить как линейный оператор в Sp _: → TpM _. касательных , TpM _{Эквивалентно} : пространствах Если n — единичное нормальное поле к M , а v — касательный вектор, то

$S(v)=\pm \nabla _{v}n$

(стандартного соглашения о том, использовать ли + или – в определении, не существует).

В общем, собственные векторы и собственные значения оператора формы в каждой точке определяют направления изгиба поверхности в каждой точке. Собственные значения соответствуют главным кривизнам поверхности, а собственные векторы — соответствующим главным направлениям. Главные направления определяют направления, в которых должна двигаться кривая, встроенная в поверхность, чтобы иметь максимальную и минимальную кривизну, причем они задаются главными кривизнами.

Геодезические кривые на поверхности

Кривые на поверхности, которые минимизируют длину между конечными точками, называются геодезическими ; это форма, которую приняла бы резинка, натянутая между двумя точками. Математически они описываются с помощью обыкновенных дифференциальных уравнений и вариационного исчисления . Дифференциальная геометрия поверхностей вращается вокруг изучения геодезических. До сих пор остается открытым вопрос, возникает ли каждая риманова метрика на двумерной локальной карте в результате вложения в трехмерное евклидово пространство: теория геодезических была использована, чтобы показать, что это верно в важном случае, когда компоненты метрики являются аналитическими .

Геодезика

Геодезический треугольник на сфере. Геодезические – это большие дуги окружностей.

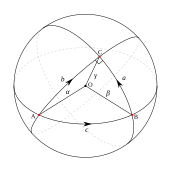
Учитывая кусочно-гладкий путь c ( t ) = ( x ( t ), y ( t )) в карте для t в [ a , b ] , его длина определяется выражением

$L(c)=\int _{a}^{b}(E{\dot {x}}^{2}+2F{\dot {x}}{\dot {y}}+G{\dot {y}}^{2})^{\frac {1}{2}}\,dt$

и энергия за счет

$E(c)=\int _{a}^{b}(E{\dot {x}}^{2}+2F{\dot {x}}{\dot {y}}+G{\dot {y}}^{2})\,dt.$

Длина не зависит от параметризации пути. Согласно уравнениям Эйлера-Лагранжа , если c ( t ) — путь, минимизирующий длину, параметризованный длиной дуги , он должен удовлетворять уравнениям Эйлера

${\ddot {x}}+\Gamma _{11}^{1}{\dot {x}}^{2}+2\Gamma _{12}^{1}{\dot {x}}{\dot {y}}+\Gamma _{22}^{1}{\dot {y}}^{2}=0$

${\ddot {y}}+\Gamma _{11}^{2}{\dot {x}}^{2}+2\Gamma _{12}^{2}{\dot {x}}{\dot {y}}+\Gamma _{22}^{2}{\dot {y}}^{2}=0$

где символы Кристоффеля Γ ^к
_ij имеют вид

$\Gamma _{ij}^{k}={\tfrac {1}{2}}g^{km}(\partial _{j}g_{im}+\partial _{i}g_{jm}-\partial _{m}g_{ij})$

где г ₁₁ = Е , г ₁₂ = F , г ₂₂ = G и г ^ij является обратной матрицей к g _ij . Путь, удовлетворяющий уравнениям Эйлера, называется геодезической . Согласно неравенству Коши – Шварца путь, минимизирующий энергию, представляет собой просто геодезическую, параметризованную длиной дуги; и для любой геодезической параметр t пропорционален длине дуги.

Геодезическая кривизна

См. Также: Геодезическая кривизна и система Дарбу.

Геодезическая кривизна k _g в точке кривой c ( t ) , параметризованной длиной дуги, на ориентированной поверхности определяется как

$k_{g}={\ddot {c}}(t)\cdot \mathbf {n} (t).$

где n ( t ) — «основная» единица измерения нормали к кривой на поверхности, построенная путем поворота единичного касательного вектора ċ ( t ) на угол +90 °.

• Геодезическая кривизна в точке является внутренним инвариантом, зависящим только от метрики вблизи точки.
• Кривая единичной скорости на поверхности является геодезической тогда и только тогда, когда ее геодезическая кривизна равна нулю во всех точках кривой.
• Кривая единичной скорости c ( t ) на вложенной поверхности является геодезической тогда и только тогда, когда ее вектор ускорения c ( t ) нормален к поверхности.

Геодезическая кривизна точно измеряет, насколько далека кривая на поверхности от геодезической.

Ортогональные координаты

Когда F = 0 на всей координатной карте, например, в геодезических полярных координатах, обсуждаемых ниже, изображения линий, параллельных x и y осям , ортогональны и обеспечивают ортогональные координаты . Если Ч = ( EG ) ^{1 ⁄ 2} , то гауссова кривизна определяется выражением

$K=-{1 \over 2H}\left[\partial _{x}\left({\frac {G_{x}}{H}}\right)+\partial _{y}\left({\frac {E_{y}}{H}}\right)\right].$

Если при этом E = 1 , так что H = G ^{1 ⁄ 2} , то угол φ на пересечении геодезической ( x ( t ), y ( t )) и прямой y = константа определяется уравнением

$\tan \varphi =H\cdot {\frac {\dot {y}}{\dot {x}}}.$

Производная φ задается классической формулой производной Гаусса:

${\dot {\varphi }}=-H_{x}\cdot {\dot {y}}.$

полярные

Карл Якоби (1804–1851)

Контурные линии, отслеживающие движение точек по фиксированной кривой, движущейся по геодезическим линиям к базовой точке.

Как только на поверхности задана метрика и зафиксирована базовая точка, существует уникальная геодезическая, соединяющая базовую точку с каждой достаточно близкой точкой. Направление геодезической в ​​базовой точке и расстояние однозначно определяют другую конечную точку. Эти два бита данных, направление и величина, таким образом, определяют касательный вектор в базовой точке. Карта касательных векторов к конечным точкам плавно охватывает окрестность базовой точки и определяет так называемую «экспоненциальную карту», ​​определяя карту локальных координат в этой базовой точке. Выметенная окрестность имеет свойства, аналогичные шарам в евклидовом пространстве, а именно: любые две точки в ней соединены единственной геодезической. Это свойство называется «геодезической выпуклостью», а координаты называются «нормальными координатами». Явное вычисление нормальных координат можно выполнить, рассматривая дифференциальное уравнение, которому удовлетворяют геодезические. Свойства выпуклости являются следствиями леммы Гаусса и ее обобщений. Грубо говоря, эта лемма гласит, что геодезические, начинающиеся в базовой точке, должны разрезать сферы фиксированного радиуса с центрами в базовой точке под прямым углом. Геодезические полярные координаты получаются путем объединения экспоненциальной карты с полярными координатами касательных векторов в базовой точке. Тогда гауссова кривизна поверхности определяется отклонением метрики второго порядка в точке от евклидовой метрики. В частности, гауссова кривизна является инвариантом метрики, знаменитой Гаусса. Теорема Эгрегиум . Удобный способ понять кривизну — это обыкновенное дифференциальное уравнение, сначала рассмотренное Гауссом, а затем обобщенное Якоби, возникающее в результате изменения нормальных координат вокруг двух разных точек. Уравнение Гаусса – Якоби обеспечивает другой способ вычисления гауссовой кривизны. Геометрически это объясняет, что происходит с геодезическими от фиксированной базовой точки, когда конечная точка изменяется вдоль небольшого сегмента кривой в зависимости от данных, записанных в поле Якоби , векторном поле вдоль геодезической. Спустя полтора века после Гаусса и Якоби Марстон Морс дал более концептуальную интерпретацию поля Якоби в терминах вторых производных энергетической функции на бесконечномерном гильбертовом многообразии путей.

Экспоненциальная карта

Дополнительная информация: Нормальные координаты.

Теория обыкновенных дифференциальных уравнений показывает, что если f ( t , v ) гладкое, то дифференциальное уравнение dv / dt = f ( t , v ) с начальным условием v (0) = v ₀ имеет единственное решение для | т | достаточно мало и решение плавно зависит от t и v ₀ . Это означает, что для достаточно малых касательных векторов v в данной точке p = ( x ₀ , y ₀ ) существует геодезическая c _v ( t ), определенная на (−2, 2) с c _v (0) = ( x ₀ , y ₀ ) и ċ _v (0) знак равно v . Более того, если | s | ≤ 1 , тогда c _sv знак равно c _v ( st ) . Экспоненциальное отображение определяется

exp _p ( v ) = c _v (1)

и дает диффеоморфизм между кругом ‖ v ‖ < δ и окрестностью точки p ; в более общем смысле отображение, отправляющее ( p , v ) в exp _p ( v ) , дает локальный диффеоморфизм на окрестность ( p , p ) . Экспоненциальная карта дает геодезические нормальные координаты вблизи p .

Вычисление нормальных координат

Существует стандартная методика (см., например, Berger (2004) ) для вычисления замены переменных на нормальные координаты u , v в точке как формальное разложение в ряд Тейлора . Если координаты x , y в точке (0,0) локально ортогональны, запишите

Икс ( ты , v ) знак равно αu + L ( ты , v ) + λ ( ты , v ) + …

y ( u , v ) = βv + M ( u , v ) + μ ( u , v ) + …

где L , M — квадратичные, а λ , µ — кубические однородные полиномы от u и v . Если u и v фиксированы, x ( t ) = x ( tu , tv ) и y ( t ) = y ( tu , tv ) можно рассматривать как формальные степенные решения уравнений Эйлера: это однозначно определяет α , β , L , M , λ и µ .

Лемма Гаусса

Основная статья: лемма Гаусса (риманова геометрия)

В геодезических полярных координатах геодезические, исходящие из начала координат, пересекают круги постоянного радиуса ортогонально. Расстояния вдоль радиусов являются истинными расстояниями, но на концентрических кругах маленькие дуги имеют длину H ( r , θ ) = G ( r , θ ) ^{1 ⁄ 2} раз больше угла, на который они опираются.

В этих координатах матрица g ( x ) удовлетворяет условию g (0) = I , а прямые t ↦ tv являются геодезическими, проходящим через 0. Из уравнений Эйлера следует матричное уравнение

g ( v ) v = v ,

ключевой результат, обычно называемый леммой Гаусса . Геометрически это утверждает, что

геодезические, проходящие через 0, разрезают круги с центром в 0 ортогонально .

Если взять полярные координаты ( r , θ ) , то метрика имеет вид

дс ² = доктор ² + г ( р , θ ) dθ ² .

В геодезических координатах легко проверить, что геодезические, проходящие через нуль, минимизируют длину. Тогда топология риманова многообразия задается функцией расстояния d ( p , q ) , а именно нижней границей длин кусочно-гладких путей между p и q . Это расстояние локально реализуется геодезическими, так что в нормальных координатах d (0, v ) = ‖ v ‖ . Если радиус δ взять достаточно малым, небольшое усиление леммы Гаусса показывает, что образ U диска ‖ v ‖ < δ при экспоненциальном отображении является геодезически выпуклым , т. е. любые две точки из U соединены единственной геодезической, лежащей полностью U. внутри

Великая Теорема

Основная статья: Теорема Эгрегиума

Гаусса Теорема Egregium , «Замечательная теорема», показывает, что гауссова кривизна поверхности может быть вычислена исключительно в терминах метрики и, таким образом, является внутренним инвариантом поверхности, независимым от любого изометрического вложения в E. ³ и не изменяется при преобразованиях координат. В частности, изометрии поверхностей сохраняют гауссову кривизну.

Эта теорема может быть выражена через разложение метрики в степенной ряд, ds , задается в нормальных координатах ( u , v ) как

дс ² = от ² + дв ² - K ( ты дв – v ду ) ² /12 + … .

Уравнение Гаусса–Якоби

Дополнительная информация: Поле Якоби.

Изменение координат с нормальных координат в точке p на нормальные координаты в соседней точке q дает уравнение Штурма – Лиувилля , удовлетворяемое формулой H ( r , θ ) = G ( r , θ ) ^{1 ⁄ 2} , открытая Гауссом и позже Якоби обобщенная ,

H рр = – KH

Якобиан точке этой замены координат в q равен H _r . Это дает еще один способ установить внутреннюю природу гауссовой кривизны. Поскольку H ( r , θ ) можно интерпретировать как длину элемента линии в направлении θ , уравнение Гаусса-Якоби показывает, что гауссова кривизна измеряет распространение геодезических линий на геометрической поверхности по мере их удаления от точки.

Оператор Лапласа-Бельтрами

На поверхности с локальной метрикой

$ds^{2}=E\,dx^{2}+2F\,dx\,dy+G\,dy^{2}$

и оператор Лапласа–Бельтрами

$\Delta f={1 \over H}\left(\partial _{x}{G \over H}\partial _{x}f-\partial _{x}{F \over H}\partial _{y}f-\partial _{y}{F \over H}\partial _{x}f+\partial _{y}{E \over H}\partial _{y}f\right),$

где Н ² = ЭГ − F ² , гауссова кривизна в точке определяется формулой

$K=-3\lim _{r\rightarrow 0}\Delta (\log r),$

где r обозначает геодезическое расстояние от точки.

В изотермических координатах , впервые рассмотренных Гауссом, метрика должна иметь специальный вид

$ds^{2}=e^{\varphi }(dx^{2}+dy^{2}).\,$

В этом случае оператор Лапласа–Бельтрами имеет вид

$\Delta =e^{-\varphi }\left({\frac {\partial ^{2}}{\partial x^{2}}}+{\frac {\partial ^{2}}{\partial y^{2}}}\right)$

и φ удовлетворяет уравнению Лиувилля

$\Delta \varphi =-2K.\,$

Известно, что изотермические координаты существуют в окрестности любой точки поверхности, хотя все доказательства на сегодняшний день опираются на нетривиальные результаты для уравнений в частных производных . Существует элементарное доказательство для минимальных поверхностей.

Теорема Гаусса–Бонне

Основная статья: теорема Гаусса – Бонне

Триангуляция тора

На сфере или гиперболоиде площадь геодезического треугольника , т. е. треугольника, все стороны которого являются геодезическими, пропорциональна разности суммы внутренних углов и π . Константа пропорциональности — это не что иное, как гауссова кривизна, константа для этих поверхностей. Для тора разница равна нулю, что отражает тот факт, что его гауссова кривизна равна нулю. Это стандартные результаты по сферической, гиперболической и школьной тригонометрии (см. ниже). Гаусс обобщил эти результаты на произвольную поверхность, показав, что интеграл гауссовой кривизны по внутренней части геодезического треугольника также равен этой разнице углов или избытку. Его формула показала, что гауссова кривизна может быть рассчитана вблизи точки как предел площади превышения угла для геодезических треугольников, сжимающихся к точке. Поскольку любую замкнутую поверхность можно разложить на геодезические треугольники, формулу также можно использовать для вычисления интеграла кривизны по всей поверхности. Как частный случай того, что сейчас называют Теорема Гаусса-Бонне , Гаусс доказал, что этот интеграл всегда был в 2π раза больше целого числа, топологический инвариант поверхности, называемый эйлеровой характеристикой . Этот инвариант легко вычислить комбинаторно, исходя из количества вершин, ребер и граней треугольников в разложении, также называемом триангуляцией . Это взаимодействие между анализом и топологией было предшественником многих более поздних результатов в геометрии, кульминацией которых стала теорема об индексе Атьи-Зингера . В частности, свойства кривизны накладывают ограничения на топологию поверхности.

Геодезические треугольники

Гаусс доказал, что если ∆ — геодезический треугольник на поверхности с углами α , β и γ в вершинах A , B и C , то

$\int _{\Delta }K\,dA=\alpha +\beta +\gamma -\pi .$

Фактически, взяв геодезические полярные координаты с началом координат A и AB , AC - радиусы под полярными углами 0 и α :

${\begin{aligned}\int _{\Delta }K\,dA&=\int _{\Delta }KH\,dr\,d\theta =-\int _{0}^{\alpha }\int _{0}^{r_{\theta }}\!H_{rr}\,dr\,d\theta \\&=\int _{0}^{\alpha }1-H_{r}(r_{\theta },\theta )\,d\theta =\int _{0}^{\alpha }d\theta +\int _{\pi -\beta }^{\gamma }\!\!d\varphi \\&=\alpha +\beta +\gamma -\pi ,\end{aligned}}$

где второе равенство следует из уравнения Гаусса–Якоби, а четвертое — из формулы производной Гаусса в ортогональных координатах ( r , θ ) .

Формула Гаусса показывает, что кривизну в точке можно рассчитать как предел превышения угла α + β + γ - π над площадью для последовательно меньших геодезических треугольников вблизи точки. Качественно поверхность является положительно или отрицательно искривленной в зависимости от знака избытка угла для сколь угодно малых геодезических треугольников.

Теорема Гаусса–Бонне

Эйлерова характеристика сферы, триангулированной как икосаэдр , равна V − E + F = 12 − 30 + 20 = 2 .

Основная статья: теорема Гаусса – Бонне

Поскольку каждое компактное ориентированное 2-многообразие M можно триангулировать малыми геодезическими треугольниками, отсюда следует, что

$\int _{M}KdA=2\pi \,\chi (M)$

где χ ( M ) обозначает эйлерову характеристику поверхности.

Фактически, если имеется F граней, E ребер и V вершин, то 3 F = 2 E и левая часть равна 2π V – π F = 2π( V – E + F ) = 2π χ ( M ) .

Это знаменитая теорема Гаусса-Бонне : она показывает, что интеграл гауссовой кривизны является топологическим инвариантом многообразия, а именно эйлеровой характеристикой. Эту теорему можно интерпретировать по-разному; возможно, одним из самых далеко идущих является теорема об индексе для эллиптического дифференциального оператора на M , один из простейших случаев теоремы Атьи-Зингера об индексе . Другой родственный результат, который можно доказать с помощью теоремы Гаусса – Бонне, - это теорема Пуанкаре-Хопфа об индексе для векторных полей на M , которые обращаются в нуль только в конечном числе точек: сумма индексов в этих точках равна эйлеровой характеристике, где индекс точки определяется следующим образом: на маленьком круге вокруг каждого изолированного нуля векторное поле определяет отображение в единичный круг; индекс — это просто номер витка этой карты.)

Кривизна и вложения

Если гауссова кривизна поверхности M всюду положительна, то эйлерова характеристика положительна, поэтому M гомеоморфна (и, следовательно, диффеоморфна) S. ² . Если дополнительно поверхность изометрически вложена в E ³ , отображение Гаусса обеспечивает явный диффеоморфизм. Как заметил Адамар , в этом случае поверхность выпуклая ; этот критерий выпуклости можно рассматривать как двумерное обобщение известного критерия второй производной выпуклости плоских кривых. Гильберт доказал, что каждая изометрически вложенная замкнутая поверхность должна иметь точку положительной кривизны. Таким образом, замкнутое риманово 2-многообразие неположительной кривизны никогда не может быть изометрически вложено в E ³ ; однако, как Адриано Гарсия показал с помощью уравнения Бельтрами для квазиконформных отображений , это всегда возможно для некоторой конформно эквивалентной метрики.

Поверхности постоянной кривизны

Односвязные поверхности постоянной кривизны 0, +1 и –1 представляют собой евклидову плоскость, единичную сферу в E ³ , и гиперболическая плоскость . Каждый из них имеет транзитивную трехмерную группу Ли , сохраняющих ориентацию изометрий G , которую можно использовать для изучения их геометрии. Каждую из двух некомпактных поверхностей можно отождествить с фактором G / K где K — максимальная компактная подгруппа группы G. , Здесь K изоморфен SO(2) . Любое другое замкнутое риманово 2-многообразие M постоянной гауссовой кривизны после масштабирования метрики в постоянный множитель, если необходимо, будет иметь одну из этих трех поверхностей в качестве универсального накрывающего пространства . В ориентируемом случае фундаментальная группа Γ группы M может быть отождествлена ​​с без кручения равномерной подгруппой в G , а M затем может быть отождествлена ​​с двойным смежным пространством Γ \ G / K . В случае сферы и евклидовой плоскости единственными возможными примерами являются сама сфера и торы, полученные как факторы R ² дискретными подгруппами ранга 2. Для замкнутых поверхностей рода g ≥ 2 римановых пространство модулей поверхностей, полученное при изменении Γ по всем таким подгруппам, имеет действительную размерность 6 g − 6 . Пуанкаре По теореме об униформизации любое ориентируемое замкнутое 2-многообразие конформно эквивалентно поверхности постоянной кривизны 0, +1 или –1. положительный масштабный коэффициент, можно заставить гауссову кривизну принимать ровно одно из этих значений (знак эйлеровой характеристики M Другими словами, умножив метрику на ).

Евклидова геометрия

Треугольник в плоскости

В случае евклидовой плоскости группа симметрии — это евклидова группа движения , полупрямое произведение двумерная группа трансляций по группе вращений. Геодезические представляют собой прямые линии, а геометрия закодирована в элементарных формулах тригонометрии , таких как правило косинусов для треугольника со сторонами a , b , c и углами α , β , γ :

$c^{2}=a^{2}+b^{2}-2ab\,\cos \gamma .$

Плоские торы можно получить, взяв фактор R ² решеткой в , т.е. свободной абелевой подгруппой ранга 2. Эти замкнутые поверхности не имеют изометрических вложений E ³ . Тем не менее они допускают изометрические вложения в E ⁴ ; в простейшем случае это следует из того, что тор является произведением двух окружностей и каждая окружность изометрически вкладывается в E ² .

Сферическая геометрия

Основные статьи: сферическая геометрия и сферическая тригонометрия.

Сферический треугольник

Площадь сферического треугольника на единичной сфере равна α + β + γ − π .

Группа изометрий единичной сферы S ² в Е ³ — ортогональная группа O(3) с группой вращения SO(3) в качестве подгруппы изометрий, сохраняющих ориентацию. Это прямой продукт SO(3) с антиподальным отображением , отправляющим x в – x . Группа SO(3) действует транзитивно на S ² . единичного Подгруппу стабилизатора вектора (0,0,1) можно отождествить с SO(2) , так что S ² = ТАК(3)/ТАК(2) .

Геодезические между двумя точками сферы представляют собой дуги большого круга с заданными конечными точками. Если точки не антиподальны, между ними существует единственная кратчайшая геодезическая. Геодезические также можно описать группово теоретически: каждая геодезическая, проходящая через Северный полюс (0,0,1), представляет собой орбиту подгруппы вращений вокруг оси, проходящей через противоположные точки на экваторе.

Сферический треугольник — это геодезический треугольник на сфере. Он определяется точками A , B , C на сфере со сторонами BC , CA , AB , образованными дугами большого круга длиной меньше π . Если длины сторон равны a , b , c , а углы между сторонами α , β , γ , то закон сферического косинуса гласит, что

$\cos c=\cos a\,\cos b+\sin a\,\sin b\,\cos \gamma .$

Площадь треугольника определяется выражением

Площадь знак равно α + β + γ - π .

Используя стереографическую проекцию с Северного полюса, сферу можно отождествить с расширенной комплексной плоскостью C ∪ {∞} . Явное отображение имеет вид

$\pi (x,y,z)={x+iy \over 1-z}\equiv u+iv.$

При этом соответствии каждое вращение S ² соответствует преобразованию Мёбиуса в SU(2) , единственному с точностью до знака. По отношению к координатам ( u , v ) в комплексной плоскости сферическая метрика становится

$ds^{2}={4(du^{2}+dv^{2}) \over (1+u^{2}+v^{2})^{2}}.$

Единичная сфера – это единственная замкнутая ориентируемая поверхность с постоянной кривизной +1. Фактор SO(3)/O(2) можно отождествить с вещественной проективной плоскостью . Он неориентируем и может быть описан как фактор S ² по антиподальному отображению (умножение на −1). Сфера односвязна, а вещественная проективная плоскость имеет фундаментальную группу Z ₂ . Конечные подгруппы SO(3) , соответствующие конечным подгруппам O(2) и группам симметрии платоновых тел , не действуют свободно на S ² , поэтому соответствующие факторы не являются 2-многообразиями, а просто орбифолдами .

Гиперболическая геометрия

Смотрите также: гиперболический треугольник и гиперболическая геометрия.

Анри Пуанкаре (1854–1912)

Неевклидова геометрия впервые обсуждался в письмах Гаусса, который на рубеже девятнадцатого века сделал обширные вычисления, которые, хотя и распространялись в частном порядке, он решил не публиковать. В 1830 году Лобачевский и независимо в 1832 году Боляи , сын одного из корреспондентов Гаусса, опубликовали синтетические версии этой новой геометрии, за что подверглись резкой критике. Однако только в 1868 году Бельтрами, а затем Кляйн в 1871 году и Пуанкаре в 1882 году дали конкретные аналитические модели того, что Кляйн назвал гиперболической геометрией . Появились четыре модели двумерной гиперболической геометрии:

• модель Бельтрами -Клейна ;
• Пуанкаре диск ;
• Пуанкаре верхняя полуплоскость ;
• гиперболоидная модель Вильгельма Киллинга в трехмерном пространстве Минковского .

Преимущество первой модели, основанной на диске, состоит в том, что геодезические на самом деле представляют собой отрезки линий (то есть пересечения евклидовых линий с открытым единичным диском). Последняя модель имеет то преимущество, что она дает конструкцию, полностью параллельную конструкции единичной сферы в трехмерном евклидовом пространстве. Однако из-за их применения в комплексном анализе и геометрии модели Пуанкаре получили наиболее широкое распространение: они взаимозаменяемы благодаря преобразованиям Мёбиуса между диском и верхней полуплоскостью.

Позволять

$D=\{z\,\colon |z|<1\}$

— диск Пуанкаре на комплексной плоскости с метрикой Пуанкаре

$ds^{2}={4(dx^{2}+dy^{2}) \over (1-x^{2}-y^{2})^{2}}.$

В полярных координатах ( r , θ ) метрика определяется выражением

$ds^{2}={4(dr^{2}+r^{2}\,d\theta ^{2}) \over (1-r^{2})^{2}}.$

Длина кривой γ :[ a , b ] → D определяется формулой

$\ell (\gamma )=\int _{a}^{b}{2|\gamma ^{\prime }(t)|\,dt \over 1-|\gamma (t)|^{2}}.$

Группа G = SU(1,1), заданная формулой

$G=\left\{{\begin{pmatrix}\alpha &\beta \\{\overline {\beta }}&{\overline {\alpha }}\end{pmatrix}}:\alpha ,\beta \in \mathbf {C} ,\,|\alpha |^{2}-|\beta |^{2}=1\right\}$

действует транзитивно преобразованиями Мёбиуса на D , а подгруппа стабилизатора 0 является группой вращения

$K=\left\{{\begin{pmatrix}\zeta &0\\0&{\overline {\zeta }}\end{pmatrix}}:\zeta \in \mathbf {C} ,\,|\zeta |=1\right\}.$

Факторгруппа SU(1,1)/± I — это группа изометрий D , сохраняющих ориентацию . Любые две точки z , w в D соединены уникальной геодезической, заданной частью круга или прямой линией, проходящей через точки z и w и ортогональной граничному кругу. Расстояние между z и w определяется выражением

$d(z,w)=2\tanh ^{-1}{\frac {|z-w|}{|1-{\overline {w}}z|}}.$

В частности d (0, r ) = 2 tanh ⁻¹ р и c ( т ) знак равно 1/2 дуги . tanh t — геодезическая, проходящая через 0 вдоль действительной оси, параметризованная длиной

Топология, определяемая этой метрикой, эквивалентна обычной евклидовой топологии, хотя как метрическое пространство ( D , d ) является полным.

Гиперболический треугольник в модели диска Пуанкаре

Гиперболический треугольник для этой метрики является геодезическим треугольником: любые три точки в D являются вершинами гиперболического треугольника. Если стороны имеют длину a , b , c с соответствующими углами α , β , γ , то правило гиперболического косинуса гласит, что

$\cosh c=\cosh a\,\cosh b-\sinh a\,\sinh b\,\cos \gamma .$

Площадь гиперболического треугольника определяется выражением

Площадь = π – a – b – c .

Единичный диск и верхняя полуплоскость

$H=\{w=x+iy\,\colon \,y>0\}$

конформно эквивалентны преобразованиями Мёбиуса

$w=i{1+z \over 1-z},\,\,z={w-i \over w+i}.$

При этом соответствии действие SL(2,R) преобразованиями Мёбиуса на H соответствует действию SU(1,1) на D . Метрика на H становится

$ds^{2}={dx^{2}+dy^{2} \over y^{2}}.$

Поскольку линии или окружности сохраняются при преобразованиях Мёбиуса, геодезические снова описываются прямыми или окружностями, ортогональными действительной оси.

Единичный круг с метрикой Пуанкаре представляет собой единственное односвязное ориентированное двумерное риманово многообразие постоянной кривизны −1. Любая ориентированная замкнутая поверхность M с этим свойством имеет D в качестве универсального накрывающего пространства. Его фундаментальную группу можно отождествить с компактной подгруппой без кручения Γ в SU(1,1) таким образом, что

$M=\Gamma \backslash G/K.$

В этом случае Г — конечно определенная группа . Генераторы и отношения кодируются в геодезически выпуклом фундаментальном геодезическом многоугольнике в D (или H геометрически соответствующем замкнутым геодезическим на M. ) ,

Примеры .

• поверхность Больца рода 2;
• квартика Клейна рода 3;
• рода поверхность Макбита 7;
• Первая тройка Гурвица рода 14.

Униформизация

Смотрите также: Теорема униформизации

Учитывая ориентированную замкнутую поверхность M с гауссовой кривизной K , метрику на M можно конформно изменить, масштабируя ее в е раз. ^{2 и} . Тогда новая гауссова кривизна K' определяется выражением

$K^{\prime }(x)=e^{-2u}(K(x)-\Delta u),$

где ∆ — лапласиан исходной метрики. Таким образом, чтобы показать, что данная поверхность конформно эквивалентна метрике постоянной кривизны K', достаточно решить следующий вариант уравнения Лиувилля :

$\Delta u=K^{\prime }e^{2u}+K(x).$

Когда M имеет эйлерову характеристику 0, то он диффеоморфен тору , K ′ = 0 , поэтому это сводится к решению

$\Delta u=K(x).$

Согласно стандартной эллиптической теории это возможно, поскольку интеграл от K по M равен нулю по теореме Гаусса – Бонне.

Когда M имеет отрицательную эйлерову характеристику, K' = −1 , поэтому уравнение, которое необходимо решить, имеет вид:

$\Delta u=-e^{2u}+K(x).$

Используя непрерывность экспоненциального отображения в пространстве Соболева, предложенную Нилом Трудингером , это нелинейное уравнение всегда можно решить.

Наконец, в случае 2-сферы K′ = 1 , и уравнение принимает вид:

$\Delta u=e^{2u}+K(x).$

До сих пор это нелинейное уравнение не анализировалось напрямую, хотя классические результаты, такие как теорема Римана-Роха, предполагают, что оно всегда имеет решение. Метод потока Риччи , разработанный Ричардом С. Гамильтоном , дает еще одно доказательство существования, основанное на нелинейных уравнениях в частных производных для доказательства существования. Фактически поток Риччи на конформных метриках на S ² определяется на функциях u ( x , t ) выражением

$u_{t}=4\pi -K'(x,t)=4\pi -e^{-2u}(K(x)-\Delta u).$

По истечении конечного времени Чоу показал, что K' становится положительным; Затем предыдущие результаты Гамильтона можно было бы использовать, чтобы показать, что K ' сходится к +1. До этих результатов о потоке Риччи Осгуд, Филлипс и Сарнак (1988) предложили альтернативный и технически более простой подход к униформизации, основанный на потоке на римановой метрике g, определяемой log det Δ _g .

Доказательство с использованием эллиптических операторов, открытое в 1988 году, можно найти в Ding (2001) . Пусть G — функция Грина на S ² удовлетворяющее Δ G = 1 + 4π δ _P , где δ _P — точечная мера в фиксированной точке P из S ² . Уравнение ∆ v = 2 K – 2 имеет гладкое решение v , поскольку правая часть имеет интеграл 0 по теореме Гаусса – Бонне. Таким образом, φ = 2 G + v удовлетворяет условию ∆ φ = 2 K на расстоянии от P . Отсюда следует, что g ₁ = e ^Фи g — полная метрика постоянной кривизны 0 в дополнении к P , которая, следовательно, изометрична плоскости. Комбинируя стереографическую проекцию , следует, что существует гладкая функция u такая, что e ^{2 и} g имеет гауссову кривизну +1 в дополнении к P . Функция u автоматически продолжается до гладкой функции на всем S ² .

связь и

Основная статья: Риманова связь на поверхности

Туллио Леви-Чивита (1873–1941)

Классический подход Гаусса к дифференциальной геометрии поверхностей был стандартным элементарным подходом. которое предшествовало появлению концепций риманова многообразия , инициированных Бернхардом Риманом в середине девятнадцатого века, и концепции связи , разработанной Туллио Леви-Чивитой , Эли Картаном и Германом Вейлем в начале двадцатого века. Понятие связи, ковариантной производной и параллельного переноса дало более концептуальный и единый способ понимания кривизны, который не только позволил делать обобщения на многообразия более высоких размерностей, но также предоставил важный инструмент для определения новых геометрических инвариантов, называемых характеристическими классами . Подход с использованием ковариантных производных и связей в настоящее время принят в более продвинутых учебниках.

Ковариантная производная

Соединения на поверхности можно определять с различных эквивалентных, но одинаково важных точек зрения. Риманова связь или связь Леви-Чивита . возможно, легче всего понять в терминах поднятия векторных полей первого порядка, , рассматриваемых как дифференциальные операторы действующие на функции на многообразии, до дифференциальных операторов на касательном расслоении или расслоении фреймов . В случае вложенной поверхности подъем до оператора векторных полей, называемый ковариантной производной , очень просто описывается в терминах ортогонального проектирования. Действительно, векторное поле на поверхности, вложенной в R ³ можно рассматривать как функцию от поверхности в R ³ . Другое векторное поле покомпонентно действует как дифференциальный оператор. Результирующее векторное поле не будет касаться поверхности, но это можно исправить, проецируя его ортогональную проекцию на касательное пространство в каждой точке поверхности. Как Риччи и Леви-Чивита поняли на рубеже двадцатого века, этот процесс зависит только от метрики и может быть локально выражен в терминах символов Кристоффеля.

Параллельный перенос вектора вокруг геодезического треугольника на сфере. Длина переносимого вектора и угол, образуемый им с каждой стороной, остаются постоянными.

Параллельный транспорт

Параллельный перенос касательных векторов вдоль кривой поверхности стал следующим крупным достижением в этой области, благодаря Леви-Чивите . Оно связано с более ранним понятием ковариантной производной, поскольку представляет собой монодромию обыкновенного дифференциального уравнения на кривой, определяемой ковариантной производной по отношению к вектору скорости кривой. Параллельный транспорт по геодезическим, «прямым линиям» поверхности, также легко описывается напрямую. Вектор в касательной плоскости транспортируется по геодезической как единственное векторное поле постоянной длины, составляющее постоянный угол с вектором скорости геодезической. Для общей кривой этот процесс необходимо изменить с помощью геодезической кривизны, которая измеряет, насколько кривая отклоняется от геодезической.

Векторное поле v ( t ) вдоль кривой единичной скорости c ( t ) с геодезической кривизной ( _kg t ) называется параллельным вдоль кривой, если

• он имеет постоянную длину
• угол θ ( t ) , который он образует с вектором скорости ċ ( t ), удовлетворяет

${\dot {\theta }}(t)=-k_{g}(t)$

Это восстанавливает правило параллельного транспорта вдоль геодезической или кусочной геодезической кривой, потому что в этом случае k _g = 0 , так что угол θ ( t ) должен оставаться постоянным на любом геодезическом сегменте. Существование параллельного переноса следует из того, что θ ( t ) можно вычислить как интеграл геодезической кривизны. Следовательно, поскольку оно непрерывно зависит от L ² нормы k _g , отсюда следует, что параллельный перенос для произвольной кривой может быть получен как предел параллельного переноса при аппроксимации кусочно-геодезических кривых.

Таким образом, связь можно описать в терминах подъема путей в многообразии к путям в касательном или ортонормированном расслоении реперов, тем самым формализуя классическую теорию « движущейся репера », которую предпочитают французские авторы. Подъемы петель вокруг точки приводят к образованию группы голономии в этой точке. Гауссова кривизна в точке может быть восстановлена ​​путем параллельного переноса по все более мелким петлям в этой точке. Эквивалентно кривизну можно вычислить непосредственно на бесконечно малом уровне в терминах скобок Ли поднятых векторных полей.

Эли Картан в 1904 году.

Соединение 1-форма

Подход Картана и Вейля, использующий 1-формы связности на расслоении реперов M , дает третий способ понять риманову связность. Они заметили, что параллельный транспорт требует, чтобы путь на поверхности был поднят до пути в пакете кадров так, чтобы его касательные векторы лежали в специальном подпространстве коразмерности один в трехмерном касательном пространстве пакета кадров. Проекция на это подпространство определяется дифференциальной 1-формой на расслоении ортонормированных реперов, формой связности . Это позволило закодировать свойства кривизны поверхности в дифференциальных формах на связке кадров и в формулах, включающих их внешние производные .

Этот подход особенно прост для встроенной поверхности. Благодаря результату Кобаяши (1956) связность 1-формы на поверхности, вложенной в евклидово пространство E ³ это просто возврат под отображением Гаусса 1-формы связности на S ² . Используя идентификацию S ² с однородным пространством SO(3)/SO(2) 1-форма связности является просто компонентом 1-формы Маурера – Картана на SO(3) .

Глобальная дифференциальная геометрия поверхностей

Хотя характеристика кривизны включает в себя только локальную геометрию поверхности, существуют важные глобальные аспекты, такие как теорема Гаусса-Бонне , теорема униформизации , теорема фон Мангольдта-Адамара и теорема вложимости. Есть и другие важные аспекты глобальной геометрии поверхностей. К ним относятся:

• Радиус инъективности , определяемый как наибольшее значение r , при котором две точки на расстоянии меньше r соединяются уникальной геодезической. Вильгельм Клингенберг доказал в 1959 году, что радиус инъективности замкнутой поверхности ограничен снизу минимумом δ = π / √sup . K и длину ее наименьшей замкнутой геодезической Это улучшило теорему Бонне, который показал в 1855 году, что диаметр замкнутой поверхности положительной гауссовой кривизны всегда ограничен сверху величиной δ ; другими словами, геодезическая, реализующая метрическое расстояние между двумя точками, не может иметь длину больше δ .
• Жесткость . В 1927 году Кон-Фоссен доказал, что два изометрических овалаоида — замкнутые поверхности с положительной гауссовой кривизной — обязательно конгруэнтны по изометрии E. ³ . Более того, замкнутая вложенная поверхность с положительной гауссовой кривизной и постоянной средней кривизной обязательно является сферой; аналогично замкнутая вложенная поверхность постоянной гауссовой кривизны должна быть сферой (Либманн, 1899). Хайнц Хопф показал в 1950 году, что замкнутая вложенная поверхность с постоянной средней кривизной и родом 0, т. е. гомеоморфная сфере, обязательно является сферой; пять лет спустя Александров снял топологическое предположение. В 1980-х годах Венте построил погруженные торы постоянной средней кривизны в евклидовом трехмерном пространстве.
• Гипотеза Каратеодори : Эта гипотеза утверждает, что замкнутая выпуклая трижды дифференцируемая поверхность допускает по крайней мере две омбилические точки . Первая работа по этой гипотезе была сделана в 1924 году Гансом Гамбургером , который отметил, что она следует из следующего более сильного утверждения: полуцелозначный индекс слоения главной кривизны изолированной пуповины не превосходит единицы.
• Нулевая гауссова кривизна : полная поверхность в E ³ с нулевой гауссовой кривизной должен быть цилиндром или плоскостью.
• Теорема Гильберта (1901 г.): никакая полная поверхность постоянной отрицательной кривизны не может быть изометрически погружена в E. ³ .

Кратчайшая петля на торе

• Уиллмора Гипотеза . Эта гипотеза утверждает, что интеграл от квадрата средней кривизны тора, погруженного в E ³ должно быть ограничено снизу 2π ² . Известно, что интеграл инвариант Мебиуса. Ее решили в 2012 году Фернандо Кода Маркес и Андре Невес .
• Изопериметрические неравенства . В 1939 году Шмидт доказал, что классическое изопериметрическое неравенство для кривых в евклидовой плоскости также справедливо на сфере или в гиперболической плоскости: а именно, он показал, что среди всех замкнутых кривых, ограничивающих область фиксированной площади, периметр минимизируется, когда кривая представляет собой круг для метрики. В одном измерении выше известно, что среди всех замкнутых поверхностей в E ³ возникая как граница ограниченной области единичного объема, площадь поверхности евклидова шара минимизируется.
• Систолические неравенства для кривых на поверхностях . Для замкнутой поверхности ее систола определяется как наименьшая длина любой несжимаемой замкнутой кривой на поверхности. В 1949 году Лёвнер доказал неравенство тора для метрик на торе, а именно, что площадь тора над квадратом его систолы ограничена снизу √ 3/2 ) . с равенством в плоском случае (постоянной кривизны Аналогичный результат дает неравенство Пу для вещественной проективной плоскости 1952 года с нижней границей 2 / π достигается и в случае постоянной кривизны. Для бутылки Клейна Блаттер и Бавард позже получили нижнюю границу √ 8 / π . Для замкнутой поверхности рода g Хебда и Бураго показали, что отношение ограничено снизу соотношением 1/2 ​ ​ . Три года спустя Михаил Громов нашел нижнюю оценку, заданную постоянным временем g ^{1 ⁄ 2} , хотя это не оптимально. Асимптотически точные верхние и нижние оценки, заданные постоянными временами г / (логг г ) ² принадлежат Громову и Бузеру-Сарнаку, их можно найти у Каца (2007) . Существует также версия для метрики на сфере, принимая за систолу длину наименьшей замкнутой геодезической . Громов предположил нижнюю границу 1/2 году: лучший результат на в 1980 √ 3 данный момент — это нижняя граница 1/8 году . получена Региной Ротман в 2006

Руководство по чтению

Один из наиболее полных вводных обзоров предмета, описывающий историческое развитие от до Гаусса до наших дней, принадлежит Бергеру (2004) . Изложения классической теории даны в работах Эйзенхарта (2004) , Крейцига (1991) и Струика (1988) ; более современные, обильно иллюстрированные учебники для студентов Грея, Аббены и Саламона (2006) , Прессли (2001) и Уилсона (2008) могут оказаться более доступными. Доступное изложение классической теории можно найти у Гильберта и Кон-Фоссена (1952) . Более сложные методы лечения на уровне выпускников с использованием римановой связи на поверхности можно найти в работах Singer & Thorpe (1967) , do Carmo (2016) и O'Neill (2006) .

См. также

• Касательный вектор
• дюймовая поверхность

Ссылки

• Эндрюс, Бен; Брайан, Пол (2010), «Границы кривизны путем изопериметрического сравнения для нормализованного потока Риччи на двух сферах», Calc. Вар. Уравнения в частных производных , 39 (3–4): 419–428, arXiv : 0908.3606 , doi : 10.1007/s00526-010-0315-5 , S2CID   1095459
• Арнольд, В.И. (1989), Математические методы классической механики , Тексты для аспирантов по математике, том. 60 (2-е изд.), Нью-Йорк: Springer-Verlag, ISBN.  978-0-387-90314-9 ; перевод с русского К. Фогтмана и А. Вайнштейна.
• Бергер, Марсель (2004), Панорамный вид римановой геометрии , Springer-Verlag, ISBN  978-3-540-65317-2
• Бергер, Мелвин С. (1977), Нелинейность и функциональный анализ , Academic Press, ISBN  978-0-12-090350-4
• Бонола, Роберто; Карслоу, HS; Энрикес, Ф. (1955), Неевклидова геометрия: критическое и историческое исследование ее развития , Дувр, ISBN  978-0-486-60027-7
• Бутби, Уильям М. (1986), Введение в дифференцируемые многообразия и риманову геометрию , Чистая и прикладная математика, том. 120 (2-е изд.), Academic Press, ISBN  0121160521
• Картан, Эли (1983), Геометрия римановых пространств , Math Sci Press, ISBN  978-0-915692-34-7 ; перевод из 2-го издания «Уроков геометрии римановых пространств» (1951) Джеймса Глейзбрука.
• Картан, Эли (2001), Риманова геометрия в ортогональной системе координат (из лекций, прочитанных Э. Картаном в Сорбонне в 1926–27 гг.) (PDF) , World Scientific, ISBN  978-981-02-4746-1 ; перевод с русского В. В. Гольдберга с предисловием С. С. Черна .
• Картан, Анри (1971), Calcul Differentiel (на французском языке), Герман , ISBN  9780395120330
• Чен, Сюсюн; Лу, Пэн; Тиан, Ганг (2006), «Заметки об униформизации римановых поверхностей потоком Риччи», Proc. AMS , 134 (11): 3391–3393, номер документа : 10.1090/S0002-9939-06-08360-2.
• Черн, С.С. (1967), Кривые и поверхности в евклидовых пространствах , Исследования MAA по математике, Математическая ассоциация Америки
• Чоу, Б. (1991), «Поток Риччи на двумерной сфере», J. Diff. Геом. , 33 (2): 325–334, doi : 10.4310/jdg/1214446319
• Курант, Ричард (1950), Принцип Дирихле, конформное отображение и минимальные поверхности , John Wiley & Sons, ISBN  978-0-486-44552-6
• Дарбу, Гастон , Уроки общей теории поверхностей , Готье-Виллар Том I (1887 г.) , Том II (1915 г.) [1889 г.] , Том III (1894 г.) , Том IV (1896 г.) .
• Динг, В. (2001), "Доказательство теоремы униформизации S ² ", Дж. Уравнения в частных производных , 14 : 247–250.
• ду Кармо, Манфредо П. (2016), Дифференциальная геометрия кривых и поверхностей (переработанное и обновленное 2-е изд.), Минеола, Нью-Йорк: Dover Publications, Inc., ISBN  978-0-486-80699-0
• ду Карму, Манфредо (1992), Риманова геометрия , Математика: теория и приложения, Биркхойзер, ISBN  0-8176-3490-8
• Эйзенхарт, Лютер Пфалер (2004), Трактат о дифференциальной геометрии кривых и поверхностей (перепечатка издания 1909 года), Dover Publications, Inc., ISBN  0-486-43820-1
• Эйлер, Леонхард (1760), «Исследование кривизны поверхностей» , Мемуары Берлинской академии наук , 16 (опубликовано в 1767 году): 119–143 .
• Эйлер, Леонхард (1771), «О твердых телах, поверхность которых можно объяснить на плоскости» , Новые комментарии Петрополитанской академии наук , 16 (опубликовано в 1772 году): 3–34 .
• Гаусс, Карл Фридрих (1902), Общие исследования искривленных поверхностей 1825 и 1827 годов , Библиотека Принстонского университета , перевод А. М. Хилтебейтеля и Дж. К. Морхеда; «Общие дискуссии относительно криволинейных поверхностей» , Труды Королевского общества наук Геттингена, Vol. 6 (1827), с. 99–146.
  • Гаусс, Карл Фридрих (1965), Общие исследования искривленных поверхностей , перевод А. М. Хилтебайтеля; Джей Си Морхед, Хьюлетт, Нью-Йорк: Raven Press, OCLC   228665499 .
  • Гаусс, Карл Фридрих (2005), Общие исследования изогнутых поверхностей , отредактированный с новым введением и примечаниями Питера Песича, Минеола, Нью-Йорк: Dover Publications, ISBN  978-0-486-44645-5 .
• Грей, Альфред; Аббена, Эльза; Саламон, Саймон (2006), Современная дифференциальная геометрия кривых и поверхностей с помощью Mathematica® , Исследования по высшей математике (3-е изд.), Бока-Ратон, Флорида: Chapman & Hall/CRC, ISBN  978-1-58488-448-4
• Хан, Цин; Хун, Цзя-Син (2006), Изометрическое вложение римановых многообразий в евклидовы пространства , Американское математическое общество, ISBN  978-0-8218-4071-9
• Хельгасон, Сигурдур (1978), Дифференциальная геометрия, группы Ли и симметричные пространства , Academic Press, Нью-Йорк, ISBN  978-0-12-338460-7
• Гильберт, Дэвид ; Кон-Воссен, Стефан (1952), Геометрия и воображение (2-е изд.), Нью-Йорк: Челси, ISBN  978-0-8284-1087-8
• Хитчин, Найджел (2013), Геометрия поверхностей (PDF)
• Хопф, Хайнц (1989), Лекции по дифференциальной геометрии в целом , Конспекты лекций по математике, том. 1000, Шпрингер-Верлаг, ISBN  978-3-540-51497-8
• Имаёси, Ю.; Танигучи, М. (1992), Введение в пространства Техмюллера , Springer-Verlag, ISBN  978-0-387-70088-5
• Айви, Томас А.; Ландсберг, Дж. М. (2003), Картан для начинающих: дифференциальная геометрия с помощью движущихся систем отсчета и внешних систем , Аспирантура по математике, том. 61, Американское математическое общество, ISBN.  978-0-8218-3375-9
• Кац, Михаил Г. (2007), Систолическая геометрия и топология , Математические обзоры и монографии, том. 137, Американское математическое общество, ISBN.  978-0-8218-4177-8
• Милнор, Дж. (1963). Теория Морса . Анналы математических исследований. Том. 51. Принстон, Нью-Джерси: Издательство Принстонского университета. МР   0163331 . Збл   0108.10401 .
• Кобаяши, Шошичи (1956), «Индуцированные связи и вложенное риманово пространство», Nagoya Math. Дж. , 10 : 15–25, doi : 10.1017/S0027763000000052
• Кобаяши, Шошичи (1957), «Теория связей», Анналы чистой и прикладной математики , серия 4, 43 : 119–194, doi : 10.1007/BF02411907 , S2CID   120972987 ,
• Кобаяши, Сошичи, Номидзу, Кацуми (1963), Основы дифференциальной геометрии, Том I , Wiley Interscience, ISBN.  978-0-470-49648-0
• Кобаяши, Шошичи; Номидзу, Кацуми (1969), Основы дифференциальной геометрии, Том. II , Wiley Interscience, ISBN  978-0-470-49648-0
• Крейциг, Эрвин (1991), Дифференциальная геометрия , Дувр, ISBN  978-0-486-66721-8
• Кюнель, Вольфганг (2006), Дифференциальная геометрия: кривые – поверхности – многообразия , Американское математическое общество, ISBN  978-0-8218-3988-1
• Леви-Чивита, Туллио (1917), «Понятие параллелизма в любом многообразии» , Ренд. Цирк. Мэтт. Палермо , 42 : 173–205, номер документа : 10.1007/BF03014898 , S2CID   122088291.
• О'Нил, Барретт (2006), Элементарная дифференциальная геометрия (пересмотренное 2-е изд.), Амстердам: Elsevier/Academic Press, ISBN  0-12-088735-5
• Осгуд, Б.; Филлипс, Р.; Сарнак, П. (1988), "Экстремали определителей лапласианов", J. Funct. Анальный. , 80 : 148–211, doi : 10.1016/0022-1236(88)90070-5
• Оссерман, Роберт (2002), Обзор минимальных поверхностей , Дувр, ISBN  978-0-486-49514-9
• Ян Р. Портеус (2001) Геометрическая дифференциация: для интеллекта кривых и поверхностей , Cambridge University Press ISBN   0-521-00264-8 .
• Прессли, Эндрю (2001), Элементарная дифференциальная геометрия , серия Springer по математике для студентов, Springer-Verlag, ISBN  978-1-85233-152-8
• Сакс, Дж.; Уленбек, Карен (1981), «Существование минимальных погружений двухсфер», Ann. математики. , 112 (1): 1–24, номер документа : 10.2307/1971131 , JSTOR   1971131.
• Певец, Исадор М .; Торп, Джон А. (1967), Конспекты лекций по элементарной топологии и геометрии , Springer-Verlag, ISBN  978-0-387-90202-9
• Спивак, Майкл (1965), Исчисление на многообразиях. Современный подход к классическим теоремам продвинутого исчисления , В.А. Бенджамин.
• Стиллвелл, Джон (1996), Источники гиперболической геометрии , Американское математическое общество, ISBN  978-0-8218-0558-9
• Струик, Дирк (1987), Краткая история математики (4-е изд.), Dover Publications, ISBN  0486602559
• Струик, Дирк Дж. (1988) [1961], Лекции по классической дифференциальной геометрии (переиздание 2-го изд.), Нью-Йорк: Dover Publications, Inc., ISBN  0-486-65609-8
• Тейлор, Майкл Э. (1996a), Уравнения в частных производных II: Качественные исследования линейных уравнений , Springer-Verlag, ISBN  978-1-4419-7051-0
• Тейлор, Майкл Э. (1996b), Уравнения в частных производных III: Нелинейные уравнения , Springer-Verlag, ISBN  978-1-4419-7048-0
• Thorpe, John A. (1994), Elementary topics in differential geometry, Undergraduate Texts in Mathematics, Springer-Verlag, ISBN 0387903577
• Toponogov, Victor A. (2005), Differential Geometry of Curves and Surfaces: A Concise Guide, Springer-Verlag, ISBN 978-0-8176-4384-3
• Valiron, Georges (1986), The Classical Differential Geometry of Curves and Surfaces, Math Sci Press, ISBN 978-0-915692-39-2 Full text of book
• Warner, Frank W. (1983), Foundations of differentiable manifolds and Lie groups, Graduate Texts in Mathematics, vol. 94, Springer, ISBN 0-387-90894-3
• Wells, R. O. (2017), Differential and complex geometry: origins, abstractions and embeddings, Springer, ISBN 9783319581842
• Wilson, Pelham (2008), Curved Space: From Classical Geometries to Elementary Differential Geometry, Cambridge University Press, ISBN 978-0-521-71390-0

External links

• Media related to Differential geometry of surfaces at Wikimedia Commons