Трактрикс

Tractrix создается с помощью конца шеста (лежащего на земле). Другой его конец сначала толкают, а затем тянут пальцем, пока он вращается в одну сторону.

В геометрии трактриса , прикрепленным к (от латинского trahere «тянуть, тащить»; множественное число: tractrices ) — это кривая , по которой движется объект под действием трения , когда его тянут в горизонтальной плоскости отрезком линии точке тяги. ( трактор ), который движется под прямым углом к начальной линии между объектом и съемником с бесконечно малой скоростью. Следовательно, это кривая преследования . Впервые он был введен Клодом Перро в 1670 году, а позже изучен Исааком Ньютоном (1676 год) и Христианом Гюйгенсом (1693 год). ^[1]

Математический вывод

Трактрикс с объектом изначально в $(4, 0)$

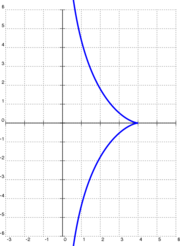
Предположим, что объект помещен в точку $(a, 0)$ (или $(4, 0)$ в примере, показанном справа), а съемник - в начале координат , поэтому $a$ - длина тянущей нити (4 в примере справа). . Затем съемник начинает двигаться вдоль $оси y$ в положительном направлении. В каждый момент нить будет касаться кривой $y = y (x),$ описываемой объектом, так что она станет полностью определяться движением съемника. Математически, если координаты объекта $(x, y)$ , $y$ координата съемника равна $y+\operatorname {sign} (y){\sqrt {a^{2}-x^{2}}},$ по теореме Пифагора . Запись о том, что наклон резьбы равен наклону касательной к кривой, приводит к дифференциальному уравнению

{\frac {dy}{dx}}=\pm {\frac {\sqrt {a^{2}-x^{2}}}{x}}

с начальным условием $y (a) = 0$ . Его решение

y=\int _{x}^{a}{\frac {\sqrt {a^{2}-t^{2}}}{t}}\,dt=\pm \!\left(a\ln {\frac {a+{\sqrt {a^{2}-x^{2}}}}{x}}-{\sqrt {a^{2}-x^{2}}}\right),

где знак $\pm$ зависит от направления (положительного или отрицательного) движения съемника.

Первый член этого решения также можно записать

a\operatorname {arsech} {\frac {x}{a}},

где $arsech$ — обратная гиперболическая секансная функция.

Знак перед решением зависит от того, движется ли съемник вверх или вниз. Обе ветви принадлежат трактрисе и встречаются в возврата точке $(a, 0)$ .

Основа трактрикса

Существенным свойством трактрисы является постоянство расстояния между точкой $P$ на кривой и пересечением касательной в точке P $с$ асимптотой кривой .

Трактрикс можно рассматривать по-разному:

Это геометрическое место центра гиперболической спирали , катящейся (без заноса) по прямой.
Это эвольвента цепной , однородную струну , функции, которая описывает полностью гибкую, неупругую прикрепленную к двум точкам и находящуюся под действием гравитационного поля. Цепная сеть имеет уравнение $y ( x ) = a ch .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ x / a ⁠$ .
Траектория, определяемая серединой задней оси автомобиля, тянутого тросом с постоянной скоростью и с постоянным направлением (первоначально перпендикулярно автомобилю).
Это (нелинейная) кривая, которую круг радиуса $a,$ катящийся по прямой, с центром на $оси x$ , всегда перпендикулярно пересекает.

Функция допускает горизонтальную асимптоту. Кривая симметрична относительно $оси y$ . Радиус $r = кроватка кривизны ⁠ x / y ⁠$ .

Важным значением, которое имело трактриса, было изучение ее поверхности вращения вокруг ее асимптоты: псевдосферы . Изучен Эухенио Бельтрами в 1868 году. ^[2] Как поверхность постоянной отрицательной гауссовой кривизны , псевдосфера является локальной моделью гиперболической геометрии . Идея была развита Каснером и Ньюманом в их книге «Математика и воображение» , где они показывают игрушечный поезд, тянущий карманные часы для создания трактрисы. ^[3]

Характеристики

Кривую можно параметризовать уравнением $x=t-\tanh(t),y=1/{\cosh(t)}$ . ^[4]
Благодаря геометрическому способу определения трактриса обладает тем свойством, что отрезок ее касательной между асимптотой и точкой касания имеет постоянную длину $a$ .
Длина дуги одной ветви $x = x 1$ и $x = x 2$ равна $ln между ⁠ x 1 / x 2 ⁠$ .
Площадь между трактрисой и ее асимптотой равна $⁠ π а 2 / 2 ⁠$ , который можно найти с помощью интегрирования или теоремы Мамикона .
Огибающая трактрисы ( нормалей ) , то есть эволюта трактрисы) представляет собой цепную линию (или цепную кривую заданную формулой $y = a ch ⁠ x / a ⁠$ .
Поверхность вращения, создаваемая вращением трактрисы вокруг своей асимптоты, представляет собой псевдосферу .
Трактриса — трансцендентная кривая ; его нельзя определить полиномиальным уравнением.

Практическое применение

В 1927 году П.Г.А.Х. Фойгт запатентовал конструкцию рупорного громкоговорителя , основанную на предположении, что волновой фронт, проходящий через рупор, имеет сферическую форму постоянного радиуса. Идея состоит в том, чтобы минимизировать искажения, вызванные внутренним отражением звука внутри рупора. Полученная форма является поверхностью вращения трактрисы. ^[5]
Важным применением является технология формовки листового металла. В частности, профиль tractrix используется для угла штампа, на котором листовой металл сгибается во время глубокой вытяжки. ^[6]

Конструкция шкива с зубчатым ремнем обеспечивает повышенную эффективность передачи механической мощности за счет использования цепной формы зубьев трактриса. ^[7] Такая форма сводит к минимуму трение зубьев ремня, входящих в контакт со шкивом, поскольку движущиеся зубья входят в зацепление и выключаются с минимальным скользящим контактом. В оригинальной конструкции ремня ГРМ использовались более простой трапециевидной зубья или круглой формы, которые вызывают значительное скольжение и трение.

Чертежные машины

В октябре – ноябре 1692 года Христиан Гюйгенс описал три машины для рисования трактрисов. ^[8]
В 1693 году Готфрид Вильгельм Лейбниц изобрел «универсальную тяговую машину», которая теоретически могла интегрировать любое дифференциальное уравнение первого порядка . ^[9] Идея представляла собой аналоговый вычислительный механизм, реализующий тяговый принцип. Устройство было непрактично создавать с использованием технологий времен Лейбница, и оно так и не было реализовано.
В 1706 году Джон Перкс построил тяговую машину для реализации гиперболической квадратуры. ^[10]
В 1729 году Джованни Полени построил тяговое устройство, позволяющее логарифмические функции . чертить ^[11]

Историю всех этих машин можно посмотреть в статье HJM Bos . ^[8]

См. также

поверхность Дини
Гиперболические функции для $tanh$ , $sech$ , $csch$ , $arcosh$
Натуральный логарифм для $ln$
Функция знака для $знака$
Тригонометрические функции для $sin$ , $cos$ , $tan$ , $arccot$ , $csc$

Примечания

^ Стиллвелл, Джон (2010). Математика и ее история (переработанное, 3-е изд.). Springer Science & Business Media. п. 345. ИСБН 978-1-4419-6052-8 . , выдержка со стр. 345
^ Бельтрами, Э. (1868). «Очерк интерпретации неевклидовой геометрии». Журнал математики . 6 : 284. Цит. Бертотти, Бруно; Катеначчи, Роберто; Дапьяджи, Клаудио (2007). «Псевдосферы в геометрии и физике: от Бельтрами до де Ситтера и далее». Великий математик XIX века. Документы в честь Эудженио Бельтрами (1835–1900) (итальянский) . Ист. Ломбардо Аккад. наук. Летт. Неконтр. Студия. Том. 39. ЛЭД – Ред. унив. Летт. Экон. Диритто, Милан. стр. 165–194. arXiv : math/0506395 . ISBN 978-88-7916-359-0 . МР 2374676 .
^ Каснер, Эдвард; Ньюман, Джеймс (2013). «Рисунок 45(а)» . Математика и воображение . Дуврские книги по математике. Курьерская корпорация. п. 141. ИСБН 9780486320274 .
^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Tractrix» , Архив истории математики MacTutor , Университет Сент-Эндрюс
^ Конструкция рупорного громкоговорителя, стр. 4–5. (Перепечатано из журнала Wireless World, март 1974 г.)
^ Ланге, Курт (1985). Справочник по обработке металлов давлением . Книжная компания Макгроу Хилл. п. 20.43.
^ «Руководство по проектированию привода Gates Powergrip GT3» (PDF) . Корпорация Гейтс . 2014. с. 177 . Проверено 17 ноября 2017 г. Профиль зубьев GT основан на математической функции трактикс. В инженерных справочниках эта функция описывается как система «без трения». Это раннее развитие Шиле описывается как эвольвентная форма цепной линии.
^ Jump up to: Перейти обратно: ^а ^б Бос, HJM (1989). «Признание и чудо - Гюйгенс, тяговое движение и некоторые мысли об истории математики» (PDF) . Евклид . 63 : 65–76.
^ Миличи, Пьетро (2014). Лолли, Габриэле (ред.). От логики к практике: итальянские исследования в области философии математики . Спрингер. ...механические устройства, изучаемые... для решения частных дифференциальных уравнений... Надо вспомнить «универсальную тяговую машину» Лейбница.
^ Перкс, Джон (1706). «Построение и свойства новой квадратрисы гиперболы». Философские труды . 25 : 2253–2262. дои : 10.1098/rstl.1706.0017 . JSTOR 102681 . S2CID 186211499 .
^ Полени, Джон (1729). Сборник математических букв . п. письмо № 7.

Ссылки

Каснер, Эдвард; Ньюман, Джеймс (1940). Математика и воображение . Саймон и Шустер . п. 141–143 .
Лоуренс, Дж. Деннис (1972). Каталог специальных плоских кривых . Дуврские публикации. стр. 5, 199 . ISBN 0-486-60288-5 .

Внешние ссылки

О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Tractrix» , Архив истории математики MacTutor , Университет Сент-Эндрюс
«Трактрикс» . ПланетаМатематика .
«Знаменитые кривые» . ПланетаМатематика .
Трактрикс на MathWorld
Модуль: Карманные часы Лейбница «ОДА» в PHASER

[1] Стиллвелл, Джон (2010). Математика и ее история (переработанное, 3-е изд.). Springer Science & Business Media. п. 345. ИСБН 978-1-4419-6052-8 . , выдержка со стр. 345

[2] Бельтрами, Э. (1868). «Очерк интерпретации неевклидовой геометрии». Журнал математики . 6 : 284. Цит. Бертотти, Бруно; Катеначчи, Роберто; Дапьяджи, Клаудио (2007). «Псевдосферы в геометрии и физике: от Бельтрами до де Ситтера и далее». Великий математик XIX века. Документы в честь Эудженио Бельтрами (1835–1900) (итальянский) . Ист. Ломбардо Аккад. наук. Летт. Неконтр. Студия. Том. 39. ЛЭД – Ред. унив. Летт. Экон. Диритто, Милан. стр. 165–194. arXiv : math/0506395 . ISBN 978-88-7916-359-0 . МР 2374676 .

[3] Каснер, Эдвард; Ньюман, Джеймс (2013). «Рисунок 45(а)» . Математика и воображение . Дуврские книги по математике. Курьерская корпорация. п. 141. ИСБН 9780486320274 .

[4] О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Tractrix» , Архив истории математики MacTutor , Университет Сент-Эндрюс

[5] Конструкция рупорного громкоговорителя, стр. 4–5. (Перепечатано из журнала Wireless World, март 1974 г.)

[6] Ланге, Курт (1985). Справочник по обработке металлов давлением . Книжная компания Макгроу Хилл. п. 20.43.

[7] «Руководство по проектированию привода Gates Powergrip GT3» (PDF) . Корпорация Гейтс . 2014. с. 177 . Проверено 17 ноября 2017 г. Профиль зубьев GT основан на математической функции трактикс. В инженерных справочниках эта функция описывается как система «без трения». Это раннее развитие Шиле описывается как эвольвентная форма цепной линии.

[bos-8] Jump up to: Перейти обратно: ^а ^б Бос, HJM (1989). «Признание и чудо - Гюйгенс, тяговое движение и некоторые мысли об истории математики» (PDF) . Евклид . 63 : 65–76.

[9] Миличи, Пьетро (2014). Лолли, Габриэле (ред.). От логики к практике: итальянские исследования в области философии математики . Спрингер. ...механические устройства, изучаемые... для решения частных дифференциальных уравнений... Надо вспомнить «универсальную тяговую машину» Лейбница.

[10] Перкс, Джон (1706). «Построение и свойства новой квадратрисы гиперболы». Философские труды . 25 : 2253–2262. дои : 10.1098/rstl.1706.0017 . JSTOR 102681 . S2CID 186211499 .

[11] Полени, Джон (1729). Сборник математических букв . п. письмо № 7.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]