Монодромия

В математике , монодромия — это изучение того, как ведут себя объекты математического анализа , алгебраической топологии , алгебраической геометрии и дифференциальной геометрии когда они «оббегают» особенность . Как следует из названия, основной смысл монодромии заключается в «беге в одиночку». Оно тесно связано с покрытием карт и их вырождением в разветвление ; Аспект, вызывающий явления монодромии, заключается в том, что некоторые функции, которые мы, возможно, пожелаем определить, не могут быть однозначными , когда мы «оббегаем» путь, охватывающий сингулярность. Несостоятельность монодромии можно измерить, определив группу монодромии : группу преобразований, действующих на данные, которые кодируют то, что происходит, когда мы «бегаем» в одном измерении. Отсутствие монодромии иногда называют полидромией . ^[1]

Определение [ править ]

Пусть $X$ — связное и локально связное основанное топологическое пространство с базовой точкой $x$ , и пусть $p:{\tilde {X}}\to X$ быть покрытием из волокна $F=p^{-1}(x)$ . Для петли $γ: [0, 1] \to X$ , базирующейся в точке $x$ , обозначим подъем под картой покрытия, начинающийся в точке ${\tilde {x}}\in F$ , к ${\tilde {\gamma }}$ . Наконец, обозначим через ${\tilde {x}}\cdot {\tilde {\gamma }}$ конечная точка ${\tilde {\gamma }}(1)$ , что в целом отличается от ${\tilde {x}}$ . Существуют теоремы, которые утверждают, что эта конструкция дает четко определенное групповое действие фундаментальной группы $π 1 (X, x)$ на $F$ и стабилизатор что ${\tilde {x}}$ это точно $p_{*}\left(\pi _{1}\left({\tilde {X}},{\tilde {x}}\right)\right)$ , то есть элемент $[γ]$ фиксирует точку в $F$ тогда и только тогда, когда он представлен образом петли в ${\tilde {X}}$ на базе ${\tilde {x}}$ . Это действие называется действием монодромии , а соответствующий гомоморфизм $π 1 (X, x) \to Aut(H * (F x))$ в группу автоморфизмов на $F$ является алгебраической монодромией . Образом этого гомоморфизма является группа монодромии . Существует другое отображение $π 1 (X, x) \to Diff(F x)/Is(F x),$ образ которого называется топологической группой монодромии .

Пример [ править ]

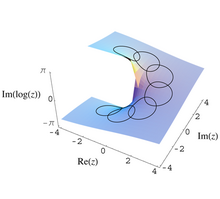
Эти идеи были впервые сформулированы в комплексном анализе . В процессе аналитического продолжения функция, являющаяся аналитической функцией $F (z)$ в некотором открытом подмножестве $E$ проколотой комплексной плоскости $\mathbb {C} \backslash \{0\}$ может быть продолжено обратно в $E$ , но с другими значениями. Например, возьмите

{\begin{aligned}F(z)&=\log(z)\\E&=\{z\in \mathbb {C} \mid \operatorname {Re} (z)>0\}\end{aligned}}

затем аналитическое продолжение против часовой стрелки по кругу

|z|=1

приведет к возврату не к $F (z),$ а

F(z)+2\pi i

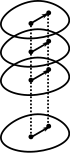
В этом случае группа монодромии является бесконечной циклической , а накрытием является универсальное накрытие проколотой комплексной плоскости. Это покрытие можно представить как геликоид (как определено в статье о геликоиде), ограниченный до $ρ > 0$ . Покрывающая карта представляет собой вертикальную проекцию, в каком-то смысле очевидным образом сжимающую спираль, чтобы получить проколотую плоскость.

Дифференциальные уравнения в комплексной области [ править ]

Одним из важных приложений являются дифференциальные уравнения , где одно решение может дать дальнейшие линейно независимые решения путем аналитического продолжения . определенные в открытом связном множестве S которая (точнее) является линейным представлением фундаментальной группы S Линейные дифференциальные уравнения , , суммирующей все аналитические продолжения вокруг петель внутри S. на комплексной плоскости, имеют группу монодромии , Обратная задача построения уравнения (с регулярными особенностями ) по заданному представлению называется проблемой Римана–Гильберта .

Для регулярной (и, в частности, фуксовой) линейной системы в качестве образующих группы монодромии обычно выбирают операторы Mj _, соответствующие петлям, каждая из которых обходит только один из полюсов системы против часовой стрелки. Если индексы j выбраны таким образом, что они увеличиваются от 1 до p + 1 при обходе базовой точки по часовой стрелке, то единственным соотношением между образующими является равенство $M_{1}\cdots M_{p+1}=\operatorname {id}$ . Проблема Делиня–Симпсона представляет собой следующую проблему реализации: для каких наборов классов сопряженности в GL( n , C ) существуют неприводимые наборы матриц M _j из этих классов, удовлетворяющие указанному выше соотношению? Проблема была сформулирована Пьером Делинем , а Карлос Симпсон первым получил результаты в направлении ее решения. Аддитивная версия проблемы о невязках фуксовых систем была сформулирована и исследована Владимиром Костовым . Проблема рассматривалась другими авторами для матричных групп, отличных от GL( n , C ). и ^[2]

и Топологические аспекты геометрические

В случае покрывающего отображения мы рассматриваем его как частный случай расслоения и используем свойство гомотопического подъема , чтобы «следовать» по путям в базовом пространстве X (для простоты мы предполагаем, что оно линейно связно ), когда они поднимаются. в крышку C . Если мы пройдем по циклу, основанному на x в X , который мы поднимем, чтобы начать с c выше x , мы закончим в некотором c* снова выше x ; вполне возможно, что c ≠ c* , и для кодирования этого рассматривается действие фундаментальной группы $π$ ₁ ( X , x ) как группы перестановок на множестве всех c , как группы монодромии в этом контексте.

В дифференциальной геометрии аналогичную роль играет параллельный перенос . В главном расслоении B над гладким многообразием M связность m допускает «горизонтальное» перемещение от слоев выше в M к соседним. Эффект при применении к циклам, основанным на m, заключается в определении группы голономии переводов волокна в m ; если структурная группа B равна G , это подгруппа G которая измеряет отклонение B от пучка продуктов M × G. ,

Группоид монодромии слоения и

По аналогии с фундаментальным группоидом можно избавиться от выбора базовой точки и определить монодромный группоид. Здесь мы рассматриваем (гомотопические классы) лифты путей в базовом пространстве X расслоения $p:{\tilde {X}}\to X$ . Результат имеет структуру группоида над базовым X. пространством что мы можем отказаться от условия связности X. Преимущество в том ,

Более того, конструкцию можно обобщить и на слоения : рассмотрим $(M,{\mathcal {F}})$ (возможно, сингулярное) слоение M . Тогда для каждого пути в листе ${\mathcal {F}}$ мы можем рассмотреть его индуцированный диффеоморфизм на локальных трансверсальных сечениях, проходящих через концы. В пределах односвязной карты этот диффеоморфизм становится единственным и особенно каноническим между различными трансверсальными сечениями, если мы перейдем к зародышу диффеоморфизма вокруг концов. Таким образом, он также становится независимым от пути (между фиксированными конечными точками) внутри односвязной карты и, следовательно, инвариантен относительно гомотопии.

через Галуа Определение теорию

Обозначим через F ( x ) поле рациональных функций по переменной x над полем F , которое является полем частных F кольца многочленов [ x ] . Элемент y = f ( x ) из F ( x ) определяет конечное расширение поля [ F ( x ): F ( y )].

Это расширение обычно не является расширением Галуа, но имеет замыкание Галуа L ( f ). Соответствующая группа Галуа расширения [ L ( f ) : F ( y )] называется группой монодромии f .

В случае F = C вступает в силу теория римановой поверхности , допускающая приведенную выше геометрическую интерпретацию. В случае, если расширение [ C ( x ): C ( y )] уже является Галуа, ассоциированную группу монодромии иногда называют группой преобразований колоды .

Это связано с теорией Галуа накрытия пространств, приводящей к теореме существования Римана .

См. также [ править ]

Группа кос
Теорема о монодромии
Группа классов сопоставления (проколотого диска)

Примечания [ править ]

^ Король, Вольфганг; Шпрекельс, Юрген (2015). Карл Вейерштрасс (1815–1897): аспекты его жизни и творчества (на немецком языке). Издательство Спрингер. стр. 200–201. ISBN 9783658106195 . Проверено 5 октября 2017 г.
^ В. П. Костов (2004), «Проблема Делиня–Симпсона — обзор», J. Algebra , 281 (1): 83–108, arXiv : math/0206298 , doi : 10.1016/j.jalgebra.2004.07.013 , MR 2091962 , S2CID 119634752 и ссылки в нем.

Ссылки [ править ]

В.И. Данилов (2001) [1994], «Монодромия» , Энциклопедия Математики , EMS Press
«Группоиды и группоиды монодромии», О. Мучук, Б. Кылычарслан, Т. Сахан, Н. Алемдар, Топология и ее приложения 158 (2011) 2034–2042 doi: 10.1016/j.topol.2011.06.048
Р. Браун Топология и группоиды (2006).
П. Дж. Хиггинс, «Категории и группоиды», ван Ностранд (1971) TAC Reprint
Х. Жолондек, «Группа монодромии», Birkhäuser Basel, 2006; дои: 10.1007/3-7643-7536-1

[König2015-1] Король, Вольфганг; Шпрекельс, Юрген (2015). Карл Вейерштрасс (1815–1897): аспекты его жизни и творчества (на немецком языке). Издательство Спрингер. стр. 200–201. ISBN 9783658106195 . Проверено 5 октября 2017 г.

[2] В. П. Костов (2004), «Проблема Делиня–Симпсона — обзор», J. Algebra , 281 (1): 83–108, arXiv : math/0206298 , doi : 10.1016/j.jalgebra.2004.07.013 , MR 2091962 , S2CID 119634752 и ссылки в нем.

[1]

[2]