Поле (математика)

Эта статья об алгебраической структуре. Для векторных функций см. векторное поле . Чтобы узнать о других значениях, см. Поле (значения) § Математика .

Правильный линейку семиугольник невозможно построить, используя только и циркуль ; это можно доказать, используя поле конструктивных чисел .

В математике поле набор — это , на котором сложение , вычитание , умножение и деление определены , которые ведут себя как соответствующие операции над рациональными и действительными числами . Таким образом, поле представляет собой фундаментальную алгебраическую структуру , которая широко используется в алгебре , теории чисел и многих других областях математики.

Наиболее известными полями являются поле рациональных чисел , поле действительных чисел и поле комплексных чисел . Многие другие поля, такие как поля рациональных функций , поля алгебраических функций , поля алгебраических чисел и p -адические поля , обычно используются и изучаются в математике, особенно в теории чисел и алгебраической геометрии . Большинство криптографических протоколов полагаются на конечные поля , т. е. поля с конечным числом элементов .

Теория полей доказывает, что трисекцию угла и квадратуру круга невозможно выполнить с помощью циркуля и линейки . Теория Галуа , посвященная пониманию симметрий расширений полей , дает изящное доказательство теоремы Абеля-Руффини о том, что общие уравнения пятой степени не могут быть решены в радикалах .

Поля служат основополагающими понятиями в нескольких математических областях. Сюда входят различные разделы математического анализа , в основе которых лежат поля с дополнительной структурой. Основные теоремы анализа зависят от структурных свойств поля действительных чисел. Что наиболее важно для алгебраических целей, любое поле может использоваться в качестве скаляров для векторного пространства , которое является стандартным общим контекстом для линейной алгебры . Числовые поля , братья и сестры поля рациональных чисел, глубоко изучаются в теории чисел . Поля функций могут помочь описать свойства геометрических объектов.

Определение

Неформально, поле представляет собой набор вместе с двумя операциями , определенными в этом наборе: операцией сложения, записанной как a + b , и операцией умножения, записанной как a ⋅ b , обе из которых ведут себя так же, как и для рациональных и действительных чисел. , включая существование аддитивного обратного −a a всех элементов b и мультипликативного обратного для ⁻¹ для каждого ненулевого элемента b . Это позволяет также учитывать так называемые обратные операции вычитания a − b и деления a / b , определив:

а - б := а + (- б ) ,

а / б := а ⋅ б ⁻¹ .

Классическое определение

Формально поле — это множество F вместе с двумя двоичными операциями над F, называемыми сложением и умножением . Бинарная операция над F — это отображение F × F → F , то есть соответствие, которое сопоставляет каждой упорядоченной паре элементов F элемент F. однозначно определенный Результат сложения a и b называется суммой a и b и обозначается a + b . Аналогично, результат умножения a и b называется произведением a и b и обозначается ab или a ⋅ b . Эти операции необходимы для удовлетворения следующих свойств, называемых аксиомами поля (в этих аксиомах a , b и c — произвольные элементы поля F ):

• Ассоциативность сложения и умножения: a + ( b + c ) = ( a + b ) + c , и a ⋅ ( b ⋅ c ) = ( a ⋅ b ) ⋅ c .
• Коммутативность сложения и умножения: a + b = b + a и a ⋅ b = b ⋅ a .
• Аддитивное и мультипликативное тождество : существуют два различных элемента 0 и 1 в F такие, что a + 0 = a и a ⋅ 1 = a .
• Аддитивные инверсии : для каждого a в F существует элемент в F , обозначаемый , −a называемый аддитивным обратным к a , такой, что a + (− a ) = 0 .
• Мультипликативные обратные : для каждого a ≠ 0 в F существует элемент в F , обозначаемый a ⁻¹ или 1/ a , называемый мультипликативным обратным a , такой, что a ⋅ a ⁻¹ = 1 .
• Распределенность умножения на сложение: а ⋅ ( б + c ) знак равно ( а ⋅ б ) + ( а ⋅ c ) .

Эквивалентное и более краткое определение таково: поле имеет две коммутативные операции, называемые сложением и умножением; это группа добавляемая с 0 в качестве аддитивной идентичности; ненулевые элементы представляют собой группу при умножении с 1 в качестве мультипликативного тождества; и умножение распределяет над сложением.

Еще более кратко: поле — это коммутативное кольцо , где 0 ≠ 1 и все ненулевые элементы обратимы при умножении.

Альтернативное определение

Поля также можно определять разными, но эквивалентными способами. Альтернативно можно определить поле четырьмя двоичными операциями (сложение, вычитание, умножение и деление) и их необходимыми свойствами. Деление на ноль исключено по определению. Чтобы избежать кванторов существования , поля могут определяться двумя бинарными операциями (сложение и умножение), двумя унарными операциями (дающими аддитивные и мультипликативные обратные операции соответственно) и двумя нулевыми операциями (константы 0 и 1 ). Эти операции тогда подчиняются условиям, указанным выше. Избегание кванторов существования важно в конструктивной математике и вычислениях . Эквивалентно поле можно определить с помощью тех же двух двоичных операций, одной унарной операции (мультипликативной обратной) и двух (не обязательно различных) констант 1 и -1 , поскольку 0 = 1 + (-1) и - a = (- 1) а .

Примеры

Рациональные числа

Основная статья: Рациональное число

Рациональные числа широко использовались задолго до разработки концепции поля.Это числа, которые можно записать в виде дробей a / b , где a и b — целые числа , а b ≠ 0 . Аддитивная обратная такой дроби равна − a / b , а мультипликативная обратная (при условии, что a ≠ 0 ) равна b / a , что можно увидеть следующим образом:

${\frac {b}{a}}\cdot {\frac {a}{b}}={\frac {ba}{ab}}=1.$

Абстрактно необходимые аксиомы полей сводятся к стандартным свойствам рациональных чисел. Например, закон распределительности можно доказать следующим образом:

${\begin{aligned}&{\frac {a}{b}}\cdot \left({\frac {c}{d}}+{\frac {e}{f}}\right)\\[6pt]={}&{\frac {a}{b}}\cdot \left({\frac {c}{d}}\cdot {\frac {f}{f}}+{\frac {e}{f}}\cdot {\frac {d}{d}}\right)\\[6pt]={}&{\frac {a}{b}}\cdot \left({\frac {cf}{df}}+{\frac {ed}{fd}}\right)={\frac {a}{b}}\cdot {\frac {cf+ed}{df}}\\[6pt]={}&{\frac {a(cf+ed)}{bdf}}={\frac {acf}{bdf}}+{\frac {aed}{bdf}}={\frac {ac}{bd}}+{\frac {ae}{bf}}\\[6pt]={}&{\frac {a}{b}}\cdot {\frac {c}{d}}+{\frac {a}{b}}\cdot {\frac {e}{f}}.\end{aligned}}$

Действительные и комплексные числа

Умножение комплексных чисел можно визуализировать геометрически с помощью вращений и масштабирования.

Основные статьи: Действительное число и Комплексное число

Действительные числа R вместе с обычными операциями сложения и умножения также образуют поле. Комплексные числа C состоят из выражений

a + bi , где a , b вещественное,

где i — мнимая единица , т. е. (недействительное) число, удовлетворяющее i ² = −1 .Сложение и умножение действительных чисел определяются таким образом, что выражения этого типа удовлетворяют всем аксиомам поля и, следовательно, выполняются для C . Например, распределительный закон обеспечивает

( a + bi )( c + di ) = ac + bci + adi + bdi ² знак равно ( ac - bd ) + ( bc + объявление ) я .

Сразу видно, что это снова выражение вышеуказанного типа, и поэтому комплексные числа образуют поле. Комплексные числа могут быть геометрически представлены в виде точек на плоскости с декартовыми координатами , заданными действительными числами их описывающего выражения, или в виде стрелок от начала координат до этих точек, определяемых их длиной и углом, заключенным в каком-то определенном направлении. Тогда сложение соответствует объединению стрелок в интуитивно понятный параллелограмм (добавление декартовых координат), а умножение – менее интуитивно – объединяет вращение и масштабирование стрелок (сложение углов и умножение длин). Поля действительных и комплексных чисел используются в математике, физике, технике, статистике и многих других научных дисциплинах.

Конструируемые числа

Теорема о среднем геометрическом утверждает, что h ² = рк . Выбор q = 1 позволяет извлечь квадратный корень из заданного конструктивного числа p .

Основная статья: Конструируемые числа

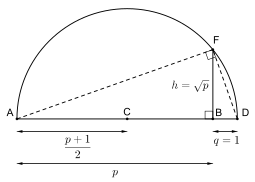
В древности несколько геометрических проблем касались (не)возможности построения определенных чисел с помощью циркуля и линейки . Например, грекам было неизвестно, что разделить данный угол таким способом вообще невозможно. Эти проблемы можно решить, используя поле конструктивных чисел . Действительные конструктивные числа — это, по определению, длины отрезков линий, которые можно построить из точек 0 и 1 за конечное число шагов, используя только циркуль и линейку . Эти числа, наделенные полевыми операциями над действительными числами, ограниченными конструктивными числами, образуют поле, которое собственно включает в себя поле Q рациональных чисел. На иллюстрации показано построение квадратных корней конструктивных чисел, не обязательно содержащихся в Q . Используя обозначения на рисунке, постройте отрезки AB , BD и полукруг над AD (центр в средней точке C ), который пересекает перпендикуляр, проходящий через B в точке F , на расстоянии ровно $h={\sqrt {p}}$ из B, когда BD имеет длину один.

Не все действительные числа конструктивны. Можно показать, что ${\sqrt[{3}]{2}}$ не является конструктивным числом, а это означает, что невозможно построить с помощью циркуля и линейки длину стороны куба объемом 2 - еще одна проблема, поставленная древними греками.

Поле с четырьмя элементами

Основная статья: Конечное поле § Поле с четырьмя элементами

Добавление	Умножение
+ ТО я А Б ТО ТО я А Б я я ТО Б А А А Б ТО я Б Б А я ТО	⋅ ТО я А Б ТО ТО ТО ТО ТО я ТО я А Б А ТО А Б я Б ТО Б я А

Помимо привычных систем счисления, таких как рациональные числа, существуют и другие, менее наглядные примеры полей. В следующем примере показано поле, состоящее из четырех элементов с O , I , A и B. именами Обозначения выбраны так, что O играет роль аддитивного тождественного элемента (обозначенного 0 в аксиомах выше), а I - мультипликативного тождества (обозначенного 1 в аксиомах выше). Аксиомы поля можно проверить, используя еще немного теории поля или путем прямых вычислений. Например,

A ⋅ ( B + A ) = A ⋅ I = A , что равно A ⋅ B + A ⋅ A = I + B = A , как того требует дистрибутивность.

Это поле называется конечным полем или полем Галуа с четырьмя элементами и обозначается F ₄ или GF(4) . Подмножество , состоящее из O и I (выделено красным в таблицах справа), также является полем, известным как двоичное поле F ₂ или GF(2) .

Элементарные понятия

В этом разделе F поле, а a и b — произвольные элементы F . обозначает произвольное

Последствия определения

Имеем a ⋅ 0 = 0 и − a = (−1) ⋅ a . В частности, можно вывести аддитивную инверсию каждого элемента, как только известно −1 .

Если ab = 0 , то a или b должно быть равно 0 , поскольку, если a ≠ 0 , то б = ( а ⁻¹ а ) б = а ⁻¹ ( аб ) = а ⁻¹ ⋅ 0 знак равно 0 . Это означает, что каждое поле является областью целостности .

справедливы следующие свойства Кроме того, для любых элементов a и b :

−0 = 0

1 ⁻¹ = 1

(−(− а )) = а

(- а ) ⋅ б знак равно а ⋅ (- б ) знак равно - ( а ⋅ б )

( а ⁻¹ ) ⁻¹ = а, если а ≠ 0

Аддитивные и мультипликативные группы поля

Из аксиом поля F следует, что оно является абелевой группой при сложении. Эта группа называется аддитивной группой поля и иногда обозначается ( F , +), поскольку ее простое обозначение F может сбить с толку.

Аналогично, ненулевые элементы F образуют абелеву группу при умножении, называемую мультипликативной группой и обозначаемую $(F\smallsetminus \{0\},\cdot )$ или просто $F\smallsetminus \{0\}$, или Ф ^× .

Таким образом, поле можно определить как множество F, оснащенное двумя операциями, называемыми сложением и умножением, так что F является абелевой группой при сложении: $F\smallsetminus \{0\}$ является абелевой группой при умножении (где 0 — единица сложения), а умножение дистрибутивно по отношению к сложению. Поэтому некоторые элементарные утверждения о полях можно получить, применяя общие факты о группах . Например, аддитивные и мультипликативные обратные — a и a ⁻¹ определяются . однозначно

Требование 1 ≠ 0 налагается по соглашению, чтобы исключить тривиальное кольцо , состоящее из одного элемента; это определяет любой выбор аксиом, определяющих поля.

Каждая конечная подгруппа мультипликативной группы поля циклическая (см. Корень из единицы § Циклические группы ).

Характеристика

В дополнение к умножению двух элементов F можно определить произведение n ⋅ a произвольного элемента a из F на положительное целое число n как n -кратную сумму

a + a + ... + a (который является элементом F .)

Если не существует такого положительного целого числа, что

п ⋅ 1 знак равно 0 ,

тогда F говорят, что имеет характеристику 0 . Например, поле рациональных чисел Q имеет характеристику 0, поскольку ни одно положительное целое число n не равно нулю. В противном случае, если существует целое положительное число n, удовлетворяющее этому уравнению, можно показать, что наименьшее такое положительное целое число является простым числом . Обычно его обозначают p , и тогда говорят, что поле имеет характеристику p .Например, поле F ₄ имеет характеристику 2 , поскольку (в обозначениях приведенной выше таблицы сложения) I + I = O .

Если F имеет характеристику p , то ⋅ a = 0 для всех a в F. p Это означает, что

( а + б ) ^п = а ^п + б ^п ,

поскольку все остальные биномиальные коэффициенты , входящие в биномиальную формулу, делятся на p . , Здесь ^п := a ⋅ a ⋅ ⋯ ⋅ a ( p множители) — это p -я степень, т. е. p -кратное произведение элемента a . Следовательно, отображение Фробениуса

F → F : x ↦ x ^п

совместим со сложением в F (а также с умножением) и, следовательно, является гомоморфизмом полей. Существование этого гомоморфизма делает поля характеристики p совершенно отличными от полей характеристики 0 .

Подполя и основные поля

Подполе E которое является поля F — это подмножество F полем относительно полевых операций F. , Эквивалентно E - это подмножество F , которое содержит 1 и замкнуто относительно сложения, умножения, аддитивного обратного и мультипликативного обратного ненулевого элемента. Это означает, что 1 ∊ E , что для всех a , b ∊ E и a + b, a ⋅ b находятся в E , и что для всех a ≠ 0 в E , оба - a и 1/ a находятся в E. и

Гомоморфизмы полей — это отображения φ : E → F между двумя полями такие, что φ ( e ₁ + e ₂ ) = φ ( e ₁ ) + φ ( e ₂ ) , φ ( e ₁ e ₂ ) = φ ( e ₁ ) φ ( e ₂ ) и φ (1 _E ) = 1 _F , где e ₁ и e ₂ — произвольные элементы из E . Все гомоморфизмы полей инъективны . Если φ также сюръективен , он называется изоморфизмом (или поля E и F называются изоморфными).

Поле называется простым, если оно не имеет собственных (т. е. строго меньших) подполей. Любое поле F содержит простое поле. Если характеристикой F является p (простое число), простое поле изоморфно конечному полю F _p, введенному ниже. В противном случае простое поле изоморфно Q .

Конечные поля

Основная статья: Конечное поле

Конечные поля (также называемые полями Галуа ) — это поля с конечным числом элементов, число которых также называется порядком поля. Приведенный выше вводный пример F ₄ представляет собой поле с четырьмя элементами. Его подполе F ₂ является наименьшим полем, поскольку по определению поле имеет как минимум два различных элемента: 0 и 1 .

В модульной арифметике по модулю 12 9 + 4 = 1, поскольку 9 + 4 = 13 в Z , что при делении на 12 оставляет остаток 1 . Однако Z /12 Z не является полем, поскольку 12 не является простым числом.

Простейшие конечные поля простого порядка наиболее легко доступны с помощью модульной арифметики . Для фиксированного положительного целого числа n арифметика «по модулю n » означает работу с числами.

Z / n Z = {0, 1, ..., n − 1}.

Сложение и умножение в этом наборе выполняются путем выполнения рассматриваемой операции в множестве Z целых чисел, деления на n и получения остатка в качестве результата. Эта конструкция дает поле именно в том случае, если n — простое число . Например, если взять простое число n = 2, получится вышеупомянутое поле F ₂ . Для n = 4 и, в более общем смысле, для любого составного числа (т. е. любого числа n , которое можно выразить как произведение n = r ⋅ s двух строго меньших натуральных чисел), Z / n Z не является полем: произведение два ненулевых элемента равны нулю, поскольку r ⋅ s = 0 в Z / n Z , что, как объяснялось выше , не позволяет Z / n Z быть полем. Поле Z / p Z с p элементами ( p — простое число), построенное таким образом, обычно обозначается F _p .

Каждое конечное поле F имеет q = p ^н элементы, где p — простое число и n ≥ 1 . Это утверждение справедливо, поскольку F можно рассматривать как векторное пространство над его простым полем. Размерность этого векторного пространства обязательно конечна, скажем, n , что и подразумевает заявленное утверждение.

Поле с q = p ^н могут быть построены как поле расщепления полинома элементы

ж ( Икс ) знак равно Икс ^д - х .

Такое поле разложения является расширением F _p, в котором многочлен f имеет q нулей. Это означает, что имеет как можно больше нулей, поскольку степень f f равна q . Для q = 2 ² = 4 , можно проверить в каждом конкретном случае, используя приведенную выше таблицу умножения, что все четыре элемента F ₄ удовлетворяют уравнению x ⁴ = x , поэтому они являются нулями f . Напротив, в F ₂ ) , f имеет только два нуля (а именно 0 и 1 поэтому f не распадается на линейные множители в этом меньшем поле. Развивая далее основные понятия теории поля, можно показать, что два конечных поля одного и того же порядка изоморфны. Поэтому принято говорить о конечном поле с q элементами, обозначаемом F _q или GF( q ) .

История

Исторически к понятию поля привели три алгебраические дисциплины: вопрос решения полиномиальных уравнений, алгебраическая теория чисел и алгебраическая геометрия . Первый шаг к понятию поля был сделан в 1770 году Жозефом -Луи Лагранжем , который заметил, что перестановка нулей x ₁ , x ₂ , x ₃ кубического многочлена в выражении

( x ₁ + ωx ₂ + ω ² х ₃ ) ³

(где ω — корень третьей степени из единицы ) дает только два значения. Таким образом, Лагранж концептуально объяснил классический метод решения Сципионе дель Ферро и Франсуа Вьета , который заключается в сведении кубического уравнения для неизвестного x к квадратному уравнению для x. ³ . Вместе с аналогичным наблюдением для уравнений четвертой степени Лагранж, таким образом, связал то, что в конечном итоге стало концепцией полей, и концепцией групп. Вандермонд , также в 1770 году, и в более полной мере Карл Фридрих Гаусс в своих Disquisitiones Arithmeticae (1801) изучили уравнение

х ^п = 1

для простого числа p и, опять же используя современный язык, полученную циклическую группу Галуа . Гаусс пришел к выводу, что правильный p -угольник можно построить, если p = 2. ^{2 к} + 1 . Основываясь на работе Лагранжа, Паоло Руффини заявил (1799), что уравнения пятой степени степени (полиномиальные уравнения 5-й ) не могут быть решены алгебраически; однако его аргументы были ошибочными. Эти пробелы были заполнены Нильсом Хенриком Абелем в 1824 году. Эварист Галуа в 1832 году разработал необходимые и достаточные критерии того, чтобы полиномиальное уравнение было алгебраически разрешимо, тем самым по сути установив то, что сегодня известно как теория Галуа . И Абель, и Галуа работали с тем, что сегодня называется полем алгебраических чисел , но не придумали ни явного понятия поля, ни группы.

В 1871 году Рихард Дедекинд ввел для обозначения набора действительных или комплексных чисел, замкнутого четырьмя арифметическими операциями, немецкое слово Körper , которое означает «тело» или «корпус» (что означает органически замкнутую сущность). Английский термин «поле» был введен Муром (1893) .

Под полем мы будем понимать всякую бесконечную систему действительных или комплексных чисел, настолько замкнутую в себе и совершенную, что сложение, вычитание, умножение и деление любых двух из этих чисел снова дает номер системы.

- Ричард Дедекинд, 1871 г.

В 1881 году Леопольд Кронекер определил то, что он назвал областью рациональности представляет собой область рациональных дробей , которая в современных терминах . Понятие Кронекера не охватывало поле всех алгебраических чисел (которое является полем в смысле Дедекинда), но, с другой стороны, было более абстрактным, чем понятие Дедекинда, поскольку оно не делало конкретных предположений о природе элементов поля. Кронекер интерпретировал такое поле, как Q (π), абстрактно как поле рациональных функций Q ( X ) . До этого примеры трансцендентных чисел были известны со времен Жозефа Лиувилля работы в 1844 году, пока Чарльз Эрмит (1873) и Фердинанд фон Линдеманн (1882) не доказали трансцендентность e и π соответственно.

Первое четкое определение абстрактного поля принадлежит Веберу (1893) . В частности, понятие Генриха Мартина Вебера включало поле F _p . Джузеппе Веронезе (1891) изучал область формальных степенных рядов, что привело Хенселя (1904) к введению области p -адических чисел. Стейниц (1910) синтезировал накопленные к настоящему времени знания абстрактной теории поля. Он аксиоматически изучил свойства полей и определил многие важные теоретико-полевые понятия. Большинство теорем, упомянутых в разделах «Теория Галуа» , «Построение полей» и «Элементарные понятия», можно найти в работах Стейница. Артин и Шрайер (1927) связали понятие упорядочения в поле и, следовательно, область анализа, с чисто алгебраическими свойствами. Эмиль Артин переработал теорию Галуа с 1928 по 1942 год, устранив зависимость от теоремы о примитивном элементе .

Создание полей

Построение полей из колец

Коммутативное кольцо — это множество, снабженное операциями сложения и умножения и удовлетворяющее всем аксиомам поля, за исключением существования мультипликативных обратных ⁻¹ . Например, целые числа Z образуют коммутативное кольцо, но не поле: обратное целое число n само по себе не является целым числом, если только n = ±1 .

В иерархии алгебраических структур поля можно охарактеризовать как коммутативные кольца R, в которых каждый ненулевой элемент является единицей (что означает, что каждый элемент обратим). , поля — это коммутативные кольца ровно с двумя различными идеалами : (0) и R. Аналогично Поля также являются коммутативными кольцами, в которых (0) является единственным простым идеалом .

Учитывая коммутативное кольцо R , есть два способа построить поле, связанное с R , т.е. два способа изменить R так, чтобы все ненулевые элементы стали обратимыми: сформировать поле частных и сформировать поля вычетов. Поле частных Z — это Q поля вычетов Z — это конечные поля Fp _. , рациональные числа, а

Поле дробей

Учитывая область целостности R , ее поле дробей Q ( R ) строится из дробей двух элементов R точно так же, как Q строится из целых чисел. Точнее, элементы Q ( R ) — это дроби a / b , где a и b находятся в R , и b ≠ 0 . Две дроби a / b и c / d равны тогда и только тогда, когда ad = bc . Операции с дробями работают точно так же, как и с рациональными числами. Например,

${\frac {a}{b}}+{\frac {c}{d}}={\frac {ad+bc}{bd}}.$

Несложно показать, что если кольцо является областью целостности, то множество дробей образует поле.

Поле F ( x ) рациональных дробей над полем (или областью целостности) F является полем частных кольца полиномов F [ x ] . Поле F (( x )) ряда Лорана

$\sum _{i=k}^{\infty }a_{i}x^{i}\ (k\in \mathbb {Z} ,a_{i}\in F)$

над полем F — поле частных кольца F [[ x ]] формальных степенных рядов (в которых k ≥ 0 ). Поскольку любой ряд Лорана представляет собой часть степенного ряда, разделенную на степень x (в отличие от произвольного степенного ряда), представление дробей в этой ситуации менее важно.

Остаточные поля

Помимо поля частных, которое вкладывает R инъективно в поле, поле можно получить из коммутативного кольца R посредством сюръективного отображения на поле F . полученное таким образом, является R / m , где m — максимальный идеал R. Любое поле , фактором Если R идеал m , это поле называется вычетов R. имеет только один максимальный полем

Идеал порожденный одним многочленом f в кольце полиномов R = E [ X ] (над полем E ), является максимальным тогда и только тогда, когда f неприводим , в E , т. е. если f не может быть выражено как произведение двух многочленов из E [ X ] меньшей степени . Это дает поле

F = E [ Икс ] / ( ж ( Икс )).

Это поле F содержит элемент x (а именно класс вычетов X ) , который удовлетворяет уравнению

ж ( Икс ) знак равно 0 .

Например, получается из R путем присоединения символа воображаемой единицы ( i , который удовлетворяет условию f ( i ) = 0 , где f C X ) = X ² + 1 . Более того, f неприводим над R , а это означает, что отображение, которое переводит многочлен f ( X ) ∊ R [ X ] в f ( i ), дает изоморфизм

$\mathbf {R} [X]/\left(X^{2}+1\right)\ {\stackrel {\cong }{\longrightarrow }}\ \mathbf {C} .$

Создание полей внутри большего поля

Поля могут быть созданы внутри заданного большего поля-контейнера. Предположим, дано поле E и поле F, содержащее E в качестве подполя. Для любого элемента x из F существует наименьшее подполе F, содержащее E и x , называемое подполем F, порожденное x и обозначаемое E ( x ) . Переход E к E ( x ) обозначается присоединением элемента к E. от В более общем смысле, для подмножества S ⊂ F существует минимальное подполе F , содержащее E и S , обозначаемое E ( S ) .

Композицией так двух подполей E и E ′ некоторого поля F является наименьшее подполе F , содержащее как E, и E ′ . Композитум можно использовать для построения самого большого подполя F, удовлетворяющего определенному свойству, например самого большого подполя , которое на языке, представленном ниже, является алгебраическим над E. F

Расширения полей

Дополнительная информация: Глоссарий теории поля.

Понятие подполя E ⊂ F можно также рассматривать с противоположной точки зрения, ссылаясь на то, что F является расширением поля (или просто расширением) поля E , обозначаемым через

Ф / Е ,

и прочитайте « F над E ».

Базовыми данными расширения поля является его степень [ F : E ] , т.е. размерность F как E -векторного пространства. Он удовлетворяет формуле

[ грамм : E ] знак равно [ грамм : F ] [ F : E ] .

Расширения, степень которых конечна, называются конечными расширениями. Расширения C / R и F ₄ / F ₂ имеют степень 2 , тогда как R / Q — бесконечное расширение.

Алгебраические расширения

Ключевым понятием в изучении расширений полей F / E являются алгебраические элементы . Элемент x ∈ F является алгебраическим над E, он является корнем многочлена если с коэффициентами из E , то есть если он удовлетворяет полиномиальному уравнению

и  х ^н + е _{н −1} х ^{п -1} + ⋯ + е ₁ Икс + е ₀ знак равно 0 ,

с e _n , ..., e ₀ в E и e _n ≠ 0 .Например, мнимая единица i в C является алгебраической над R и даже над Q , поскольку она удовлетворяет уравнению

я ² + 1 = 0 .

Расширение поля, в котором каждый элемент F является алгебраическим над E, называется алгебраическим расширением . Любое конечное расширение обязательно является алгебраическим, как можно вывести из приведенной выше формулы мультипликативности.

Подполе E ( x ), порожденное элементом x , как указано выше, является алгебраическим расширением E тогда и только тогда, когда x является алгебраическим элементом. Другими словами, если x является алгебраическим, все остальные элементы E ( x ) также обязательно являются алгебраическими. Более того, степень расширения E ( x ) / E , то есть размерность E ( x ) как E -векторного пространства, равна минимальной степени n такой, что существует полиномиальное уравнение с участием x , как указано выше. Если эта степень равна n , то элементы E ( x ) имеют вид

$\sum _{k=0}^{n-1}a_{k}x^{k},\ \ a_{k}\in E.$

Например, поле Q ( i ) гауссовских рациональных чисел — это подполе C, состоящее из всех чисел формы a + bi , где a и b — рациональные числа: слагаемые формы i ² (и аналогично для более высоких показателей) здесь рассматривать не нужно, поскольку a + bi + ci ² можно упростить до a − c + bi .

Основы трансцендентности

Упомянутое выше поле рациональных дробей E ( X ) , где X — неопределенное число , не является алгебраическим расширением E поскольку не существует полиномиального уравнения с коэффициентами из E, нулем которого является X. , Элементы, такие как X , которые не являются алгебраическими, называются трансцендентными . Неформально говоря, неопределенное X и его степени не взаимодействуют с элементами E . Аналогичное построение можно провести и с набором неопределенных, а не с одним.

Еще раз, расширение поля E ( x )/ E, обсуждавшееся выше, является ключевым примером: если x не является алгебраическим (т. е. x не является корнем многочлена с коэффициентами из E ), то E ( x ) изоморфно E ( Х ) . Этот изоморфизм получается заменой x на X в рациональных дробях.

Подмножество S поля F является базисом трансцендентности , если оно алгебраически независимо (не удовлетворяет никаким полиномиальным соотношениям) над E и если F является алгебраическим расширением E ( S ) . Любое расширение поля F / E имеет базис трансцендентности. Таким образом, расширения полей можно разделить на расширения вида E ( S )/ E ( чисто трансцендентные расширения ) и алгебраические расширения.

Операции закрытия

Поле называется алгебраически замкнутым , если оно не имеет строго больших алгебраических расширений или, что то же самое, если любое полиномиальное уравнение

ж _н   х ^н + ж _{н −1} х ^{п -1} + ⋯ + f ₁ x + f ₀ = 0 , с коэффициентами f _n , ..., f ₀ ∈ F , n > 0 ,

имеет решение x ∊ F . По основной теореме алгебры C любое алгебраически замкнуто, т. е. полиномиальное уравнение с комплексными коэффициентами имеет комплексное решение. Рациональные и действительные числа не являются алгебраически замкнутыми, поскольку уравнение

х ² + 1 = 0

не имеет никакого рационального или реального решения. Поле, содержащее F, называется алгебраическим замыканием F , если оно алгебраически над F (грубо говоря, не слишком велико по сравнению с F ) и алгебраически замкнуто (достаточно велико, чтобы содержать решения всех полиномиальных уравнений).

По вышесказанному C является алгебраическим замыканием R . Ситуация, когда алгебраическое замыкание является конечным расширением поля F, особенная: по теореме Артина–Шрайера этого расширения обязательно равна 2 , а F эквивалентно элементарно R. степень совершенно Такие поля также известны как настоящие закрытые поля .

Любое поле F имеет алгебраическое замыкание, причём единственное с точностью до (неединственного) изоморфизма. Его обычно называют алгебраическим замыканием и обозначают F . Например, алгебраическое замыкание Q поля Q называется полем алгебраических чисел . Поле F обычно довольно неявно, поскольку для его построения требуется лемма об ультрафильтре — теоретико-множественная аксиома, более слабая, чем аксиома выбора . В этом отношении алгебраическое замыкание F _q исключительно просто. Это объединение конечных полей, содержащих F _q (порядка q ^н ). Для любого алгебраически замкнутого поля F характеристики 0 алгебраическим замыканием поля F (( t )) рядов Лорана является поле рядов Пюизо , полученных присоединением корней из t .

Поля с дополнительной структурой

Поскольку поля повсеместно распространены в математике и за ее пределами, некоторые усовершенствования концепции были адаптированы к потребностям конкретных математических областей.

Упорядоченные поля

Основная статья: Упорядоченное поле

Поле F называется упорядоченным полем , если любые два элемента можно сравнить, так что x + y ≥ 0 и xy ≥ 0 всякий раз, когда x ≥ 0 и y ≥ 0 . Например, действительные числа образуют упорядоченное поле с обычным порядком ≥ . Теорема Артина -Шрайера утверждает, что поле можно упорядочить тогда и только тогда, когда оно является формально вещественным полем , а это означает, что любое квадратное уравнение

$x_{1}^{2}+x_{2}^{2}+\dots +x_{n}^{2}=0$

имеет только решение x ₁ знак равно x ₂ знак равно ⋯ знак равно x _n знак равно 0 . Множество всех возможных порядков на фиксированном поле изоморфно множеству гомоморфизмов колец из кольца Витта W( F ) квадратичных форм над F в Z. F

Архимедово поле — это упорядоченное поле, для каждого элемента которого существует конечное выражение.

1 + 1 + ⋯ + 1

значение которого больше этого элемента, то есть бесконечных элементов не существует. Эквивалентно, поле не содержит бесконечно малых (элементов, меньших всех рациональных чисел); или, что эквивалентно, поле изоморфно подполю R .

Каждое ограниченное вещественное множество имеет наименьшую верхнюю границу.

Упорядоченное поле является дедекинд-полным, если все верхние границы , нижние границы (см. Дедекиндов разрез ) и пределы, которые должны существовать, существуют. Более формально, каждое ограниченное подмножество должно F иметь наименьшую верхнюю границу. Любое полное поле обязательно архимедово, поскольку в любом неархимедовом поле не существует ни наибольшего бесконечно малого, ни наименьшего положительного рационального, следовательно, последовательность 1/2, 1/3, 1/4,... , каждый элемент которой больше всех бесконечно малых, не имеет предел.

Поскольку каждое собственное подполе вещественных чисел также содержит такие пробелы, R — единственное полное упорядоченное поле с точностью до изоморфизма. Некоторые основополагающие результаты в исчислении непосредственно следуют из этой характеристики действительности.

Гиперреалии ​ R ^* образуют упорядоченное поле, не являющееся архимедовым. Это расширение действительных чисел, полученное путем включения бесконечных и бесконечно малых чисел. Они больше и соответственно меньше любого действительного числа. Гиперреалы составляют фундаментальную основу нестандартного анализа .

Топологические поля

Еще одним уточнением понятия поля является топологическое поле , в котором множество F является топологическим пространством , таким, что все операции поля (сложение, умножение, отображения a ↦ − a и a ↦ a ⁻¹ ) являются непрерывными отображениями относительно топологии пространства. Топология всех обсуждаемых ниже полей индуцируется метрикой , т. е . функцией

г : F × F → р ,

который измеряет расстояние между любыми двумя элементами F .

Пополнение — F F «пробелы» в исходном поле , это еще одно поле, в котором, неформально говоря, заполняются если таковые имеются. Например, любое иррациональное число x , такое как x = √ 2 , является «пробелом» в рациональных числах Q в том смысле, что это действительное число, которое можно сколь угодно близко аппроксимировать рациональными числами p / q , в том смысле, что расстояние x и p / q, заданное абсолютным значением | Икс - п / д | настолько мал, насколько хотелось бы.В следующей таблице приведены некоторые примеры этой конструкции. В четвертом столбце показан пример нулевой последовательности , т. е. последовательности, предел которой (при n → ∞ ) равен нулю.

Поле	Метрика	Завершение	нулевая последовательность
вопрос	| х - у | (обычное абсолютное значение )	Р	1/ н
вопрос	полученное с использованием p -адической оценки для простого числа p	Q p ( p -адические числа )	п н
Ф ( т ) ( F любое поле)	полученное с использованием t -адической оценки	Ф (( т ))	т н

Поле Qp _p используется в теории чисел и - адическом анализе . Алгебраическое замыкание Qp _{имеет единственную норму ,} расширяющую норму на Qp _, но не является полным. Однако пополнение этого алгебраического замыкания алгебраически замкнуто. Из-за грубой аналогии с комплексными числами его иногда называют полем комплексных p -адических чисел и обозначают C _p .

Локальные поля

Следующие топологические поля называются локальными полями :

• конечные расширения Q _p (локальные поля нулевой характеристики)
• конечные расширения F _p (( t )) , поля рядов Лорана над F _p (локальные поля характеристики p ).

Эти два типа локальных полей имеют некоторые фундаментальные сходства. В этом отношении элементы p ∈ Q _p и t ∈ F _p (( t )) (называемые униформизатором ) соответствуют друг другу. Первое проявление этого находится на элементарном уровне: элементы обоих полей могут быть выражены в виде степенных рядов в униформизаторе с коэффициентами в F _p . (Однако, поскольку сложение в Q _p осуществляется с использованием переноса , чего не происходит в F _p (( t )) эти поля не изоморфны.) Следующие факты показывают, что это поверхностное сходство идет гораздо глубже:

• Любое утверждение первого порядка , верное почти для всех Q _p, также верно для почти всех F _p (( t )) . Приложением этого является теорема Аха–Кохена, описывающая нули однородных многочленов в Q _p .
• Укрощенно разветвленные расширения обоих полей биекционны друг другу.
• Присоединение произвольных p p-степени из ( в Qp ₎ , соответственно, из t (в Fp _корней (( t ) ) дает (бесконечные) расширения этих полей, известные как перфектоидные поля . Поразительно, но группы Галуа этих двух полей изоморфны, что является первым проблеском замечательной параллели между этими двумя полями:
  $$\operatorname {Gal} \left(\mathbf {Q} _{p}\left(p^{1/p^{\infty }}\right)\right)\cong \operatorname {Gal} \left(\mathbf {F} _{p}((t))\left(t^{1/p^{\infty }}\right)\right).$$

Дифференциальные поля

Дифференциальные поля — это поля, снабженные дифференцированием , т. е. позволяющие брать производные элементов поля. Например, поле R ( X ) вместе со стандартной производной многочленов образует дифференциальное поле. Эти поля являются центральными в дифференциальной теории Галуа , варианте теории Галуа, занимающейся линейными дифференциальными уравнениями .

Теория Галуа

Основная статья: теория Галуа

Теория Галуа изучает алгебраические расширения поля путем изучения симметрии арифметических операций сложения и умножения. Важным понятием в этой области является понятие конечных расширений Галуа F / E , которые по определению являются сепарабельными и нормальными . Теорема о примитивном элементе показывает, что конечные сепарабельные расширения обязательно просты , т. е. имеют вид

F знак равно E [ Икс ] / ж ( Икс ) ,

где f — неприводимый полином (как указано выше). Для такого расширения нормальность и сепарабельность означает, что все нули f содержатся в F и что f имеет только простые нули. Последнее условие всегда выполняется, если E имеет характеристику 0 .

Для конечного расширения Галуа группа Галуа Gal( F / E ) — это группа полевых автоморфизмов F F , которые тривиальны на E (т. е. биекции σ : F → , которые сохраняют сложение и умножение и которые переводят элементы E в сами себя). Важность этой группы вытекает из фундаментальной теоремы теории Галуа , которая строит явное взаимно однозначное соответствие между множеством подгрупп Gal ( F / E ) и множеством промежуточных расширений расширения F / E . Посредством этого соответствия теоретико-групповые свойства преобразуются в факты о полях. Например, если группа Галуа расширения Галуа, как указано выше, неразрешима ( не может быть построена из абелевых групп ), то нули f не могут быть выражены через сложение, умножение и радикалы, т. е. выражения, включающие ${\sqrt[{n}]{~}}$. Например, симметрические группы Sn _n неразрешимы при ≥ 5 . Следовательно, как можно показать, нули следующих многочленов не выражаются через суммы, произведения и радикалы. Для последнего многочлена этот факт известен как теорема Абеля – Руффини :

ж ( Икс ) знак равно Икс ⁵ − 4 X + 2 (и E = Q ),

ж ( Икс ) знак равно Икс ^н + а _{n −1} X ^{п -1} + ⋯ + a ₀ (где f рассматривается как полином от E ( a ₀ , ..., a _{n −1} ) , для некоторых неопределенных a _i , E - любое поле и n ≥ 5 ).

Тензорное произведение полей обычно не является полем. Например, конечное расширение F / E степени n является расширением Галуа тогда и только тогда, когда существует изоморфизм F -алгебр

Ф ⊗ _Е Ф ≅ Ф ^н .

Этот факт является началом теории Галуа Гротендика , далеко идущего расширения теории Галуа, применимого к алгебро-геометрическим объектам.

Инварианты полей

Основные инварианты поля F включают характеристику и степень трансцендентности поля F над его простым полем. Последнее определяется как максимальное число элементов в F , алгебраически независимых над простым полем. Два алгебраически замкнутых поля E и F изоморфны именно в том случае, если эти два данных совпадают. Отсюда следует, что любые два несчетных алгебраически замкнутых поля одинаковой мощности и одной характеристики изоморфны. Например, Qp _не , Cp _и как C изоморфны (но изоморфны топологические поля).

Модельная теория полей

В теории моделей , разделе математической логики , два поля E и F называются элементарно эквивалентными, если каждое математическое утверждение, верное для E , также верно и для F , и наоборот. Рассматриваемые математические утверждения должны быть предложениями первого порядка (включая 0 , 1 , сложение и умножение). Типичный пример для n > 0 , n — целое число:

φ ( E ) = "любой многочлен степени n из E имеет нуль в E "

Набор таких формул для всех n выражает E. алгебраическую замкнутость Принцип Лефшеца утверждает, что C элементарно эквивалентно любому алгебраически замкнутому полю F нулевой характеристики. Более того, любое фиксированное утверждение φ выполняется в C тогда и только тогда, когда оно выполняется в любом алгебраически замкнутом поле достаточно высокой характеристики.

Если U — ультрафильтр множестве I , а F _i — поле для каждого i в I , ультрапроизведение F i _на относительно U является полем. Это обозначается

ulim _{i →∞} F _i ,

поскольку оно во многих отношениях ведет себя как предел полей Fi _{утверждает, что любое утверждение первого порядка ,} : теорема Лоша справедливое для всех, кроме конечного числа Fi _, также верно и для ультрапроизведения. Применительно к приведенному выше предложению φ это показывает, что существует изоморфизм

$\operatorname {ulim} _{p\to \infty }{\overline {\mathbf {F} }}_{p}\cong \mathbf {C} .$

Отсюда также следует упомянутая выше теорема Аха–Кохена и изоморфизм ультрапроизведений (в обоих случаях по всем простым числам p )

улим _п Q _п ≅ улим _п F _п (( т )) .

Кроме того, теория моделей также изучает логические свойства различных других типов полей, таких как реальные замкнутые поля или экспоненциальные поля (которые оснащены показательной функцией exp : F → F ^× ).

Абсолютная

Для полей, которые не являются алгебраически замкнутыми (или не сепарабельно замкнутыми), абсолютная группа Галуа Gal( F ) имеет фундаментальное значение: расширяя случай конечных расширений Галуа, описанный выше, эта группа управляет всеми конечными сепарабельными расширениями F . , что группа ( F _q ) можно показать является группой Прюфера , проконечным пополнением Z. Gal Элементарными средствами Это утверждение учитывает тот факт, что единственными алгебраическими расширениями Gal( F _q ) являются поля Gal( F _{q ^н} ) для n > 0 и что группы Галуа этих конечных расширений имеют вид

Гал( F _{q ^н} / F _q ) знак равно Z / п Z .

Описание в терминах образующих и соотношений известно также для групп Галуа p -адических чисел (конечных расширений Qp _полей ).

Представления групп Галуа и родственных групп, таких как группа Вейля, являются фундаментальными во многих разделах арифметики, таких как программа Ленглендса . Когомологическое исследование таких представлений проводится с использованием когомологий Галуа . Например, группу Брауэра , которая классически определяется как группа центральных простых F -алгебр , можно переинтерпретировать как группу когомологий Галуа, а именно

Бр( F ) = Ч ² ( F , G _м ) .

К-теория

К-теория Милнора определяется как

$K_{n}^{M}(F)=F^{\times }\otimes \cdots \otimes F^{\times }/\left\langle x\otimes (1-x)\mid x\in F\smallsetminus \{0,1\}\right\rangle .$

Теорема об изоморфизме норм вычетов , доказанная около 2000 года Владимиром Воеводским , связывает это с когомологиями Галуа посредством изоморфизма.

$K_{n}^{M}(F)/p=H^{n}(F,\mu _{l}^{\otimes n}).$

Алгебраическая К-теория связана с группой обратимых матриц с коэффициентами данного поля. Например, процесс взятия определителя обратимой матрицы приводит к изоморфизму K ₁ ( F ) = F ^× . Теорема Мацумото показывает, что K ₂ ( F ) согласуется с K ₂ ^М ( Ф ) . В более высоких степенях К-теория расходится с К-теорией Милнора и в целом остается трудновычислимой.

Приложения

Линейная алгебра

Если a ≠ 0 , то уравнение

топор = б

имеет единственное решение x в поле F , а именно $x=a^{-1}b.$ Это непосредственное следствие определения поля является фундаментальным в линейной алгебре . Например, это важный компонент метода исключения Гаусса и доказательства того, что любое векторное пространство имеет базис .

Теория модулей (аналог векторных пространств над кольцами вместо полей) гораздо сложнее, поскольку приведенное выше уравнение может иметь несколько решений или не иметь их. В частности, системы линейных уравнений над кольцом решать гораздо труднее, чем в случае полей, даже в особенно простом случае кольца Z целых чисел.

поля: криптография и

Сумма трех точек P , Q и R на эллиптической кривой E (красная) равна нулю, если через эти точки проходит линия (синяя).

Широко применяемая криптографическая процедура использует тот факт, что дискретное возведение в степень, т. е. вычисление

а ^н знак равно а ⋅ а ⋅ ⋯ ⋅ а ( n множителей, для целого числа n ≥ 1 )

в (большом) конечном поле F _q может выполняться гораздо эффективнее, чем дискретный логарифм , который является обратной операцией, т. е. определением решения n уравнения

а ^н = б .

В криптографии эллиптических кривых умножение в конечном поле заменяется операцией сложения точек на эллиптической кривой , т. е. решений уравнения вида

и ² = х ³ + топор + б .

Конечные поля также используются в теории кодирования и комбинаторике .

Геометрия: поле функций

Компактная риманова поверхность рода два (две ручки). Род можно определить по полю мероморфных функций на поверхности.

Функции в подходящем топологическом пространстве X в поле F можно складывать и умножать поточечно, например, произведение двух функций определяется произведением их значений внутри области:

( ж ⋅ г )( Икс ) знак равно ж ( Икс ) ⋅ г ( Икс ) .

Это делает эти функции F - коммутативной алгеброй .

Чтобы иметь поле функций, необходимо рассматривать алгебры функций, которые являются областью целостности . В этом случае отношения двух функций, т. е. выражения вида

${\frac {f(x)}{g(x)}},$

образуют поле, называемое полем функций.

Это происходит в двух основных случаях. Когда X — многообразие X. комплексное В этом случае рассматривается алгебра голоморфных функций , т. е. комплексно дифференцируемых функций. Их отношения образуют поле функций на X. мероморфных

Поле функций алгебраического многообразия X (геометрический объект, определяемый как общие нули полиномиальных уравнений) состоит из отношений регулярных функций , т. е. отношений полиномиальных функций на многообразии. Функциональное поле n -мерного пространства полем F есть F ( x1 _n ,..., xn _над ) , т. е. поле, состоящее из отношений многочленов от неопределенных значений. Функциональное поле X такое же, как и у любого открытого плотного подмногообразия. Другими словами, функциональное поле нечувствительно к замене X на (немного) меньшее подмногообразие.

Поле функций инвариантно относительно изоморфизма и бирациональной эквивалентности многообразий. Поэтому это важный инструмент для изучения абстрактных алгебраических многообразий и классификации алгебраических многообразий. Например, размерность , равная степени трансцендентности F ( X ) , инвариантна относительно бирациональной эквивалентности. Для кривых т. е. размерность равна единице) функциональное поле F ( X ) очень близко к X : если X гладкое ( и собственное (аналог компактности ) , X можно восстановить с точностью до изоморфизма по его полю функций. В более высоком измерении функциональное поле запоминает меньшую, но все же решающую информацию X. о Изучение функциональных полей и их геометрического смысла в высших измерениях называется бирациональной геометрией . Программа минимальной модели пытается идентифицировать простейшие (в определенном точном смысле) алгебраические многообразия с заданным функциональным полем.

: глобальные

Глобальные поля находятся в центре внимания алгебраической теории чисел и арифметической геометрии .Они, по определению, являются числовыми полями (конечными расширениями Q ) или функциональными полями над F _q (конечными расширениями F _q ( t ) ). Что касается локальных полей, то эти два типа полей имеют несколько схожих особенностей, хотя они имеют характеристику 0 и положительную характеристику соответственно. Эта аналогия с функциональным полем может помочь сформировать математические ожидания, часто сначала путем понимания вопросов о функциональных полях, а затем рассмотрения случая числового поля. Последнее зачастую сложнее. Например, гипотезу Римана о нулях дзета-функции Римана (открытую по состоянию на 2017 год) можно рассматривать как параллельную гипотезе Вейля (доказанной в 1974 году Пьером Делинем ).

Пятые корни из единицы образуют правильный пятиугольник .

Циклотомические поля являются одними из наиболее интенсивно изучаемых числовых полей. Они имеют вид Q ( ζ _n ) , где ζ _n — примитивный корень n-й степени из единицы , т. е. комплексное число ζ , удовлетворяющее условию ζ ^н = 1 и ζ ^м ≠ 1 для всех 0 < m < n . Поскольку n является обычным простым числом , Куммер использовал круговые поля для доказательства Великой теоремы Ферма , которая утверждает отсутствие рациональных ненулевых решений уравнения

х ^н + и ^н = г ^н .

Локальные поля являются дополнениями глобальных полей. Теорема Островского утверждает, что единственными пополнениями глобального поля Q являются локальные поля Q _p и R . Изучение арифметических вопросов в глобальных полях иногда можно проводить, рассматривая соответствующие вопросы локально. Этот метод называется локально-глобальным принципом . Например, теорема Хассе–Минковского сводит задачу поиска рациональных решений квадратных уравнений к решению этих уравнений в и Qp , _R решения которых легко описать.

В отличие от локальных полей, группы Галуа глобальных полей неизвестны. Обратная теория Галуа является ли какая-либо конечная группа группой Галуа Gal( F / Q ) для некоторого числового поля F. изучает (нерешенную) проблему , Теория полей классов описывает абелевы расширения , т. е. расширения с абелевой группой Галуа или, что то же самое, абелианизированные группы Галуа глобальных полей. Классическое утверждение, теорема Кронекера–Вебера , описывает максимальный абелиан Q ^аб расширение Q : это поле

Q ( ζ _n , n ≥ 2)

получается присоединением всех примитивных корней n -й степени из единицы. «Югендтраум» Кронекера требует столь же подробного описания F. ^аб общих числовых полей F . Для мнимых квадратичных полей $F=\mathbf {Q} ({\sqrt {-d}})$, d > 0 , теория комплексного умножения описывает F ^аб с помощью эллиптических кривых . Для общих числовых полей такое явное описание не известно.

Связанные понятия

Помимо дополнительной структуры, которой могут обладать поля, поля допускают различные другие связанные понятия. Поскольку в любом поле 0 ≠ 1 любое поле имеет как минимум два элемента. Тем не менее, существует понятие поля с одним элементом , которое предлагается считать пределом конечных полей F _p , поскольку p стремится к 1 . Помимо тел, существуют различные другие более слабые алгебраические структуры, связанные с полями, такие как квазиполя , околополя и полуполя .

Существуют также собственные классы со структурой полей, которые иногда называют Fields с заглавной буквы «F». Сюрреалистические числа образуют Поле, содержащее действительные числа, и были бы полем, если бы не тот факт, что они представляют собой собственный класс, а не набор. Нимберы теории , концепция из игр , также образуют такое Поле.

Разделительные кольца

Отказ от одной или нескольких аксиом в определении поля приводит к другим алгебраическим структурам. Как упоминалось выше, коммутативные кольца удовлетворяют всем аксиомам поля, за исключением существования мультипликативных обратных. Отказ от коммутативности умножения приводит к понятию тела или тела ; иногда ослабляется и ассоциативность. Единственными телами, которые являются конечномерными R -векторными пространствами, являются само R , C (который является полем) и кватернионы H (в которых умножение некоммутативно). Этот результат известен как теорема Фробениуса . Октонионы , для которых умножение не является ни коммутативным, ни O ассоциативным, являются нормированной альтернативной алгеброй с телом, но не телом. Этот факт был доказан методами алгебраической топологии в 1958 году Мишелем Кервером , Раулем Боттом и Джоном Милнором .

Ссылки

• Адамсон, ИТ (2007), Введение в теорию поля , Dover Publications, ISBN  978-0-486-46266-0
• Алленби, RBJT (1991), Кольца, поля и группы , Баттерворт-Хейнеманн, ISBN  978-0-340-54440-2
• Артин, Майкл (1991), Алгебра , Прентис Холл , ISBN  978-0-13-004763-2 , особенно глава 13
• Артин, Эмиль ; Шрайер, Отто (1927), «Идентификация действительно закрытых тел», статьи Математического семинара Гамбургского университета (на немецком языке), 5 : 225–231, doi : 10.1007/BF02952522 , ISSN   0025-5858 , JFM   53.0144.01 , S2CID   121547404
• Акс, Джеймс (1968), «Элементарная теория конечных полей», Ann. математики. , 2, 88 (2): 239–271, номер документа : 10.2307/1970573 , JSTOR   1970573.
• Баэз, Джон К. (2002), «Октонионы», Бюллетень Американского математического общества , 39 (2): 145–205, arXiv : math/0105155 , doi : 10.1090/S0273-0979-01-00934-X , S2CID   586512
• Банашевский, Бернхард (1992), «Алгебраическое замыкание без выбора», Z. Math. Logik Grundlagen Math. , 38 (4): 383–385, doi : 10.1002/malq.19920380136 , Zbl   0739.03027
• Бичи, Джон. А; Блер, Уильям Д. (2006), Абстрактная алгебра (3-е изд.), Waveland Press, ISBN  1-57766-443-4
• Блит, Т.С.; Робертсон, Э. Ф. (1985), Группы, кольца и поля: алгебра на практике , издательство Кембриджского университета . См. особенно Книгу 3 ( ISBN   0-521-27288-2 ) и Книга 6 ( ISBN   0-521-27291-2 ).
• Борсо, Фрэнсис; Джанелидзе, Джордж (2001), теории Галуа , Cambridge University Press, ISBN  0-521-80309-8 , Збл   0978.12004
• Бурбаки, Николя (1994), Элементы истории математики , Springer, doi : 10.1007/978-3-642-61693-8 , ISBN  3-540-19376-6 , МР   1290116
• Бурбаки, Николя (1988), Алгебра II. Главы 4–7 , Springer, ISBN  0-387-19375-8
• Кассельс, JWS (1986), Локальные поля , Студенческие тексты Лондонского математического общества, том. 3, Издательство Кембриджского университета, номер документа : 10.1017/CBO9781139171885 , ISBN.  0-521-30484-9 , МР   0861410
• Кларк, А. (1984), Элементы абстрактной алгебры , серия Dover Books on Mathematics, Dover, ISBN  978-0-486-64725-8
• Конвей, Джон Хортон (1976), О числах и играх , Academic Press
• Корри, Лео (2004), Современная алгебра и возникновение математических структур (2-е изд.), Биркхойзер, ISBN  3-7643-7002-5 , ЗБЛ   1044.01008
• Дирихле, Питер Густав Лежен (1871), Дедекинд, Рихард (редактор), Лекции по теории чисел (на немецком языке), том. 1 (2-е изд.), Брауншвейг, Германия: Фридрих Видег и сын
• Эйзенбуд, Дэвид (1995), Коммутативная алгебра с точки зрения алгебраической геометрии , Тексты для аспирантов по математике , том. 150, Нью-Йорк: Springer-Verlag , номер домена : 10.1007/978-1-4612-5350-1 , ISBN.  0-387-94268-8 , МР   1322960
• Эскофье, JP (2012), Теория Галуа , Springer, ISBN  978-1-4613-0191-2
• Фрэли, Джон Б. (1976), Первый курс абстрактной алгебры (2-е изд.), Чтение: Аддисон-Уэсли , ISBN  0-201-01984-1
• Фрике, Роберт ; Вебер, Генрих Мартин (1924), Учебник алгебры (на немецком языке), Vieweg, JFM   50.0042.03
• Гувеа, Фернандо К. (1997), p -адические числа , Universitext (2-е изд.), Springer
• Гувеа, Фернандо К. (2012), Путеводитель по группам, кольцам и полям , Математическая ассоциация Америки, ISBN  978-0-88385-355-9
• «Поле» , Энциклопедия математики , EMS Press , 2001 [1994]
• Хензель, Курт (1904), «О новом обосновании теории алгебраических чисел» , Журнал чистой и прикладной математики (на немецком языке), 128 : 1–32, ISSN   0075-4102 , JFM   35.0227.01
• Джейкобсон, Натан (2009), Основная алгебра , том. 1 (2-е изд.), Дувр, ISBN  978-0-486-47189-1
• Яннсен, Уве; Вингберг, Кей (1982), «Структура абсолютной группы Галуа трехадических числовых полей. [Структура абсолютной группы Галуа трехадических числовых полей]» , Инвент. Математика. , 70 71–98, Bibcode : 1982InMat..70...71J , doi : 10.1007/ , MR0679774   (1) : , S2CID119378923   bf01393199
• Кляйнер, Израиль (2007), Кляйнер, Израиль (редактор), История абстрактной алгебры , Биркхойзер, doi : 10.1007/978-0-8176-4685-1 , ISBN  978-0-8176-4684-4 , МР   2347309
• Кирнан, Б. Мелвин (1971), «Развитие теории Галуа от Лагранжа до Артена», Архив истории точных наук , 8 (1–2): 40–154, doi : 10.1007/BF00327219 , MR   1554154 , S2CID   121442989
• Кульманн, Сальма (2000), Упорядоченные экспоненциальные поля , Монографии Института Поля, том. 12, Американское математическое общество, ISBN.  0-8218-0943-1 , МР   1760173
• Ланг, Серж (2002), Алгебра , Тексты для выпускников по математике, том. 211 (3-е изд.), Springer, номер документа : 10.1007/978-1-4613-0041-0 , ISBN.  0-387-95385-Х
• Лидл, Рудольф; Нидеррайтер, Харальд (2008), Конечные поля (2-е изд.), Cambridge University Press, ISBN  978-0-521-06567-2 , Збл   1139.11053
• Лоренц, Фалько (2008), Алгебра, Том II: Поля со структурами, алгебры и дополнительные темы , Springer, ISBN  978-0-387-72487-4
• Маркер, Дэвид; Мессмер, Маргит; Пиллэй, Ананд (2006), Модельная теория полей , Конспект лекций по логике, том. 5 (2-е изд.), Ассоциация символической логики, CiteSeerX   10.1.1.36.8448 , ISBN  978-1-56881-282-3 , МР   2215060
• Маккой, Нил Х. (1968), Введение в современную алгебру, исправленное издание , Бостон: Аллин и Бэкон , LCCN   68015225
• Майнс, Рэй; Ричман, Фред; Рюйтенбург, Вим (1988), Курс конструктивной алгебры , Universitext, Springer, doi : 10.1007/978-1-4419-8640-5 , ISBN  0-387-96640-4 МР  0919949
• Мур, Э. Гастингс (1893), «Дважды бесконечная система простых групп», Бюллетень Американского математического общества , 3 (3): 73–78, doi : 10.1090/S0002-9904-1893-00178-X , МР   1557275
• Престель, Александр (1984), Лекции по формально действительным полям , Конспекты лекций по математике, том. 1093, Спрингер, номер домена : 10.1007/BFb0101548 , ISBN.  3-540-13885-4 , МР   0769847
• Рибенбойм, Пауло (1999), Теория классических оценок , Монографии Springer по математике , Springer, doi : 10.1007/978-1-4612-0551-7 , ISBN  0-387-98525-5 , МР   1677964
• Шольце, Питер (2014), «Перфектоидные пространства и их приложения» (PDF) , Труды Международного конгресса математиков 2014 г. , Кён Мун SA, ISBN  978-89-6105-804-9
• Схоутенс, Ганс (2002), Использование ультрапроизведений в коммутативной алгебре , Конспект лекций по математике, том. 1999, Спрингер, ISBN  978-3-642-13367-1
• Серр, Жан-Пьер (1996) [1978], Курс арифметики. Перевод Cours d'arithmetique , Текст для выпускников по математике, том. 7 (2-е изд.), Springer, ISBN  9780387900407 , Збл   0432.10001
• Серр, Жан-Пьер (1979), Местные поля , Тексты для выпускников по математике, том. 67, Спрингер, ISBN  0-387-90424-7 , МР   0554237
• Серр, Жан-Пьер (1992), Темы теории Галуа , Jones and Bartlett Publishers, ISBN  0-86720-210-6 , Збл   0746.12001
• Серр, Жан-Пьер (2002), Когомологии Галуа , Монографии Спрингера по математике, перевод с французского Патрика Иона , Берлин, Нью-Йорк: Springer-Verlag , ISBN  978-3-540-42192-4 , МР   1867431 , Збл   1004.12003
• Шарп, Дэвид (1987), Кольца и факторизация , Cambridge University Press, ISBN  0-521-33718-6 , Збл   0674.13008
• Стейниц, Эрнст (1910), «Алгебраическая теория полей», Журнал чистой и прикладной математики , 1910 (137): 167–309, doi : 10.1515/crll.1910.137.167 , ISSN   0075-4102 , JFM   41.0445.03 , S2CID   120807300
• Титс, Жак (1957), «Об алгебраических аналогах комплексных полупростых групп», Конференция по высшей алгебре, проходившая в Брюсселе с 19 по 22 декабря 1956 года, Бельгийский центр математических исследований Établissements Ceuterick, Лувен , Париж: Librairie Gauthier - Виллар, стр. 261–289
• ван дер Пут, М.; Сингер, М.Ф. (2003), Теория Галуа линейных дифференциальных уравнений , Основы математических наук, том. 328, джемпер
• фон Штаудт, Карл Георг Кристиан (1857), Вклад в геометрию положения , том. 2, Нюрнберг (Германия): Бауэр и Распе
• Уоллес, DAR (1998), Группы, кольца и поля , SUMS, vol. 151, Спрингер
• Уорнер, Сет (1989), Топологические поля , Северная Голландия, ISBN  0-444-87429-1 , Збл   0683.12014
• Вашингтон, Лоуренс К. (1997), Введение в циклотомные поля , Тексты для аспирантов по математике, том. 83 (2-е изд.), Springer-Verlag, номер документа : 10.1007/978-1-4612-1934-7 , ISBN.  0-387-94762-0 , МР   1421575
• Вебер, Генрих (1893), «Общие основы теории уравнений Галуа» , Mathematical Annals (на немецком языке), 43 (4): 521–549, doi : 10.1007/BF01446451 , ISSN   0025-5831 , JFM   25.0137.01 , S2CID   120528969