Моноид
| Алгебраические структуры |
|---|

В абстрактной алгебре , разделе математики , моноид — это множество, снабженное ассоциативной бинарной операцией и единичным элементом . Например, неотрицательные целые числа после сложения образуют моноид, единичный элемент которого равен 0 .
Моноиды — это полугруппы с единицей. Такие алгебраические структуры встречаются в нескольких разделах математики.
Функции из множества в себя образуют моноид относительно композиции функций. В более общем смысле, в теории категорий морфизмы объекта самому себе образуют моноид, и, наоборот, моноид можно рассматривать как категорию с одним объектом.
В информатике и компьютерном программировании набор строк, построенный из заданного набора символов, представляет собой свободный моноид . Моноиды переходов и синтаксические моноиды используются при описании конечных автоматов . Моноиды трассировки и моноиды истории обеспечивают основу для вычислений процессов и параллельных вычислений .
В теоретической информатике изучение моноидов является фундаментальным для теории автоматов ( теория Крона–Родса ) и теории формального языка ( проблема высоты звезды ).
См. полугруппу , чтобы узнать об истории предмета и некоторых других общих свойствах моноидов.
Определение [ править ]
Множество оснащенное S, бинарной операцией S × S → S , которую мы обозначим • , является моноидом , если оно удовлетворяет следующим двум аксиомам:
- Ассоциативность
- Для всех a , b и c в S справедливо уравнение ( a • b ) • c = a • ( b • c ) .
- Элемент идентификации
- Существует элемент e в S такой, что для каждого элемента a в S выполняются равенства e • a = a и a • e = a .
Другими словами, моноид — это полугруппа с единицей . Ее также можно рассматривать как магму, обладающую ассоциативностью и идентичностью. Единичный элемент моноида уникален. [а] По этой причине тождество рассматривается как константа , т.е. 0 -арная (или нулевая) операция. Таким образом, моноид характеризуется спецификацией тройки ( S , •, e ) .
В зависимости от контекста символ бинарной операции может быть опущен, так что операция обозначается сопоставлением ; например, аксиомы моноида могут быть записаны ( ab ) c = a ( bc ) и ea = ae = a . Это обозначение не означает, что речь идет об умножении чисел.
Моноид, в котором каждый элемент имеет обратный, является группой .
Моноидные структуры [ править ]
Субмоноиды [ править ]
Субмоноид подмножество моноида ( M , •) — это N из M , замкнутое относительно операции моноида и содержащее единичный элемент e из M . [1] [б] Символически N является субмоноидом M, если e ∈ N ⊆ M и x • y ∈ N всякий раз, x , y ∈ N. когда В этом случае N является моноидом относительно бинарной операции, унаследованной от M .
С другой стороны, если N является подмножеством моноида, замкнутого относительно операции моноида, и является моноидом для этой унаследованной операции, то N не всегда является субмоноидом, поскольку единичные элементы могут различаться. Например, одноэлементное множество {0} замкнуто при умножении и не является субмоноидом (мультипликативного) моноида неотрицательных целых чисел .
Генераторы [ править ]
подмножество S множества M Говорят, что порождает M , если наименьший подмоноид M , содержащий S, есть M . Если существует конечное множество, порождающее M , то M называется конечно порожденным моноидом .
Коммутативный моноид [ править ]
Моноид, операция которого коммутативна, называется коммутативным моноидом (или, реже, абелевым моноидом ). Коммутативные моноиды часто записываются аддитивно. Любой коммутативный моноид наделен своим алгебраическим предварительным порядком ≤ , определяемым x ≤ y , если существует z такой, что x + z = y . [2] Порядковая единица коммутативного моноида M — это элемент u из M такой, что для любого элемента x из M существует v в множестве, порожденном u, такой, что x ⩽ v . Это часто используется в случае, если M — положительный конус G частично упорядоченной абелевой группы , в этом случае мы говорим, что u — единица порядка G. и
Частично коммутативный моноид
Моноид, для которого операция коммутативна для некоторых, но не для всех элементов, является моноидом следа ; Моноиды трасс обычно встречаются в теории параллельных вычислений .
Примеры [ править ]
- Из 16 возможных бинарных логических операторов четыре имеют двустороннюю идентичность, которая также является коммутативной и ассоциативной. Каждый из этих четырех делает набор {False, True} коммутативным моноидом. Согласно стандартным определениям, AND и XNOR имеют идентификатор True , а XOR и OR имеют идентификатор False . Моноиды от AND и OR также идемпотентны , а моноиды от XOR и XNOR — нет.
- Множество натуральных чисел N = {0, 1, 2, ...} является коммутативным моноидом при сложении (единичный элемент 0 ) или умножении (единичный элемент 1 ). Субмоноид числа N при сложении называется числовым моноидом .
- Множество натуральных чисел N ∖ {0} является коммутативным моноидом относительно умножения (единичный элемент 1 ).
- Учитывая набор A , набор подмножеств A является коммутативным моноидом при пересечении (единичный элемент - это сам A ).
- Учитывая набор A , набор подмножеств A является коммутативным моноидом при объединении (единичный элемент - это пустое множество ).
- Обобщая предыдущий пример, каждая ограниченная полурешетка является идемпотентным коммутативным моноидом.
- В частности, любая ограниченная решетка может иметь как структуру моноида , так и структуру соединения . Элементами идентичности являются верх и низ решетки соответственно. Будучи решетками, гейтинговы алгебры и булевы алгебры наделены этими моноидными структурами.
- Каждое одноэлементное множество { x }, замкнутое относительно бинарной операции, • образует тривиальный (одноэлементный) моноид, который также является тривиальной группой .
- Каждая группа является моноидом, а каждая абелева группа — коммутативным моноидом.
- Любую полугруппу S можно превратить в моноид, просто присоединив элемент e, не входящий в S , и определив e • s = s = s • e для всех s ∈ S . Это преобразование любой полугруппы в моноид осуществляется свободным функтором между категорией полугрупп и категорией моноидов. [3]
- Таким образом, идемпотентный моноид (иногда известный как -first ) может быть сформирован путем присоединения единичного элемента e к левой нулевой полугруппе над множеством S. find Противоположный моноид (иногда называемый find-last формируется из полугруппы правых нулей над S. )
- Присоедините тождество e к полугруппе левых нулей с двумя элементами {lt, gt} . Затем полученный идемпотентный моноид {lt, e , gt} моделирует лексикографический порядок последовательности с учетом порядков ее элементов, где e представляет равенство.
- Таким образом, идемпотентный моноид (иногда известный как -first ) может быть сформирован путем присоединения единичного элемента e к левой нулевой полугруппе над множеством S. find Противоположный моноид (иногда называемый find-last формируется из полугруппы правых нулей над S. )
- Базовый набор любого кольца с операцией сложения или умножения. (По определению кольцо имеет мультипликативное тождество 1. )
- , Целые числа рациональные числа , действительные числа или комплексные числа со сложением или умножением в качестве операции. [4]
- Набор всех размера n на n матриц в заданном кольце со сложением или умножением матриц в качестве операции.
- Множество всех конечных строк в некотором фиксированном алфавите Σ образует моноид с конкатенации строк операцией служит . Пустая строка элементом идентификации. Этот моноид обозначается Σ ∗ и называется свободным моноидом над Σ . Оно не коммутативно, если Σ имеет хотя бы два элемента.
- Для любого моноида M моноид противоположный M на имеет тот же набор несущих и идентификационный элемент, что и M , и его работа определяется x • на y знак равно y • Икс . Любой коммутативный моноид является противоположным себе моноидом.
- Учитывая два множества M и N, наделенные структурой моноида (или, вообще говоря, любое конечное число моноидов, M 1 , ..., M k ), их декартово произведение M × N с бинарной операцией и единичным элементом, определенными на соответствующих координат, называемое прямым произведением , также является моноидом (соответственно M 1 × ⋅⋅⋅ × M k ). [5]
- Зафиксируйте моноид M . Множество всех функций из данного множества до M также является моноидом. Элемент идентификации — это постоянная функция, сопоставляющая любое значение с идентификатором M ; ассоциативная операция определяется поточечно .
- Зафиксируйте моноид M с операцией • и единичным элементом и рассмотрим его степенное множество P ( M ), из всех подмножеств M. e состоящее Бинарная операция для таких подмножеств может быть определена как S • T = { s • t : s ∈ S , t ∈ T } . Это превращает P ( M ) в моноид с единичным элементом { e } . Точно так же степенное множество группы G является моноидом относительно произведения групповых подмножеств .
- Пусть S — множество. Множество всех функций S → S образует моноид при композиции функций . Идентичность — это просто функция тождества . также называют полным моноидом преобразования S Его . Если S конечна с n элементами, моноид функций на S конечен с n н элементы.
- Обобщая предыдущий пример, пусть C — категория , а X объект C. — Множество всех эндоморфизмов X End , обозначенное композиции C ( X ) , образует моноид относительно морфизмов . Дополнительную информацию о взаимосвязи между теорией категорий и моноидами см. ниже.
- Множество гомеоморфизма классов компактных поверхностей со связной суммой . Ее единичным элементом является класс обычной 2-сферы. Кроме того, если a обозначает класс тора , а b обозначает класс проективной плоскости, то каждый элемент c моноида имеет уникальное выражение вида c = na + mb, где n — положительное целое число и m = 0, 1 или 2 . У нас есть 3 b = a + b .
- Пусть ⟨ f ⟩ — циклический моноид порядка n , то есть ⟨ f ⟩ = { f 0 , ж 1 , ..., ж п -1 } . Тогда f н = е к для некоторого 0 ≤ k < n . Фактически, каждый такой k дает отдельный моноид порядка n , и каждый циклический моноид изоморфен одному из них.
Более того, f можно рассматривать как функцию в точках {0, 1, 2, ..., n −1}, заданную формулой
Умножение элементов в ⟨ f ⟩ затем задаётся композицией функций.
Когда k = 0 , функция f является перестановкой {0, 1, 2, ..., n −1} и дает уникальную циклическую группу порядка n .
Свойства [ править ]
Аксиомы моноида подразумевают, что единичный элемент e уникален: если e и f являются единичными элементами моноида, то e = ef = f .
Продукты и возможности [ править ]
Для каждого неотрицательного целого числа n можно определить произведение любой последовательности ( a 1 , ..., a n ) из n элементов моноида рекурсивно: пусть 0 = e и пусть pm p = p m −1 • a m для 1 ≤ m ≤ n .
В качестве частного случая можно определить неотрицательные целые степени элемента x моноида: x 0 = 1 и х н = х п -1 • x для n ≥ 1 . Тогда х м + н = х м • х н для всех м , п ≥ 0 .
Обратимые элементы [ править ]
Элемент x называется обратимым , если существует элемент y такой, что x • y = e и y • x = e . Элемент y называется обратным элементу x . Инверсии, если они существуют, уникальны: если y и z являются инверсиями x , то по ассоциативности y = ey = ( zx ) y = z ( xy ) = ze = z . [6]
Если x обратим, скажем, с обратным y , то можно определить отрицательные степени x, установив x − п = и н для каждого n ≥ 1 ; это делает уравнение x м + н = х м • х н для всех m , n ∈ Z. справедливы
Совокупность всех обратимых элементов моноида вместе с операцией • образует группу .
Группа Гротендика [ править ]
Не каждый моноид находится внутри группы. Например, вполне возможно иметь моноид, в котором существуют два элемента a и b, такие что a • b = a выполняется, даже если b не является единичным элементом. Такой моноид не может быть вложен в группу, потому что в группе, умножив обе части на обратную величину a, получим b = e , что неверно.
Моноид ( M , •) обладает свойством сокращения (или является сокращающимся), если для всех a , b и c в M равенство a • b = a • c влечет b = c , а равенство b • a = c • а подразумевает б = с .
Коммутативный моноид со свойством сокращения всегда можно вложить в группу с помощью групповой конструкции Гротендика . Именно так аддитивная группа целых чисел (группа с операцией + ) строится из аддитивного моноида натуральных чисел (коммутативного моноида с операцией + и свойством отмены). Однако некоммутативный сокращающийся моноид не обязательно должен быть вложимым в группу.
Если моноид обладает свойством сокращения и конечен , то он фактически является группой. [с]
Право- и левосократяющиеся элементы моноида поочередно образуют субмоноид (т. е. замкнуты относительно операции и, очевидно, содержат единицу). Это означает, что сокращающиеся элементы любого коммутативного моноида можно расширить до группы.
Свойство сокращения в моноиде не обязательно для выполнения конструкции Гротендика - достаточно коммутативности. Однако если коммутативный моноид не обладает свойством сокращения, гомоморфизм моноида в его группу Гротендика не является инъективным. Точнее, если a • b = a • c , то b и c имеют один и тот же образ в группе Гротендика, даже если b ≠ c . В частности, если моноид имеет поглощающий элемент , то его группа Гротендика является тривиальной группой .
Виды моноидов [ править ]
Обратный моноид — это моноид, в котором для каждого a в M существует единственный a −1 в M такой, что a = a • a −1 • а и а −1 = а −1 • а • а −1 . Если инверсный моноид сократим, то он является группой.
В противоположном направлении моноид без нулевой суммы — это моноид, записанный аддитивно, в котором из a + b = 0 следует, что a = 0 и b = 0 : [7] эквивалентно, что ни один элемент, кроме нуля, не имеет аддитивного обратного.
операторов моноиды и Действия
Пусть M — моноид с бинарной операцией, обозначенной •, и единичным элементом, обозначенным e . Тогда (левый) M -действие (или левый действие над M ) представляет собой множество X вместе с операцией ⋅: M × X → X , которая совместима со структурой моноида следующим образом:
- для всех x в X : е ⋅ x знак равно x ;
- для всех a , b в M и x в X : а ⋅ ( б ⋅ Икс ) знак равно ( а • б ) ⋅ Икс .
Это аналог действия (левой) группы в теории моноида . Правые М -акты определяются аналогично. Моноид с действием также известен как моноид оператора . примерами являются переходные системы полуавтоматов Важными . Полугруппу преобразований можно превратить в моноид оператора путем присоединения тождественного преобразования.
гомоморфизмы Моноидные
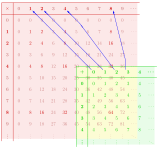
Гомоморфизмом и между двумя моноидами ( M , ∗) ( N , •) называется функция f : M → N такая, что
- ж ( Икс * y ) знак равно ж ( Икс ) • ж ( y ) для всех x , y в M
- ж ( е M ) знак равно е N ,
где e M и e N — тождества на M и N соответственно. Моноидные гомоморфизмы иногда называют просто моноидными морфизмами .
Не каждый гомоморфизм полугруппы между моноидами является моноидным гомоморфизмом, поскольку он не может отображать тождество в тождество целевого моноида, даже если тождество является тождеством образа гомоморфизма. [д] Например, рассмотрим [ Z ] n , набор классов вычетов по модулю n, оснащенный функцией умножения. В частности, [1] n является единичным элементом. Функция f : [ Z ] 3 → [ Z ] 6, заданная формулой [ k ] 3 ↦ [3 k ] 6, является гомоморфизмом полугруппы, поскольку [3 k ⋅ 3 l ] 6 = [9 kl ] 6 = [3 kl ] 6 . Однако f ([1] 3 ) = [3] 6 ≠ [1] 6 , поэтому гомоморфизм моноида — это гомоморфизм полугруппы между моноидами, который отображает идентичность первого моноида в идентичность второго моноида, и последнее условие не может быть опущено.
Напротив, гомоморфизм полугрупп между группами всегда является гомоморфизмом группы , поскольку он обязательно сохраняет идентичность (потому что в целевой группе гомоморфизма единичный элемент является единственным элементом x таким, что x ⋅ x = x ).
Биективный моноидным моноидный гомоморфизм называется изоморфизмом . Два моноида называются изоморфными, если между ними существует моноидный изоморфизм.
Эквациональное представление [ править ]
Моноидам может быть предоставлено представление , во многом таким же образом, как группы могут быть определены посредством представления группы . Это можно сделать, задав набор генераторов Σ и набор отношений на свободном моноиде Σ. ∗ . Это можно сделать путем расширения (конечных) бинарных отношений на Σ ∗ к моноидным сравнениям, а затем построим фактормоноид, как указано выше.
Для бинарного отношения R ⊂ Σ ∗ × С ∗ , его симметричное замыкание определяется как R ∪ R −1 . Это можно расширить до симметричного отношения E ⊂ Σ ∗ × С ∗ определив x ~ E y тогда и только тогда, когда x = sut и y = svt для некоторых строк u , v , s , t ∈ Σ ∗ с ( ты , v ) ∈ р ∪ р −1 . Наконец, берется рефлексивное и транзитивное замыкание E , которое тогда является моноидным сравнением.
В типичной ситуации отношение R просто задается в виде набора уравнений, так что R = { u 1 = v 1 , ... un , = v n } . Так, например,
— эквациональное представление бициклического моноида , а
— пластический моноид степени 2 (имеет бесконечный порядок). Элементы этого пластического моноида можно записать как для целых чисел i , j , k , поскольку соотношения показывают, что ba коммутирует как с a, так и с b .
с категорий Связь теорией
| Закрытие | Ассоциативный | Личность | Отмена | коммутативный | |
|---|---|---|---|---|---|
| Частичная магма | Ненужный | Ненужный | Ненужный | Ненужный | Ненужный |
| Полугруппоид | Ненужный | Необходимый | Ненужный | Ненужный | Ненужный |
| Малая категория | Ненужный | Необходимый | Необходимый | Ненужный | Ненужный |
| группоид | Ненужный | Необходимый | Необходимый | Необходимый | Ненужный |
| Коммутативный группоид | Ненужный | Необходимый | Необходимый | Необходимый | Необходимый |
| Магма | Необходимый | Ненужный | Ненужный | Ненужный | Ненужный |
| Коммутативная магма | Необходимый | Ненужный | Ненужный | Ненужный | Необходимый |
| Квазигруппа | Необходимый | Ненужный | Ненужный | Необходимый | Ненужный |
| Коммутативная квазигруппа | Необходимый | Ненужный | Ненужный | Необходимый | Необходимый |
| Ассоциативная квазигруппа | Необходимый | Необходимый | Ненужный | Необходимый | Ненужный |
| Коммутативно-ассоциативная квазигруппа | Необходимый | Необходимый | Ненужный | Необходимый | Необходимый |
| Единая магма | Необходимый | Ненужный | Необходимый | Ненужный | Ненужный |
| Коммутативная унитарная магма | Необходимый | Ненужный | Необходимый | Ненужный | Необходимый |
| Петля | Необходимый | Ненужный | Необходимый | Необходимый | Ненужный |
| Коммутативный цикл | Необходимый | Ненужный | Необходимый | Необходимый | Необходимый |
| Полугруппа | Необходимый | Необходимый | Ненужный | Ненужный | Ненужный |
| Коммутативная полугруппа | Необходимый | Необходимый | Ненужный | Ненужный | Необходимый |
| Моноид | Необходимый | Необходимый | Необходимый | Ненужный | Ненужный |
| Коммутативный моноид | Необходимый | Необходимый | Необходимый | Ненужный | Необходимый |
| Группа | Необходимый | Необходимый | Необходимый | Необходимый | Ненужный |
| Абелева группа | Необходимый | Необходимый | Необходимый | Необходимый | Необходимый |
Моноиды можно рассматривать как особый класс категорий . Действительно, аксиомы, необходимые для моноидной операции, в точности совпадают с аксиомами, необходимыми для композиции морфизмов , если они ограничены набором всех морфизмов, источником и целью которых является данный объект. [8] То есть,
- Моноид — это, по сути, то же самое, что и категория с единственным объектом.
Точнее, по моноиду ( M , •) элементами M. можно построить небольшую категорию только с одним объектом, морфизмы которой являются Композиция морфизмов задается моноидной операцией • .
Аналогично, моноидные гомоморфизмы — это просто функторы между отдельными категориями объектов. [8] Таким образом, эта конструкция дает эквивалентность между категорией (малых) моноидов Mon и полной подкатегорией категории (малых) категорий Cat . Аналогично категория групп эквивалентна другой полной подкатегории Cat .
В этом смысле теорию категорий можно рассматривать как расширение концепции моноида. Многие определения и теоремы о моноидах можно обобщить на небольшие категории с более чем одним объектом. Например, фактор категории с одним объектом — это просто фактормоноид.
Моноиды, как и другие алгебраические структуры, также образуют свою собственную категорию Mon , объекты которой являются моноидами, а морфизмы — гомоморфизмами моноидов. [8]
Существует также понятие моноидного объекта , которое представляет собой абстрактное определение того, что такое моноид в категории. Моноидный объект в Set — это просто моноид.
Моноиды в информатике [ править ]
В информатике многие абстрактные типы данных могут быть наделены моноидной структурой. В обычном шаблоне последовательность элементов моноида « складывается » или «накапливается» для получения окончательного значения. Например, многим итеративным алгоритмам необходимо обновлять некий «промежуточный итог» на каждой итерации; этот шаблон может быть элегантно выражен с помощью моноидной операции. Альтернативно, ассоциативность моноидных операций гарантирует, что операцию можно распараллелить , используя сумму префиксов или аналогичный алгоритм, чтобы эффективно использовать несколько ядер или процессоров.
Учитывая последовательность значений типа M с единичным элементом ε и ассоциативной операцией • , операция складки определяется следующим образом:
Кроме того, любую структуру данных можно «свернуть» аналогичным образом, учитывая сериализацию ее элементов. Например, результат «свертывания» двоичного дерева до и после порядка может отличаться в зависимости от обхода дерева .
MapReduce [ править ]
Применением моноидов в информатике является так называемая MapReduce модель программирования (см. Кодирование Map-Reduce как моноида со сворачиванием влево ). MapReduce в вычислительной технике состоит из двух или трех операций. Учитывая набор данных, «Карта» состоит из сопоставления произвольных данных с элементами определенного моноида. «Уменьшение» заключается в складывании этих элементов так, чтобы в итоге мы получили только один элемент.
Например, если у нас есть мультимножество , в программе оно представляется в виде отображения элементов на их номера. В этом случае элементы называются ключами. Количество различных ключей может быть слишком большим, и в этом случае мультимножество шардируется . Чтобы правильно завершить сокращение, на этапе «Перетасовка» данные перегруппируются по узлам. Если нам не нужен этот шаг, вся операция Map/Reduce состоит из сопоставления и сокращения; обе операции распараллеливаемы: первая из-за ее поэлементной природы, вторая - из-за ассоциативности моноида.
Полные моноиды [ править ]
Полный моноид — это коммутативный моноид, снабженный операцией бесконечной суммы. для любого набора индексов I такого, что [9] [10] [11] [12]
и
- .
Упорядоченный моноид — это коммутативный моноид M вместе с частичным упорядочением ≤ такой, что a ≥ 0 для каждого a ∈ M , а a ≤ b влечет за собой a + c ≤ b + c для всех a , b , c ∈ M. коммутативный
Непрерывный моноид — это упорядоченный коммутативный моноид ( M , ≤), в котором каждое направленное подмножество имеет наименьшую верхнюю границу , и эти наименьшие верхние границы совместимы с операцией моноида:
для каждого a ∈ M и направленного подмножества S из M .
Если ( M , ≤) — непрерывный моноид, то для любого набора индексов I и набора элементов ( a i ) i ∈ I можно определить
и M вместе с этой операцией бесконечной суммы представляет собой полный моноид. [12]
См. также [ править ]
- Декартовский моноид
- Отношения Грина
- Монада (функциональное программирование)
- Полукольцо и алгебра Клини
- Проблема с высотой звезды
- Ведическая площадь
- Фробениоид
Примечания [ править ]
- ^ Если и , и e2 удовлетворяют выше уравнениям e1 то = e1 приведенным • e2 e2 = e1 , .
- ^ Некоторые авторы опускают требование о том, что субмоноид должен содержать единичный элемент из своего определения, требуя только того, чтобы он имел единичный элемент, который может отличаться от элемента M .
- ^ Доказательство: зафиксируйте элемент x в моноиде. Поскольку моноид конечен, x н = х м для некоторого m > n > 0 . Но тогда, отменяя, мы получаем, что x м - п = e , где e — тождество. Следовательно, x • x м - п -1 = e , поэтому x имеет обратный.
- ^ f ( x ) * f ( e M ) знак равно f ( x * e M ) знак равно f ( x ) для каждого x в M , когда f - гомоморфизм полугруппы и e M - тождество ее моноида области M .
Цитаты [ править ]
- ^ Джейкобсон 2009
- ^ Гондран и Мину 2008 , с. 13
- ^ Родос и Стейнберг 2009 , с. 22
- ^ Джейкобсон 2009 , с. 29, примеры 1, 2, 4 и 5
- ^ Джейкобсон 2009 , с. 35
- ^ Джейкобсон 2009 , с. 31, §1.2
- ^ Защита 1996 г.
- ^ Jump up to: Перейти обратно: а б с Аводи 2006 , с. 10
- ^ Дросте и Куич 2009 , стр. 7–10.
- ^ Хебиш 1992
- ^ Куич 1990
- ^ Jump up to: Перейти обратно: а б Куич 2011 .
Ссылки [ править ]
- Аводи, Стив (2006). Теория категорий . Оксфордские руководства по логике. Том. 49. Издательство Оксфордского университета . ISBN 0-19-856861-4 . Збл 1100.18001 .
- Дросте, М.; Куич, В. (2009), «Полукольца и формальные степенные ряды», Справочник по взвешенным автоматам , стр. 3–28, CiteSeerX 10.1.1.304.6152 , doi : 10.1007/978-3-642-01492-5_1
- Гондран, Мишель; Мину, Мишель (2008). Графы, диоиды и полукольца: новые модели и алгоритмы . Серия интерфейсов исследования операций/информатики. Том. 41. Дордрехт: Springer-Verlag . ISBN 978-0-387-75450-5 . Збл 1201.16038 .
- Хебиш, Удо (1992). «Алгебраическая теория бесконечных сумм с приложениями к полугруппам и полукольцам». Байройтские математические сочинения (на немецком языке). 40 :21–152. Збл 0747.08005 .
- Хоуи, Джон М. (1995), Основы теории полугрупп , Монографии Лондонского математического общества. Новая серия, том. 12, Оксфорд: Clarendon Press, ISBN 0-19-851194-9 , Збл 0835.20077
- Джейкобсон, Натан (1951), Лекции по абстрактной алгебре , том. Я, Компания Д. Ван Ностранда, ISBN 0-387-90122-1
- Джейкобсон, Натан (2009), Основная алгебра , том. 1 (2-е изд.), Дувр, ISBN 978-0-486-47189-1
- Килп, Мати; Кнауэр, Ульрих; Михалев, Александр В. (2000), Моноиды, действия и категории. С приложениями для сплетения изделий и графиков. Справочник для студентов и исследователей , De Gruyter Expositions in Mathematics, vol. 29, Берлин: Вальтер де Грюйтер, ISBN 3-11-015248-7 , Збл 0945.20036
- Куич, Вернер (1990). «ω-непрерывные полукольца, алгебраические системы и автоматы с магазинным магазином» . В Патерсоне, Майкл С. (ред.). Автоматы, языки и программирование: 17-й международный коллоквиум, Уорикский университет, Англия, 16–20 июля 1990 г., Труды . Конспекты лекций по информатике. Том. 443. Шпрингер-Верлаг . стр. 103–110. ISBN 3-540-52826-1 .
- Куич, Вернер (2011). «Алгебраические системы и автоматы с понижением». В Куиче, Вернер (ред.). Алгебраические основы информатики. Очерки, посвященные Симеону Бозапалидису по случаю его выхода на пенсию . Конспекты лекций по информатике. Том. 7020. Берлин: Springer-Verlag . стр. 228–256. ISBN 978-3-642-24896-2 . Збл 1251.68135 .
- Лотер, М. , изд. (1997), Комбинаторика слов , Энциклопедия математики и ее приложений, том. 17 (2-е изд.), Cambridge University Press , номер документа : 10.1017/CBO9780511566097 , ISBN. 0-521-59924-5 , МР 1475463 , Збл 0874.20040
- Роудс, Джон; Стейнберг, Бенджамин (2009), q-теория конечных полугрупп: новый подход , Монографии Springer по математике, том. 71, Спрингер, ISBN 9780387097817
- Верунг, Фридрих (1996). «Тензорные произведения структур с интерполяцией» . Тихоокеанский математический журнал . 176 (1): 267–285. дои : 10.2140/pjm.1996.176.267 . S2CID 56410568 . Збл 0865.06010 .
Внешние ссылки [ править ]
- «Моноид» , Математическая энциклопедия , EMS Press , 2001 [1994]
- Вайсштейн, Эрик В. «Моноид» . Математический мир .
- Моноид в PlanetMath .











