Теория групп

В этой статье рассматриваются расширенные понятия. Основные темы см. в разделе Группа (математика) .

Чтобы узнать о теории групп в социальных науках, см. Социальную группу .

Популярная головоломка «Кубик Рубика» , изобретенная в 1974 году Эрно Рубиком , использовалась в качестве иллюстрации групп перестановок . См. группу «Кубик Рубика» .

В абстрактной алгебре теория групп изучает алгебраические структуры, известные как группы . Понятие группы является центральным в абстрактной алгебре: другие известные алгебраические структуры, такие как кольца , поля и векторные пространства , можно рассматривать как группы, наделенные дополнительными операциями и аксиомами . Группы повторяются во всей математике, и методы теории групп повлияли на многие разделы алгебры. Линейные алгебраические группы и группы Ли — это две ветви теории групп, которые получили развитие и стали самостоятельными предметными областями.

Различные физические системы, такие как кристаллы и атом водорода , а также три из четырех известных фундаментальных сил во Вселенной, можно моделировать с помощью групп симметрии . Таким образом, теория групп и тесно связанная с ней теория представлений имеют множество важных приложений в физике , химии и материаловедении . Теория групп также занимает центральное место в криптографии с открытым ключом .

Ранняя история теории групп датируется XIX веком. Одно из важнейших математических достижений XX века. Это совместная работа, занявшая более 10 000 журнальных страниц и в основном опубликованная в период с 1960 по 2004 год, завершилась полной классификацией конечных простых групп .

История

Основная статья: История теории групп

Теория групп имеет три основных исторических источника: теорию чисел , теорию алгебраических уравнений и геометрию . Направление теории чисел было начато Леонардом Эйлером и развито работами Гаусса по модульной арифметике , аддитивным и мультипликативным группам, связанным с квадратичными полями . Ранние результаты о группах перестановок были получены Лагранжем , Руффини и Абелем в их поисках общих решений полиномиальных уравнений высокой степени. Эварист Галуа ввёл термин «группа» и установил связь, теперь известную как теория Галуа , между зарождающейся теорией групп и теорией поля . В геометрии группы сначала приобрели важное значение в проективной геометрии , а затем и в неевклидовой геометрии . Феликса Кляйна в Программа Эрлангене провозгласила теорию групп организующим принципом геометрии.

Галуа в 1830-х годах был первым, кто использовал группы для определения разрешимости полиномиальных уравнений . Артур Кэли и Огюстен Луи Коши продвинули эти исследования дальше, создав теорию групп перестановок. Второй исторический источник групп проистекает из геометрических ситуаций. В попытке разобраться с возможными геометриями (такими как евклидова , гиперболическая или проективная геометрия ) с помощью теории групп Феликс Кляйн инициировал Эрлангенскую программу . Софус Ли в 1884 году начал использовать группы (теперь называемые группами Ли ), связанные с аналитическими задачами. В-третьих, группы сначала неявно, а затем явно использовались в алгебраической теории чисел .

Различный объем этих ранних источников привел к появлению разных представлений о группах. Теория групп была унифицирована примерно с 1880 года. С тех пор влияние теории групп постоянно росло, что привело к рождению абстрактной алгебры в начале 20-го века, теории представлений и многих других влиятельных побочных областей. Классификация конечных простых групп — это обширная работа середины 20 века, в которой классифицируются все конечные простые группы .

Основные классы групп

Основная статья: Группа (математика)

Диапазон рассматриваемых групп постепенно расширился от конечных групп перестановок и специальных примеров матричных групп которые могут быть заданы посредством представления генераторов до абстрактных групп , и отношений .

Группы перестановок

Первым классом групп, подвергшимся систематическому изучению, были группы перестановок . Для любого множества X и набора G биекций X в , себя (известных как перестановки замкнутых относительно композиций и инверсий, G является группой действующей на X. ) , Если X состоит из n элементов, а состоит из всех перестановок, G — симметрическая группа Sn _; G вообще говоря, любая группа перестановок G является подгруппой симметрической группы X . Ранняя конструкция Кэли представляла любую группу как группу перестановок, действующую на себя ( X = G ) посредством левого регулярного представления .

Во многих случаях структуру группы подстановок можно изучить, используя свойства ее действия на соответствующем множестве. Например, таким образом доказывается, что при n ≥ 5 знакопеременная группа An _{, т. е} проста . не допускает собственных нормальных подгрупп . Этот факт играет ключевую роль в невозможности решения общего алгебраического уравнения степени n ≥ 5 в радикалах .

Группы матриц

Следующий важный класс групп — матричные группы , или линейные группы . Здесь G — множество, состоящее из обратимых матриц данного порядка n над полем K , замкнутым относительно произведений и обратных. Такая группа действует на n -мерном векторном пространстве K ^н линейными преобразованиями . Это действие делает матричные группы концептуально похожими на группы перестановок, а геометрию действия можно с пользой использовать для установления свойств группы G .

Группы трансформации

Группы перестановок и группы матриц представляют собой частные случаи групп преобразований : группы, которые действуют в определенном пространстве X, сохраняя присущую ему структуру. В случае групп перестановок X представляет собой множество; для матричных групп X — векторное пространство . Понятие группы преобразований тесно связано с понятием группы симметрии : группы преобразований часто состоят из всех преобразований, сохраняющих определенную структуру.

Теория групп преобразований образует мост, соединяющий теорию групп с дифференциальной геометрией . Длинная линия исследований, начавшаяся с Ли и Клейна , рассматривает действия групп на многообразиях посредством гомеоморфизмов или диффеоморфизмов . Сами группы могут быть дискретными или непрерывными .

Абстрактные группы

Большинство групп, рассматриваемых на первом этапе развития теории групп, были «конкретными», реализовавшимися через числа, перестановки или матрицы. Лишь в конце девятнадцатого века начала распространяться идея абстрактной группы , где «абстрактность» означает, что природа элементов игнорируется таким образом, что две изоморфные группы рассматриваются как одна и та же группа. Типичный способ определения абстрактной группы — через представление генераторов и отношений .

$G=\langle S|R\rangle .$

Важным источником абстрактных групп является построение фактор- или факторгруппы H G / H. группы G по нормальной группы подгруппе классов Группы полей алгебраических чисел были одними из первых примеров фактор-групп, представляющих большой интерес в теории чисел . Если группа G является группой перестановок на множестве X , фактор-группа G / H больше не действует на X ; но идея абстрактной группы позволяет не беспокоиться об этом несоответствии.

Смена точки зрения с конкретных групп на абстрактные делает естественным рассмотрение свойств групп, независимых от конкретной реализации или, выражаясь современным языком, инвариантных относительно изоморфизма , а также классов групп с заданным таким свойством: конечные группы , периодические группы , простые группы , разрешимые группы и так далее. Вместо того, чтобы исследовать свойства отдельной группы, стремятся установить результаты, применимые к целому классу групп. Новая парадигма имела первостепенное значение для развития математики: она предвещала создание абстрактной алгебры в работах Гильберта , Эмиля Артина , Эмми Нётер и математиков их школы.

Группы с дополнительной структурой

Важная разработка понятия группы происходит, если G наделена дополнительной структурой, в частности, топологического пространства , дифференцируемого многообразия или алгебраического многообразия . Если групповые операции m (умножение) и i (инверсия),

$m:G\times G\to G,(g,h)\mapsto gh,\quad i:G\to G,g\mapsto g^{-1},$

совместимы с этой структурой, то есть являются непрерывными , гладкими или регулярными (в смысле алгебраической геометрии) отображениями, то G — топологическая группа , группа Ли или алгебраическая группа .

Наличие дополнительной структуры связывает эти типы групп с другими математическими дисциплинами и означает, что для их изучения доступно больше инструментов. Топологические группы образуют естественную область абстрактного гармонического анализа , тогда как группы Ли (часто реализуемые как группы преобразований) являются основой дифференциальной геометрии и теории унитарных представлений . Некоторые классификационные вопросы, которые не могут быть решены в целом, могут быть решены для особых подклассов групп. Таким образом, компактные связные группы Ли полностью классифицированы. Существует плодотворная связь между бесконечными абстрактными группами и топологическими группами: всякий раз, когда группа Γ может быть реализована как решетка в топологической группе G , геометрия и анализ, относящиеся к G, дают важные результаты о Γ . Сравнительно недавнее направление в теории конечных групп использует их связи с компактными топологическими группами ( проконечными группами ): например, одна p -адическая аналитическая группа G имеет семейство частных, которые конечны. p -группы различных порядков, а свойства группы G переходят в свойства ее конечных факторов.

Разделы теории групп

Теория конечных групп

Основная статья: Конечная группа

В течение двадцатого века математики глубоко исследовали некоторые аспекты теории конечных групп, особенно локальную теорию конечных групп и теорию разрешимых и нильпотентных групп . Как следствие, была достигнута полная классификация конечных простых групп , а это означает, что теперь известны все те простые группы , из которых можно построить все конечные группы.

Во второй половине двадцатого века такие математики, как Шевалле и Стейнберг, также расширили наше понимание конечных аналогов классических групп и других родственных групп. Одним из таких семейств групп является семейство общих линейных групп над конечными полями . Конечные группы часто встречаются при рассмотрении симметрии математических илифизические объекты, когда эти объекты допускают лишь конечное число преобразований, сохраняющих структуру. Теория групп Ли ,которую можно рассматривать как имеющую дело с « непрерывной симметрией », находится под сильным влиянием связанных с ней групп Вейля . Это конечные группы, порожденные отражениями, действующими в конечномерном евклидовом пространстве . Таким образом, свойства конечных групп могут играть роль в таких предметах, как теоретическая физика и химия .

Представление групп

Основная статья: Теория представлений

Утверждение, что группа G действует на множестве X, означает, что каждый элемент G определяет биективное отображение на множестве X способом, совместимым со структурой группы. Когда X имеет больше структуры, полезно дополнительно ограничить это понятие: представление G в векторном пространстве V является гомоморфизмом группы :

$\rho :G\to \operatorname {GL} (V),$

где GL ( V обратимых линейных преобразований V. ) состоит из Другими словами, каждому элементу группы g сопоставлен автоморфизм ρ ( g ) такой, что ( g ) ∘ ρ ( h ) = ρ ( gh ) для любого h в G. ρ

Это определение можно понимать в двух направлениях, оба из которых порождают совершенно новые области математики. С одной стороны, это может дать новую информацию о группе G : часто групповая операция в G задается абстрактно, но через ρ она соответствует умножению матриц , что очень явно. С другой стороны, если хорошо понятная группа действует на сложный объект, это упрощает исследование рассматриваемого объекта. Например, если G конечна, известно, что V выше разлагается на неприводимые части (см. теорему Машке ). Этими частями, в свою очередь, гораздо легче управлять, чем целым V (по лемме Шура ).

Учитывая группу G , теория представлений спрашивает, какие представления G существуют. Существует несколько настроек, а используемые методы и полученные результаты в каждом случае весьма различны: теория представлений конечных групп и представления групп Ли являются двумя основными подобластями теории. группы Совокупность представлений определяется характерами . Например, полиномы Фурье можно интерпретировать как символы U(1) — группы комплексных чисел с абсолютным значением 1 , действующих на L ² -пространство периодических функций.

Теория лжи

Основная статья: Теория лжи

Группа Ли — это группа , которая также является дифференцируемым многообразием , обладающим тем свойством, что групповые операции совместимы с гладкой структурой . Группы Ли названы в честь Софуса Ли , заложившего основы теории групп непрерывных преобразований . Термин groupes de Lie впервые появился на французском языке в 1893 году в диссертации ученика Ли Артура Трессе , стр. 3.

Группы Ли представляют собой наиболее развитую теорию непрерывной симметрии математических объектов и структур , что делает их незаменимыми инструментами для многих разделов современной математики, а также для современной теоретической физики . Они обеспечивают естественную основу для анализа непрерывных симметрий дифференциальных уравнений ( дифференциальная теория Галуа ), во многом так же, как группы перестановок используются в теории Галуа для анализа дискретных симметрий алгебраических уравнений . Распространение теории Галуа на случай непрерывных групп симметрии было одной из основных мотиваций Ли.

Комбинаторная и геометрическая теория групп

Основная статья: Геометрическая теория групп

Группы можно описывать по-разному. Конечные группы можно описать, записав таблицу групп , состоящую из всех возможных умножений g • h . Более компактный способ определения группы — с помощью генераторов и отношений , также называемых представлением группы. Учитывая любой набор F генераторов $\{g_{i}\}_{i\in I}$, свободная группа , порожденная F, на группу G. сюръектируется Ядро этого отображения называется подгруппой отношений, порожденной некоторым D. подмножеством Презентация обычно обозначается $\langle F\mid D\rangle .$ Например, групповая презентация. $\langle a,b\mid aba^{-1}b^{-1}\rangle$ описывает группу, которая изоморфна $\mathbb {Z} \times \mathbb {Z} .$ Строка, состоящая из образующих символов и обратных им, называется словом .

Комбинаторная теория групп изучает группы с точки зрения генераторов и отношений. Это особенно полезно там, где выполняются предположения конечности, например, конечно порожденные группы или конечно представленные группы (т. е., кроме того, отношения конечны). Область использует связь графов через их фундаментальные группы . Фундаментальная теорема в этой области состоит в том, что каждая подгруппа свободной группы свободна.

Есть несколько естественных вопросов, возникающих при предоставлении группы путем ее презентации. Проблема со словами спрашивает, являются ли два слова фактически одним и тем же групповым элементом. Связав задачу с машинами Тьюринга , можно показать, что вообще не существует алгоритма, решающего эту задачу. Другая, как правило, более сложная и алгоритмически неразрешимая проблема — это проблема изоморфизма групп , которая спрашивает, действительно ли две группы, заданные разными представлениями, изоморфны. Например, группа с презентацией $\langle x,y\mid xyxyx=e\rangle ,$ изоморфна аддитивной группе целых чисел Z , хотя это может быть не сразу очевидно. (Письмо $z=xy$, у одного есть $G\cong \langle z,y\mid z^{3}=y\rangle \cong \langle z\rangle .$)

Граф Кэли ⟨ x, y ∣ ⟩, свободной группы ранга 2

Геометрическая теория групп решает эти проблемы с геометрической точки зрения, либо рассматривая группы как геометрические объекты, либо находя подходящие геометрические объекты, на которые группа действует. Первая идея уточняется с помощью графа Кэли , вершины которого соответствуют элементам группы, а ребра соответствуют правому умножению в группе. По двум элементам строится словесная метрика, определяемая длиной минимального пути между элементами. Теорема Милнора что если группа G действует разумным образом на метрическом пространстве X , например, на компактном многообразии , то G квазиизометрична и Сварца затем гласит , выглядит подобной на расстоянии) пространству X. (т. е .

Соединение групп и симметрия

Основная статья: Группа симметрии

структурированного объекта X Для любого симметрия — это отображение объекта на самого себя, сохраняющее структуру. Это происходит во многих случаях, например

• Если X — набор без дополнительной структуры, симметрия — это биективное отображение набора в себя, приводящее к появлению групп перестановок.
• Если объект X представляет собой набор точек на плоскости со своей метрической структурой или в любом другом метрическом пространстве , симметрия — это биекция набора самому себе, которая сохраняет расстояние между каждой парой точек (изометрия ) . называется группой изометрий X Соответствующая группа .
• Если вместо этого углы сохраняются , говорят о конформных отображениях . конформные отображения приводят к появлению клейнианских групп . Например,
• Симметрии не ограничиваются геометрическими объектами, но включают также алгебраические объекты. Например, уравнение $x^{2}-3=0$ имеет два решения ${\sqrt {3}}$ и $-{\sqrt {3}}$. В этом случае группа, которая меняет местами два корня, является группой Галуа, принадлежащей уравнению. Каждое полиномиальное уравнение с одной переменной имеет группу Галуа, то есть определенную группу перестановок на его корнях.

Аксиомы группы формализуют существенные аспекты симметрии . Симметрии образуют группу: они замкнуты , потому что если взять симметрию объекта, а затем применить другую симметрию, результатом все равно будет симметрия. Тождество, сохраняющее объект фиксированным, всегда является симметрией объекта. Существование обратных гарантируется отменой симметрии, а ассоциативность возникает из-за того, что симметрии являются функциями в пространстве, а композиция функций ассоциативна.

Теорема Фрухта гласит, что каждая группа является группой симметрии некоторого графа . Таким образом, каждая абстрактная группа на самом деле является симметрией некоторого явного объекта.

Поговорку о «сохранении структуры» объекта можно уточнить, работая с категорией . Карты, сохраняющие структуру, тогда являются морфизмами , а группа симметрии — группой автоморфизмов рассматриваемого объекта.

теории

Применений теории групп имеется множество. Почти все структуры абстрактной алгебры являются частными случаями групп. Кольца , например, можно рассматривать как абелевы группы (соответствующие сложению) вместе со второй операцией (соответствующей умножению). Таким образом, аргументы теории групп лежат в основе значительной части теории этих сущностей.

Теория Галуа

Основная статья: теория Галуа

Теория Галуа использует группы для описания симметрии корней многочлена (точнее, автоморфизмов алгебр, порожденных этими корнями). Фундаментальная теорема теории Галуа обеспечивает связь между алгебраическими расширениями полей и теорией групп. Он дает эффективный критерий разрешимости полиномиальных уравнений в терминах разрешимости соответствующей группы Галуа . Например, S ₅ , симметрическая группа из 5 элементов, неразрешима, а это означает, что общее уравнение пятой степени не может быть решено с помощью радикалов, как это могут быть уравнения более низкой степени. Эта теория, являющаяся одним из исторических корней теории групп, до сих пор плодотворно применяется для получения новых результатов в таких областях, как теория полей классов .

Алгебраическая топология

Основная статья: Алгебраическая топология

Алгебраическая топология - это еще одна область, которая явно связывает группы с объектами, интересующими теорию. Там группы используются для описания определенных инвариантов топологических пространств . Их называют «инвариантами», потому что они определены таким образом, что не изменяются, если пространство подвергается некоторой деформации . Например, фундаментальная группа «подсчитывает», сколько путей в пространстве существенно различаются. Гипотеза Пуанкаре , доказанная в 2002/2003 году Григорием Перельманом , является ярким применением этой идеи. Однако влияние не является однонаправленным. Например, алгебраическая топология использует пространства Эйленберга – Маклейна , которые представляют собой пространства с предписанными гомотопическими группами . Аналогичным образом алгебраическая K-теория в некотором смысле опирается на классификацию пространств групп. Наконец, название периодической подгруппы бесконечной группы показывает наследие топологии в теории групп.

Тор. Его абелева групповая структура индуцирована отображением C → C /( Z + τ Z ) , где τ — параметр, находящийся в верхней полуплоскости .

Алгебраическая геометрия

Основная статья: Алгебраическая геометрия

Алгебраическая геометрия также во многих отношениях использует теорию групп. Абелевы многообразия были введены выше. Наличие групповой операции дает дополнительную информацию, которая делает эти разновидности особенно доступными. Они также часто служат проверкой новых гипотез. (Например, гипотеза Ходжа одномерный случай, а именно эллиптические кривые (в некоторых случаях).) Особенно подробно изучен . Они интересны как теоретически, так и практически. С другой стороны, торические многообразия — это алгебраические многообразия, на которые действует тор . Тороидальные вложения недавно привели к прогрессу в алгебраической геометрии , в частности к разрешению особенностей .

теория

Основная статья: Алгебраическая теория чисел

Алгебраическая теория чисел использует группы для некоторых важных приложений. Например, формула произведения Эйлера :

${\begin{aligned}\sum _{n\geq 1}{\frac {1}{n^{s}}}&=\prod _{p{\text{ prime}}}{\frac {1}{1-p^{-s}}},\\\end{aligned}}\!$

отражает тот факт , что любое целое число уникальным образом разлагается на простые числа . Неверность этого утверждения для более общих колец приводит к появлению групп классов и регулярных простых чисел , которые фигурируют в Куммером трактовке Великой теоремы Ферма .

Гармонический анализ

Основная статья: Гармонический анализ

Анализ групп Ли и некоторых других групп называется гармоническим анализом . Меры Хаара , то есть интегралы, инвариантные относительно перевода в группу Ли, используются для распознавания образов и других методов обработки изображений .

Комбинаторика

В комбинаторике понятие группы перестановок и понятие группового действия часто используются для упрощения подсчета множества объектов; см., в частности, лемму Бернсайда .

Квинтовый круг может иметь циклическую групповую структуру.

Музыка

Наличие 12- периодичности в квинтовом круге дает применение элементарной теории групп в теории музыкальных множеств . Трансформационная теория моделирует музыкальные трансформации как элементы математической группы.

Физика

В физике группы важны, потому что они описывают симметрии, которым, по-видимому, подчиняются законы физики. Согласно теореме Нётер , каждой непрерывной симметрии физической системы соответствует закон сохранения системы. Физики очень интересуются представлениями групп, особенно групп Ли, поскольку эти представления часто указывают путь к «возможным» физическим теориям. Примеры использования групп в физике включают Стандартную модель , калибровочную теорию , группу Лоренца и группу Пуанкаре .

Теорию групп можно использовать для устранения неполноты статистических интерпретаций механики, разработанных Уиллардом Гиббсом , касающихся суммирования бесконечного числа вероятностей для получения значимого решения.

Химия и материаловедение

Основная статья: Молекулярная симметрия

В химии и материаловедении используются точечные группы для классификации правильных многогранников, а также симметрии молекул и пространственные группы для классификации кристаллических структур . Назначенные группы затем можно использовать для определения физических свойств (таких как химическая полярность и хиральность ), спектроскопических свойств (особенно полезно для рамановской спектроскопии , инфракрасной спектроскопии , спектроскопии кругового дихроизма, спектроскопии магнитного кругового дихроизма, спектроскопии УФ/видимого света и спектроскопии флуоресценции). и построить молекулярные орбитали .

Молекулярная симметрия отвечает за многие физические и спектроскопические свойства соединений и предоставляет важную информацию о том, как протекают химические реакции. Чтобы назначить точечную группу для любой данной молекулы, необходимо найти набор присутствующих на ней операций симметрии. Операция симметрии — это такое действие, как вращение вокруг оси или отражение через плоскость зеркала. Другими словами, это операция, которая перемещает молекулу так, что она становится неотличима от исходной конфигурации. В теории групп оси вращения и зеркальные плоскости называются «элементами симметрии». Этими элементами могут быть точка, линия или плоскость, относительно которой осуществляется операция симметрии. Операции симметрии молекулы определяют конкретную точечную группу этой молекулы.

Молекула воды с осью симметрии

В химии существует пять важных операций симметрии. Это операция тождества ( E) , операция вращения или правильного вращения ( ) _, операция отражения ( σ ), инверсия ( i ) и операция отражения вращения или неправильный поворот ( Sn _Cn ). Операция тождества ( E ) заключается в том, чтобы оставить молекулу такой, какая она есть. Это эквивалентно любому количеству полных оборотов вокруг любой оси. Это симметрия всех молекул, тогда как группа симметрии хиральной молекулы состоит только из операции тождества. Операция тождества является характеристикой каждой молекулы, даже если она не обладает симметрией. Вращение вокруг оси ( C _n ) заключается во вращении молекулы вокруг определенной оси на определенный угол. Это вращение на угол 360°/ n , где n — целое число, вокруг оси вращения. Например, если молекула воды повернётся на 180° вокруг оси, проходящей через атом кислорода и между атомами водорода , она окажется в той же конфигурации, в которой была изначально. В данном случае n = 2 , поскольку его двукратное применение дает операцию идентичности. В молекулах с более чем одной осью вращения C _{Ось n} , имеющая наибольшее значение n, является осью вращения высшего порядка или главной осью. Например, в трифториде бора (BF ₃ ) ось вращения высшего порядка — C ₃ , поэтому главная ось вращения — C ₃ .

В процессе отражения ( σ ) многие молекулы имеют зеркальные плоскости, хотя они могут быть неочевидными. Операция отражения меняется местами влево и вправо, как если бы каждая точка переместилась перпендикулярно плоскости в положение точно на такое же расстояние от плоскости, как и в начале. Когда плоскость перпендикулярна главной оси вращения, ее называют σ _h (горизонтальной). Другие плоскости, содержащие главную ось вращения, обозначаются как вертикальные ( σ _v ) или двугранные ( σ _d ).

Инверсия (i) — более сложная операция. Каждая точка перемещается через центр молекулы в положение, противоположное исходному положению и на такое же расстояние от центральной точки, с которого она началась. Многие молекулы, которые на первый взгляд кажутся имеющими центр инверсии, не имеют его; например, метан и другие тетраэдрические молекулы лишены инверсионной симметрии. Чтобы убедиться в этом, возьмите модель метана с двумя атомами водорода в вертикальной плоскости справа и двумя атомами водорода в горизонтальной плоскости слева. Инверсия приводит к появлению двух атомов водорода в горизонтальной плоскости справа и двух атомов водорода в вертикальной плоскости слева. Таким образом, инверсия не является операцией симметрии метана, поскольку ориентация молекулы после операции инверсии отличается от исходной ориентации. И последняя операция — неправильный поворот или операция отражения вращения ( Sn ₎ требует поворота на 360°/ n с последующим отражением через плоскость, перпендикулярную оси вращения.

Криптография

Циклическая группа Z ₂₆ лежит в основе шифра Цезаря .

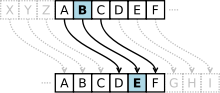
Очень большие группы простого порядка, построенные в криптографии на эллиптических кривых, служат для криптографии с открытым ключом . Криптографические методы такого типа выигрывают от гибкости геометрических объектов и, следовательно, от их групповой структуры, а также от сложной структуры этих групп, что дискретного логарифма очень затрудняет вычисление . Один из самых ранних протоколов шифрования, шифр Цезаря , также можно интерпретировать как (очень простую) групповую операцию. Большинство криптографических схем тем или иным образом используют группы. В частности, при обмене ключами Диффи-Хеллмана используются конечные циклические группы . Таким образом, термин «криптография на основе групп» относится главным образом к криптографическим протоколам , которые используют бесконечные неабелевы группы, такие как группа кос .

См. также

• Список тем теории групп
• Примеры групп

Ссылки

• Борель, Арманд (1991), Линейные алгебраические группы , Тексты для аспирантов по математике, том. 126 (2-е изд.), Берлин, Нью-Йорк: Springer-Verlag , doi : 10.1007/978-1-4612-0941-6 , ISBN  978-0-387-97370-8 , МР   1102012
• Картер, Натан К. (2009), Теория визуальных групп , Серия учебных материалов, Математическая ассоциация Америки , ISBN  978-0-88385-757-1 , МР   2504193
• Кэннон, Джон Дж. (1969), «Компьютеры в теории групп: обзор», Communications of the ACM , 12 : 3–12, doi : 10.1145/362835.362837 , MR   0290613 , S2CID   18226463
• Фрухт, Р. (1939), «Подготовка графов с заданной абстрактной группой» , Compositio Mathematica , 6 : 239–50, ISSN   0010-437X , заархивировано из оригинала 1 декабря 2008 г.
• Голубицкий, Мартин ; Стюарт, Ян (2006), «Нелинейная динамика сетей: группоидный формализм», Bull. амер. Математика. Соц. (NS) , 43 (3): 305–364, doi : 10.1090/S0273-0979-06-01108-6 , MR   2223010 Показывает преимущество обобщения от группы к группоиду .
• Джадсон, Томас В. (1997), Абстрактная алгебра: теория и приложения. Вводный учебник для студентов в духе текстов Галлиана или Херштейна, охватывающий группы, кольца, области целостности, поля и теорию Галуа. Бесплатно загружаемый PDF-файл с GFDL с открытым исходным кодом. лицензией
• Кляйнер, Израиль (1986), «Эволюция теории групп: краткий обзор», Mathematics Magazine , 59 (4): 195–215, doi : 10.2307/2690312 , ISSN   0025-570X , JSTOR   2690312 , MR   0863090
• Ла Арп, Пьер де (2000), Темы геометрической теории групп , University of Chicago Press , ISBN  978-0-226-31721-2
• Ливио, М. (2005), Уравнение, которое невозможно решить: как математический гений открыл язык симметрии , Саймон и Шустер, ISBN  0-7432-5820-7 Передает практическую ценность теории групп, объясняя, как она указывает на симметрию в физике и других науках.
• Мамфорд, Дэвид (1970), абелевы разновидности , Oxford University Press , ISBN  978-0-19-560528-0 , OCLC   138290
• Ронан М. , 2006. Симметрия и монстр . Издательство Оксфордского университета. ISBN   0-19-280722-6 . Для непрофессиональных читателей. Описывает поиск основных строительных блоков для конечных групп.
• Ротман, Джозеф (1994), Введение в теорию групп , Нью-Йорк: Springer-Verlag, ISBN.  0-387-94285-8 Стандартный современный справочник.
• Шупп, Пол Э .; Линдон, Роджер К. (2001), Комбинаторная теория групп , Берлин, Нью-Йорк: Springer-Verlag , ISBN  978-3-540-41158-1
• Скотт, WR (1987) [1964], Теория групп , Нью-Йорк: Дувр, ISBN  0-486-65377-3 Недорогой и довольно читаемый, но несколько устаревший по акценту, стилю и обозначениям.
• Шац, Стивен С. (1972), Проконечные группы, арифметика и геометрия , Princeton University Press , ISBN  978-0-691-08017-8 , МР   0347778
• Вейбель, Чарльз А. (1994), Введение в гомологическую алгебру , Кембриджские исследования по высшей математике, том. 38, Издательство Кембриджского университета, ISBN  978-0-521-55987-4 , МР   1269324 , OCLC   36131259

Внешние ссылки

• История концепции абстрактной группы
• Теория групп более высокой размерности. Здесь представлен взгляд на теорию групп как на первый уровень теории, которая распространяется во всех измерениях и имеет приложения в теории гомотопий и к неабелевым методам более высокой размерности для решения локально-глобальных задач.
• Пакет Plus для учителей и студентов: Теория групп В этом пакете собраны все статьи по теории групп из Plus , онлайн-журнала по математике, выпускаемого в рамках проекта Millennium Mathematics Project в Кембриджском университете, в котором рассматриваются приложения и недавние открытия, а также приводятся подробные определения и примеры группы.
• Бернсайд, Уильям (1911), «Группы, теория» , в Чисхолме, Хью (редактор), Британская энциклопедия , том. 12 (11-е изд.), Cambridge University Press, стр. 626–636. Это подробное изложение современного понимания теории групп одним из первых исследователей в этой области.