Математика и искусство

Это хорошая статья. Для получения дополнительной информации нажмите здесь.
Из Википедии, бесплатной энциклопедии

Математика в искусстве: Альбрехта Дюрера гравюра на медной пластине «Меленхолия I» , 1514 год. Математические ссылки включают циркуль для геометрии , магический квадрат и усеченный ромбоэдр , а измерения указываются с помощью весов и песочных часов . [1]
Каркасный рисунок [2] вазы как тела вращения [2] Паоло Уччелло . 15 век
Часть серии о
Математика
Области
Связь с науками
Математический портал

Математика и искусство связаны по-разному. Математику называют искусством, движимым красотой . Математику можно обнаружить в таких видах искусства, как музыка , танец , живопись , архитектура , скульптура и текстиль . Однако эта статья посвящена математике в изобразительном искусстве.

Математика и искусство имеют давнюю историческую связь. Художники использовали математику с 4-го века до нашей эры, когда греческий скульптор Поликлет написал свой Канон , предписывая пропорции, предположительно основанные на соотношении 1: √ 2 для идеального обнаженного мужчины. Настойчивые популярные утверждения об использовании золотого сечения в древнем искусстве и архитектуре без надежных доказательств. итальянского Возрождения В эпоху Лука Пачоли написал влиятельный трактат «О божественной пропорции» (1509), иллюстрированный гравюрами на дереве Леонардо да Винчи , об использовании золотого сечения в искусстве. Другой итальянский художник, Пьеро делла Франческа , развил перспективе идеи Евклида о в таких трактатах, как « De Prospectiva Pingendi» , и в своих картинах. Гравер Альбрехт Дюрер много раз ссылался на математику в своей работе «Меланхолия I» . В наше время художник-график М. К. Эшер интенсивно использовал мозаику и гиперболическую геометрию с помощью математика Х. С. М. Коксетера , а Движение Де Стиджа , возглавляемое Тео ван Дусбургом и Питом Мондрианом, открыто придерживалось геометрических форм. Математика вдохновила такие текстильные искусства, как лоскутное шитье , вязание , вышивка крестиком , вязание крючком , вышивка , ткачество , изготовление турецких и других ковров , а также килим . В исламском искусстве симметрия проявляется в таких разнообразных формах, как персидский гирих и марокканская плитка зеллиге , каменные ширмы с пронзенными могольскими джали и широко распространенные своды мукарнас .

Математика напрямую повлияла на искусство благодаря концептуальным инструментам, таким как линейная перспектива , анализ симметрии и математическим объектам, таким как многогранники и лента Мёбиуса . Магнус Веннингер создает красочные звездчатые многогранники , первоначально как модели для обучения. Математические концепции, такие как рекурсия и логический парадокс, можно увидеть на картинах Рене Магритта и гравюрах М.К. Эшера. Компьютерное искусство часто использует фракталы , включая множество Мандельброта , а иногда исследует другие математические объекты, такие как клеточные автоматы . Вызывает споры то, что художник Дэвид Хокни утверждал, что художники, начиная с эпохи Возрождения, использовали камеру-люциду для точного изображения сцен; Архитектор Филип Стедман также утверждал, что Вермеер использовал камеру-обскуру в своих характерных картинах.

Другие связи включают алгоритмический анализ произведений искусства с помощью рентгеновской флуоресцентной спектроскопии , открытие того, что традиционные батики из разных регионов Явы имеют различные фрактальные измерения , а также стимулы для математических исследований, особенно Филиппо Брунеллески теории перспективы , которая в конечном итоге привела к Жирару. Дезарга геометрия Проективная . Устойчивая точка зрения, основанная в конечном счете на пифагорейском представлении о гармонии в музыке, утверждает, что все организовано числом, что Бог является геометром мира и что, следовательно, геометрия мира священна .

Истоки: от Древней Греции до эпохи Возрождения [ править ]

Дополнительная информация: Художественные каноны пропорций тела.

Поликлета Канон и симметрия ​ ​ ​

Римская мраморная копия Дорифора , первоначально бронзовая работа Поликлета.
Дополнительная информация: Поликлет.

Поликлет Старший (ок. 450–420 до н. э.) — греческий скульптор школы Аргоса , современник Фидия . Его работы и статуи состояли в основном из бронзы и изображали спортсменов. По словам философа и математика Ксенократа , Поликлет считается одним из самых важных скульпторов классической античности за его работу над Дорифором и статуей Геры в Герайоне Аргоса . [3] Хотя его скульптуры, возможно, не так известны, как скульптуры Фидия, они вызывают большое восхищение. В своем «Каноне» , трактате, который он написал, призванном документировать «идеальные» пропорции тела обнаженного мужчины, Поликлет предлагает нам математический подход к скульптурированию человеческого тела. [3]

Сам Канон утерян , но предполагается, что Поликлет использовал последовательность пропорций, в которой каждая длина равна длине диагонали квадрата, нарисованного на его предшественнике, 1: √ 2 (около 1:1,4142). [4]

Влияние Канона Поликлета огромно в классической греческой , римской скульптуре и скульптуре эпохи Возрождения , причем многие скульпторы следовали рецепту Поликлета. Хотя ни одна из оригинальных работ Поликлета не сохранилась, римские копии демонстрируют его идеал физического совершенства и математической точности. Некоторые ученые утверждают, что пифагорейская мысль повлияла на Канон Поликлета. [5] Канон (по-гречески «гармоничные пропорции») , применяет основные математические понятия греческой геометрии, такие как соотношение, пропорция и симметрия и превращает их в систему, способную описывать человеческую форму посредством серии непрерывных геометрических прогрессий . [4]

Перспектива и пропорция [ править ]

Основная статья: Перспектива (графическая)
линейной Эксперимент Брунеллески с перспективой.

В классические времена вместо того, чтобы уменьшать отдаленные фигуры с помощью линейной перспективы , художники определяли размеры объектов и фигур в соответствии с их тематической значимостью. В средние века некоторые художники использовали обратную перспективу для особого акцента . Мусульманский математик Альхазен (Ибн аль-Хайсам) описал теорию оптики в своей «Книге оптики» в 1021 году, но никогда не применял ее к искусству. [6] В эпоху Возрождения произошло возрождение классической греческой и римской культуры и идей, в том числе изучение математики для понимания природы и искусства . Два основных мотива побуждали художников позднего средневековья и эпохи Возрождения обращаться к математике. Сначала живописцам нужно было придумать, как изображать трехмерные сцены на двухмерном холсте. Во-вторых, и философы, и художники были убеждены, что математика является истинной сущностью физического мира и что всю Вселенную, включая искусство, можно объяснить в геометрических терминах. [7]

Зачатки перспективы появились у Джотто (1266/7 – 1337), который пытался нарисовать перспективу, используя алгебраический метод, чтобы определить расположение удаленных линий. В 1415 году итальянский архитектор Филиппо Брунеллески и его друг Леон Баттиста Альберти продемонстрировали во Флоренции геометрический метод применения перспективы, используя подобные треугольники , сформулированные Евклидом, для определения видимой высоты удаленных объектов. [8] [9] Перспективные картины Брунеллески утеряны, но картина Мазаччо , изображающая Святую Троицу, показывает его принципы в действии. [6] [10] [11]

Паоло Уччелло новаторски использовал перспективу в «Битве при Сан-Романо» (ок. 1435–1460).

Итальянский художник Паоло Уччелло (1397–1475) был очарован перспективой, как это показано на его картинах « Битва при Сан-Романо» (ок. 1435–1460): сломанные копья удобно лежат вдоль линий перспективы. [12] [13]

Художник Пьеро делла Франческа (ок. 1415–1492) продемонстрировал этот новый сдвиг в мышлении итальянского Возрождения. Он был опытным математиком и геометром , писал книги по твердотельной геометрии и перспективе , в том числе Despectiva pingendi (О перспективе для живописи) , Trattato d'Abaco (Трактат о счетах) и De quinque corporibus Regularibus (О пяти правильных твердых телах) . [14] [15] [16] Историк Вазари в своих «Жизнеописаниях художников» называет Пьеро «величайшим геометром своего времени, а возможно, и всех времен». [17] Интерес Пьеро к перспективе можно увидеть в его картинах, включая «Полиптих Перуджи» , [18] алтарь Сан-Агостино и «Бичевание Христа» . Его работы по геометрии оказали влияние на более поздних математиков и художников, включая Луку Пачоли в его «Божественной пропорции» и Леонардо да Винчи . Пьеро изучал классическую математику и труды Архимеда . [19] Его обучали коммерческой арифметике в «школах счетов»; его сочинения отформатированы как школьные учебники по счетам, [20] возможно, включая » Леонардо Пизано ( Фибоначчи ) 1202 года «Liber Abaci . Линейная перспектива только-только внедрялась в художественный мир. Альберти объяснил в своей книге «De pictura » 1435 года : «лучи света движутся по прямым линиям от точек наблюдаемой сцены к глазу, образуя своего рода пирамиду с глазом в качестве вершины». Картина, построенная с линейной перспективой, представляет собой поперечное сечение этой пирамиды. [21]

В «De Prospectiva Pingendi » Пьеро преобразует свои эмпирические наблюдения за тем, как аспекты фигуры меняются с точки зрения, в математические доказательства. Его трактат начинается в духе Евклида: он определяет точку как «мельчайшую вещь, которую может постичь глаз». [а] [7] Он использует дедуктивную логику , чтобы привести читателя к перспективному изображению трехмерного тела. [22]

Художник Дэвид Хокни утверждал в своей книге «Тайное знание: заново открывая утраченные техники старых мастеров» , что художники начали использовать камеру-люциду с 1420-х годов, что привело к внезапному изменению точности и реализма, и что эту практику продолжили крупные художники, в том числе Энгр , Ван Эйк и Караваджо . [23] Критики расходятся во мнениях относительно того, был ли Хокни прав. [24] [25] Точно так же архитектор Филип Стедман спорно утверждал. [26] что Вермеер использовал другое устройство, камеру-обскуру , чтобы создавать свои характерные картины. [27]

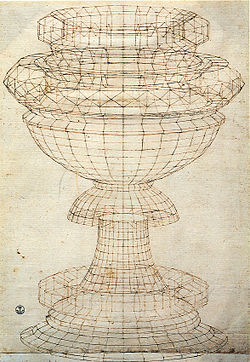
В 1509 году Лука Пачоли (ок. 1447–1517) опубликовал книгу «De divinaпропорция» о математических и художественных пропорциях , в том числе в человеческом лице. Леонардо да Винчи (1452–1519) иллюстрировал текст гравюрами на дереве из твердых тел правильной формы, когда учился у Пачоли в 1490-х годах. Рисунки Леонардо, вероятно, являются первыми иллюстрациями скелетных тел. [28] Они, такие как ромбокубооктаэдр , были одними из первых, которые были нарисованы для демонстрации перспективы путем наложения друг на друга. В работе рассматривается перспектива в творчестве Пьеро делла Франческа , Мелоццо да Форли и Марко Пальмеццано . [29] Пачоли Леонардо изучал «Сумму» , из которой он скопировал таблицы пропорций. [30] В «Моне Лизе» и «Тайной вечере» работы Леонардо включали линейную перспективу с точкой схода , чтобы обеспечить видимую глубину. [31] «Тайная вечеря» построена в строгом соотношении 12:6:4:3, как и Рафаэля » « Афинская школа , в которой Пифагор изображен с табличкой идеальных соотношений, священной для пифагорейцев. [32] [33] В «Витрувианском человеке » Леонардо выразил идеи римского архитектора Витрувия , новаторски дважды показав мужскую фигуру и сосредоточив ее как в круге, так и в квадрате. [34]

Еще в 15 веке криволинейная перспектива нашла свое отражение в картинах художников, интересующихся искажениями изображений. » Яна ван Эйка 1434 года На «Портрете Арнольфини есть выпуклое зеркало с отражениями людей на сцене. [35] в то время как Автопортрет Пармиджанино « в выпуклом зеркале» , ок. 1523–1524 гг.: в центре изображено почти неискаженное лицо художника, с сильно изогнутым фоном и рукой художника по краю. [36]

Трехмерное пространство можно убедительно представить в искусстве, как и в техническом рисунке , не только перспективой, но и другими средствами. Косые проекции , в том числе кавалерийская перспектива (использовавшаяся французскими военными художниками для изображения укреплений в 18 веке), постоянно и повсеместно использовались китайскими художниками с первого или второго веков до 18 века. Китайцы переняли эту технику из Индии, которая заимствовала ее из Древнего Рима. Косая проекция встречается в японском искусстве, например, в укиё-э картинах Тории Киёнаги (1752–1815). [37]

Золотое сечение [ править ]

Дополнительная информация: Список работ, созданных с использованием золотого сечения.

Золотое сечение (примерно равное 1,618) было известно еще Евклиду . [38] Золотое сечение постоянно утверждается [39] [40] [41] [42] в наше время использовался в искусстве и архитектуре древними в Египте, Греции и других странах без надежных доказательств. [43] Это утверждение может быть связано с путаницей с «золотой серединой», которая для древних греков означала «избегание излишеств в любом направлении», а не соотношение. [43] Пирамидологи с 19-го века приводили доводы в пользу сомнительного математического обоснования золотого сечения в конструкции пирамид. [б] , Утверждается, что Парфенон храм V века до нашей эры в Афинах, использует золотое сечение в своем фасаде и плане этажа. [47] [48] [49] но и эти утверждения опровергаются измерениями. [43] сечение . Утверждается, что и Великая мечеть Кайруан в Тунисе использует в своем дизайне золотое [50] но это соотношение не проявляется в первоначальных частях мечети. [51] Историк архитектуры Фредерик Макоди Лунд утверждал в 1919 году, что Шартрский собор (12 век), Нотр-Дам в Лаоне (1157–1205) и Нотр-Дам де Пари (1160) спроектированы в соответствии с золотым сечением. [52] рисуя линии регулятора, чтобы обосновать свою позицию. Другие ученые утверждают, что до работы Пачоли в 1509 году золотое сечение было неизвестно художникам и архитекторам. [53] Например, высота и ширина фасада Нотр-Дама в Лаоне имеют соотношение 8/5 или 1,6, а не 1,618. Такие соотношения Фибоначчи быстро становится трудно отличить от золотого сечения. [54] После Пачоли золотое сечение более отчетливо заметно в произведениях искусства, включая « Мону Лизу » Леонардо . [55]

Другое соотношение, единственное другое морфическое число, [56] был назван пластиковым номером [с] в 1928 году голландский архитектор Ханс ван дер Лаан (первоначально называвшийся по-французски le nombre radiant ). [57] Его значение является решением кубического уравнения

,

иррациональное число, равное приблизительно 1,325. По мнению архитектора Ричарда Падована , это имеет характерные соотношения. 3/4 ​ ​ и 1/7 которые , определяют пределы человеческого восприятия при соотнесении одного физического размера с другим. Ван дер Лаан использовал эти соотношения при проектировании церкви аббатства Св. Бенедиктусберга в Нидерландах в 1967 году. [57]

Плоские симметрии [ править ]

Дополнительная информация: Плоская симметрия , группа обоев , исламские геометрические узоры и килим.
Мощное присутствие: [58] ковер с двойным медальоном. Центральная Анатолия (Конья – Карапынар), рубеж 16-17 веков. Мечеть Алаеддина

Плоские симметрии на протяжении тысячелетий использовались в таких произведениях искусства, как ковры , решетки, текстиль и плитка. [59] [60] [61] [62]

Многие традиционные ковры, будь то ворсовые ковры или килимы плоского переплетения , разделены на центральное поле и обрамляющую границу; оба могут иметь симметрию, хотя в коврах ручной работы она часто слегка нарушается мелкими деталями, вариациями рисунка и изменениями цвета, внесенными ткачом. [59] В килимах из Анатолии обычно используемые мотивы симметричны. Общая компоновка также обычно присутствует, с такими расположениями, как полосы, полосы, чередующиеся с рядами мотивов, и упакованные массивы примерно шестиугольных мотивов. Поле обычно оформляется в виде обоев с группой обоев, такой как pmm, а граница может располагаться в виде фриза из группы фризов pm11, pmm2 или pma2. Турецкие и среднеазиатские килимы часто имеют три и более каймы в разных группах фризов. Ткачи определенно стремились к симметрии, не имея явных знаний ее математики. [59] Математик и теоретик архитектуры Никос Салингарос предполагает, что «мощное присутствие» [58] (эстетический эффект) «большого ковра» [58] такие как лучшие ковры с двумя медальонами Коньи 17 века, созданы с помощью математических методов, связанных с теориями архитектора Кристофера Александера . Эти методы включают в себя создание пары противоположностей; противоположные цветовые значения; геометрическое разграничение областей, используя дополнительные формы или балансируя направленность острых углов; обеспечение мелкомасштабной сложности (от уровня узла вверх) и как мелкомасштабной, так и крупномасштабной симметрии; повторяющиеся элементы в иерархии разного масштаба (с соотношением примерно 2,7 от каждого уровня к следующему). Салингарос утверждает, что «все успешные ковры удовлетворяют как минимум девяти из десяти вышеперечисленных правил», и предполагает, что на основе этих правил можно было бы создать метрику. [58]

Сложные решетки встречаются в работах индийского Джали , вырезанные из мрамора и украшающие гробницы и дворцы. [60] Китайские решетки, всегда обладающие некоторой симметрией, присутствуют в 14 из 17 групп обоев; они часто имеют зеркальную, двойную зеркальную или вращательную симметрию. Некоторые имеют центральный медальон, а некоторые имеют окантовку в группе фризов. [63] Многие китайские решетки были математически проанализированы Дэниелом С. Даем; он называет Сычуань центром ремесла. [64]

Плитка Гирих

Симметрии широко распространены в текстильном искусстве, включая лоскутное шитье , [61] Вязание , [65] вышивка крестиком , крючком , [66] вышивка [67] [68] и плетение , [69] где они могут носить чисто декоративный характер или быть признаком статуса. [70] Вращательная симметрия встречается в круглых структурах, таких как купола ; иногда они тщательно украшены симметричными узорами внутри и снаружи, как, например, в мечети шейха Лотфоллы 1619 года в Исфахане . [71] Предметы вышивки и кружева , такие как скатерти и скатерти, изготовленные с использованием коклюшек или фриволите , могут иметь широкий спектр отражательной и вращательной симметрии, которые исследуются математически. [72]

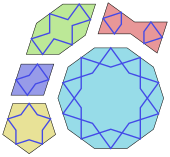
Исламское искусство использует симметрию во многих своих формах искусства, особенно в мозаике гирих . Они сформированы с использованием набора из пяти форм плитки, а именно правильного десятиугольника, вытянутого шестиугольника, галстука-бабочки, ромба и правильного пятиугольника. Все стороны этих плиток имеют одинаковую длину; и все их углы кратны 36 ° (π/5 радиан ), что обеспечивает пятикратную и десятикратную симметрию. Плитки украшены полосками (гирих), которые обычно более заметны, чем границы плитки. В 2007 году физики Питер Лу и Пол Стейнхардт утверждали, что гирих напоминает квазикристаллические мозаики Пенроуза . [73] Сложная геометрическая плитка zellige — отличительный элемент марокканской архитектуры. [62] Своды Мукарнаса трехмерны, но были спроектированы в двух измерениях с рисунками геометрических ячеек. [74]

Многогранники [ править ]

Платоновые тела и другие многогранники — постоянная тема в западном искусстве. Они встречаются, например, в мраморной мозаике с изображением небольшого звездчатого додекаэдра , приписываемой Паоло Уччелло, на полу базилики Сан-Марко в Венеции; [12] в схемах правильных многогранников Леонардо да Винчи, нарисованных в качестве иллюстраций к книге Луки Пачоли 1509 года «Божественная пропорция» ; [12] как стеклянный ромбокубооктаэдр на портрете Пачоли Якопо де Барбари, написанном в 1495 году; [12] в усеченном многограннике (и различных других математических объектах) на Альбрехта Дюрера гравюре «Меланхолия I» ; [12] и в Сальвадора Дали картине «Тайная вечеря» , на которой Христос и его ученики изображены внутри гигантского додекаэдра . [75]

Альбрехт Дюрер (1471–1528) был немецким эпохи Возрождения гравером , который внес важный вклад в многогранную литературу в своей книге 1525 года Underweysung der Messung (Образование в области измерений) , призванной преподавать предметы линейной перспективы , геометрии в архитектуре , платоновых тел и правильные многоугольники . Дюрер, вероятно, находился под влиянием работ Луки Пачоли и Пьеро делла Франческа во время своих поездок в Италию . [76] Хотя примеры перспективы в «Underweysung der Messung» недостаточно развиты и содержат неточности, многогранники подробно обсуждаются. Дюрер также первым представил в тексте идею многогранных сеток — многогранников, развернутых так, чтобы они лежали ровно для печати. [77] Дюрер опубликовал еще одну влиятельную книгу о человеческих пропорциях под названием Vier Bücher von Menschlicher Proportion («Четыре книги о человеческих пропорциях») . В 1528 году [78]

Известная гравюра Дюрера «Меленхолия I» изображает разочарованного мыслителя, сидящего возле усеченного треугольного трапецоэдра и магического квадрата . [1] Эти два объекта и гравюра в целом стали предметом более современной интерпретации, чем содержание практически любой другой гравюры. [1] [79] [80] включая двухтомную книгу Питера-Клауса Шустера, [81] и влиятельная дискуссия в Эрвина Панофски . монографии Дюрера [1] [82]

Сальвадора Дали Картина 1954 года «Гиперкуб тела» уникальным образом изображает крест Христа как развернутую трехмерную сеть гиперкуба , также известного как тессеракт : развертывание тессеракта на эти восемь кубов аналогично развертыванию сторон куба в крестообразная форма из шести квадратов, здесь представляющая божественную перспективу в виде четырехмерного правильного многогранника. [83] [84] На картине изображена фигура Христа перед тессарактом; Обычно его изображают прикрепленным к кресту гвоздями, но на картине гвоздей нет. Вместо этого перед его телом есть четыре маленьких куба, в углах самого переднего из восьми кубов тессаракта. Математик Томас Банчофф утверждает, что Дали пытался выйти за пределы трехмерного мира, а поэт и искусствовед Келли Гровьер говорит, что «картина, кажется, разрушила связь между духовностью спасения Христа и материальностью геометрического и физического мира». силы, кажется, преодолевают разрыв, который, по мнению многих, отделяет науку от религии». [85]

Фрактальные измерения [ править ]

Батики из Суракарты , Ява, как и этот паранг-клитик узор меча , имеют фрактальную размерность от 1,2 до 1,5.

с восковым сопротивлением Традиционные индонезийские рисунки батика на ткани сочетают в себе репрезентативные мотивы (такие как цветочные и растительные элементы) с абстрактными и несколько хаотичными элементами, включая неточность в нанесении воскового резиста и случайные вариации, вызванные растрескиванием воска. Дизайн батика имеет фрактальное измерение от 1 до 2, которое варьируется в разных региональных стилях. Например, батик Чиребона имеет фрактальную размерность 1,1; батики Джокьякарты и Суракарты (Соло) в Центральной Яве имеют фрактальную размерность от 1,2 до 1,5; а батики Ласема на северном побережье Явы и Тасикмалая на Западной Яве имеют фрактальную размерность от 1,5 до 1,7. [86]

Капельная живопись современного художника Джексона Поллока также отличается своим фрактальным измерением. Его «Номер 14» 1948 года имеет размер 1,45, подобный береговой линии, в то время как его более поздние картины имели последовательно более высокие фрактальные размеры и, соответственно, более сложные узоры. На создание одной из его последних работ, « Голубые полюса» , ушло шесть месяцев, и она имеет фрактальную размерность 1,72. [87]

Сложные отношения [ править ]

Астроном Галилео Галилей в своей книге «Саджиаторе» писал, что «[Вселенная] написана на языке математики , а ее символами являются треугольники, круги и другие геометрические фигуры». [88] Художники, которые стремятся и стремятся изучать природу, должны, по мнению Галилея, сначала полностью понять математику. Математики, наоборот, стремились интерпретировать и анализировать искусство через призму геометрии и рациональности. Математик Фелипе Кукер предполагает, что математика, и особенно геометрия, является источником правил для «художественного творчества, основанного на правилах», хотя и не единственным. [89] Некоторые из многих нитей возникающих в результате сложных отношений [90] описаны ниже.

Математик Г.Х. Харди определил ряд критериев математической красоты .

Математика как искусство [ править ]

Основная статья: Математическая красота

Математик Джерри П. Кинг описывает математику как искусство, заявляя, что «ключами к математике являются красота и элегантность, а не скучность и техничность», и что красота является движущей силой математических исследований. [91] Кинг цитирует эссе математика Г.Х. Харди 1940 года «Апология математика» . В нем Харди обсуждает, почему он считает две теоремы классического времени наиболее важными, а именно доказательство Евклида , что существует бесконечно много простых чисел , и доказательство того, что квадратный корень из 2 иррационален . Харди Кинг оценивает это последнее по критериям математической элегантности : « серьезность, глубина, общность, неожиданность, неизбежность и экономия » (курсив Кинга) и описывает доказательство как «эстетичное». [92] Венгерский математик Пауль Эрдеш согласился с тем, что математика обладает красотой, но рассматривал причины, не поддающиеся объяснению: «Почему числа прекрасны? Это все равно, что спрашивать, почему Девятая симфония Бетховена прекрасна. Если вы не понимаете, почему, кто-то не сможет вам сказать. Я знаю цифры прекрасны». [93]

Математические инструменты для искусства [ править ]

Дополнительная информация: Список художников-математиков , фрактального искусства и компьютерного искусства.

Математику можно обнаружить во многих искусствах, таких как музыка , танец , [94] живопись , архитектура и скульптура . Каждый из них тесно связан с математикой. [95] Среди связей с изобразительным искусством математика может предоставить художникам инструменты, такие как правила линейной перспективы , описанные Бруком Тейлором и Иоганном Ламбертом , или методы начертательной геометрии , которые сейчас применяются в программном моделировании твердых тел, восходящие к Альбрехту. Дюрер и Гаспар Монж . [96] Художники Луки Пачоли в средние века , Леонардо да Винчи и Альбрехта Дюрера в эпоху Возрождения использовали и развивали математические идеи в своей художественной работе. [95] [97] Использование перспективы началось, несмотря на некоторые зачаточные ее обычаи в архитектуре Древней Греции, с итальянскими художниками, такими как Джотто, в 13 веке; такие правила, как точка схода, были впервые сформулированы Брунеллески примерно в 1413 году. [6] его теория оказала влияние на Леонардо и Дюрера. Исаака Ньютона Работы по оптическому спектру повлияли на и Гете «Теорию цвета» , в свою очередь, на таких художников, как Филипп Отто Рунге , Дж. М. У. Тёрнер , [98] Прерафаэлиты Василий и Кандинский . [99] [100] Художники также могут проанализировать симметрию сцены. [101] Инструменты могут применяться математиками, изучающими искусство, или художниками, вдохновленными математикой, такими как М. К. Эшер (вдохновленный Х. С. М. Коксетером ) и архитектор Фрэнк Гери , который более сдержанно утверждал, что компьютерное проектирование позволило ему выразить себя в совершенно новом виде. способ. [102]

Осьминог Микаэля Хвидтфельдта Кристенсена. Алгоритмическое искусство , созданное с помощью программного обеспечения Structure Synth.

Художник Ричард Райт утверждает, что математические объекты, которые можно сконструировать, можно рассматривать либо «как процессы моделирования явлений», либо как произведения « компьютерного искусства ». Он рассматривает природу математической мысли, отмечая, что фракталы были известны математикам за столетие до того, как они были признаны таковыми. В заключение Райт заявляет, что уместно подвергать математические объекты любым методам, используемым для «примирения с культурными артефактами, такими как искусство, напряжением между объективностью и субъективностью, их метафорическими значениями и характером репрезентативных систем». В качестве примеров он приводит изображение из множества Мандельброта , изображение, созданное алгоритмом клеточного автомата , и изображение , визуализированное компьютером , и обсуждает, со ссылкой на тест Тьюринга , могут ли алгоритмические продукты быть искусством. [103] В книге Сашо Каладжиевского «Математика и искусство: введение в визуальную математику» используется аналогичный подход, рассматривая подходящие темы визуальной математики, такие как мозаики, фракталы и гиперболическая геометрия. [104]

Некоторые из первых произведений компьютерного искусства были созданы Десмондом Полом Генри «Рисовальная машина 1», аналоговая машина , основанная на компьютере бомбового прицела и выставленная в 1962 году. [105] [106] Машина была способна создавать сложные, абстрактные, асимметричные, криволинейные, но повторяющиеся линейные рисунки. [105] [107] Совсем недавно Хамид Надери Йегане создал формы, напоминающие объекты реального мира, такие как рыбы и птицы, используя формулы, которые последовательно изменялись для рисования семейств кривых или угловых линий. [108] [109] [110] Такие художники, как Микаэль Хвидтфельдт Кристенсен, создают произведения генеративного или алгоритмического искусства , написав сценарии для такой программной системы, как Structure Synth : художник эффективно направляет систему на применение желаемой комбинации математических операций к выбранному набору данных. [111] [112]

От математики к искусству [ править ]

Протокубизм : картина Пабло Пикассо 1907 года «Авиньонские девицы» использует проекцию четвертого измерения , чтобы показать фигуру как в анфас, так и в профиль. [113]
Дополнительная информация: Протокубизм , мозаика , MC Эшер , математика складывания бумаги , а также математика и волоконное искусство.

Книга математика и физика-теоретика Анри Пуанкаре « Наука и гипотеза» была широко прочитана кубистами , в том числе Пабло Пикассо и Жаном Метцингером . [114] [115] Будучи хорошо знаком с работами Бернхарда Римана по неевклидовой геометрии, Пуанкаре более чем осознавал, что евклидова геометрия — это всего лишь одна из многих возможных геометрических конфигураций, а не абсолютная объективная истина. Возможное существование четвертого измерения вдохновило художников усомниться в классической перспективе Возрождения : неевклидова геометрия стала действенной альтернативой. [116] [117] [118] Идея о том, что живопись может быть выражена математически, в цвете и форме, способствовала развитию кубизма, художественного движения, которое привело к абстрактному искусству . [119] Метцингер в 1910 году писал, что: «[Пикассо] излагает свободную, подвижную перспективу, из которой гениальный математик Морис Принсе вывел целую геометрию». [120] Позже Метцингер написал в своих мемуарах:

Морис Принс часто присоединялся к нам... как художник он концептуализировал математику, как эстетик он использовал n -мерные континуумы. Он любил заинтересовывать художников новыми взглядами на космос , открытыми Шлегелем и некоторыми другими. Ему это удалось. [121]

Стремление создавать обучающие или исследовательские модели математических форм естественным образом создает объекты, обладающие симметрией и удивительными или приятными формами. Некоторые из них вдохновили таких художников, как дадаист Ман Рэй , [122] Марсель Дюшан [123] и Макс Эрнст , [124] [125] и вслед за Ман Рэем Хироши Сугимото . [126]

Эннепер появляется как дадаизм : Ман Рэя 1934 года математический объект

Ман Рэй сфотографировал некоторые математические модели Института Анри Пуанкаре в Париже, в том числе Objet Mathematique (Математический объект). Он отметил, что это представляет собой поверхности Эннепера с постоянной отрицательной кривизной , полученные из псевдосферы . Эта математическая основа была для него важна, поскольку позволяла ему отрицать, что объект был «абстрактным», вместо этого утверждая, что он был так же реален, как писсуар, который Дюшан превратил в произведение искусства. Ман Рэй признал, что формула объекта [поверхности Эннепера] «ничего для меня не значила, но сами формы были столь же разнообразны и аутентичны, как и любые другие в природе». Он использовал свои фотографии математических моделей в качестве фигур в своих сериях по пьесам Шекспира , таких как картина 1934 года «Антоний и Клеопатра» . [127] Арт-репортер Джонатан Китс в статье для ForbesLife утверждает, что Ман Рэй фотографировал «эллиптические параболоиды и конические точки в том же чувственном свете, что и его фотографии Кики де Монпарнас », и «гениально перепрофилирует классные математические расчеты, чтобы раскрыть топологию желание". [128] Скульпторы двадцатого века, такие как Генри Мур , Барбара Хепворт и Наум Габо, черпали вдохновение из математических моделей. [129] Мур писал о своей книге « Мать и дитя на струнах» 1938 года : «Несомненно, источником моих струнных фигур был Музей науки … Я был очарован математическими моделями, которые я там видел… Это было не научное исследование этих моделей, а способность смотреть сквозь струны, как через птичью клетку, и видеть одну форму внутри другой, что меня взволновало». [130]

Тео ван Дусбурга , Шесть моментов развития полета самолета в космос 1926 или 1929 гг.

Художники Тео ван Дусбург и Пит Мондриан основали движение Де Стиль , которое они хотели «создать визуальный словарь, состоящий из элементарных геометрических форм, понятных всем и адаптируемых к любой дисциплине». [131] [132] Многие из их работ явно состоят из разлинованных квадратов и треугольников, а иногда и кругов. Художники De Stijl работали в области живописи, мебели, дизайна интерьера и архитектуры. [131] После распада Де Стейла Ван Дусбург основал движение «Авангардное искусство-конкрет» , описав свою «Арифметическую композицию » 1929–1930 годов , серию из четырех черных квадратов по диагонали квадратного фона, как «структуру, которой можно управлять, определенная поверхность без случайных элементов или индивидуального каприза», но «не лишена духа, не лишена всеобщего и не... пуста, поскольку есть все , что соответствует внутреннему ритму». Искусствовед Глэдис Фабр отмечает, что в картине действуют два прогресса: растущие черные квадраты и чередующийся фон. [133]

Математика мозаики , многогранников, формирования пространства и самореференции предоставила художнику-графику М. К. Эшеру (1898–1972) материал на всю жизнь для его гравюр на дереве. [134] [135] В «Наброске Альгамбры» Эшер показал, что искусство можно создавать с помощью многоугольников или правильных форм, таких как треугольники, квадраты и шестиугольники. Эшер использовал неправильные многоугольники при мозаике плоскости и часто использовал отражения, скользящие отражения и перемещения для получения дополнительных узоров. Многие его работы содержат невозможные конструкции, выполненные с использованием геометрических объектов, которые создают противоречие между перспективной проекцией и трехмерностью, но приятны человеческому зрению. Книга Эшера « Восхождение и спуск» основана на « невозможной лестнице », созданной ученым-медиком Лайонелом Пенроузом и его сыном, математиком Роджером Пенроузом . [136] [137] [138]

Некоторые из многочисленных мозаичных рисунков Эшера были вдохновлены беседами с математиком Х.С.М. Коксетером о гиперболической геометрии . [139] Эшера особенно интересовали пять особых многогранников, которые неоднократно встречаются в его работах. Платоновы тела — тетраэдры, кубы, октаэдры, додекаэдры и икосаэдры — особенно заметны в «Порядке и хаосе» и «Четырех правильных телах» . [140] Эти звездчатые фигуры часто находятся внутри другой фигуры, что еще больше искажает угол обзора и форму многогранников и создает многогранное перспективное произведение искусства. [141]

Визуальная сложность математических структур, таких как мозаика и многогранники, вдохновила на создание множества математических произведений. Стюарт Коффин собирает многогранные головоломки в редком и красивом лесу; Джордж Харт работает над теорией многогранников и лепит объекты, вдохновленные ими; Магнус Веннингер делает «особенно красивые» модели сложных звездчатых многогранников . [142]

Искаженные перспективы анаморфозы исследуются в искусстве с шестнадцатого века, когда Ганс Гольбейн Младший включил сильно искаженный череп в свою картину 1533 года « Послы» . С тех пор многие художники, в том числе Эшер, использовали анаморфные приемы. [143]

Математика топологии вдохновила в наше время нескольких художников. Скульптор Джон Робинсон (1935–2007) создал такие работы, как «Гордиев узел» и «Повязки дружбы» , демонстрируя теорию узлов в полированной бронзе. [7] Другие работы Робинсона исследуют топологию торов . Бытие основано на кольцах Борромео – наборе из трех кругов, никакие два из которых не связаны между собой, но в которых всю структуру невозможно разобрать, не разрушив. [144] Скульптор Хеламан Фергюсон создает сложные поверхности и другие топологические объекты . [145] Его работы представляют собой визуальное представление математических объектов; Восьмеричный путь основан на проективной специальной линейной группе PSL(2,7) — конечной группе из 168 элементов. [146] [147] Скульптор Батшеба Гроссман также основывает свою работу на математических структурах. [148] [149] Художник Нельсон Сайерс включает в свое искусство математические концепции и теоремы, от топосов и схем до теоремы о четырех цветах и ​​иррациональности числа π . [150]

Проект исследования гуманитарных наук исследует связи между математикой и искусством с помощью ленты Мёбиуса , флексагонов , оригами и панорамной фотографии. [151]

Математические объекты, включая многообразие Лоренца и гиперболическую плоскость, были созданы с использованием волоконного искусства, в том числе вязания крючком. [д] [153] Американская ткачиха Ада Дитц в 1949 году написала монографию «Алгебраические выражения в тканях ручной работы» , в которой определила схемы ткачества, основанные на разложении многомерных полиномов . [154] Математик Дайна Тайминя продемонстрировала особенности гиперболической плоскости, связав крючком в 2001 году. [155] Это побудило Маргарет и Кристину Вертхайм связать крючком коралловый риф , состоящий из множества морских животных, таких как голожаберники , формы которых основаны на гиперболических плоскостях. [156] Математик Дж. К. П. Миллер использовал « Правило 90» клеточный автомат для создания гобеленов , изображающих как деревья, так и абстрактные узоры из треугольников. [157] «Математики» [158] используют вязаные версии математических объектов, таких как гексафлексагоны Пэт Эшфорт и Стив Пламмер в своем обучении , хотя их губку Менгера оказалось слишком сложно вязать, и вместо нее она была сделана из пластикового холста. [159] [160] Их проект «mathghans» («Афганцы для школ») ввел вязание в британскую учебную программу по математике и технологиям. [161] [162]

Семиотическая шутка: Рене Магритт « Состояние человека» , 1933 г.

Иллюстрирование математики [ править ]

Лицевая сторона , Джотто « Триптиха Стефанески» 1320 год, иллюстрирует рекурсию .
Деталь кардинала Стефанески, держащего триптих.

Моделирование — далеко не единственный возможный способ иллюстрации математических понятий. Джотто «Триптих Стефанески» , 1320 год, иллюстрирует рекурсию в форме мизансцены ; На центральной панели триптиха слева внизу изображена коленопреклоненная фигура кардинала Стефанески, держащего триптих как подношение. [165] картины Джорджо де Кирико, такие Метафизические как его «Великий метафизический интерьер» 1917 года , исследуют вопрос уровней репрезентации в искусстве, изображая картины внутри его картин. [166]

Искусство может служить примером логических парадоксов, как в некоторых картинах сюрреалиста Рене Магритта , которые можно прочитать как семиотические шутки о путанице между уровнями. В «Человеческом состоянии» (1933) Магритт изображает мольберт (на реальном холсте), плавно поддерживающий вид из окна, обрамленного на картине «настоящими» шторами. Эшера Точно так же «Галерея печати» (1956) представляет собой гравюру, изображающую искаженный город, содержащий галерею, рекурсивно содержащую изображение, и так до бесконечности . [167] Магритт использовал сферы и кубоиды, чтобы искажать реальность по-другому, нарисовав их рядом с множеством домов в своей «Ментальной арифметике» 1931 года , как если бы они были детскими строительными блоками, но размером с дом. [168] The Guardian заметила, что «жуткий образ игрушечного города» предсказал узурпацию модернизмом «уютных традиционных форм», но также играет с человеческой склонностью искать закономерности в природе . [169]

Схема очевидного парадокса, воплощенного в литографии Эшера « Галерея печати » 1956 года , обсуждаемая Дугласом Хофштадтером в его книге 1980 года «Гедель, Эшер, Бах». [170]

Последняя картина Сальвадора Дали, «Ласточкин хвост» (1983), была частью серии, вдохновленной Рене Тома теорией катастроф . [171] Испанский художник и скульптор Пабло Паласуэло (1916–2007) сосредоточил внимание на исследовании формы. Он разработал стиль, который назвал геометрией жизни и геометрией всей природы. Состоящий из простых геометрических фигур с детальным рисунком и раскраской, в таких работах, как Angular I и Automnes , Паласуэло выразил себя в геометрических трансформациях. [7]

Художник Адриан Грей практикует балансировку камней , используя трение и центр тяжести для создания поразительных и, казалось бы, невозможных композиций. [172]

Эшера Галерея литографий , г. 1956

Однако художники не обязательно воспринимают геометрию буквально. Как пишет Дуглас Хофштадтер в своем размышлении о человеческом мышлении 1980 года, Гёдель, Эшер, Бах , посредством (помимо прочего) математики искусства: «Разница между рисунком Эшера и неевклидовой геометрией состоит в том, что в последней понятна для неопределенных терминов можно найти интерпретации, в результате чего получается понятная целостная система, тогда как в первом случае конечный результат несовместим с концепцией мира, независимо от того, как долго человек смотрит на картины». Хофштадтер обсуждает, казалось бы, парадоксальную Эшера галерею литографий ; на нем изображен приморский город с художественной галереей, которая, кажется, содержит картину с изображением приморского города, причем на уровнях реальности в изображении существует «странная петля или запутанная иерархия». Самого художника, отмечает Хофштадтер, не видно; его реальность и его отношение к литографии не парадоксальны. [170] Центральная пустота изображения также привлекла интерес математиков Барта де Смита и Хендрика Ленстры , которые предполагают, что она может содержать эффекта Дросте собственную копию , повернутую и сжатую; это было бы еще одной иллюстрацией рекурсии помимо той, которую отметил Хофштадтер. [173] [174]

Анализ истории искусств [ править ]

Алгоритмический анализ изображений произведений искусства, например, с помощью рентгеновской флуоресцентной спектроскопии , может раскрыть информацию об искусстве. Такие методы могут раскрыть изображения в слоях краски, позже покрытых художником; помочь историкам искусства визуализировать произведение искусства до того, как оно треснет или потускнеет; помочь отличить копию от оригинала или отличить стиль мазка мастера от стиля его учеников. [175] [176]

Макс Эрнст делает фигурки Лиссажу , Нью-Йорк, 1942 год.

рисования Джексона Поллока Капельный стиль [177] имеет определенную фрактальную размерность ; [178] среди художников, которые, возможно, повлияли на контролируемый хаос Поллока , [179] Макс Эрнст рисовал фигуры Лиссажу непосредственно, водя проколотым ведром с краской по холсту. [180]

Ученый-компьютерщик Нил Доджсон исследовал, Бриджит Райли можно ли охарактеризовать полосатые картины математически, и пришел к выводу, что, хотя расстояние разделения могло «обеспечить некоторую характеристику», а глобальная энтропия работала на некоторых картинах, автокорреляция не удалась, поскольку узоры Райли были нерегулярными. Локальная энтропия сработала лучше всего и хорошо коррелировала с описанием, данным искусствоведом Робертом Кудиелкой. [181]

» американского математика Джорджа Биркгофа 1933 года В книге «Эстетическая мера предлагается количественная метрика эстетического качества произведения искусства. Он не пытается измерить коннотации произведения, например, что может означать картина, а ограничивается «элементами порядка» многоугольной фигуры. Биркгоф сначала объединяет (как сумму) пять таких элементов: существует ли вертикальная ось симметрии; существует ли оптическое равновесие; сколько у него вращательных симметрий; насколько фигура похожа на обои; и есть ли неудовлетворительные особенности, такие как расположение двух вершин слишком близко друг к другу. Эта метрика O принимает значение от −3 до 7. Вторая метрика C подсчитывает элементы фигуры, что для многоугольника представляет собой количество различных прямых линий, содержащих хотя бы одну из его сторон. Затем Биркгоф определяет свою эстетическую меру красоты объекта как O/C . Это можно интерпретировать как баланс между удовольствием, которое доставляет рассматривание объекта, и количеством усилий, необходимых для его восприятия. Предложение Биркгофа подвергалось различной критике, не в последнюю очередь за попытку выразить красоту в формуле, но он никогда не утверждал, что сделал это. [182]

к исследованиям Стимулы математическим

Дополнительная информация: Проективная геометрия и математика складывания бумаги.

Искусство иногда стимулировало развитие математики, например, когда теория перспективы Брунеллески в архитектуре и живописи положила начало циклу исследований, которые привели к работе Брука Тейлора и Иоганна Генриха Ламберта по математическим основам перспективного рисунка. [183] и, в конечном счете, к математике проективной геометрии Жирара Дезарга и Жана-Виктора Понселе . [184]

Японское искусство складывания бумаги оригами было математически переработано Томоко Фусэ с использованием модулей , конгруэнтных кусочков бумаги, таких как квадраты, и превращения их в многогранники или плитки. [185] Складывание бумаги было использовано в 1893 году Т. Сундара Рао в его «Геометрических упражнениях по складыванию бумаги» для демонстрации геометрических доказательств. [186] Математика складывания бумаги была исследована в теореме Маекавы : [187] Теорема Кавасаки , [188] и аксиомы Хузиты-Хатори . [189]

Иллюзия оп-арта [ править ]

Дополнительная информация: Оп-арт.
Иллюзия спирали Фрейзера , названная в честь сэра Джеймса Фрейзера, открывшего ее в 1908 году.

Оптические иллюзии , такие как спираль Фрейзера, поразительно демонстрируют ограничения человеческого зрительного восприятия, создавая то, что историк искусства Эрнст Гомбрих назвал «непонятным трюком». Черно-белые веревки, которые кажутся образующими спирали, на самом деле являются концентрическими кругами . Оп-арт середины двадцатого века или оптический художественный стиль живописи и графики использовали такие эффекты для создания впечатления движения и мигающих или вибрирующих узоров, которые можно увидеть в работах таких художников, как Бриджит Райли , Спирос Хоремис, [191] и Виктор Вазарели . [192]

Сакральная геометрия [ править ]

Дополнительная информация: Сакральная геометрия , математика и музыка.

В одном из направлений искусства, начиная с Древней Греции, Бог рассматривается как геометр мира, и поэтому геометрия мира считается священной. Вера в то, что Бог создал Вселенную по геометрическому плану, имеет древнее происхождение. Плутарх приписал это убеждение Платону , написав, что «Платон говорил, что Бог постоянно геометризирует» ( Convivialium disputationum , liber 8,2). С тех пор этот образ оказал влияние на западную мысль. Платоновская концепция, в свою очередь, произошла от пифагорейского представления о гармонии в музыке, где ноты располагались в идеальных пропорциях, соответствующих длине струн лиры; действительно, пифагорейцы считали, что все организовано числом. Точно так же в платоновской мысли правильные или Платоновые тела диктуют пропорции, встречающиеся в природе и искусстве. [193] [194] Иллюминация в Виндобонском кодексе XIII века показывает, как Бог рисует вселенную с помощью циркуля, что может отсылать к стиху из Ветхого Завета: «Когда он утвердил небеса, я был там: когда он положил циркуль на лицо из бездны» (Притчи 8:27). [195] В 1596 году астроном-математик Иоганн Кеплер смоделировал Вселенную как набор вложенных друг в друга платоновых тел, определив относительные размеры орбит планет. [195] В произведении Уильяма Блейка « Ветхий днями» (изображающем Уризена , воплощение Блейка разума и закона) и в его картине физика Исаака Ньютона , обнаженного, сгорбленного и рисующего циркулем, символика циркуля используется для критики обычного разума и материализма как узкого. настроенный. [196] [197] На картине Сальвадора Дали 1954 года «Распятие» (Corpus Hypercubus) крест изображен как гиперкуб , представляющий божественную перспективу с четырьмя измерениями, а не с обычными тремя. [84] В картине Дали «Таинство Тайной Вечери» (1955) Христос и его ученики изображены внутри гигантского додекаэдра . [198]

См. также [ править ]

Примечания [ править ]

  1. ^ По-итальянски Пьеро: «что-то настолько пихолиновое, насколько это возможно понять глазом».
  2. ^ Отношение наклонной высоты к половине длины основания составляет 1,619, что составляет менее 1% от золотого сечения, что предполагает использование треугольника Кеплера (угол грани 51 ° 49 '). [43] [44] Однако другие коэффициенты находятся в пределах ошибки измерения той же формы, и исторические данные свидетельствуют о том, что с большей вероятностью использовались простые целочисленные коэффициенты. [45] [46]
  3. ^ « Пластиком » названа способность принимать выбранную трехмерную форму.
  4. ↑ Изображения и видео Хинке Осинги попали в новости международного телевидения, что можно увидеть на связанном веб-сайте. связанного крючком многообразия Лоренца [152]
  5. ↑ Морис Принс подарил копию Пабло Пикассо , чьи альбомы для рисования «Авиньонских девиц» иллюстрируют влияние Жуффре. [114] [164]

Ссылки [ править ]

  1. ^ Перейти обратно: а б с д Циглер, Гюнтер М. (3 декабря 2014 г.). «Многогранник Дюрера: 5 теорий, объясняющих безумный куб Меленхолии» . Хранитель . Проверено 27 октября 2015 г.
  2. ^ Перейти обратно: а б Коломбо, К.; Дель Бимбо, А.; Перничи, Ф. (2005). «Метрическая 3D-реконструкция и получение текстур поверхностей вращения с одного некалиброванного вида». Транзакции IEEE по анализу шаблонов и машинному интеллекту . 27 (1): 99–114. CiteSeerX   10.1.1.58.8477 . дои : 10.1109/TPAMI.2005.14 . ПМИД   15628272 . S2CID   13387519 .
  3. ^ Перейти обратно: а б Стюарт, Эндрю (ноябрь 1978 г.). «Поликлет из Аргоса, «Сто греческих скульпторов: их карьера и дошедшие до нас произведения». эллинистических исследований . 98 : 122–131. doi : 10.2307/630196 . JSTOR   630196. 162410725 S2CID   . Журнал
  4. ^ Перейти обратно: а б Тобин, Ричард (октябрь 1975 г.). « Канон Поликлета». Американский журнал археологии . 79 (4): 307–321. дои : 10.2307/503064 . JSTOR   503064 . S2CID   191362470 .
  5. ^ Рэйвен, Дж. Э. (1951). «Поликлит и пифагореизм». Классический ежеквартальный журнал . 1 (3–4): 147–. дои : 10.1017/s0009838800004122 . S2CID   170092094 .
  6. ^ Перейти обратно: а б с О'Коннор, Джей-Джей; Робертсон, EF (январь 2003 г.). «Математика и искусство – перспектива» . Университет Сент-Эндрюс . Проверено 1 сентября 2015 г.
  7. ^ Перейти обратно: а б с д Эммер, Мишель, изд. (2005). Визуальный разум II . МТИ Пресс. ISBN  978-0-262-05048-7 .
  8. ^ Вазари, Джорджо (1550). Жизнь художников . Торрентино. п. Глава о Брунеллески.
  9. ^ Альберти, Леон Баттиста ; Спенсер, Джон Р. (1956) [1435]. О живописи . Издательство Йельского университета.
  10. ^ Филд, СП (1997). Изобретение бесконечности: математика и искусство эпохи Возрождения . Издательство Оксфордского университета. ISBN  978-0-19-852394-9 .
  11. ^ Уиткомб, Кристофер LCE «Ресурсы по истории искусства» . Проверено 5 сентября 2015 г.
  12. ^ Перейти обратно: а б с д Это Харт, Джордж В. «Многогранники в искусстве» . Проверено 24 июня 2015 г.
  13. ^ Каннингем, Лоуренс; Райх, Джон; Фихнер-Ратус, Лоис (1 января 2014 г.). Культура и ценности: обзор западных гуманитарных наук . Cengage Обучение. п. 375. ИСБН  978-1-285-44932-6 . которые иллюстрируют увлечение Уччелло перспективой. Соревнующиеся бойцы сражаются на поле боя, усеянном сломанными копьями, которые упали почти в виде сетки и направлены в точку схода где-то вдалеке.
  14. ^ делла Франческа, Пьеро (1942) [ок. 1474]. Дж. Никко Фасола (ред.). О перспективной живописи . Флоренция {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
  15. ^ делла Франческа, Пьеро (1970) [Пятнадцатый век]. Дж. Арриги (ред.). Трактат о счетах . Пиза. {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
  16. ^ делла Франческа, Пьеро (1916). Дж. Манчини (ред.). Опера «Регулярное тело» Пьетро Франчески, посвященная узурпации Франчески да Фра Лука Пачоли .
  17. ^ Вазари, Джорджо (1878). Дж. Миланези (ред.). Произведения, том 2 . п. 490.
  18. ^ Зуффи, Стефано (1991). Пьеро делла Франческа . Отделение – Мондадори Арте. п. 53 .
  19. ^ Хит, TL (1908). Тринадцать книг «Начал» Евклида . Издательство Кембриджского университета. п. 97 .
  20. ^ Грендлер, П. (1995). «Чему Пьеро научился в школе: народное образование пятнадцатого века». В М. А. Лавине (ред.). Пьеро делла Франческа и его наследие . Университетское издательство Новой Англии. стр. 161–176.
  21. ^ Альберти, Леон Баттиста ; Грейсон, Сесил (пер.) (1991). Кемп, Мартин (ред.). О живописи . Классика пингвинов.
  22. ^ Петерсон, Марк. «Геометрия Пьеро делла Франческа» . В книге I, после некоторых элементарных построений, призванных представить идею о том, что видимый размер объекта на самом деле является его углом, стянутым в глазу, и ссылаясь на книги I и VI «Начала» Евклида и «Оптику» Евклида, он обращается в предложении 13 к изображение квадрата, лежащего на земле перед зрителем. Что на самом деле должен нарисовать художник? После этого объекты строятся в квадрате (например, плитка для изображения кафельного пола) и соответствующие объекты строятся в перспективе; в Книге II над этими плоскими объектами воздвигаются призмы, обозначающие дома, колонны и т. д.; но основой метода является исходный квадрат, из которого следует все остальное.
  23. ^ Хокни, Дэвид (2006). Тайное знание: открытие утраченных техник старых мастеров . Темза и Гудзон. ISBN  978-0-500-28638-8 .
  24. ^ Ван Рипер, Фрэнк. «Ясная бомба Хокни в художественном заведении» . Вашингтон Пост . Проверено 4 сентября 2015 г.
  25. ^ Марр, Эндрю (7 октября 2001 г.). «То, чего не видел глаз» . Хранитель . Проверено 4 сентября 2015 г.
  26. ^ Янсон, Джонатан (25 апреля 2003 г.). «Интервью с Филипом Стедманом» . Незаменимый Вермеер . Проверено 5 сентября 2015 г.
  27. ^ Стедман, Филип (2002). Камера Вермеера: раскрытие истины, скрывающейся за шедеврами . Оксфорд. ISBN  978-0-19-280302-3 .
  28. ^ Харт, Джордж . «Многогранники Луки Пачоли» . Проверено 13 августа 2009 г.
  29. ^ Моррис, Родерик Конвей (27 января 2006 г.). «Ренессанс Пальмеццано: Из тени выходит художник» . Газета "Нью-Йорк Таймс . Проверено 22 июля 2015 г.
  30. ^ Калтер, Пол. «Геометрия и искусство. Блок 1» . Дартмутский колледж . Проверено 13 августа 2009 г.
  31. ^ Бризио, Анна Мария (1980). Леонардо Художник . МакГроу-Хилл. ISBN  9780070079311 .
  32. ^ Ладвейн, Майкл (2006). Леонардо да Винчи, Тайная вечеря: космическая драма и акт искупления . Издательство Темпл Лодж. стр. 61–62. ISBN  978-1-902636-75-7 .
  33. ^ Тернер, Ричард А. (1992). Изобретение Леонардо . Альфред А. Кнопф. ISBN  9780679415510 .
  34. ^ Волчовер, Натали (31 января 2012 г.). «Леонардо да Винчи скопировал своего знаменитого «Витрувианского человека»?» . Новости Эн-Би-Си . Проверено 27 октября 2015 г.
  35. ^ Криминизи, А.; Кемпц, М.; Канг, С.Б. (2004). «Отражения реальности у Яна ван Эйка и Роберта Кампена» (PDF) . Исторические методы . 37 (3): 109–121. дои : 10.3200/hmts.37.3.109-122 . S2CID   14289312 .
  36. ^ Какер, Фелипе (2013). Многообразные зеркала: пересекающиеся пути искусства и математики . Издательство Кембриджского университета. стр. 299–300, 306–307. ISBN  978-0-521-72876-8 .
  37. ^ Какер, Фелипе (2013). Многообразные зеркала: пересекающиеся пути искусства и математики . Издательство Кембриджского университета. стр. 269–278. ISBN  978-0-521-72876-8 .
  38. ^ Джойс, Дэвид Э. (1996). «Начала Евклида, книга II, предложение 11» . Университет Кларка . Проверено 24 сентября 2015 г.
  39. ^ Сегерс, MJ; Лонгакр, Джей-Джей; Дестефано, Джорджия (1964). «Золотая пропорция и красота». Пластическая и реконструктивная хирургия . 34 (4): 382–386. дои : 10.1097/00006534-196410000-00007 . S2CID   70643014 .
  40. ^ Майнцер, Клаус (1996). Симметрии природы: Справочник по философии природы и науки . Вальтер де Грютер. п. 118.
  41. ^ «Математические свойства в античных театрах и амфитеатрах» . Архивировано из оригинала 15 июля 2017 года . Проверено 29 января 2014 г.
  42. ^ «Архитектура: Эллипс?» . The-Колизей.net . Проверено 29 января 2014 г.
  43. ^ Перейти обратно: а б с д Марковский, Джордж (январь 1992 г.). «Заблуждения о золотом сечении» (PDF) . Математический журнал колледжа . 23 (1): 2–19. дои : 10.2307/2686193 . JSTOR   2686193 . Архивировано из оригинала (PDF) 8 апреля 2008 г. Проверено 26 июня 2015 г.
  44. ^ Тасеос, Сократ Г. (1990). Назад во времени 3104 г. до н. э., к Великой пирамиде . Издательство SOC.
  45. ^ Бартлетт, Кристофер (май 2014 г.). «Проект Великой пирамиды Хуфу» . Сетевой журнал Nexus . 16 (2): 299–311. дои : 10.1007/s00004-014-0193-9 . S2CID   122021107 .
  46. ^ Герц-Фишлер, Роджер (2000). Форма Великой пирамиды . Ватерлоо, Онтарио: Издательство Университета Уилфрида Лорье . ISBN  0-88920-324-5 . МР   1788996 .
  47. ^ Хантли, HE (1970). Божественная пропорция . Дувр.
  48. ^ Хеменвей, Прия (2005). Божественная пропорция: Фи в искусстве, природе и науке . Стерлинг. п. 96.
  49. ^ Усват, Лилиана. «Математика Парфенона» . Журнал «Математика» . Проверено 24 июня 2015 г.
  50. ^ Буссора, Кенза; Мазуз, Саид (весна 2004 г.). «Использование золотого сечения в Великой мечети Кайруана» . Сетевой журнал Nexus . 6 (1): 7–16. дои : 10.1007/s00004-004-0002-y . Геометрическая техника построения золотого сечения, видимо, определила основные решения пространственной организации. Золотое сечение неоднократно появляется в некоторых размерах здания. Это проявляется в общей пропорции плана и размерах молитвенного помещения, двора и минарета. Существование золотого сечения в некоторых частях мечети Кайруан указывает на то, что элементы, спроектированные и созданные с использованием этого принципа, возможно, были реализованы в тот же период.
  51. ^ Бринкворт, Питер; Скотт, Пол (2001). «Место математики». Учитель математики из Австралии . 57 (3): 2.
  52. ^ Чанфон Олмос, Карлос (1991). Курс пропорций. Нормативные процедуры в строительстве . Соглашение об обмене Унам-Уады. Мексика – Мерика.
  53. ^ Ливио, Марио (2002). Золотое сечение: история Фи, самого удивительного числа в мире . Бибкод : 2002grsp.book.....L . ISBN  9780767908160 .
  54. ^ Смит, Норман А.Ф. (2001). «Кафедральные исследования: инженерия или история» (PDF) . Труды Общества Ньюкомена . 73 : 95–137. дои : 10.1179/tns.2001.005 . S2CID   110300481 . Архивировано из оригинала (PDF) 11 декабря 2015 г.
  55. ^ Маквей, Карен (28 декабря 2009 г.). «Почему золотое сечение радует глаз: американский учёный говорит, что знает тайну искусства» . Хранитель . Проверено 27 октября 2015 г.
  56. ^ Аартс, Дж.; Фоккинк, Р.; Крейцер, Г. (2001). «Морфические числа» (PDF) . Новая Арка. Вискд . 5. 2 (1): 56–58.
  57. ^ Перейти обратно: а б Падован, Ричард (2002). Уильямс, Ким; Франсиско Родригес, Хосе (ред.). «Дом Ханс ван дер Лаан и пластиковый номер» . Нексус IV: Архитектура и математика : 181–193.
  58. ^ Перейти обратно: а б с д Салингарос, Никос (ноябрь 1996 г.). «Жизнь ковра: применение правил Александра» . 8-я Международная конференция по восточным коврам . Перепечатано в Эйланд, М.; Пиннер, М., ред. (1998). Восточный ковер и текстильные исследования В . Данвилл, Калифорния: Конференция по восточным коврам.
  59. ^ Перейти обратно: а б с Какер, Фелипе (2013). Многообразные зеркала: пересекающиеся пути искусства и математики . Издательство Кембриджского университета. стр. 89–102. ISBN  978-0-521-72876-8 .
  60. ^ Перейти обратно: а б Лернер, Мартин (1984). Пламя и лотос: искусство Индии и Юго-Восточной Азии из коллекций Кроноса (изд. Каталога выставки). Метрополитен-музей.
  61. ^ Перейти обратно: а б Эллисон, Элейн; Вентерс, Диана (1999). Математические одеяла: шитье не требуется . Ключевой учебный план.
  62. ^ Перейти обратно: а б Кастера, Жан Марк; Перио, Франсуаза (1999). Арабески. Декоративное искусство Марокко . Реализация художественного творчества. ISBN  978-2-86770-124-5 .
  63. ^ Какер, Фелипе (2013). Многообразные зеркала: пересекающиеся пути искусства и математики . Издательство Кембриджского университета. стр. 103–106. ISBN  978-0-521-72876-8 .
  64. ^ Дай, Дэниел С. (1974). Китайские конструкции решеток . Дувр. стр. 30–39 . ISBN  9780486230962 .
  65. ^ Белькастро, Сара-Мари (2013). «Приключения в математическом вязании» . Американский учёный . 101 (2): 124. дои : 10.1511/2013.101.124 .
  66. ^ Таймина, Дайна (2009). Приключения крючком с гиперболическими плоскостями . АК Петерс. ISBN  978-1-56881-452-0 .
  67. ^ Снук, Барбара. Флорентийская вышивка . Скрибнер, второе издание 1967 г.
  68. ^ Уильямс, Эльза С. Барджелло: Работа на флорентийском холсте . Ван Ностранд Рейнхольд, 1967 год.
  69. ^ Грюнбаум, Бранко ; Шепард, Джеффри К. (май 1980 г.). «Атлас и саржа: введение в геометрию тканей». Журнал «Математика» . 53 (3): 139–161. дои : 10.2307/2690105 . hdl : 10338.dmlcz/104026 . JSTOR   2690105 .
  70. ^ Перейти обратно: а б Гамвелл, Линн (2015). Математика и искусство: история культуры . Издательство Принстонского университета. п. 423. ИСБН  978-0-691-16528-8 .
  71. ^ Бейкер, Патрисия Л.; Смит, Хилари (2009). Иран (3-е изд.). Брэдт Путеводители. п. 107. ИСБН  978-1-84162-289-7 .
  72. ^ Ирвин, Вероника; Раски, Фрэнк (2014). «Разработка математической модели кружева на коклюшках». Журнал математики и искусств . 8 (3–4): 95–110. arXiv : 1406.1532 . Бибкод : 2014arXiv1406.1532I . дои : 10.1080/17513472.2014.982938 . S2CID   119168759 .
  73. ^ Лу, Питер Дж.; Стейнхардт, Пол Дж. (2007). «Декагональные и квазикристаллические плитки в средневековой исламской архитектуре». Наука . 315 (5815): 1106–1110. Бибкод : 2007Sci...315.1106L . дои : 10.1126/science.1135491 . ПМИД   17322056 . S2CID   10374218 .
  74. ^ ван ден Хувен, Саския; ван дер Вин, Мартье. «Мукарнас-Математика в исламском искусстве» (PDF) . Архивировано из оригинала (PDF) 27 сентября 2013 года . Проверено 15 января 2016 г.
  75. ^ Марковский, Джордж (март 2005 г.). «Рецензия на книгу: Золотое сечение » (PDF) . Уведомления Американского математического общества . 52 (3): 344–347.
  76. ^ Панофски, Э. (1955). Жизнь и искусство Альбрехта Дюрера . Принстон.
  77. ^ Харт, Джордж В. «Многогранники Дюрера» . Проверено 13 августа 2009 г.
  78. ^ Дюрер, Альбрехт (1528). Сюда включены четыре книги человеческих размеров . Нюрнберг . Проверено 24 июня 2015 г.
  79. ^ Шрайбер, П. (1999). «Новая гипотеза о загадочном многограннике Дюрера в его гравюре на меди «Меленхолия I» » . История Математики . 26 (4): 369–377. дои : 10.1006/hmat.1999.2245 .
  80. ^ Доджсон, Кэмпбелл (1926). Альбрехт Дюрер . Лондон: Общество Медичи. п. 94.
  81. ^ Шустер, Питер Клаус (1991). Меланхолия I: Мысленный образ Дюрера . Берлин: Gebr. Mann Verlag. стр. 17–83.
  82. ^ Панофски, Эрвин ; Клибанский, Раймонд ; Саксль, Фриц (1964). Сатурн и Меланхолия . Основные книги.
  83. ^ Ракер, Руди (2014). Четвертое измерение: к геометрии высшей реальности . Курьерская корпорация. ISBN  978-0-486-79819-6 .
  84. ^ Перейти обратно: а б «Распятие (Corpus Hypercubus)» . Метрополитен-музей . Проверено 5 сентября 2015 г.
  85. ^ Макдональд, Фиона (11 мая 2016 г.). «Художник, вошедший в четвертое измерение» . Би-би-си . Проверено 8 февраля 2022 г.
  86. ^ Лукман, Мухаммед; Хариади, Юн; Дестиарман, Ахмад Халдани (2007). «Фрактальный батик: от традиционного искусства к современной сложности». Proceedings Generative Art X, Милан, Италия .
  87. ^ Уэллетт, Дженнифер (ноябрь 2001 г.). «Фракталы Поллока» . Откройте для себя журнал . Проверено 26 сентября 2016 г.
  88. ^ Галилей, Галилей (1623). Пробирщик . , как переведено на Дрейк, Стиллман (1957). Открытия и мнения Галилея . Даблдэй. стр. 237–238 . ISBN  978-0-385-09239-5 .
  89. ^ Какер, Фелипе (2013). Многообразные зеркала: пересекающиеся пути искусства и математики . Издательство Кембриджского университета. п. 381. ИСБН  978-0-521-72876-8 .
  90. ^ Какер, Фелипе (2013). Многообразные зеркала: пересекающиеся пути искусства и математики . Издательство Кембриджского университета. п. 10. ISBN  978-0-521-72876-8 .
  91. ^ Кинг, Джерри П. (1992). Искусство математики . Фосетт Колумбайн. стр. 8–9. ISBN  978-0-449-90835-8 .
  92. ^ Кинг, Джерри П. (1992). Искусство математики . Фосетт Колумбайн. стр. 135–139. ISBN  978-0-449-90835-8 .
  93. ^ Девлин, Кейт (2000). «У математиков разный мозг?» . Ген математики: как развивалось математическое мышление и почему числа похожи на сплетни . Основные книги. п. 140. ИСБН  978-0-465-01619-8 .
  94. ^ Василевская, Катажина (2012). «Математика в мире танца» (PDF) . Мосты . Проверено 1 сентября 2015 г.
  95. ^ Перейти обратно: а б Малькевич, Йозеф. «Математика и искусство» . Американское математическое общество . Проверено 1 сентября 2015 г.
  96. ^ Малькевич, Йозеф. «Математика и искусство. 2. Математические инструменты для художников» . Американское математическое общество . Проверено 1 сентября 2015 г.
  97. ^ «Математика и искусство: хорошее, плохое и красивое» . Математическая ассоциация Америки . Проверено 2 сентября 2015 г.
  98. ^ Коэн, Луиза (1 июля 2014 г.). «Как вращать цветовой круг, Тернер, Малевич и другие» . Галерея Тейт . Проверено 4 сентября 2015 г.
  99. ^ Кемп, Мартин (1992). Наука об искусстве: оптические темы в западном искусстве от Брунеллески до Сёра . Издательство Йельского университета. ISBN  978-968-867-185-6 .
  100. ^ Гейдж, Джон (1999). Цвет и культура: практика и значение от античности до абстракции . Издательство Калифорнийского университета. п. 207. ИСБН  978-0-520-22225-0 .
  101. ^ Малькевич, Йозеф. «Математика и искусство. 3. Симметрия» . Американское математическое общество . Проверено 1 сентября 2015 г.
  102. ^ Малькевич, Йозеф. «Математика и искусство. 4. Художники-математики и художники-математики» . Американское математическое общество . Проверено 1 сентября 2015 г.
  103. ^ Райт, Ричард (1988). «Некоторые проблемы развития компьютерного искусства как вида математического искусства». Леонардо . 1 (Электронное искусство, дополнительный выпуск): 103–110. дои : 10.2307/1557919 . JSTOR   1557919 .
  104. ^ Каладжиевский, Сашо (2008). Математика и искусство: введение в визуальную математику . Чепмен и Холл. ISBN  978-1-58488-913-7 .
  105. ^ Перейти обратно: а б Беддард, Хонор (26 мая 2011 г.). «Компьютерное искусство в музее Виктории и Альберта» . Музей Виктории и Альберта . Проверено 22 сентября 2015 г.
  106. ^ «Компьютер рисует: в каждом тысячи строк». Хранитель. 17 сентября 1962 г. , Беддард, 2015 г.
  107. ^ О'Ханрахан, Элейн (2005). Машины для рисования: машина создавала рисунки доктора Д. П. Генри, касающиеся концептуальных и технологических разработок в области машинного искусства (Великобритания, 1960–1968). Неопубликованный MPhil. Тезис . Университет Джона Мурса, Ливерпуль. в Беддарде, 2015 г.
  108. ^ Беллос, Алекс (24 февраля 2015 г.). «Улов дня: математик вылавливает странную и сложную рыбу» . Хранитель . Проверено 25 сентября 2015 г.
  109. ^ « Птица в полете (2016)» Хамида Надери Йегане . Американское математическое общество . 23 марта 2016 года . Проверено 6 апреля 2017 г.
  110. ^ Чанг, Стефи (18 сентября 2015 г.). «Следующий да Винчи? Математический гений, использующий формулы для создания фантастических произведений искусства» . CNN .
  111. ^ Левин, Голаны (2013). «Генеративные художники» . ЦМУЕМС . Проверено 27 октября 2015 г. Сюда входит ссылка на Hvidtfeldts Syntopia .
  112. ^ Веростко, Роман . «Алгористы» . Проверено 27 октября 2015 г.
  113. ^ Какер, Фелипе (2013). Многообразные зеркала: пересекающиеся пути искусства и математики . Издательство Кембриджского университета. стр. 315–317. ISBN  978-0-521-72876-8 .
  114. ^ Перейти обратно: а б Миллер, Артур И. (2001). Эйнштейн, Пикассо: Пространство, время и красота, вызывающая хаос . Нью-Йорк: Основные книги. п. 171 . ISBN  978-0-465-01860-4 .
  115. ^ Миллер, Артур И. (2012). Прозрение гения: образы и творчество в науке и искусстве . Спрингер. ISBN  978-1-4612-2388-7 .
  116. ^ Хендерсон, Линда Дэлримпл (1983). Четвертое измерение и неевклидова геометрия в современном искусстве . Издательство Принстонского университета.
  117. ^ Антлифф, Марк; Лейтен, Патрисия Ди (2001). Кубизм и культура (PDF) . Темза и Гудзон. Архивировано из оригинала (PDF) 26 июля 2020 года.
  118. ^ Эверделл, Уильям Р. (1997). Первые современники: профили истоков мысли двадцатого века . Издательство Чикагского университета. п. 312 . ISBN  978-0-226-22480-0 .
  119. ^ Грин, Кристофер (1987). Кубизм и его враги, современные движения и реакции во французском искусстве, 1916–1928 гг . Издательство Йельского университета. стр. 13–47.
  120. ^ Метцингер, Жан (октябрь – ноябрь 1910 г.). «Заметка о живописи». Сковорода : 60 ​​дюймов . Миллер (2001). Эйнштейн, Пикассо . Основные книги. п. 167 . ISBN  9780465018598 .
  121. ^ Метцингер, Жан (1972). Кубизм родился . Присутствие изданий. стр. 43–44. в Ферри, Люк (1993). Homo Aestheticus: изобретение вкуса в эпоху демократии Роберт Де Лоаиса, пер. Издательство Чикагского университета. п. 215 . ISBN  978-0-226-24459-4 .
  122. ^ «Уравнения Мана Рэя – человека. Путешествие от математики к Шекспиру. 7 февраля – 10 мая 2015 г.» . Коллекция Филлипса. 7 февраля 2015 года . Проверено 5 сентября 2015 г.
  123. ^ Адкок, Крейг (1987). «Эротизм Дюшана: математический анализ» . Интернет-исследования Айовы . 16 (1): 149–167. Архивировано из оригинала 7 сентября 2015 года.
  124. ^ Старейшина, Р. Брюс (2013). DADA, сюрреализм и кинематографический эффект . Издательство Университета Уилфрида Лорье. п. 602. ИСБН  978-1-55458-641-7 .
  125. ^ Таббс, Роберт (2014). Математика в литературе и искусстве ХХ века: содержание, форма, значение . Джу Пресс. п. 118. ИСБН  978-1-4214-1402-7 .
  126. ^ «Концептуальные формы и математические модели Хироши Сугимото, 7 февраля – 10 мая 2015 г.» . Коллекция Филлипса. 7 февраля 2015 года . Проверено 5 сентября 2015 г.
  127. ^ Таббс, Роберт (2014). Математика в литературе и искусстве ХХ века . Джонс Хопкинс. стр. 8–10. ISBN  978-1-4214-1380-8 .
  128. ^ Китс, Джонатон (13 февраля 2015 г.). «Посмотрите, как Ман Рэй сделал эллиптические параболоиды эротичными на выставке фотографий из коллекции Филлипса» . Форбс . Проверено 10 сентября 2015 г.
  129. ^ Гамвелл, Линн (2015). Математика и искусство: история культуры . Издательство Принстонского университета. стр. 311–312. ISBN  978-0-691-16528-8 .
  130. ^ Хеджеко, Джон, изд. (1968). «Генри Мур: Текст на его скульптуре». Генри Спенсер Мур . Саймон и Шустер. п. 105.
  131. ^ Перейти обратно: а б «Де Стиль» . Глоссарий Тейта . Тейт . Проверено 11 сентября 2015 г.
  132. ^ Керл, Джеймс Стивенс (2006). Словарь архитектуры и ландшафтной архитектуры (второе изд.). Издательство Оксфордского университета. ISBN  978-0-19-860678-9 .
  133. ^ Таббс, Роберт (2014). Математика в литературе и искусстве ХХ века: содержание, форма, значение . Джу Пресс. стр. 44–47. ISBN  978-1-4214-1402-7 .
  134. ^ «Гастроли: MC Эшер – Жизнь и творчество» . НГА. Архивировано из оригинала 3 августа 2009 года . Проверено 13 августа 2009 г.
  135. ^ «МС Эшер» . Mathacademy.com. 1 ноября 2007 года . Проверено 13 августа 2009 г.
  136. ^ Пенроуз, Л.С.; Пенроуз, Р. (1958). «Невозможные объекты: особый тип зрительной иллюзии». Британский журнал психологии . 49 (1): 31–33. дои : 10.1111/j.2044-8295.1958.tb00634.x . ПМИД   13536303 .
  137. ^ Кирусис, Лефтерис М.; Пападимитриу, Христос Х. (1985). «Сложность распознавания многогранных сцен». 26-й ежегодный симпозиум по основам информатики (SFCS, 1985) . стр. 175–185. CiteSeerX   10.1.1.100.4844 . дои : 10.1109/sfcs.1985.59 . ISBN  978-0-8186-0644-1 .
  138. ^ Купер, Мартин (2008). «Понятность интерпретации рисунков». Неравенство, поляризация и бедность . Спрингер-Верлаг. стр. 217–230 . дои : 10.1007/978-1-84800-229-6_9 . ISBN  978-1-84800-229-6 .
  139. ^ Робертс, Шивон (2006). « Кокстеринг с MC Эшером». Король бесконечного пространства: Дональд Коксетер, человек, который спас геометрию . Уокер. п. Глава 11.
  140. ^ Эшер, MC (1988). Мир MC Эшера . Случайный дом.
  141. ^ Эшер, MC; Вермюлен, МВт; Форд, К. (1989). Эшер об Эшере: исследуя бесконечность . Х.Н. Абрамс.
  142. ^ Малькевич, Йозеф. «Математика и ст. 5. Многогранники, разбиения и сечения» . Американское математическое общество . Проверено 1 сентября 2015 г.
  143. ^ Марколли, Матильда (июль 2016 г.). Понятие пространства в математике через призму современного искусства (PDF) . Книги века. стр. 23–26.
  144. ^ «Джон Робинсон» . Фонд Брэдшоу. 2007 . Проверено 13 августа 2009 г.
  145. ^ «Веб-сайт Геламана Фергюсона» . Helasculpt.com. Архивировано из оригинала 11 апреля 2009 года . Проверено 13 августа 2009 г.
  146. ^ Терстон, Уильям П. (1999). «Восьмеричный путь: математическая скульптура Геламана Фергюсона». В Леви, Сильвио (ред.). Том 35: Восьмеричный путь: красота кривой четвертого порядка Кляйна (PDF) . Публикации ИИГС. стр. 1–7.
  147. ^ «Рецензия на книгу MAA « Восьмеричный путь: красота кривой четвертого порядка Кляйна » . Маа.орг. 14 ноября 1993 года . Проверено 13 августа 2009 г.
  148. ^ «Путеводитель по праздничным подаркам для любителей математики» . Научный американец . 23 ноября 2014 года . Проверено 7 июня 2015 г.
  149. ^ Ханна, Рэйвен. «Галерея: Батшеба Гроссман» . Журнал «Симметрия» . Проверено 7 июня 2015 г.
  150. ^ Мастроянни, Брайан (26 мая 2015 г.). «Идеальное уравнение: художник сочетает математику и искусство» . Фокс Ньюс . Проверено 28 января 2021 г.
  151. ^ Флерон, Джулиан Ф.; Эке, Волкер; фон Ренессе, Кристина; Хочкисс, Филип К. (январь 2015 г.). Искусство и скульптура: математические исследования в области свободных искусств (2-е изд.). Проект «Открытие искусства математики».
  152. ^ Осинга, Хинке (2005). «Вязание крючком многообразия Лоренца» . Университет Окленда. Архивировано из оригинала 10 апреля 2015 года . Проверено 12 октября 2015 г.
  153. ^ Осинга, Хинке М .; Краускопф, Бернд (2004). «Вязание крючком многообразия Лоренца» . Математический интеллект . 26 (4): 25–37. CiteSeerX   10.1.1.108.4594 . дои : 10.1007/BF02985416 . S2CID   119728638 .
  154. ^ Дитц, Ада К. (1949). Алгебраические выражения в текстиле ручной работы (PDF) . Луисвилл, Кентукки: Маленький ткацкий станок. Архивировано из оригинала (PDF) 22 февраля 2016 г. Проверено 26 июня 2015 г.
  155. ^ Хендерсон, Дэвид; Таймина, Дайна (2001). «Вязание крючком гиперболической плоскости» (PDF) . Математический интеллект . 23 (2): 17–28. дои : 10.1007/BF03026623 . S2CID   120271314 . .
  156. ^ Барнетт, Ребекка (31 января 2017 г.). «Галерея: Что получится, если смешать математику, кораллы и вязание крючком? Это потрясающе» . Идеи.TED.com . Проверено 28 октября 2019 г.
  157. ^ Миллер, JCP (1970). «Периодические леса низкорослых деревьев». Философские труды Лондонского королевского общества . Серия А, Математические и физические науки. 266 (1172): 63–111. Бибкод : 1970РСПТА.266...63М . дои : 10.1098/rsta.1970.0003 . JSTOR   73779 . S2CID   123330469 .
  158. ^ «Пэт Эшфорт и Стив Пламмер - математики» . Шерстяные мысли . Проверено 4 октября 2015 г.
  159. ^ Уорд, Марк (20 августа 2012 г.). «Вязание заново: математика, феминизм и металл» . Новости BBC . Би-би-си . Проверено 23 сентября 2015 г.
  160. ^ Эшфорт, Пэт; Пламмер, Стив. «Губка Менгера» . Неясные мысли: в погоне за хитрой математикой . Проверено 23 сентября 2015 г.
  161. ^ Эшфорт, Пэт; Пламмер, Стив. «Афганцы для школ» . Неясные мысли: математика . Проверено 23 сентября 2015 г.
  162. ^ «Матганы с разницей» . Журнал «Просто вязание» . 1 июля 2008 г. Архивировано из оригинала 25 сентября 2015 г. Проверено 23 сентября 2015 г.
  163. ^ Жуффре, Дух (1903). Элементарный трактат по четырехмерной геометрии и введение в n-мерную геометрию (на французском языке). Париж: Готье-Виллар. OCLC   1445172 . Проверено 26 сентября 2015 г.
  164. ^ Секель, Элен (1994). «Антология ранних комментариев к Авиньонским девицам ». У Уильяма Рубина; Хелен Секель; Джудит Казинс (ред.). Авиньонские дамы . Нью-Йорк: Музей современного искусства. п. 264. ИСБН  978-0-87070-162-7 .
  165. ^ «Джотто ди Бондоне и помощники: триптих Стефанески» . Ватикан . Проверено 16 сентября 2015 г.
  166. ^ Гамвелл, Линн (2015). Математика и искусство: история культуры . Издательство Принстонского университета. стр. 337–338. ISBN  978-0-691-16528-8 .
  167. ^ Купер, Джонатан (5 сентября 2007 г.). «Искусство и математика» . Проверено 5 сентября 2015 г.
  168. ^ Хофштадтер, Дуглас Р. (1980). Гёдель, Эшер, Бах: Вечная золотая коса . Пингвин. п. 627. ИСБН  978-0-14-028920-6 .
  169. ^ Холл, Джеймс (10 июня 2011 г.). «Рене Магритт: Принцип удовольствия – выставка» . Хранитель . Проверено 5 сентября 2015 г.
  170. ^ Перейти обратно: а б Хофштадтер, Дуглас Р. (1980). Гёдель, Эшер, Бах: Вечная золотая коса . Пингвин. стр. 98–99, 690–717. ISBN  978-0-394-74502-2 .
  171. ^ Кинг, Эллиотт (2004). Адес, Дон (ред.). Дали . Милан: Бомпиани Арт. стр. 100-1 418–421.
  172. ^ «Балансировка камня» (PDF) . Ежемесячная математика (29). Июль 2013 . Проверено 10 июня 2017 г.
  173. ^ де Смит, Б. (2003). «Математическая структура гравюры Эшера». Уведомления Американского математического общества . 50 (4): 446–451.
  174. ^ Ленстра, Хендрик; Де Смит, Барт. «Применение математики к галерее печати Эшера» . Лейденский университет . Проверено 10 ноября 2015 г.
  175. ^ Станек, Бекка (16 июня 2014 г.). «Ван Гог и алгоритм: как математика может спасти искусство» . Журнал Тайм . Проверено 4 сентября 2015 г.
  176. ^ Сипикс, Мишель (18 мая 2009 г.). «Проект Ван Гога: искусство встречается с математикой в ​​продолжающихся международных исследованиях» . Общество промышленной и прикладной математики. Архивировано из оригинала 7 сентября 2015 года . Проверено 4 сентября 2015 г.
  177. ^ Эммерлинг, Леонард (2003). Джексон Поллок, 1912–1956 . Сумки. п. 63. ИСБН  978-3-8228-2132-9 .
  178. ^ Тейлор, Ричард П.; Миколич, Адам П.; Йонас, Дэвид (июнь 1999 г.). «Фрактальный анализ капельных картин Поллока» . Природа . 399 (6735): 422. Бибкод : 1999Natur.399..422T . дои : 10.1038/20833 . S2CID   204993516 .
  179. ^ Тейлор, Ричард; Миколич, Адам П.; Йонас, Дэвид (октябрь 1999 г.). «Фрактальный экспрессионизм: можно ли использовать науку для дальнейшего понимания искусства?» . Мир физики . 12 (10): 25–28. дои : 10.1088/2058-7058/12/10/21 . Архивировано из оригинала 5 августа 2012 г. Поллок умер в 1956 году, до того, как были открыты хаос и фракталы. Поэтому маловероятно, что Поллок сознательно понимал фракталы, которые рисовал. Тем не менее, его введение фракталов было намеренным. Например, цвет опорного слоя был выбран для создания максимально резкого контраста с фоном холста, и этот слой также занимает больше места на холсте, чем другие слои, что позволяет предположить, что Поллок хотел, чтобы этот высоко фрактальный опорный слой визуально доминировал над картиной. Более того, после того, как картины были закончены, он закреплял холст, чтобы удалить области возле края холста, где плотность рисунка была менее однородной.
  180. ^ Кинг, М. (2002). «От Макса Эрнста до Эрнста Маха: эпистемология в искусстве и науке» (PDF) . Проверено 17 сентября 2015 г.
  181. ^ Доджсон, Н.А. (2012). «Математическая характеристика полосатых картин Бриджит Райли» (PDF) . Журнал математики и искусств . 5 (2–3): 89–106. дои : 10.1080/17513472.2012.679468 . S2CID   10349985 . В течение начала 1980-х годов паттерны Райли перешли от более регулярных к более случайным (характеризуемым глобальной энтропией), не теряя при этом своей ритмической структуры (характеризуемой локальной энтропией). Это отражает описание Куделькой своего художественного развития.
  182. ^ Какер, Фелипе (2013). Многообразные зеркала: пересекающиеся пути искусства и математики . Издательство Кембриджского университета. стр. 116–120. ISBN  978-0-521-72876-8 .
  183. ^ Трейбергс, Андрейс (24 июля 2001 г.). «Геометрия перспективного рисунка на компьютере» . Университет Юты . Проверено 5 сентября 2015 г.
  184. ^ Гамвелл, Линн (2015). Математика и искусство: история культуры . Издательство Принстонского университета. п. XVIII. ISBN  978-0-691-16528-8 .
  185. ^ Малькевич, Йозеф. «Математика и искусство. 6. Оригами» . Американское математическое общество . Проверено 1 сентября 2015 г.
  186. ^ Рао, Т. Сундара (1893). Геометрические упражнения по складыванию бумаги . Эддисон.
  187. ^ Джастин, Дж. (июнь 1986 г.). «Математика оригами, часть 9». Британское оригами : 28–30. .
  188. ^ Альсина, Клауди; Нельсен, Роджер (2010). Очаровательные доказательства: путешествие в элегантную математику . Математические изложения Дольчиани. Том. 42. Математическая ассоциация Америки . п. 57. ИСБН  978-0-88385-348-1 .
  189. ^ Альперин, Роджер С .; Ланг, Роберт Дж. (2009). «Аксиомы одно-, двух- и многократного оригами» (PDF) . 4ОСМЕ .
  190. ^ Мир геометрических игрушек , Весна оригами , август 2007 г.
  191. ^ Какер, Фелипе (2013). Многообразные зеркала: пересекающиеся пути искусства и математики . Издательство Кембриджского университета. стр. 163–166. ISBN  978-0-521-72876-8 .
  192. ^ Гамвелл, Линн (2015). Математика и искусство: история культуры . Издательство Принстонского университета. стр. 406–410. ISBN  978-0-691-16528-8 .
  193. ^ Гика, Матила (2003). Геометрия искусства и жизни . Дувр. стр. ix – xi. ISBN  978-0-486-23542-4 .
  194. ^ Лоулор, Роберт (1982). Сакральная геометрия: философия и практика . Темза и Гудзон. ISBN  978-0-500-81030-9 .
  195. ^ Перейти обратно: а б Колтер, Пол (1998). «Небесные темы в искусстве и архитектуре» . Дартмутский колледж . Проверено 5 сентября 2015 г.
  196. ^ Мэддокс, Фиона (21 ноября 2014 г.). «10 лучших произведений Уильяма Блейка» . Хранитель . Проверено 25 декабря 2019 г.
  197. ^ «Уильям Блейк, Ньютон, 1795–1805» . Тейт . Октябрь 2018. Архивировано из оригинала 28 марта 2019 года.
  198. ^ Ливио, Марио (ноябрь 2002 г.). «Золотое сечение и эстетика» . Проверено 26 июня 2015 г.

Внешние ссылки [ править ]

Викискладе есть медиафайлы, связанные с математикой в ​​искусстве .
Retrieved from "https://en.wikipedia.org/w/index.php?title=Mathematics_and_art&oldid=1224731165"