Теория катастроф

В математике ; теория катастроф раздел теории бифуркаций при изучении динамических систем — это также частный частный случай более общей теории особенностей в геометрии .

Теория бифуркаций изучает и классифицирует явления, характеризующиеся внезапными изменениями в поведении, возникающими из-за небольших изменений обстоятельств, анализируя, как качественный характер решений уравнений зависит от параметров, входящих в уравнение. Это может привести к внезапным и драматическим изменениям, например, к непредсказуемому времени масштабу оползня и .

Теория катастроф возникла благодаря работам французского математика Рене Тома в 1960-х годах и стала очень популярной благодаря усилиям Кристофера Зеемана в 1970-х годах. Он рассматривает особый случай, когда долгосрочное устойчивое равновесие можно определить как минимум гладкой, четко определенной потенциальной функции ( функции Ляпунова ).Небольшие изменения некоторых параметров нелинейной системы могут привести к появлению или исчезновению равновесия или к смене притяжения на отталкивание и наоборот, что приводит к большим и внезапным изменениям поведения системы. Однако теория катастроф, рассматриваемая в более широком пространстве параметров , показывает, что такие точки бифуркации имеют тенденцию возникать как часть четко определенных качественных геометрических структур.

В конце 1970-х годов применение теории катастроф к областям, выходящим за рамки ее компетенции, начало подвергаться критике, особенно в биологии и социальных науках. ^[1]^[2] Залер и Суссманн в статье 1977 года в журнале Nature назвали такие приложения «характеризующимися неправильными рассуждениями, надуманными предположениями, ошибочными последствиями и преувеличенными утверждениями». ^[3] В результате теория катастроф стала менее популярной в приложениях. ^[4]

Элементарные катастрофы [ править ]

Теория катастроф анализирует вырожденные критические точки потенциальной функции — точки, в которых не только первая производная, но и одна или несколько высших производных потенциальной функции также равны нулю. Их называют ростками геометрий катастроф. Вырождение этих критических точек можно развернуть , разложив потенциальную функцию в ряд Тейлора по малым возмущениям параметров.

Когда вырожденные точки не просто случайны, но и структурно стабильны , они существуют как организующие центры для определенных геометрических структур меньшей вырожденности с критическими особенностями в пространстве параметров вокруг них. Если потенциальная функция зависит от двух или менее активных переменных и четырех или менее активных параметров, то существует только семь общих структур для этих бифуркационных геометрий с соответствующими стандартными формами, в которые ряд Тейлора вокруг ростков катастрофы может быть преобразован с помощью диффеоморфизма ( гладкое преобразование, обратное к которому также гладкое). ^{[ нужна ссылка ]} Теперь представлены эти семь основных типов с названиями, которые дал им Том.

Потенциальные функции одной активной переменной [ править ]

Теория катастроф изучает динамические системы, описывающие эволюцию. ^[5] переменной состояния $x$ через некоторое время $t$ :

{\dot {x}}={\dfrac {dx}{dt}}=-{\dfrac {dV(u,x)}{dx}}

В приведенном выше уравнении $V$ называется потенциальной функцией, а $u$ часто является вектором или скаляром, который параметризует потенциальную функцию. Стоимость $u$ может меняться со временем, и ее также можно назвать управляющей переменной. В следующих примерах такие параметры, как $a,b$ такие элементы управления.

катастрофа Складная

V=x^{3}+ax\,

При a < 0 потенциал V имеет два экстремума — один стабильный и один нестабильный. Если параметр a медленно увеличивать, система может следовать стабильной минимальной точке. Но при a = 0 устойчивый и нестабильный экстремумы встречаются и аннигилируют. Это точка бифуркации. При a > 0 устойчивого решения уже нет. Если проследить за физической системой через бифуркацию складки, можно обнаружить, что, когда a достигает 0, устойчивость решения a < 0 внезапно теряется, и система внезапно переходит к новому, совершенно иному поведению. Это бифуркационное значение параметра а иногда называют « переломным моментом ».

Куспидная катастрофа [ править ]

V=x^{4}+ax^{2}+bx\,

Геометрия возврата очень распространена, когда кто-то исследует, что происходит с бифуркацией складки, если второй параметр b в управляющее пространство добавляется . Варьируя параметры, можно обнаружить, что теперь существует кривая (синяя) из точек в пространстве ( a , b ), где стабильность теряется, где устойчивое решение внезапно переходит к альтернативному результату.

Но в геометрии возврата бифуркационная кривая зацикливается сама на себе, образуя вторую ветвь, в которой это альтернативное решение само теряет устойчивость и совершает прыжок обратно к исходному множеству решений. Таким образом, многократно увеличивая b , а затем уменьшая его, можно наблюдать петли гистерезиса , когда система поочередно следует одному решению, переходит к другому, следует за другим обратно, а затем возвращается к первому.

Однако это возможно только в области пространства параметров a < 0 . По мере увеличения a петли гистерезиса становятся все меньше и меньше, пока выше a = 0 они не исчезнут совсем (касповая катастрофа), и останется только одно устойчивое решение.

Можно также рассмотреть, что произойдет, если держать b постоянным и изменять a . В симметричном случае b = 0 наблюдается бифуркация в виде вил при уменьшении a , при этом одно устойчивое решение внезапно распадается на два устойчивых решения и одно неустойчивое решение, когда физическая система переходит к a < 0 через точку возврата (0,0). (пример спонтанного нарушения симметрии ). За пределами точки возврата не происходит резких изменений в физическом решении: при прохождении через кривую бифуркаций складок все, что происходит, — это становится доступным альтернативное второе решение.

Известное предположение состоит в том, что катастрофу куспида можно использовать для моделирования поведения собаки, находящейся в стрессе, которая может в ответ испугаться или разозлиться. ^[6] Предполагается, что при умеренном стрессе ( a > 0 ) у собаки будет плавный переход реакции от испуга к гневу, в зависимости от того, как ее спровоцировать. Но более высокие уровни напряжения соответствуют переходу в область ( a < 0 ). Затем, если собака начнет бояться, она будет оставаться запуганной, поскольку будет раздражаться все больше и больше, пока не достигнет точки «сгиба», когда она внезапно, прерывисто перейдет в режим гнева. Попав в «злой» режим, он останется злым, даже если параметр прямого раздражения значительно уменьшится.

Простая механическая система, «Машина катастроф Зеемана», прекрасно иллюстрирует катастрофу куспида. В этом устройстве плавные изменения положения конца пружины могут вызвать резкие изменения вращательного положения прикрепленного колеса. ^[7]

Катастрофический отказ сложной системы с параллельным резервированием можно оценить на основе соотношения между местными и внешними напряжениями. Модель механики структурного разрушения аналогична поведению касповой катастрофы. Модель прогнозирует резервную способность сложной системы.

Другие применения включают перенос электронов во внешнюю сферу, часто встречающийся в химических и биологических системах. ^[8] моделирование динамики облачных ядер конденсации в атмосфере, ^[9] и моделирование цен на недвижимость. ^[10]

Бифуркации складок и геометрия возврата — безусловно, наиболее важные практические следствия теории катастроф. Это закономерности, которые повторяются снова и снова в физике, технике и математическом моделировании.Они производят события сильного гравитационного линзирования и предоставляют астрономам один из методов, используемых для обнаружения черных дыр и темной материи Вселенной, посредством явления гравитационного линзирования, создающего множественные изображения далеких квазаров . ^[11]

Остальные простые геометрии катастроф по сравнению с ними очень специализированы и представлены здесь только ради любопытства.

Катастрофа «Махона хвоста» [ править ]

V=x^{5}+ax^{3}+bx^{2}+cx\,

Пространство параметров управления является трехмерным. Множество бифуркаций в пространстве параметров состоит из трех поверхностей бифуркаций складок, которые пересекаются в двух линиях бифуркаций возврата, которые, в свою очередь, встречаются в одной точке бифуркации ласточкиного хвоста.

При прохождении параметров через поверхность бифуркаций складок исчезают один минимум и один максимум потенциальной функции. В бифуркациях каспа два минимума и один максимум сменяются одним минимумом; за ними бифуркации складок исчезают. В точке «ласточкин хвост» два минимума и два максимума встречаются при одном значении x . Для значений a > 0 за пределами ласточкиного хвоста существует либо одна пара максимум-минимум, либо вообще нет, в зависимости от значений b и c . Таким образом , две поверхности бифуркаций складок и две линии бифуркаций возврата, где они встречаются при a < 0 , исчезают в точке «ласточкиного хвоста», и на их месте остается только одна поверхность бифуркаций складок. Сальвадора Дали Последняя картина «Ласточкин хвост » была основана на этой катастрофе.

Катастрофа бабочки [ править ]

V=x^{6}+ax^{4}+bx^{3}+cx^{2}+dx\,

В зависимости от значений параметров потенциальная функция может иметь три, два или один разный локальный минимум, разделенный точками бифуркаций складки. В точке бабочки различные 3-поверхности бифуркаций складок, 2-поверхности бифуркаций возврата и линии бифуркаций ласточкиного хвоста встречаются и исчезают, оставляя единственную структуру возврата, когда a > 0 .

двух активных Потенциальные функции переменных

Пупочные катастрофы являются примерами катастроф коранга 2. Их можно наблюдать в оптике на фокальных поверхностях, создаваемых светом, отражающимся от поверхности в трех измерениях, и они тесно связаны с геометрией почти сферических поверхностей: точка пупка .Том предположил, что катастрофа гиперболической пуповины моделирует разбиение волны, а эллиптическая пуповина моделирует создание волосоподобных структур.

пуповинная Гиперболическая катастрофа

V=x^{3}+y^{3}+axy+bx+cy\,

катастрофа Эллиптическая пуповинная

V={\frac {x^{3}}{3}}-xy^{2}+a(x^{2}+y^{2})+bx+cy\,

пуповинная Параболическая катастрофа

V=x^{2}y+y^{4}+ax^{2}+by^{2}78+cx+dy\,

Обозначения Арнольда [ править ]

Владимир Арнольд дал катастрофам классификацию ADE из-за глубокой связи с простыми группами Ли . ^{[ нужна ссылка ]}

А ₀ – неособая точка: $V=x$ .
А ₁ – локальный экстремум, либо устойчивый минимум, либо неустойчивый максимум. $V=\pm x^{2}+ax$ .
А ₂ - сгиб
А ₃ – куспид
А ₄ – ласточкин хвост
А ₅ – бабочка
A _k - представитель бесконечной последовательности форм одной переменной $V=x^{k+1}+\cdots$
Д ₄⁻ - эллиптическая пуповина
Д ₄⁺ - гиперболическая пуповина
D ₅ - параболический омбилик
D _k - представитель бесконечной последовательности дальнейших омбилических форм
Е ₆ – символическая пуповина $V=x^{3}+y^{4}+axy^{2}+bxy+cx+dy+ey^{2}$
E ₇
E₈

В теории особенностей есть объекты, соответствующие большинству других простых групп Ли.

Оптика [ править ]

Каустики под водой — это катастрофы, и их особые точки одни и те же, хотя поверхность воды постоянно меняется.

Край радуги представляет собой складчатую катастрофу, поэтому он имеет дифракционную картину, описываемую функцией Эйри. Это общий и стабильный параметр для любой формы капли воды.

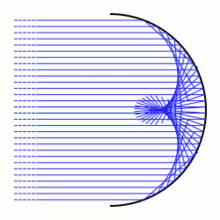
Как предсказывает теория катастроф, сингулярности являются общими и устойчивы при возмущениях. Это объясняет, почему яркие линии и поверхности устойчивы к возмущениям. Например, каустики , которые можно увидеть на дне бассейна, имеют характерную текстуру и имеют лишь несколько типов особых точек, хотя поверхность воды постоянно меняется. ^[12]

Край радуги , например, имеет складчатую катастрофу. Из-за волновой природы света катастрофа имеет мелкие дифракционные детали, описываемые функцией Эйри . Это общий результат, который не зависит от точной формы капли воды, поэтому край радуги всегда имеет форму функции Эйри. ^[13]^[14] Ту же катастрофу складки функции Эйри можно наблюдать и в ядерно-ядерном рассеянии («ядерная радуга»). ^[15]

Катастрофа куспида — следующая по простоте наблюдения. Из-за волновой природы света катастрофа имеет мелкие дифракционные детали, описываемые функцией Пирси . ^[16] Также наблюдались катастрофы более высокого порядка, такие как «парусник» и «бабочка». ^[17]

См. также [ править ]

Ссылки [ править ]

^ Мюррей, Стейси Р. «Взлет и падение теории катастроф» . Энциклопедия.com . Проверено 2 ноября 2021 г.
^ Хорган, Джон (2015). Конец науки: лицом к лицу с пределами знаний на закате научной эпохи . Нью-Йорк: Основные книги. п. 213. ИСБН 978-0-465-05085-7 .
^ Залер, Рафаэль С.; Суссманн, Гектор Дж. (1977). «Заявления и достижения прикладной теории катастроф» . Природа . 269 (5631): 759–763. Бибкод : 1977Natur.269..759Z . дои : 10.1038/269759a0 . ISSN 1476-4687 . S2CID 4205198 . Проверено 2 ноября 2021 г.
^ Россер, Дж. Баркли (октябрь 2007 г.). «Взлет и падение применения теории катастроф в экономике: ребенка выбросили вместе с водой?». Журнал экономической динамики и контроля . 31 (10): 3255–3280. дои : 10.1016/j.jedc.2006.09.013 .
^ Вагенмейкерс, Э.Дж.; ван дер Маас, HLJ; Моленаар, ПКМ (2005). «Подгонка к модели катастрофы» . Энциклопедия статистики в поведенческих науках .
^ EC Zeeman , Теория катастроф , Scientific American , апрель 1976 г.; стр. 65–70, 75–83.
^ Кросс, Дэниел Дж., Интерактивный рендеринг машины катастроф Зеемана.
^ Сюй, Ф (1990). «Применение теории катастроф к ∆G ^≠ Связь с -∆G в реакциях переноса электрона». Журнал физической химии . Новый эпизод. 166 : 79–91. doi : 10.1524/zpch.1990.166.Part_1.079 . S2CID 101078817 .
^ Арабас, С; Шима, С. (2017). «О нелинейностях (де)активации CCN» . Нелинейные процессы в геофизике . 24 (3): 535–542. arXiv : 1608.08187 . Бибкод : 2017NPGeo..24..535A . дои : 10.5194/npg-24-535-2017 . S2CID 24669360 .
^ Белей, Мирослав; Кулеша, Славомир (2012). «Моделирование цен на недвижимость в Ольштыне в условиях нестабильности» . Folia O Economica Stetinensia . 11 (1): 61–72. дои : 10.2478/v10031-012-0008-7 .
^ А.О. Петтерс, Х. Левин и Дж. Вамбсгансс, Теория сингулярности и гравитационное линзирование», Birkhäuser Boston (2001)
^ Берри, М.В.; Апстилл, К. (1980-01-01), Вольф, Э. (ред.), «IV Оптика катастроф: морфология каустиков и их дифракционные картины» , Progress in Optics , vol. 18, Elsevier, стр. 257–346 , получено 25 апреля 2024 г.
^ Адам, Джон А. (1 января 2002 г.). «Математическая физика радуг и славы» . Отчеты по физике . 356 (4): 229–365. дои : 10.1016/S0370-1573(01)00076-X . ISSN 0370-1573 .
^ «AMS :: Тематическая колонка :: Математика радуги, часть II» . Американское математическое общество . Проверено 25 апреля 2024 г.
^ Хоа, Дао Т; Эрцен, В. фон; Болен, Х.Г.; Окубо, С (01 марта 2007 г.). «Ядерное радужное рассеяние и ядерно-ядерный потенциал» . Журнал физики G: Ядерная физика и физика элементарных частиц . 34 (3): Р111–Р164. arXiv : nucl-th/0612100 . дои : 10.1088/0954-3899/34/3/R01 . ISSN 0954-3899 .
^ Макбит, Дэррил (ноябрь 2016 г.). Функция Пирси и катастрофа возврата (Диссертация).
^ Заннотти, Алессандро; Дибель, Фалько; Богуславский, Мартин; Денц, Корнелия (май 2017 г.). «Оптические катастрофы лучей типа «ласточкин хвост» и «бабочка» . Новый журнал физики . 19 (5): 053004. arXiv : 1703.07716 . дои : 10.1088/1367-2630/aa6ecd . ISSN 1367-2630 .

Библиография [ править ]

Арнольд, Владимир Игоревич (1992) Теория катастроф , 3-е изд. Берлин: Шпрингер-Верлаг
Афраймович В.С. , Арнольд В.И. и др. Теория бифуркаций и теория катастроф . ISBN 3-540-65379-1
Белей, М. Кулеша, С. (2013) «Моделирование цен на недвижимость в Ольштыне в условиях нестабильности», Folia O Economica Stetinensia 11 (1): 61–72, ISSN (онлайн) 1898–0198, ISSN (печать) 1730 –4237, два : 10.2478/v10031-012-0008-7
Кастриджано, Доменико П.Л. и Хейс, Сандра А. (2004) Теория катастроф , второе издание, Boulder: Westview ISBN 0-8133-4126-4
Гилмор, Роберт (1993) Теория катастроф для ученых и инженеров , Нью-Йорк: Дувр.
Петтерс, Арли О., Левин, Гарольд и Вамбсгансс, Иоахим (2001) Теория сингулярности и гравитационное линзирование , Бостон: Birkhäuser ISBN 0-8176-3668-4
Постл, Денис (1980) Теория катастроф - Прогнозируйте и избегайте личных катастроф , Фонтана в мягкой обложке ISBN 0-00-635559-5
Постон, Тим и Стюарт, Ян (1998) Катастрофа: теория и ее приложения , Нью-Йорк: Дувр. ISBN 0-486-69271-X
Саннс, Вернер (2000) Теория катастроф с Mathematica: геометрический подход , Германия: DAV
Сондерс, Питер Тимоти (1980) Введение в теорию катастроф , Кембридж, Англия: Издательство Кембриджского университета
Том, Рене (1989) Структурная стабильность и морфогенез: очерк общей теории моделей , Ридинг, Массачусетс: Аддисон-Уэсли ISBN 0-201-09419-3
Вудкок, Александр Эдвард Ричард и Дэвис, Монте. (1978) Теория катастроф , Нью-Йорк: EP Dutton ISBN 0-525-07812-6
Зееман, EC (1977) Избранные статьи по теории катастроф 1972–1977 , Ридинг, Массачусетс: Аддисон-Уэсли

Внешние ссылки [ править ]

[1] Мюррей, Стейси Р. «Взлет и падение теории катастроф» . Энциклопедия.com . Проверено 2 ноября 2021 г.

[2] Хорган, Джон (2015). Конец науки: лицом к лицу с пределами знаний на закате научной эпохи . Нью-Йорк: Основные книги. п. 213. ИСБН 978-0-465-05085-7 .

[3] Залер, Рафаэль С.; Суссманн, Гектор Дж. (1977). «Заявления и достижения прикладной теории катастроф» . Природа . 269 (5631): 759–763. Бибкод : 1977Natur.269..759Z . дои : 10.1038/269759a0 . ISSN 1476-4687 . S2CID 4205198 . Проверено 2 ноября 2021 г.

[4] Россер, Дж. Баркли (октябрь 2007 г.). «Взлет и падение применения теории катастроф в экономике: ребенка выбросили вместе с водой?». Журнал экономической динамики и контроля . 31 (10): 3255–3280. дои : 10.1016/j.jedc.2006.09.013 .

[5] Вагенмейкерс, Э.Дж.; ван дер Маас, HLJ; Моленаар, ПКМ (2005). «Подгонка к модели катастрофы» . Энциклопедия статистики в поведенческих науках .

[6] EC Zeeman , Теория катастроф , Scientific American , апрель 1976 г.; стр. 65–70, 75–83.

[7] Кросс, Дэниел Дж., Интерактивный рендеринг машины катастроф Зеемана.

[8] Сюй, Ф (1990). «Применение теории катастроф к ∆G ^≠ Связь с -∆G в реакциях переноса электрона». Журнал физической химии . Новый эпизод. 166 : 79–91. doi : 10.1524/zpch.1990.166.Part_1.079 . S2CID 101078817 .

[9] Арабас, С; Шима, С. (2017). «О нелинейностях (де)активации CCN» . Нелинейные процессы в геофизике . 24 (3): 535–542. arXiv : 1608.08187 . Бибкод : 2017NPGeo..24..535A . дои : 10.5194/npg-24-535-2017 . S2CID 24669360 .

[10] Белей, Мирослав; Кулеша, Славомир (2012). «Моделирование цен на недвижимость в Ольштыне в условиях нестабильности» . Folia O Economica Stetinensia . 11 (1): 61–72. дои : 10.2478/v10031-012-0008-7 .

[11] А.О. Петтерс, Х. Левин и Дж. Вамбсгансс, Теория сингулярности и гравитационное линзирование», Birkhäuser Boston (2001)

[12] Берри, М.В.; Апстилл, К. (1980-01-01), Вольф, Э. (ред.), «IV Оптика катастроф: морфология каустиков и их дифракционные картины» , Progress in Optics , vol. 18, Elsevier, стр. 257–346 , получено 25 апреля 2024 г.

[13] Адам, Джон А. (1 января 2002 г.). «Математическая физика радуг и славы» . Отчеты по физике . 356 (4): 229–365. дои : 10.1016/S0370-1573(01)00076-X . ISSN 0370-1573 .

[14] «AMS :: Тематическая колонка :: Математика радуги, часть II» . Американское математическое общество . Проверено 25 апреля 2024 г.

[15] Хоа, Дао Т; Эрцен, В. фон; Болен, Х.Г.; Окубо, С (01 марта 2007 г.). «Ядерное радужное рассеяние и ядерно-ядерный потенциал» . Журнал физики G: Ядерная физика и физика элементарных частиц . 34 (3): Р111–Р164. arXiv : nucl-th/0612100 . дои : 10.1088/0954-3899/34/3/R01 . ISSN 0954-3899 .

[16] Макбит, Дэррил (ноябрь 2016 г.). Функция Пирси и катастрофа возврата (Диссертация).

[17] Заннотти, Алессандро; Дибель, Фалько; Богуславский, Мартин; Денц, Корнелия (май 2017 г.). «Оптические катастрофы лучей типа «ласточкин хвост» и «бабочка» . Новый журнал физики . 19 (5): 053004. arXiv : 1703.07716 . дои : 10.1088/1367-2630/aa6ecd . ISSN 1367-2630 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]