Спонтанное нарушение симметрии
| Квантовая теория поля |
|---|
 |
| История |
| Статистическая механика |
|---|
 |
Спонтанное нарушение симметрии — это спонтанный процесс нарушения симметрии , при котором физическая система, находящаяся в симметричном состоянии, спонтанно переходит в асимметричное состояние. [1] [2] [3] В частности, он может описывать системы, в которых уравнения движения или лагранжиан с самой низкой энергией подчиняются симметрии, но вакуумные решения не обладают той же симметрией . Когда система переходит к одному из этих вакуумных решений, симметрия возмущений вокруг этого вакуума нарушается, хотя весь лагранжиан сохраняет эту симметрию.
Обзор [ править ]
По определению, спонтанное нарушение симметрии требует существования физических законов (например, квантовой механики ), которые инвариантны относительно преобразований симметрии (таких как сдвиг или вращение), так что любая пара результатов, отличающихся только этим преобразованием, имеет одинаковое распределение вероятностей. Например, если измерения наблюдаемой величины в любых двух разных положениях имеют одинаковое распределение вероятностей, наблюдаемая имеет трансляционную симметрию.
Спонтанное нарушение симметрии происходит, когда это соотношение нарушается, в то время как основные физические законы остаются симметричными.
И наоборот, при явном нарушении симметрии , если рассматриваются два результата, распределения вероятностей пары результатов могут быть разными. Например, в электрическом поле силы, действующие на заряженную частицу, различны в разных направлениях, поэтому вращательная симметрия явно нарушается электрическим полем, которое не обладает этой симметрией.
Фазы материи, такие как кристаллы, магниты и обычные сверхпроводники, а также простые фазовые переходы могут быть описаны спонтанным нарушением симметрии. Заметные исключения включают топологические фазы материи, такие как дробный квантовый эффект Холла .
Обычно, когда происходит спонтанное нарушение симметрии, наблюдаемые свойства системы изменяются множеством способов. Например, ожидается, что плотность, сжимаемость, коэффициент теплового расширения и удельная теплоемкость изменятся, когда жидкость станет твердой.
Примеры [ править ]
Потенциальная шляпа [ править ]
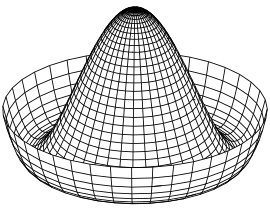
Рассмотрим симметричный направленный вверх купол с желобом, опоясывающим дно. Если шар поместить на самую вершину купола, система будет симметрична относительно вращения вокруг центральной оси. Но шар может спонтанно нарушить эту симметрию, скатившись по куполу во впадину, точку с наименьшей энергией. После этого мяч остановился в некоторой фиксированной точке по периметру. Купол и шар сохраняют свою индивидуальную симметрию, а система — нет. [4]
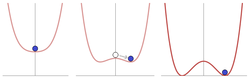
В простейшей идеализированной релятивистской модели спонтанно нарушенная симметрия суммируется с помощью наглядной скалярной теории поля . Соответствующий лагранжиан скалярного поля , который по сути определяет поведение системы, можно разделить на кинетические и потенциальные,
| ( 1 ) |
Именно в этом потенциальном сроке что происходит нарушение симметрии. Пример потенциала, предложенный Джеффри Голдстоуном. [5] показано на графике слева.
| . | ( 2 ) |
Этот потенциал имеет бесконечное количество возможных минимумов (состояний вакуума), определяемых формулой
| . | ( 3 ) |
для любого действительного θ между 0 и 2 π . Система также имеет неустойчивое вакуумное состояние, соответствующее Φ = 0 . Это состояние имеет симметрию U(1) . Однако как только система попадает в определенное стабильное состояние вакуума (что соответствует выбору θ ), эта симметрия оказывается потерянной или «спонтанно нарушенной».
Фактически, любой другой выбор θ будет иметь точно такую же энергию, и определяющие уравнения соблюдают симметрию, но основное состояние (вакуум) теории нарушает симметрию, подразумевая существование безмассового бозона Намбу – Голдстоуна , режима, работающего вокруг круга при минимуме этого потенциала и указывает на некоторую память об исходной симметрии в лагранжиане. [6] [7]
Другие примеры [ править ]
- Для ферромагнитных материалов основные законы инвариантны относительно пространственных вращений. Здесь параметром порядка является намагниченность , которая измеряет плотность магнитного диполя. Выше температуры Кюри параметр порядка равен нулю, что является пространственно инвариантным и нарушение симметрии отсутствует. Однако ниже температуры Кюри намагниченность приобретает постоянное неисчезающее значение, указывающее в определенном направлении (в идеализированной ситуации, когда мы имеем полное равновесие; в противном случае трансляционная симметрия также нарушается). Остаточные вращательные симметрии, которые оставляют ориентацию этого вектора неизменной, остаются неизменными, в отличие от других вращений, которые этого не делают и, таким образом, спонтанно нарушаются.
- Законы, описывающие твердое тело, инвариантны относительно полной евклидовой группы , но само твердое тело самопроизвольно разбивает эту группу на пространственную группу . Смещение и ориентация являются параметрами порядка.
- Общая теория относительности имеет симметрию Лоренца, но в космологических моделях FRW среднее поле 4-скоростей, определяемое усреднением скоростей галактик (галактики действуют как частицы газа в космологических масштабах), действует как параметр порядка, нарушающий эту симметрию. Аналогичные комментарии можно сделать и относительно космического микроволнового фона.
- Для электрослабой модели, как объяснялось ранее, компонент поля Хиггса обеспечивает параметр порядка, нарушающий электрослабую калибровочную симметрию на электромагнитную калибровочную симметрию. Как и в примере с ферромагнетиком, при электрослабой температуре происходит фазовый переход. Тот же комментарий о том, что мы не склонны замечать нарушения симметрии, позволяет понять, почему нам потребовалось так много времени, чтобы обнаружить электрослабое объединение.
- В сверхпроводниках существует коллективное поле конденсированного состояния ψ, которое действует как параметр порядка, нарушающий электромагнитную калибровочную симметрию.
- Возьмите тонкий цилиндрический пластиковый стержень и соедините оба конца вместе. До потери устойчивости система симметрична при вращении и поэтому явно цилиндрически симметрична. Но после коробления он выглядит иначе и асимметрично. Тем не менее, черты цилиндрической симметрии все же сохраняются: без учета трения не требуется никакой силы, чтобы свободно вращать стержень, смещая во времени основное состояние и представляющее собой колебание с исчезающей частотой, в отличие от радиальных колебаний в направлении пряжка. Эта мода вращения фактически является необходимым бозоном Намбу-Голдстоуна .
- Рассмотрим однородный слой жидкости в бесконечной горизонтальной плоскости. Эта система обладает всеми симметриями евклидовой плоскости. Но теперь равномерно нагрейте нижнюю поверхность так, чтобы она стала намного горячее верхней. Когда градиент температуры станет достаточно большим, конвекционные ячейки , нарушающие евклидову симметрию. образуются
- Рассмотрим бусину на круглом обруче, вращающемся вокруг вертикального диаметра . Поскольку скорость вращения постепенно увеличивается из состояния покоя, бусина первоначально будет оставаться в своей начальной точке равновесия в нижней части обруча (интуитивно стабильный, самый низкий гравитационный потенциал ). При определенной критической скорости вращения эта точка станет неустойчивой и бусинка перескочит в одно из двух других вновь созданных состояний равновесия, равноудаленных от центра. Первоначально система симметрична относительно диаметра, однако после прохождения критической скорости шарик оказывается в одной из двух новых точек равновесия, нарушая таким образом симметрию.
- Эксперимент с двумя баллонами является примером спонтанного нарушения симметрии, когда оба баллона первоначально надуваются до локального максимального давления. Когда некоторое количество воздуха перетекает из одного баллона в другой, давление в обоих баллонах падает, что делает систему более устойчивой в асимметричном состоянии.
В физике элементарных частиц [ править ]
В физике элементарных частиц частицы - носители силы обычно задаются уравнениями поля с калибровочной симметрией ; их уравнения предсказывают, что определенные измерения будут одинаковыми в любой точке поля. Например, уравнения поля могут предсказать, что масса двух кварков постоянна. Решение уравнений для определения массы каждого кварка может дать два решения. В одном решении кварк A тяжелее кварка B. Во втором решении кварк B тяжелее кварка A на ту же величину . Симметрия уравнений не отражается отдельными решениями, но отражается диапазоном решений.
Реальное измерение отражает только одно решение, представляющее собой нарушение симметрии базовой теории. «Скрытый» — лучший термин, чем «сломанный», потому что в этих уравнениях всегда присутствует симметрия. Это явление называется спонтанным нарушением симметрии (SSB), поскольку ничто (из того, что нам известно) не нарушает симметрию в уравнениях. [8] : 194–195 По природе спонтанного нарушения симметрии различные части ранней Вселенной нарушали симметрию в разных направлениях, что приводило к топологическим дефектам , таким как двумерные доменные границы , одномерные космические струны , нульмерные монополи и/или текстуры . в зависимости от соответствующей гомотопической группы и динамики теории. Например, нарушение симметрии Хиггса могло создать в качестве побочного продукта первичные космические струны. Гипотетическое Великого Объединения нарушение симметрии обычно приводит к образованию монополей , что создает трудности для Великого Объединения, если только монополи (вместе с любыми доменными стенками Великого Объединения) не будут изгнаны из нашей наблюдаемой Вселенной в результате космической инфляции . [9]
Киральная симметрия [ править ]
Нарушение киральной симметрии является примером спонтанного нарушения симметрии, влияющего на киральную симметрию сильных взаимодействий в физике элементарных частиц. Это свойство квантовой хромодинамики , квантовой теории поля, описывающей эти взаимодействия, и оно отвечает за большую часть массы (более 99%) нуклонов и , следовательно, всей обычной материи, поскольку оно превращает очень легкие связанные кварки в 100 раз более тяжелые составляющие барионов . Приближенными бозонами Намбу-Голдстоуна в этом процессе спонтанного нарушения симметрии являются пионы , масса которых на порядок легче массы нуклонов. Он послужил прототипом и важной составляющей механизма Хиггса, лежащего в основе нарушения электрослабой симметрии.
Механизм Хиггса [ править ]
Сильные, слабые и электромагнитные силы можно понимать как возникающие из калибровочной симметрии , что является избыточностью в описании симметрии. Механизм Хиггса , спонтанное нарушение калибровочной симметрии, является важным компонентом в понимании сверхпроводимости металлов и происхождения масс частиц в стандартной модели физики элементарных частиц. Термин «спонтанное нарушение симметрии» здесь используется неправильно, поскольку теорема Элицура утверждает, что локальные калибровочные симметрии никогда не могут быть спонтанно нарушены. Скорее, после фиксации калибровки глобальная симметрия (или избыточность) может быть нарушена способом, формально напоминающим спонтанное нарушение симметрии. Одним из важных последствий различия между истинными симметриями и калибровочными симметриями является то, что безмассовые моды Намбу – Голдстоуна, возникающие в результате спонтанного нарушения калибровочной симметрии, поглощаются описанием калибровочного векторного поля, обеспечивая массивные моды векторного поля, такие как плазменная мода в сверхпроводник или мода Хиггса, наблюдаемая в физике элементарных частиц.
В стандартной модели физики элементарных частиц спонтанное нарушение калибровочной симметрии SU(2) × U(1), связанное с электрослабым взаимодействием, порождает массы для нескольких частиц и разделяет электромагнитное и слабое взаимодействия. Бозоны W и Z являются элементарными частицами, которые опосредуют слабое взаимодействие , тогда как фотон опосредует электромагнитное взаимодействие . При энергиях, значительно превышающих 100 ГэВ, все эти частицы ведут себя схожим образом. Теория Вайнберга-Салама предсказывает, что при более низких энергиях эта симметрия нарушается, и возникают фотон и массивные W- и Z-бозоны. [10] Кроме того, фермионы последовательно наращивают массу.
Без спонтанного нарушения симметрии Стандартная модель взаимодействия элементарных частиц требует существования нескольких частиц. Однако тогда можно было бы предсказать, что некоторые частицы ( бозоны W и Z ) будут безмассовыми, хотя на самом деле они имеют массу. Чтобы преодолеть это, спонтанное нарушение симметрии дополняется механизмом Хиггса, чтобы придать этим частицам массу. Это также предполагает наличие новой частицы — бозона Хиггса , обнаруженной в 2012 году.
Сверхпроводимость металлов представляет собой аналог явления Хиггса в конденсированном состоянии, при котором конденсат куперовских пар электронов спонтанно нарушает калибровочную симметрию U (1), связанную со светом и электромагнетизмом.
симметрии динамической Нарушение
Динамическое нарушение симметрии (DSB) — это особая форма спонтанного нарушения симметрии, при которой основное состояние системы имеет пониженные свойства симметрии по сравнению с ее теоретическим описанием (т. е. лагранжианом ).
Динамическое нарушение глобальной симметрии — это спонтанное нарушение симметрии, которое происходит не на (классическом) уровне дерева (т. е. на уровне голого действия), а за счет квантовых поправок (т. е. на уровне эффективного действия ). .
Динамическое нарушение калибровочной симметрии более тонкое. При обычном спонтанном нарушении калибровочной симметрии в теории существует нестабильная частица Хиггса , которая переводит вакуум в фазу с нарушенной симметрией (т. е. электрослабые взаимодействия ). Однако при динамическом нарушении калибровочной симметрии в теории не действует ни одна нестабильная частица Хиггса. , но связанные состояния самой системы создают нестабильные поля, вызывающие фазовый переход. Например, Бардин, Хилл и Линднер опубликовали работу, в которой предпринимается попытка заменить обычный механизм Хиггса в стандартной модели DSB, который приводится в действие связанным состоянием топ-антитоп-кварков. (Такие модели, в которых составная частица играет роль бозона Хиггса, часто называют «составными моделями Хиггса».) [11] Динамическое нарушение калибровочной симметрии часто происходит из-за создания фермионного конденсата — например, кваркового конденсата , что связано с динамическим нарушением киральной симметрии в квантовой хромодинамике . Обычная сверхпроводимость является парадигмальным примером со стороны конденсированной среды, где фононное притяжение приводит к тому, что электроны связываются в пары, а затем конденсируются, тем самым нарушая электромагнитную калибровочную симметрию.
В физике конденсированного состояния [ править ]
Большинство фаз материи можно понять через призму спонтанного нарушения симметрии. Например, кристаллы представляют собой периодические массивы атомов, которые не инвариантны относительно всех трансляций (только при небольшом подмножестве трансляций вектора решетки). У магнитов есть северный и южный полюса, которые ориентированы в определенном направлении, нарушая вращательную симметрию . Помимо этих примеров, существует целый ряд других фаз материи, нарушающих симметрию, включая нематические фазы жидких кристаллов , волны зарядовой и спиновой плотности, сверхтекучие жидкости и многие другие.
Есть несколько известных примеров материи, которую нельзя описать спонтанным нарушением симметрии, в том числе: топологически упорядоченные фазы материи, такие как дробные квантовые холловские жидкости и спин-жидкости . Эти состояния не нарушают никакой симметрии, но представляют собой отдельные фазы материи. В отличие от случая спонтанного нарушения симметрии, не существует общей схемы описания таких состояний. [12]
Непрерывная симметрия [ править ]
Ферромагнетик — это каноническая система, которая спонтанно нарушает непрерывную симметрию спинов ниже температуры Кюри и при h = 0 , где h — внешнее магнитное поле. Ниже температуры Кюри энергия системы инвариантна относительно инверсии намагниченности m ( x ) такой, что m ( x ) = − m (− x ) . Симметрия спонтанно нарушается при h → 0 , когда гамильтониан становится инвариантным относительно инверсионного преобразования, но среднее значение не инвариантно.
Фазы вещества со спонтанным нарушением симметрии характеризуются параметром порядка, описывающим величину, нарушающую рассматриваемую симметрию. Например, в магните параметром порядка является локальная намагниченность.
Спонтанное нарушение непрерывной симметрии неизбежно сопровождается бесщелевыми (то есть эти моды не требуют затрат энергии на возбуждение) модами Намбу – Голдстоуна, связанными с медленными длинноволновыми флуктуациями параметра порядка. Например, колебательные моды в кристалле, известные как фононы, связаны с медленными флуктуациями плотности атомов кристалла. Соответствующая мода Голдстоуна для магнитов представляет собой колеблющиеся волны вращения, известные как спиновые волны. Для состояний, нарушающих симметрию, параметр порядка которых не является сохраняющейся величиной, моды Намбу – Голдстоуна обычно безмассовые и распространяются с постоянной скоростью.
Важная теорема Мермина и Вагнера утверждает, что при конечной температуре термически активированные флуктуации мод Намбу – Голдстоуна разрушают дальний порядок и предотвращают спонтанное нарушение симметрии в одно- и двумерных системах. Точно так же квантовые флуктуации параметра порядка предотвращают большинство типов непрерывного нарушения симметрии в одномерных системах даже при нулевой температуре. (Важным исключением являются ферромагнетики, параметр порядка которых, намагниченность, является точно сохраняющейся величиной и не имеет никаких квантовых флуктуаций.)
другие взаимодействующие системы на больших расстояниях, такие как цилиндрические изогнутые поверхности, взаимодействующие через кулоновский потенциал или потенциал Юкавы , нарушают трансляционную и вращательную симметрию. Было показано, что [13] Было показано, что при наличии симметричного гамильтониана и в пределе бесконечного объема система спонтанно принимает киральную конфигурацию, т. е. нарушает зеркальную плоскостную симметрию .
и Обобщение использование техническое
Чтобы произошло спонтанное нарушение симметрии, должна существовать система, в которой существует несколько равновероятных исходов. Таким образом, система в целом симметрична относительно этих результатов. Однако если система выбрана (т. е. если система фактически используется или каким-либо образом взаимодействует с ней), должен произойти конкретный результат. Хотя система в целом симметрична, она никогда не встречается с этой симметрией, а только в одном конкретном асимметричном состоянии. Следовательно, в этой теории говорят, что симметрия спонтанно нарушается. Тем не менее, тот факт, что каждый исход одинаково вероятен, является отражением лежащей в его основе симметрии, которую поэтому часто называют «скрытой симметрией», и имеет важные формальные последствия. (См. статью о бозоне Голдстоуна .)
Когда теория симметрична относительно группы симметрии , но требует, чтобы один элемент группы был различным, происходит спонтанное нарушение симметрии. Теория не должна диктовать, какой член является отдельным, а только то, что он является отдельным . С этого момента теорию можно рассматривать так, как будто этот элемент на самом деле различен, с оговоркой, что любые результаты, полученные таким способом, должны быть ресимметризированы, принимая среднее значение каждого из элементов группы как отдельное.
Важнейшим понятием в физических теориях является параметр порядка . Если существует поле (часто фоновое поле), которое приобретает математическое ожидание (не обязательно вакуумное математическое ожидание ), которое не является инвариантным относительно рассматриваемой симметрии, мы говорим, что система находится в упорядоченной фазе , а симметрия спонтанно возникает. сломанный. Это связано с тем, что другие подсистемы взаимодействуют с параметром порядка, который определяет «систему отсчета», относительно которой следует измерять. В этом случае вакуумное состояние не подчиняется начальной симметрии (которая сохраняла бы его инвариантной в линейно реализуемой вигнеровской моде, в которой оно было бы синглетным), а вместо этого изменяется под действием (скрытой) симметрии, реализованной теперь в (нелинейный) Режим Намбу–Голдстоуна . Обычно в отсутствие механизма Хиггса безмассовые голдстоуновские бозоны возникают .
Группа симметрии может быть дискретной, как, например, пространственная группа кристалла, или непрерывной (например, группа Ли ), как, например, вращательная симметрия пространства. Однако если система содержит только одно пространственное измерение, то в вакуумном состоянии полной квантовой теории могут быть нарушены только дискретные симметрии , хотя классическое решение может нарушить непрерывную симметрию.
Нобелевская премия [ править ]
7 октября 2008 года Шведская королевская академия наук присудила Нобелевскую премию по физике 2008 года трем учёным за работу по нарушению симметрии в субатомной физике. Йоитиро Намбу из Чикагского университета получил половину премии за открытие механизма спонтанного нарушения симметрии в контексте сильных взаимодействий, в частности нарушения киральной симметрии . Физики Макото Кобаяси и Тошихидэ Маскава из Киотского университета разделили вторую половину премии за открытие причины явного нарушения CP-симметрии в слабых взаимодействиях. [14] Это происхождение в конечном итоге зависит от механизма Хиггса, но до сих пор понимается как «просто так» особенность связей Хиггса, а не как явление спонтанного нарушения симметрии.
См. также [ править ]
- Автокаталитические реакции и создание порядка
- Теория катастроф
- Нарушение киральной симметрии
- CP-нарушение
- Шар Ферми
- Калибровочная теория гравитации
- Голдстоун бозон
- Теория Великого объединения
- Механизм Хиггса
- Бозон Хиггса
- Поле Хиггса (классическое)
- Необратимость
- Магнитный катализ нарушения киральной симметрии
- Теорема Мермина – Вагнера
- Купол Нортона
- Фазовый переход второго рода
- Спонтанный абсолютный асимметричный синтез в химии
- Нарушение симметрии
- Тахионная конденсация
- Статьи о нарушении симметрии PRL 1964 г.
Примечания [ править ]
- ^ Обратите внимание, что (как и в случае фундаментального спонтанного нарушения калибровочной симметрии, вызванного Хиггсом) термин «нарушение симметрии» является неправильным применительно к калибровочным симметриям.
Ссылки [ править ]
- ^ Миранский, Владимир А. (1993). Динамическое нарушение симметрии в квантовых теориях поля . Всемирная научная. п. 15. ISBN 9810215584 .
- ^ Ародз, Хенрик; Дзиармага, Яцек; Журек, Войцех Хуберт, ред. Паттерны нарушения симметрии . Спрингер. стр. 141. ISBN 9781402017452 .
- ^ Корнелл, Джеймс, изд. (21 ноября 1991 г.). Пузыри, пустоты и неровности во времени: Новая космология . Издательство Кембриджского университета. п. 125. ИСБН 9780521426732 .
- ^ Эдельман, Джеральд М. (1992). Яркий воздух, яркий огонь: о делах разума . Нью-Йорк: BasicBooks. п. 203 .
- ^ Голдстоун, Дж. (1961). «Теории поля с «сверхпроводниковыми» решениями» . Иль Нуово Чименто . 19 (1): 154–164. Бибкод : 1961NCim...19..154G . дои : 10.1007/BF02812722 . S2CID 120409034 .
- ^ Муньос-Вега, Р.; Гарсиа-Кирос, А.; Лопес-Чавес, Эрнесто; Салинас-Эрнандес, Энкарнасьон (2012). «Спонтанное нарушение симметрии в нерелятивистской квантовой механике». Американский журнал физики . 80 (10): 891–897. arXiv : 1205.4773 . Бибкод : 2012AmJPh..80..891M . дои : 10.1119/1.4739927 . S2CID 119131875 .
- ^ Киббл, Т.В. Б. (2015). «История нарушения электрослабой симметрии» . Физический журнал: серия конференций . 626 (1): 012001. arXiv : 1502.06276 . Бибкод : 2015JPhCS.626a2001K . дои : 10.1088/1742-6596/626/1/012001 . S2CID 119290021 .
- ^ Стивен Вайнберг (20 апреля 2011 г.). Мечты об окончательной теории: поиск учеными окончательных законов природы . Издательская группа Кнопфа Doubleday. ISBN 978-0-307-78786-6 .
- ^ Жаннеро, Рэйчел; Роше, Джонатан; Сакеллариаду, Майри (24 ноября 2003 г.). «Насколько общим является формирование космических струн в суперсимметричных теориях Великого объединения». Физический обзор D . 68 (10): 103514. arXiv : hep-ph/0308134 . Бибкод : 2003PhRvD..68j3514J . дои : 10.1103/PhysRevD.68.103514 .
- ^ Краткая история времени, Стивен Хокинг, Бантам; Юбилейное издание, 10 лет (1998 г.). стр. 73–74. [ ISBN отсутствует ]
- ^ Уильям А. Бардин ; Кристофер Т. Хилл ; Манфред Линднер (1990). «Минимальное нарушение динамической симметрии стандартной модели». Физический обзор D . 41 (5): 1647–1660. Бибкод : 1990PhRvD..41.1647B . дои : 10.1103/PhysRevD.41.1647 . ПМИД 10012522 .
- ^ Чен, Се; Гу, Чжэн-Чэн; Вэнь, Сяо-Ган (2010). «Локальное унитарное преобразование, дальнодействующая квантовая запутанность, перенормировка волновой функции и топологический порядок». Физ. Преподобный Б. 82 (15): 155138. arXiv : 1004.3835 . Бибкод : 2010PhRvB..82o5138C . дои : 10.1103/physrevb.82.155138 . S2CID 14593420 .
- ^ Кольстедт, КЛ; Верницци, Г.; Солис, Ф.Дж.; Ольвера де ла Крус, М. (2007). «Спонтанная хиральность посредством электростатических сил дальнего действия». Письма о физических отзывах . 99 (3): 030602. arXiv : 0704.3435 . Бибкод : 2007PhRvL..99c0602K . doi : 10.1103/PhysRevLett.99.030602 . ПМИД 17678276 . S2CID 37983980 .
- ^ Нобелевский фонд. «Нобелевская премия по физике 2008» . nobelprize.org . Проверено 15 января 2008 г.
Внешние ссылки [ править ]
- Педагогическое введение в нарушение электрослабой симметрии с пошаговыми выводами многих ключевых отношений, не встречающимися в текстах, см. на http://www.quantumfieldtheory.info/Electroweak_Sym_breaking.pdf.
- Спонтанное нарушение симметрии
- Письма о физических обзорах - документы, посвященные 50-летнему юбилею
- В CERN Courier Стивен Вайнберг размышляет о спонтанном нарушении симметрии.
- Механизм Энглерта – Браута – Хиггса – Гуральника – Хагена – Киббла в Scholarpedia
- История механизма Энглерта – Браута – Хиггса – Гуральника – Хагена – Киббла в Scholarpedia
- История развития Гуральником, Хагеном и Кибблом теории спонтанного нарушения симметрии и калибровочных частиц
- Международный журнал современной физики A: История развития Гуральником, Хагеном и Кибблом теории спонтанного нарушения симметрии и калибровочных частиц
- Гуральник Г.С.; Хаген, Ч.Р. и Киббл, TWB (1967). Нарушенные симметрии и теорема Голдстоуна. Достижения физики, вып. 2 Издательство Interscience, Нью-Йорк. стр. 567–708. ISBN 0-470-17057-3
- Спонтанное нарушение симметрии в калибровочных теориях: исторический обзор
- Издательство Королевского общества: Спонтанное нарушение симметрии в калибровочных теориях
- Кембриджский университет, Дэвид Тонг: Лекции по квантовой теории поля для студентов магистратуры.





