Микроканонический ансамбль

В статистической механике микроканонический ансамбль — это статистический ансамбль , который представляет возможные состояния механической системы, полная энергия которой точно задана. Предполагается, что система изолирована в том смысле, что она не может обмениваться энергией или частицами с окружающей средой, так что (за счет сохранения энергии ) энергия системы не меняется со временем.

Основными макроскопическими переменными микроканонического ансамбля являются общее количество частиц в системе (символ: N ), объем системы (символ: V ), а также полная энергия в системе (символ: E ). Каждый из них предполагается постоянным в ансамбле. По этой причине микроканонический ансамбль иногда называют NVE ансамблем .

Проще говоря, микроканонический ансамбль определяется путем присвоения равной вероятности каждому микросостоянию , энергия которого попадает в диапазон с центром в E . Всем остальным микросостояниям присваивается вероятность, равная нулю. Поскольку сумма вероятностей должна составлять 1, вероятность P является обратной величиной числа микросостояний W в диапазоне энергий:

$P=1/W,$

Затем ширина диапазона энергии уменьшается до тех пор, пока он не станет узким , по-прежнему с центром в точке E. бесконечно В пределе этого процесса получается микроканонический ансамбль.

Применимость

Из-за своей связи с элементарными предположениями равновесной статистической механики (особенно с постулатом априорного равенства вероятностей ) микроканонический ансамбль является важным концептуальным строительным блоком теории. Иногда его считают фундаментальным распределением равновесной статистической механики. Это также полезно в некоторых численных приложениях, таких как молекулярная динамика . С другой стороны, большинство нетривиальных систем математически громоздки для описания в микроканоническом ансамбле, а также существуют неясности в отношении определений энтропии и температуры. По этим причинам для теоретических расчетов часто отдают предпочтение другим ансамблям.

Применимость микроканонического ансамбля к реальным системам зависит от важности энергетических флуктуаций, которые могут возникнуть в результате взаимодействия между системой и ее окружением, а также неконтролируемых факторов при подготовке системы. Как правило, флуктуации незначительны, если система макроскопически велика или если она изготовлена ​​с точно известной энергией и после этого поддерживается почти изолированной от окружающей среды. В таких случаях применим микроканонический ансамбль. В противном случае более подходящими являются разные ансамбли, например канонический ансамбль (флуктуирующая энергия) или большой канонический ансамбль (флуктуирующая энергия и число частиц).

Свойства

Термодинамические величины

Фундаментальным термодинамическим потенциалом микроканонического ансамбля является энтропия . Существует как минимум три возможных определения, каждое из которых дается в терминах функции фазового объема v ( E ) , которая подсчитывает общее количество состояний с энергией меньше E ( Точные выражения см. в разделе « математическое определение v » ):

• Больцмана энтропия

  $S_{\text{B}}=k\log W=k\log \left(\omega {\frac {dv}{dE}}\right),$

• «объемная энтропия»
  $S_{v}=k\log v,$
• «поверхностная энтропия»
  $S_{s}=k\log {\frac {dv}{dE}}=S_{\text{B}}-k\log \omega .$

В микроканоническом ансамбле температура является производной величиной, а не внешним управляющим параметром. Он определяется как производная выбранной энтропии по энергии. Например, «температуры» T _v и T _s можно определить следующим образом:

$1/T_{v}=dS_{v}/dE,$

$1/T_{s}=dS_{s}/dE=dS_{\text{B}}/dE.$

Как и в случае с энтропией, существует множество способов понять температуру в микроканоническом ансамбле. В более общем плане соответствие между этими определениями, основанными на ансамблях, и их термодинамическими аналогами не является идеальным, особенно для конечных систем.

Микроканоническое давление и химический потенциал определяются выражением:

${\frac {p}{T}}={\frac {\partial S}{\partial V}};\qquad {\frac {\mu }{T}}=-{\frac {\partial S}{\partial N}}$

Фазовые переходы

Согласно строгому определению, фазовые переходы соответствуют неаналитическому поведению термодинамического потенциала или его производных. Согласно этому определению, фазовые переходы в микроканоническом ансамбле могут происходить в системах любого размера. Это контрастирует с каноническими и большими каноническими ансамблями, для которых фазовые переходы могут происходить только в термодинамическом пределе , т. е. в системах с бесконечным числом степеней свободы. Грубо говоря, резервуары, определяющие канонические или большие канонические ансамбли, вносят флуктуации, которые «сглаживают» любое неаналитическое поведение свободной энергии конечных систем. Этот эффект сглаживания обычно незначителен в макроскопических системах, которые достаточно велики, чтобы свободная энергия могла очень хорошо аппроксимировать неаналитическое поведение. Однако техническая разница в ансамблях может быть важна при теоретическом анализе небольших систем.

энтропия

Для данной механической системы (фиксированных N , V ) и данного диапазона энергий равномерное распределение вероятности P по микросостояниям (как в микроканоническом ансамбле) максимизирует среднее значение по ансамблю −⟨log P ⟩ .

аналогии

в статистической механике Ранние работы Людвига Больцмана привели к его одноименному уравнению энтропии для системы с заданной полной энергией S = k log W , где W — количество различных состояний, доступных системе при этой энергии. Больцман не вдавался в подробности того, что именно представляет собой совокупность различных состояний системы, за исключением частного случая идеального газа. Эту тему до конца исследовал Джозайя Уиллард Гиббс , который разработал обобщенную статистическую механику для произвольных механических систем и определил микроканонический ансамбль, описанный в этой статье. Гиббс тщательно исследовал аналогии между микроканоническим ансамблем и термодинамикой, особенно то, как они нарушаются в случае систем с малым числом степеней свободы. Он ввел еще два определения микроканонической энтропии, не зависящие от ω, — описанную выше объемную и поверхностную энтропию. (Обратите внимание, что поверхностная энтропия отличается от энтропии Больцмана только смещением, зависящим от ω .)

Объемная энтропия S _v и связанная с ней T _v образуют близкую аналогию с термодинамической энтропией и температурой. Можно показать именно это

$dE=T_{\rm {v}}dS_{\rm {v}}-\langle P\rangle dV,$

( ⟨ P ⟩ — среднее давление по ансамблю), как и ожидалось для первого закона термодинамики . Аналогичное уравнение можно найти для поверхностной (больцмановской) энтропии и связанной с ней T _s , однако «давление» в этом уравнении представляет собой сложную величину, не связанную со средним давлением.

Микроканонические T _v и T _s не совсем удовлетворительны по своей аналогии с температурой. За пределами термодинамического предела возникает ряд артефактов.

• Нетривиальный результат объединения двух систем : две системы, каждая из которых описывается независимым микроканоническим ансамблем, можно привести в тепловой контакт и позволить им прийти в равновесие в объединенную систему, также описываемую микроканоническим ансамблем. К сожалению, поток энергии между двумя системами не может быть предсказан на основе начальных T. значений Даже если начальные значения T равны, возможна передача энергии. Более того, Т комбинации отличается от исходных значений. Это противоречит интуитивному представлению о том, что температура должна быть интенсивной величиной и что две системы с одинаковой температурой не должны подвергаться воздействию теплового контакта.
• Странное поведение для систем с несколькими частицами : многие результаты, такие как микроканоническая теорема о равнораспределении, приобретают смещение на одну или две степени свободы, когда они записаны в терминах T _s . Для небольших систем это смещение существенно, и поэтому, если мы сделаем S _{аналогом энтропии} , необходимо сделать несколько исключений для систем только с одной или двумя степенями свободы.
• Ложные отрицательные температуры : Отрицательное T _s возникает всякий раз, когда плотность состояний уменьшается с энергией. В некоторых системах плотность состояний не монотонна по энергии, поэтому T _s может менять знак несколько раз с увеличением энергии.

Предпочтительным решением этих проблем является отказ от использования микроканонического ансамбля. Во многих реальных случаях система термостатируется в термостате, так что энергия точно неизвестна. Тогда более точным описанием является канонический ансамбль или большой канонический ансамбль , оба из которых полностью соответствуют термодинамике.

Точные выражения для ансамбля

Точное математическое выражение статистического ансамбля зависит от типа рассматриваемой механики — квантовой или классической — поскольку понятие «микросостояния» в этих двух случаях существенно различается. В квантовой механике диагонализация обеспечивает дискретный набор микросостояний с определенными энергиями. Классический механический случай вместо этого включает интеграл по каноническому фазовому пространству , и размер микросостояний в фазовом пространстве может быть выбран несколько произвольно.

Для построения микроканонического ансамбля в обоих видах механики необходимо сначала указать диапазон энергий. В выражениях ниже функции $f\left({\tfrac {H-E}{\omega }}\right)$ (функция H с максимумом в точке E с шириной ω ) будет использоваться для представления диапазона энергий, в который можно включать состояния. Примером этой функции может быть

$f(x)={\begin{cases}1,&\mathrm {if} ~|x|<{\tfrac {1}{2}},\\0,&\mathrm {otherwise.} \end{cases}}$

или, более гладко,

$f(x)=e^{-\pi x^{2}}.$

Квантово-механический

Пример микроканонического ансамбля квантовой системы, состоящей из одной частицы в потенциальной яме.

График всех возможных состояний этой системы. Доступные стационарные состояния отображаются в виде горизонтальных полос разной темноты в соответствии с | ψ _я (х)| ² .

Ансамбль, содержащий только те состояния, которые находятся в узком интервале энергий. При обращении энергетической ширины к нулю получается микроканонический ансамбль (при условии, что интервал содержит хотя бы одно состояние).

Гамильтониан частицы имеет тип Шрёдингера , Ĥ = U ( x ) + p ² /2 м (потенциал U ( x ) показан красной кривой). На каждой панели показан график положения энергии с различными стационарными состояниями, а также боковой график, показывающий распределение состояний по энергии.

Дополнительная информация о представлении ансамблей в квантовой механике: Статистический ансамбль (математическая физика).

Статистический ансамбль в квантовой механике представляется матрицей плотности , обозначаемой ${\hat {\rho }}$. Микроканонический ансамбль можно записать с использованием обозначений брекета в терминах собственных состояний энергии и собственных значений энергии. Учитывая полную основу собственных состояний энергии | ψ _i ⟩ , индексированный i , микроканонический ансамбль

${\hat {\rho }}={\frac {1}{W}}\sum _{i}f\left({\tfrac {H_{i}-E}{\omega }}\right)|\psi _{i}\rangle \langle \psi _{i}|,$

где H _i — собственные значения энергии, определяемые формулой ${\hat {H}}|\psi _{i}\rangle =H_{i}|\psi _{i}\rangle$ (здесь Ĥ — оператор полной энергии системы, т. е. оператор Гамильтона ). Значение W определяется требованием, чтобы ${\hat {\rho }}$ является нормализованной матрицей плотности, и поэтому

$W=\sum _{i}f\left({\tfrac {H_{i}-E}{\omega }}\right).$

Функция объема состояния (используемая для расчета энтропии) имеет вид

$v(E)=\sum _{H_{i}<E}1.$

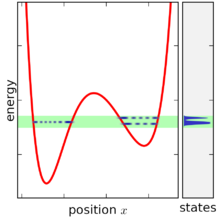
Микроканонический ансамбль определяется путем принятия предела матрицы плотности, когда энергетическая ширина стремится к нулю, однако проблематическая ситуация возникает, когда энергетическая ширина становится меньше расстояния между энергетическими уровнями. При очень малой энергетической ширине ансамбль вообще не существует для большинства значений E , поскольку ни одно состояние не попадает в этот диапазон. Когда ансамбль действительно существует, он обычно содержит только одно ( или два ) состояния, поскольку в сложной системе уровни энергии становятся равными только случайно ( см. В теории случайных матриц более подробное обсуждение этого вопроса ). Более того, функция объема состояния также увеличивается только с дискретными приращениями, поэтому ее производная всегда бесконечна или равна нулю, что затрудняет определение плотности состояний. Эту проблему можно решить, если не приводить диапазон энергий полностью к нулю и сглаживать функцию объема состояния, однако это усложняет определение ансамбля, поскольку тогда возникает необходимость указывать диапазон энергий в дополнение к другим переменным (вместе , ансамбль NVEω ).

Классическая механика

Пример микроканонического ансамбля классической системы, состоящей из одной частицы в потенциальной яме.

График всех возможных состояний этой системы. Доступные физические состояния равномерно распределены в фазовом пространстве, но с неравномерным распределением по энергии; боковой график отображает dv / dE .

Ансамбль, ограниченный только теми состояниями, которые находятся в узком интервале энергий. Этот ансамбль выглядит как тонкая оболочка в фазовом пространстве. При обращении энергетической ширины к нулю получается микроканонический ансамбль.

На каждой панели показано фазовое пространство (верхний график) и пространство энергетических позиций (нижний график). Гамильтониан частицы H = U ( x ) + p ² /2 м , потенциал U ( x ) показан красной кривой. На боковом графике показано распределение состояний по энергии.

Дополнительная информация о представлении ансамблей в классической механике: Статистический ансамбль (математическая физика).

В классической механике ансамбль представлен совместной функцией плотности вероятности ρ ( p ₁ , … p _n , q ₁ , … q _n ), системы определенной в фазовом пространстве . Фазовое пространство имеет n обобщенных координат, называемых q ₁ , … q _n , и n связанных с ними канонических импульсов, называемых p ₁ , … p _n .

Функция плотности вероятности для микроканонического ансамбля:

$\rho ={\frac {1}{h^{n}C}}{\frac {1}{W}}f\left({\tfrac {H-E}{\omega }}\right),$

где

• H — полная энергия ( гамильтониан ) системы, функция фазы ( p ₁ , … q _n ) ,
• h — произвольная, но заранее определенная константа с единицами энергии×время , определяющая размер одного микросостояния и обеспечивающая правильные размеры ρ .
• C — поправочный коэффициент завышения, часто используемый для систем частиц, в которых идентичные частицы могут меняться местами друг с другом.

Опять же, значение W определяется требованием, чтобы ρ была нормализованной функцией плотности вероятности:

$W=\int \ldots \int {\frac {1}{h^{n}C}}f\left({\tfrac {H-E}{\omega }}\right)\,dp_{1}\ldots dq_{n}$

Этот интеграл берется по всему фазовому пространству . Функция объема состояния (используемая для расчета энтропии) определяется формулой

$v(E)=\int \ldots \int _{H<E}{\frac {1}{h^{n}C}}\,dp_{1}\ldots dq_{n}.$

Поскольку энергетическая ширина ω принимается равной нулю, значение W уменьшается пропорционально ω как W = ω ( dv / dE ) .

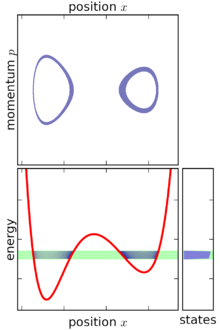
Основываясь на приведенном выше определении, микроканонический ансамбль можно представить как бесконечно тонкую оболочку в фазовом пространстве с центром на поверхности с постоянной энергией. Хотя микроканонический ансамбль ограничен этой поверхностью, он не обязательно равномерно распределен по этой поверхности: если градиент энергии в фазовом пространстве меняется, то микроканонический ансамбль «толще» (более концентрирован) в одних частях поверхности, чем в других. . Эта особенность является неизбежным следствием требования, чтобы микроканонический ансамбль был стационарным.

Примеры

Идеальный газ

Фундаментальной величиной в микроканоническом ансамбле является $W(E,V,N)$, который равен объему фазового пространства, совместимому с заданными $(E,V,N)$. От $W$, все термодинамические величины могут быть вычислены. Для идеального газа энергия не зависит от положения частиц, которые, следовательно, вносят вклад в $V^{N}$ к $W$. Импульсы, напротив, ограничены $3N$-мерная (гипер-)сферическая оболочка радиуса ${\sqrt {2mE}}$; их вклад равен поверхностному объему этой оболочки. Полученное выражение для $W$ является:

$W={\frac {V^{N}}{N!}}{\frac {2\pi ^{3N/2}}{\Gamma (3N/2)}}\left(2mE\right)^{(3N-1)/2}$

где $\Gamma (.)$ – гамма-функция , а фактор $N!$ был включен для объяснения неразличимости частиц (см. парадокс Гиббса ). В большом $N$ предел, энтропия Больцмана $S=k_{\mathrm {B} }\log W$ является

$S=k_{\rm {B}}N\log \left[{\frac {V}{N}}\left({\frac {4\pi m}{3}}{\frac {E}{N}}\right)^{3/2}\right]+{\frac {5}{2}}k_{\rm {B}}N+O\left(\log N\right)$

Это также известно как уравнение Сакура – ​​Тетроде .

Температура определяется выражением

${\frac {1}{T}}\equiv {\frac {\partial S}{\partial E}}={\frac {3}{2}}{\frac {Nk_{\mathrm {B} }}{E}}$

что согласуется с аналогичным результатом кинетической теории газов . Вычисление давления дает закон идеального газа :

${\frac {p}{T}}\equiv {\frac {\partial S}{\partial V}}={\frac {Nk_{\mathrm {B} }}{V}}\quad \rightarrow \quad pV=Nk_{\mathrm {B} }T$

Наконец, химический потенциал $\mu$ является

$\mu \equiv -T{\frac {\partial S}{\partial N}}=k_{\rm {B}}T\log \left[{\frac {V}{N}}\,\left({\frac {4\pi mE}{3N}}\right)^{3/2}\right]$

Идеальный газ в однородном гравитационном поле

Микроканонический фазовый объем также может быть рассчитан явно для идеального газа в однородном гравитационном поле .

Результаты изложены ниже для трехмерного идеального газа $N$ частицы, каждая с массой $m$, заключенный в термически изолированный контейнер, который имеет бесконечную длину в направлении z и постоянную площадь поперечного сечения. $A$. Предполагается, что гравитационное поле действует в направлении минус z с напряженностью $g$. Фазовый объем $W(E,N)$ является

$W(E,N)={\frac {(2\pi )^{3N/2}A^{N}m^{N/2}}{g^{N}\Gamma (5N/2)}}E^{{\frac {5N}{2}}-1}$

где $E$ это полная энергия, кинетическая плюс гравитационная.

Плотность газа $\rho (z)$ как функция высоты $z$ можно получить интегрированием по координатам фазового объема. Результат:

$\rho (z)=\left({\frac {5N}{2}}-1\right){\frac {mg}{E}}\left(1-{\frac {mgz}{E}}\right)^{{\frac {5N}{2}}-2}$

Аналогично распределение величины скорости $|{\vec {v}}|$ (среднее по всем высотам) составляет

$f(|{\vec {v}}|)={\frac {\Gamma (5N/2)}{\Gamma (3/2)\Gamma (5N/2-3/2)}}\times {\frac {m^{3/2}|{\vec {v}}|^{2}}{2^{1/2}E^{3/2}}}\times \left(1-{\frac {m|{\vec {v}}|^{2}}{2E}}\right)^{\frac {5(N-1)}{2}}$

Аналогами этих уравнений в каноническом ансамбле являются барометрическая формула и распределение Максвелла–Больцмана соответственно. В пределе $N\rightarrow \infty$, микроканоническое и каноническое выражения совпадают; однако они различаются для конечных $N$. В частности, в микроканоническом ансамбле положения и скорости не являются статистически независимыми. В результате кинетическая температура, определяемая как средняя кинетическая энергия в данном объеме $A\,dz$, неоднороден по всему контейнеру:

$T_{\mathrm {kinetic} }={\frac {3E}{5N-2}}\left(1-{\frac {mgz}{E}}\right)$

Напротив, в каноническом ансамбле температура однородна для любого $N$.

См. также

• Изолированная система
• Эргодическая гипотеза
• Парадокс Лошмидта
• Канонический ансамбль
• Большой канонический ансамбль