Гамма-функция

Чтобы узнать о гамма-функции ординалов, см. функцию Веблена . Информацию о гамма-распределении в статистике см. в разделе Гамма-распределение . Информацию о функции, используемой в представлениях цвета видео и изображений, см. в разделе Гамма-коррекция .

Гамма
Гамма-функция вдоль части вещественной оси
Общая информация
Общее определение	$\Gamma (z)=\int _{0}^{\infty }t^{z-1}e^{-t}\,dt$
Области применения	Исчисление, математический анализ, статистика, физика

В математике гамма -функция (представленная Γ , заглавной буквой «гамма» греческого алфавита ) является одним из широко используемых расширений факториала для комплексных чисел . Гамма-функция определена для всех комплексных чисел, кроме неположительных целых чисел. Для каждого положительного целого n числа

$$\Gamma (n)=(n-1)!\,.$$

Гамма-функция, выведенная Даниэлем Бернулли для комплексных чисел с положительной вещественной частью, определяется через сходящийся несобственный интеграл :

$$\Gamma (z)=\int _{0}^{\infty }t^{z-1}e^{-t}{\text{ d}}t,\ \qquad \Re (z)>0\,.$$

Гамма-функция тогда определяется как аналитическое продолжение этой интегральной функции до мероморфной функции , которая голоморфна во всей комплексной плоскости, за исключением нуля и отрицательных целых чисел, где функция имеет простые полюса .

Гамма-функция не имеет нулей, поэтому обратная гамма-функция 1 / Γ( z ) — целая функция . Фактически гамма-функция соответствует преобразованию Меллина отрицательной показательной функции :

$$\Gamma (z)={\mathcal {M}}\{e^{-x}\}(z)\,.$$

Существуют и другие расширения функции факториала, но гамма-функция является наиболее популярной и полезной. Это компонент различных функций распределения вероятностей, и как таковой он применим в области вероятности и статистики , а также в комбинаторике .

Мотивация

$\Gamma (x+1)$ интерполирует функцию факториала до нецелых значений.

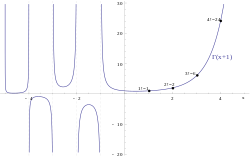
Гамма-функцию можно рассматривать как решение интерполяционной задачи поиска гладкой кривой. $y=f(x)$ который соединяет точки факториала: $(x,y)=(n,n!)$ для всех положительных целых значений $n$. Простая формула факториала x ! = 1 × 2 × ⋯ × x допустимо только тогда, когда x — целое положительное число, и ни одна элементарная функция не обладает этим свойством, но хорошим решением является гамма-функция. $f(x)=\Gamma (x+1)$.

Гамма-функция не только гладкая, но и аналитическая (за исключением неположительных целых чисел), и ее можно определить несколькими явными способами. Однако это не единственная аналитическая функция, расширяющая факториал, поскольку можно добавить любую аналитическую функцию, равную нулю для положительных целых чисел, например: $k\sin(m\pi x)$ для целого числа $m$. Такая функция известна как псевдогамма-функция , наиболее известной из которых является функция Адамара .

Гамма-функция Γ( z ) синего цвета изображена вместе с Γ( z ) + sin(π z ) зеленым цветом. Обратите внимание на пересечение положительных целых чисел. Оба являются действительными расширениями факториалов до мероморфной функции на комплексной плоскости.

Более строгим требованием является функциональное уравнение , которое интерполирует сдвинутый факториал. $f(n)=(n{-}1)!$ :

$$f(x+1)=xf(x)\ {\text{ for any }}x>0,\qquad f(1)=1.$$

Но это все равно не дает однозначного решения, так как допускает умножение на любую периодическую функцию $g(x)$ с $g(x)=g(x+1)$ и $g(0)=1$, такой как $g(x)=e^{k\sin(m\pi x)}$. Одним из способов разрешения неоднозначности является теорема Бора – Моллерупа , которая показывает, что $f(x)=\Gamma (x)$ - уникальная интерполирующая функция по положительным числам, которая является логарифмически выпуклой (сверхвыпуклой), это означает, что $y=\ln f(x)$ является выпуклым .

Определение

Основное определение

Обозначения $\Gamma (z)$ это заслуга Лежандра . Если действительная часть комплексного числа z строго положительна ( $\Re (z)>0$), то интеграл

$$\Gamma (z)=\int _{0}^{\infty }t^{z-1}e^{-t}\,dt$$

сходится абсолютно и известен как интеграл Эйлера второго рода . (Интеграл Эйлера первого рода — это бета-функция . ) Используя интегрирование по частям , видим, что:

Абсолютное значение (по вертикали) и аргумент (цвет) гамма-функции на комплексной плоскости.

$${\begin{aligned}\Gamma (z+1)&=\int _{0}^{\infty }t^{z}e^{-t}\,dt\\&={\Bigl [}-t^{z}e^{-t}{\Bigr ]}_{0}^{\infty }+\int _{0}^{\infty }zt^{z-1}e^{-t}\,dt\\&=\lim _{t\to \infty }\left(-t^{z}e^{-t}\right)-\left(-0^{z}e^{-0}\right)+z\int _{0}^{\infty }t^{z-1}e^{-t}\,dt.\end{aligned}}$$

Признавая, что $-t^{z}e^{-t}\to 0$ как $t\to \infty ,$

$${\begin{aligned}\Gamma (z+1)&=z\int _{0}^{\infty }t^{z-1}e^{-t}\,dt\\&=z\Gamma (z).\end{aligned}}$$

Мы можем рассчитать $\Gamma (1)$:

$${\begin{aligned}\Gamma (1)&=\int _{0}^{\infty }t^{1-1}e^{-t}\,dt\\&=\int _{0}^{\infty }e^{-t}\,dt\\&=1.\end{aligned}}$$

Таким образом, мы можем показать, что $\Gamma (n)=(n-1)!$ для любого натурального числа n по индукции . В частности, базовый случай заключается в том, что $\Gamma (1)=1=0!$, а шаг индукции таков: $\Gamma (n+1)=n\Gamma (n)=n(n-1)!=n!.$

Личность ${\textstyle \Gamma (z)={\frac {\Gamma (z+1)}{z}}}$ можно использовать (или, что дает тот же результат, можно использовать аналитическое продолжение ) для однозначного расширения интегральной формулировки для $\Gamma (z)$ к мероморфной функции, определенной для всех комплексных чисел z , кроме целых чисел, меньших или равных нулю. Именно эту расширенную версию обычно называют гамма-функцией.

Альтернативные определения

Существует множество эквивалентных определений.

Эйлера как

Для фиксированного целого числа $m$, как целое число $n$ увеличивается, у нас это есть

$$\lim _{n\to \infty }{\frac {n!\,\left(n+1\right)^{m}}{(n+m)!}}=1\,.$$

Если $m$ не является целым числом, то невозможно сказать, верно ли это уравнение, поскольку мы еще (в этом разделе) не определили функцию факториала для нецелых чисел. Однако мы получаем уникальное расширение функции факториала на нецелые числа, настаивая на том, что это уравнение продолжает выполняться, когда произвольное целое число $m$ заменяется произвольным комплексным числом $z$,

$$\lim _{n\to \infty }{\frac {n!\,\left(n+1\right)^{z}}{(n+z)!}}=1\,.$$

Умножив обе части на $(z-1)!$ дает

$${\begin{aligned}\Gamma (z)&=(z-1)!\\[8pt]&={\frac {1}{z}}\lim _{n\to \infty }n!{\frac {z!}{(n+z)!}}(n+1)^{z}\\[8pt]&={\frac {1}{z}}\lim _{n\to \infty }(1\cdots n){\frac {1}{(1+z)\cdots (n+z)}}\left({\frac {2}{1}}\cdot {\frac {3}{2}}\cdots {\frac {n+1}{n}}\right)^{z}\\[8pt]&={\frac {1}{z}}\prod _{n=1}^{\infty }\left[{\frac {1}{1+{\frac {z}{n}}}}\left(1+{\frac {1}{n}}\right)^{z}\right].\end{aligned}}$$

Это бесконечное произведение , принадлежащее Эйлеру, сходится для всех комплексных чисел $z$ за исключением неположительных целых чисел, которые терпят неудачу из-за деления на ноль. Интуитивно эта формула показывает, что $\Gamma (z)$ примерно является результатом вычислений $\Gamma (n+1)=n!$ для некоторого большого целого числа $n$, умножив на $(n+1)^{z}$ приблизить $\Gamma (n+z+1)$, и используя отношение $\Gamma (x+1)=x\Gamma (x)$ назад $n+1$ раз, чтобы получить приблизительное значение $\Gamma (z)$; и, более того, это приближение становится точным как $n$ увеличивается до бесконечности.

Определение Вейерштрасса

Определение гамма-функции, данное Вейерштрассом, также справедливо для всех комплексных чисел z, кроме неположительных целых чисел:

$$\Gamma (z)={\frac {e^{-\gamma z}}{z}}\prod _{n=1}^{\infty }\left(1+{\frac {z}{n}}\right)^{-1}e^{z/n},$$

где $\gamma \approx 0.577216$ – постоянная Эйлера–Машерони . Это Адамара произведение $1/\Gamma (z)$ в переписанном виде. Полезность этого определения невозможно переоценить, поскольку она проявляется в определенном тождестве, включающем число Пи.

show Доказательство эквивалентности трех определений

Equivalence of the integral definition and Weierstrass definition By the integral definition, the relation $\Gamma (z+1)=z\Gamma (z)$ and Hadamard factorization theorem, $${\frac {1}{\Gamma (z)}}=ze^{c_{1}z+c_{2}}\prod _{n=1}^{\infty }e^{-{\frac {z}{n}}}\left(1+{\frac {z}{n}}\right),\quad z\in \mathbb {C} \setminus \mathbb {Z} _{0}^{-}$$ for some constants $c_{1},c_{2}$ since $1/\Gamma$ is an entire function of order $1$. Since $z\Gamma (z)\to 1$ as $z\to 0$, $c_{2}=0$ (or an integer multiple of $2\pi i$) and since $\Gamma (1)=1$, $${\begin{aligned}e^{-c_{1}}&=\prod _{n=1}^{\infty }e^{-{\frac {1}{n}}}\left(1+{\frac {1}{n}}\right)\\&=\exp \left(\lim _{N\to \infty }\sum _{n=1}^{N}\left(\log \left(1+{\frac {1}{n}}\right)-{\frac {1}{n}}\right)\right)\\&=\exp \left(\lim _{N\to \infty }\left(\log(N+1)-\sum _{n=1}^{N}{\frac {1}{n}}\right)\right)\\&=\exp \left(\lim _{N\to \infty }\left(\log N+\log \left(1+{\frac {1}{N}}\right)-\sum _{n=1}^{N}{\frac {1}{n}}\right)\right)\\&=\exp \left(\lim _{N\to \infty }\left(\log N-\sum _{n=1}^{N}{\frac {1}{n}}\right)\right)\\&=e^{-\gamma }.\end{aligned}}$$ Whence $c_{1}=\gamma +2\pi ik$ for some integer $k$. Since $\Gamma (z)\in \mathbb {R}$ for $z\in \mathbb {R} \setminus \mathbb {Z} _{0}^{-}$, we have $k=0$ and $${\frac {1}{\Gamma (z)}}=ze^{\gamma z}\prod _{n=1}^{\infty }e^{-{\frac {z}{n}}}\left(1+{\frac {z}{n}}\right),\quad z\in \mathbb {C} \setminus \mathbb {Z} _{0}^{-}.$$ Equivalence of the Weierstrass definition and Euler definition $${\begin{aligned}\Gamma (z)&={\frac {e^{-\gamma z}}{z}}\prod _{n=1}^{\infty }\left(1+{\frac {z}{n}}\right)^{-1}e^{z/n}\\&={\frac {1}{z}}\lim _{n\to \infty }e^{z\left(\ln n-1-{\frac {1}{2}}-{\frac {1}{3}}-\cdots -{\frac {1}{n}}\right)}{\frac {e^{z\left(1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}\right)}}{\left(1+z\right)\left(1+{\frac {z}{2}}\right)\cdots \left(1+{\frac {z}{n}}\right)}}\\&={\frac {1}{z}}\lim _{n\to \infty }{\frac {1}{\left(1+z\right)\left(1+{\frac {z}{2}}\right)\cdots \left(1+{\frac {z}{n}}\right)}}e^{z\ln \left(n\right)}\\&=\lim _{n\to \infty }{\frac {n!n^{z}}{z(z+1)\cdots (z+n)}},\quad z\in \mathbb {C} \setminus \mathbb {Z} _{0}^{-}\end{aligned}}$$ Let $$\Gamma _{n}(z)={\frac {n!n^{z}}{z(z+1)\cdots (z+n)}}$$ and $$G_{n}(z)={\frac {(n-1)!n^{z}}{z(z+1)\cdots (z+n-1)}}.$$ Then $$\Gamma _{n}(z)={\frac {n}{z+n}}G_{n}(z)$$ and $$\lim _{n\to \infty }G_{n+1}(z)=\lim _{n\to \infty }G_{n}(z)=\lim _{n\to \infty }\Gamma _{n}(z)=\Gamma (z),$$ therefore $$\Gamma (z)=\lim _{n\to \infty }{\frac {n!(n+1)^{z}}{z(z+1)\cdots (z+n)}},\quad z\in \mathbb {C} \setminus \mathbb {Z} _{0}^{-}.$$ Then $${\frac {n!(n+1)^{z}}{z(z+1)\cdots (z+n)}}={\frac {(2/1)^{z}(3/2)^{z}(4/3)^{z}\cdots ((n+1)/n)^{z}}{z(1+z)(1+z/2)(1+z/3)\cdots (1+z/n)}}={\frac {1}{z}}\prod _{k=1}^{n}{\frac {(1+1/k)^{z}}{1+z/k}},\quad z\in \mathbb {C} \setminus \mathbb {Z} _{0}^{-}$$ and taking $n\to \infty$ gives the desired result.

Свойства

Общие

Помимо фундаментального свойства, обсуждавшегося выше:

$$\Gamma (z+1)=z\ \Gamma (z)$$

другими важными функциональными уравнениями для гамма-функции являются формула отражения Эйлера.

$$\Gamma (1-z)\Gamma (z)={\frac {\pi }{\sin \pi z}},\qquad z\not \in \mathbb {Z}$$

что подразумевает

$$\Gamma (z-n)=(-1)^{n-1}\;{\frac {\Gamma (-z)\Gamma (1+z)}{\Gamma (n+1-z)}},\qquad n\in \mathbb {Z}$$

и формула дублирования Лежандра

$$\Gamma (z)\Gamma \left(z+{\tfrac {1}{2}}\right)=2^{1-2z}\;{\sqrt {\pi }}\;\Gamma (2z).$$

show Вывод формулы отражения Эйлера

Proof 1 We can use Euler's infinite product $$\Gamma (z)={\frac {1}{z}}\prod _{n=1}^{\infty }{\frac {(1+1/n)^{z}}{1+z/n}}$$ to compute $${\frac {1}{\Gamma (1-z)\Gamma (z)}}={\frac {1}{(-z)\Gamma (-z)\Gamma (z)}}=z\prod _{n=1}^{\infty }{\frac {(1-z/n)(1+z/n)}{(1+1/n)^{-z}(1+1/n)^{z}}}=z\prod _{n=1}^{\infty }\left(1-{\frac {z^{2}}{n^{2}}}\right)={\frac {\sin \pi z}{\pi }}\,,$$ where the last equality is a known result. A similar derivation begins with Weierstrass's definition. Proof 2 First we prove that $$I=\int _{-\infty }^{\infty }{\frac {e^{ax}}{1+e^{x}}}\,dx=\int _{0}^{\infty }{\frac {v^{a-1}}{1+v}}\,dv={\frac {\pi }{\sin \pi a}},\quad a\in (0,1).$$ Consider the positively oriented rectangular contour $C_{R}$ with vertices at $R$, $-R$, $R+2\pi i$ and $-R+2\pi i$ where $R\in \mathbb {R} ^{+}$. Then by the residue theorem, $$\int _{C_{R}}{\frac {e^{az}}{1+e^{z}}}\,dz=-2\pi ie^{a\pi i}.$$ Let $$I_{R}=\int _{-R}^{R}{\frac {e^{ax}}{1+e^{x}}}\,dx$$ and let $I_{R}'$ be the analogous integral over the top side of the rectangle. Then $I_{R}\to I$ as $R\to \infty$ and $I_{R}'=-e^{2\pi ia}I_{R}$. If $A_{R}$ denotes the right vertical side of the rectangle, then $$\left|\int _{A_{R}}{\frac {e^{az}}{1+e^{z}}}\,dz\right|\leq \int _{0}^{2\pi }\left|{\frac {e^{a(R+it)}}{1+e^{R+it}}}\right|\,dt\leq Ce^{(a-1)R}$$ for some constant $C$ and since $a<1$, the integral tends to $0$ as $R\to \infty$. Analogously, the integral over the left vertical side of the rectangle tends to $0$ as $R\to \infty$. Therefore $$I-e^{2\pi ia}I=-2\pi ie^{a\pi i},$$ from which $$I={\frac {\pi }{\sin \pi a}},\quad a\in (0,1).$$ Then $$\Gamma (1-z)=\int _{0}^{\infty }e^{-u}u^{-z}\,du=t\int _{0}^{\infty }e^{-vt}(vt)^{-z}\,dv,\quad t>0$$ and $${\begin{aligned}\Gamma (z)\Gamma (1-z)&=\int _{0}^{\infty }\int _{0}^{\infty }e^{-t(1+v)}v^{-z}\,dv\,dt\\&=\int _{0}^{\infty }{\frac {v^{-z}}{1+v}}\,dv\\&={\frac {\pi }{\sin \pi (1-z)}}\\&={\frac {\pi }{\sin \pi z}},\quad z\in (0,1).\end{aligned}}$$ Proving the reflection formula for all $z\in (0,1)$ proves it for all $z\in \mathbb {C} \setminus \mathbb {Z}$ by analytic continuation.

show Вывод формулы дублирования Лежандра

The beta function can be represented as $$\mathrm {B} (z_{1},z_{2})={\frac {\Gamma (z_{1})\Gamma (z_{2})}{\Gamma (z_{1}+z_{2})}}=\int _{0}^{1}t^{z_{1}-1}(1-t)^{z_{2}-1}\,dt.$$ Setting $z_{1}=z_{2}=z$ yields $${\frac {\Gamma ^{2}(z)}{\Gamma (2z)}}=\int _{0}^{1}t^{z-1}(1-t)^{z-1}\,dt.$$ After the substitution $t={\frac {1+u}{2}}$ we get $${\frac {\Gamma ^{2}(z)}{\Gamma (2z)}}={\frac {1}{2^{2z-1}}}\int _{-1}^{1}\left(1-u^{2}\right)^{z-1}\,du.$$ The function $(1-u^{2})^{z-1}$ is even, hence $$2^{2z-1}\Gamma ^{2}(z)=2\Gamma (2z)\int _{0}^{1}(1-u^{2})^{z-1}\,du.$$ Now assume $$\mathrm {B} \left({\frac {1}{2}},z\right)=\int _{0}^{1}t^{{\frac {1}{2}}-1}(1-t)^{z-1}\,dt,\quad t=s^{2}.$$ Then $$\mathrm {B} \left({\frac {1}{2}},z\right)=2\int _{0}^{1}(1-s^{2})^{z-1}\,ds=2\int _{0}^{1}(1-u^{2})^{z-1}\,du.$$ This implies $$2^{2z-1}\Gamma ^{2}(z)=\Gamma (2z)\mathrm {B} \left({\frac {1}{2}},z\right).$$ Since $$\mathrm {B} \left({\frac {1}{2}},z\right)={\frac {\Gamma \left({\frac {1}{2}}\right)\Gamma (z)}{\Gamma \left(z+{\frac {1}{2}}\right)}},\quad \Gamma \left({\frac {1}{2}}\right)={\sqrt {\pi }},$$ the Legendre duplication formula follows: $$\Gamma (z)\Gamma \left(z+{\frac {1}{2}}\right)=2^{1-2z}{\sqrt {\pi }}\;\Gamma (2z).$$

Формула умножения является частным случаем теоремы умножения (см. уравнение 5.5.6):

$$\prod _{k=0}^{m-1}\Gamma \left(z+{\frac {k}{m}}\right)=(2\pi )^{\frac {m-1}{2}}\;m^{{\frac {1}{2}}-mz}\;\Gamma (mz).$$

Простое, но полезное свойство, которое можно увидеть из определения предела:

$${\overline {\Gamma (z)}}=\Gamma ({\overline {z}})\;\Rightarrow \;\Gamma (z)\Gamma ({\overline {z}})\in \mathbb {R} .$$

В частности, при z = a + bi это произведение

$$|\Gamma (a+bi)|^{2}=|\Gamma (a)|^{2}\prod _{k=0}^{\infty }{\frac {1}{1+{\frac {b^{2}}{(a+k)^{2}}}}}$$

Если действительная часть является целым или полуцелым числом, это можно конечно выразить в замкнутой форме :

$${\begin{aligned}|\Gamma (bi)|^{2}&={\frac {\pi }{b\sinh \pi b}}\\[1ex]\left|\Gamma \left({\tfrac {1}{2}}+bi\right)\right|^{2}&={\frac {\pi }{\cosh \pi b}}\\[1ex]\left|\Gamma \left(1+bi\right)\right|^{2}&={\frac {\pi b}{\sinh \pi b}}\\[1ex]\left|\Gamma \left(1+n+bi\right)\right|^{2}&={\frac {\pi b}{\sinh \pi b}}\prod _{k=1}^{n}\left(k^{2}+b^{2}\right),\quad n\in \mathbb {N} \\[1ex]\left|\Gamma \left(-n+bi\right)\right|^{2}&={\frac {\pi }{b\sinh \pi b}}\prod _{k=1}^{n}\left(k^{2}+b^{2}\right)^{-1},\quad n\in \mathbb {N} \\[1ex]\left|\Gamma \left({\tfrac {1}{2}}\pm n+bi\right)\right|^{2}&={\frac {\pi }{\cosh \pi b}}\prod _{k=1}^{n}\left(\left(k-{\tfrac {1}{2}}\right)^{2}+b^{2}\right)^{\pm 1},\quad n\in \mathbb {N} \\[-1ex]&\end{aligned}}$$

show Доказательство формул абсолютного значения для аргументов целой или полуцелой действительной части

First, consider the reflection formula applied to $z=bi$. $$\Gamma (bi)\Gamma (1-bi)={\frac {\pi }{\sin \pi bi}}$$ Applying the recurrence relation to the second term, we have $$-bi\cdot \Gamma (bi)\Gamma (-bi)={\frac {\pi }{\sin \pi bi}}$$ which with simple rearrangement gives $$\Gamma (bi)\Gamma (-bi)={\frac {\pi }{-bi\sin \pi bi}}={\frac {\pi }{b\sinh \pi b}}$$ Second, consider the reflection formula applied to $z={\tfrac {1}{2}}+bi$. $$\Gamma ({\tfrac {1}{2}}+bi)\Gamma \left(1-({\tfrac {1}{2}}+bi)\right)=\Gamma ({\tfrac {1}{2}}+bi)\Gamma ({\tfrac {1}{2}}-bi)={\frac {\pi }{\sin \pi ({\tfrac {1}{2}}+bi)}}={\frac {\pi }{\cos \pi bi}}={\frac {\pi }{\cosh \pi b}}$$ Formulas for other values of $z$ for which the real part is integer or half-integer quickly follow by induction using the recurrence relation in the positive and negative directions.

Возможно, самое известное значение гамма-функции при нецелом аргументе:

$$\Gamma \left({\tfrac {1}{2}}\right)={\sqrt {\pi }},$$

который можно найти, установив ${\textstyle z={\frac {1}{2}}}$ в формулах отражения или дублирования, используя приведенное ниже отношение к бета-функции с ${\textstyle z_{1}=z_{2}={\frac {1}{2}}}$или просто сделав замену $u={\sqrt {z}}$ в интегральном определении гамма-функции, что приводит к интегралу Гаусса . В общем, для неотрицательных целых значений $n$ у нас есть:

$${\begin{aligned}\Gamma \left({\tfrac {1}{2}}+n\right)&={(2n)! \over 4^{n}n!}{\sqrt {\pi }}={\frac {(2n-1)!!}{2^{n}}}{\sqrt {\pi }}={\binom {n-{\frac {1}{2}}}{n}}n!{\sqrt {\pi }}\\[8pt]\Gamma \left({\tfrac {1}{2}}-n\right)&={(-4)^{n}n! \over (2n)!}{\sqrt {\pi }}={\frac {(-2)^{n}}{(2n-1)!!}}{\sqrt {\pi }}={\frac {\sqrt {\pi }}{{\binom {-1/2}{n}}n!}}\end{aligned}}$$

где двойной факториал $(2n-1)!!=(2n-1)(2n-3)\cdots (3)(1)$. см . в разделе «Особые значения гамма-функции» Расчетные значения .

Может возникнуть соблазн обобщить результат, ${\textstyle \Gamma \left({\frac {1}{2}}\right)={\sqrt {\pi }}}$ путем поиска формулы для других индивидуальных значений $\Gamma (r)$ где $r$ является рациональным, особенно потому, что согласно дигамм-теореме Гаусса это возможно сделать для близкородственной дигамма-функции при каждом рациональном значении. Однако эти цифры $\Gamma (r)$ неизвестно, что они выражаются сами по себе через элементарные функции. Было доказано, что $\Gamma (n+r)$ является трансцендентным числом и алгебраически не зависит от $\pi$ для любого целого числа $n$ и каждая из фракций ${\textstyle r={\frac {1}{6}},{\frac {1}{4}},{\frac {1}{3}},{\frac {2}{3}},{\frac {3}{4}},{\frac {5}{6}}}$. В общем, при вычислении значений гамма-функции мы должны использовать численные аппроксимации.

Производные гамма-функции описываются через полигамма- функцию ψ ⁽⁰⁾ ( С ) :

$$\Gamma '(z)=\Gamma (z)\psi ^{(0)}(z).$$

Для положительного целого числа m производную гамма-функции можно вычислить следующим образом:

Цвета, показывающие аргумент гамма-функции в комплексной плоскости от −2 − 2 i до 6 + 2 i.

$$\Gamma '(m+1)=m!\left(-\gamma +\sum _{k=1}^{m}{\frac {1}{k}}\right)=m!\left(-\gamma +H(m)\right)\,,$$

где H(m) — номер m-й гармоники , а γ — константа Эйлера–Машерони .

Для $\Re (z)>0$ тот $n$-я производная гамма-функции:

$${\frac {d^{n}}{dz^{n}}}\Gamma (z)=\int _{0}^{\infty }t^{z-1}e^{-t}(\ln t)^{n}\,dt.$$

(Это можно получить, дифференцируя интегральную форму гамма-функции по $z$, и используя технику дифференцирования под знаком интеграла .)

Использование личности

$$\Gamma ^{(n)}(1)=(-1)^{n}B_{n}(\gamma ,1!\zeta (2),\ldots ,(n-1)!\zeta (n))$$

где $\zeta (z)$ – дзета-функция Римана , и $B_{n}$ это $n$-го полинома Белла , мы имеем, в частности, разложение в ряд Лорана гамма-функции

$$\Gamma (z)={\frac {1}{z}}-\gamma +{\frac {1}{2}}\left(\gamma ^{2}+{\frac {\pi ^{2}}{6}}\right)z-{\frac {1}{6}}\left(\gamma ^{3}+{\frac {\gamma \pi ^{2}}{2}}+2\zeta (3)\right)z^{2}+O(z^{3}).$$

Неравенства

Если ограничиться положительными действительными числами, гамма-функция является строго логарифмически выпуклой функцией . Это свойство может быть выражено любым из следующих трех эквивалентных способов:

• Для любых двух положительных действительных чисел $x_{1}$ и $x_{2}$, и для любого $t\in [0,1]$,
  $$\Gamma (tx_{1}+(1-t)x_{2})\leq \Gamma (x_{1})^{t}\Gamma (x_{2})^{1-t}.$$
• Для любых двух положительных действительных чисел $x_{1}$ и $x_{2}$, и $x_{2}$ > $x_{1}$
  $$\left({\frac {\Gamma (x_{2})}{\Gamma (x_{1})}}\right)^{\frac {1}{x_{2}-x_{1}}}>\exp \left({\frac {\Gamma '(x_{1})}{\Gamma (x_{1})}}\right).$$
• Для любого положительного действительного числа $x$,
  $$\Gamma ''(x)\Gamma (x)>\Gamma '(x)^{2}.$$

Последнее из этих утверждений, по сути, по определению то же самое, что утверждение о том, что $\psi ^{(1)}(x)>0$, где $\psi ^{(1)}$ – полигамма-функция первого порядка. Поэтому для доказательства логарифмической выпуклости гамма-функции достаточно заметить, что $\psi ^{(1)}$ имеет серийное представление, которое для положительных вещественных x состоит только из положительных членов.

Логарифмическая выпуклость и неравенство Йенсена вместе означают, что для любых положительных действительных чисел $x_{1},\ldots ,x_{n}$ и $a_{1},\ldots ,a_{n}$,

$$\Gamma \left({\frac {a_{1}x_{1}+\cdots +a_{n}x_{n}}{a_{1}+\cdots +a_{n}}}\right)\leq {\bigl (}\Gamma (x_{1})^{a_{1}}\cdots \Gamma (x_{n})^{a_{n}}{\bigr )}^{\frac {1}{a_{1}+\cdots +a_{n}}}.$$

Существуют также границы на отношения гамма-функций. Самым известным является неравенство Гаучи , которое гласит, что для любого положительного действительного числа x и любого s ∈ (0, 1 )

$$x^{1-s}<{\frac {\Gamma (x+1)}{\Gamma (x+s)}}<\left(x+1\right)^{1-s}.$$

Формула Стирлинга

Основная статья: Приближение Стирлинга

Представление гамма-функции в комплексной плоскости. Каждая точка $z$ раскрашивается в соответствии с аргументом $\Gamma (z)$. Контурный график модуля $|\Gamma (z)|$ также отображается.

Трехмерный график абсолютного значения комплексной гамма-функции

Поведение $\Gamma (x)$ для возрастающей положительной действительной переменной определяется формулой Стирлинга

$$\Gamma (x+1)\sim {\sqrt {2\pi x}}\left({\frac {x}{e}}\right)^{x},$$

где символ $\sim$ означает асимптотическую сходимость: отношение двух сторон сходится к 1 в пределе ${\textstyle x\to +\infty }$. Этот рост быстрее, чем экспоненциальный, $\exp(\beta x)$, для любого фиксированного значения $\beta$.

Еще один полезный предел асимптотических приближений для $x\to +\infty$ является:

$${\Gamma (x+\alpha )}\sim {\Gamma (x)x^{\alpha }},\qquad \alpha \in \mathbb {C} .$$

При записи члена ошибки в виде бесконечного произведения для определения гамма-функции можно использовать формулу Стирлинга:

$$\Gamma \left(x\right)={\sqrt {\frac {2\pi }{x}}}{\frac {x}{e}}^{x}\prod _{n=0}^{\infty }e^{-1}\left(1+{\frac {1}{x+n}}\right)^{{\frac {1}{2}}+x+n}$$

Остатки

Поведение для неположительных $z$ является более сложным. Интеграл Эйлера не сходится при $\Re (z)\leq 0$, но функция, которую он определяет в положительной комплексной полуплоскости, имеет единственное аналитическое продолжение в отрицательную полуплоскость. Один из способов найти это аналитическое продолжение - использовать интеграл Эйлера для положительных аргументов и расширить область определения до отрицательных чисел путем многократного применения рекуррентной формулы:

$$\Gamma (z)={\frac {\Gamma (z+n+1)}{z(z+1)\cdots (z+n)}},$$

выбирая $n$ такой, что $z+n$ является положительным. Произведение в знаменателе равно нулю, если $z$ равно любому из целых чисел $0,-1,-2,\ldots$. Таким образом, гамма-функция должна быть неопределенной в этих точках, чтобы избежать деления на ноль ; это мероморфная функция с простыми полюсами в неположительных целых числах.

Для функции $f$ комплексной переменной $z$, на простом полюсе $c$, остаток ​ $f$ дается:

$$\operatorname {Res} (f,c)=\lim _{z\to c}(z-c)f(z).$$

Для простого шеста $z=-n,$ перепишем рекуррентную формулу так:

$$(z+n)\Gamma (z)={\frac {\Gamma (z+n+1)}{z(z+1)\cdots (z+n-1)}}.$$

Числитель в $z=-n,$ является

$$\Gamma (z+n+1)=\Gamma (1)=1$$

и знаменатель

$$z(z+1)\cdots (z+n-1)=-n(1-n)\cdots (n-1-n)=(-1)^{n}n!.$$

Таким образом, остатки гамма-функции в этих точках равны:

$$\operatorname {Res} (\Gamma ,-n)={\frac {(-1)^{n}}{n!}}.$$

Гамма-функция отлична от нуля всюду вдоль вещественной линии, хотя при z → −∞ она сколь угодно близка к нулю . На самом деле не существует комплексного числа $z$ для чего $\Gamma (z)=0$, и, следовательно, обратная гамма-функция ${\textstyle {\frac {1}{\Gamma (z)}}}$ целая функция с нулями в $z=0,-1,-2,\ldots$.

Минимумы и максимумы

На реальной линии гамма-функция имеет локальный минимум при z _min ≈ +1,46163 21449 68362 34126 где оно достигает значения Γ( z _min ) ≈ +0,88560 31944 10888 70027 . Гамма-функция возрастает по обе стороны от этого минимума. Решением Γ( z − 0,5) = Γ( z + 0,5) является z = +1,5 , а общее значение — Γ(1) = Γ(2) = +1 . Положительное решение задачи Γ( z − 1) = Γ( z + 1) — это z = φ ≈ +1,618 , золотое сечение , а общее значение — Γ( φ − 1) = Γ( φ + 1) = φ ! ≈ +1.44922 96022 69896 60037 .

Гамма-функция должна менять знак между своими полюсами в неположительных целых числах, поскольку произведение в прямой рекуррентности содержит нечетное количество отрицательных факторов, если количество полюсов между $z$ и $z+n$ нечетное и четное число, если число полюсов четное. Значения локальных экстремумов гамма-функции вдоль действительной оси между неположительными целыми числами:

С( -0,50408 30082 64455 40925... ) = −3.54464 36111 55005 08912... ,

С( -1,57349 84731 62390 45877... ) = 2.30240 72583 39680 13582... ,

С( -2,61072 08684 44144 65000... ) = −0.88813 63584 01241 92009... ,

С( -3,63529 33664 36901 09783... ) = 0.24512 75398 34366 25043... ,

С( -4,65323 77617 43142 44171... ) = −0,05277 96395 87319 40076... и т. д.

Интегральные представления

Существует множество формул, помимо интеграла Эйлера второго рода, выражающих гамма-функцию в виде интеграла. Например, когда действительная часть z положительна,

$$\Gamma (z)=\int _{-\infty }^{\infty }e^{zt-e^{t}}\,dt$$

и

$$\Gamma (z)=\int _{0}^{1}\left(\log {\frac {1}{t}}\right)^{z-1}\,dt,$$

$$\Gamma (z)=2\int _{0}^{\infty }t^{2z-1}e^{-t^{2}}\,dt$$

где три интеграла соответственно следуют из замен $t=e^{-x}$, $t=-\log x$ и $t=x^{2}$ во втором интеграле Эйлера. Последний интеграл, в частности, проясняет связь между гамма-функцией при полуцелых аргументах и ​​интегралом Гаусса : если мы допустим $z=1/2$ мы получаем ${\textstyle \Gamma (1/2)={\sqrt {\pi }}=2\int _{0}^{\infty }e^{-t^{2}}\,dt}$.

Первая интегральная формула Бине для гамма-функции гласит, что, когда действительная часть z положительна, тогда:

$$\log \Gamma (z)=\left(z-{\frac {1}{2}}\right)\log z-z+{\frac {1}{2}}\log(2\pi )+\int _{0}^{\infty }\left({\frac {1}{2}}-{\frac {1}{t}}+{\frac {1}{e^{t}-1}}\right){\frac {e^{-tz}}{t}}\,dt.$$

Интеграл в правой части можно интерпретировать как преобразование Лапласа . То есть,

$$\log \left(\Gamma (z)\left({\frac {e}{z}}\right)^{z}{\sqrt {2\pi z}}\right)={\mathcal {L}}\left({\frac {1}{2t}}-{\frac {1}{t^{2}}}+{\frac {1}{t(e^{t}-1)}}\right)(z).$$

Вторая интегральная формула Бине утверждает, что, опять же, когда действительная часть z положительна, тогда:

$$\log \Gamma (z)=\left(z-{\frac {1}{2}}\right)\log z-z+{\frac {1}{2}}\ln(2\pi )+2\int _{0}^{\infty }{\frac {\arctan(t/z)}{e^{2\pi t}-1}}\,dt.$$

Пусть C — контур Ганкеля , означающий путь, который начинается и заканчивается в точке ∞ на сфере Римана , единичный касательный вектор которого сходится к −1 в начале пути и к 1 в конце, который имеет номер обмотки 1 вокруг 0 и который не пересекает [0, ∞) . Исправить ветку $\log(-t)$ разрезав ветвь вдоль [0, ∞) и взяв $\log(-t)$ быть действительным, когда t находится на отрицательной действительной оси. Предположим, что z не является целым числом. Тогда формула Ханкеля для гамма-функции:

$$\Gamma (z)=-{\frac {1}{2i\sin \pi z}}\int _{C}(-t)^{z-1}e^{-t}\,dt,$$

где $(-t)^{z-1}$ интерпретируется как $\exp((z-1)\log(-t))$. Формула отражения приводит к тесно связанному выражению

$${\frac {1}{\Gamma (z)}}={\frac {i}{2\pi }}\int _{C}(-t)^{-z}e^{-t}\,dt,$$

снова допустимо, если z не является целым числом.

Представление непрерывной дроби

Гамма-функцию также можно представить в виде суммы двух цепных дробей :

$$\Gamma (z)={\cfrac {e^{-1}}{2+0-z+1{\cfrac {z-1}{2+2-z+2{\cfrac {z-2}{2+4-z+3{\cfrac {z-3}{2+6-z+4{\cfrac {z-4}{2+8-z+5{\cfrac {z-5}{2+10-z+\ddots }}}}}}}}}}}}+{\cfrac {e^{-1}}{z+0-{\cfrac {z+0}{z+1+{\cfrac {1}{z+2-{\cfrac {z+1}{z+3+{\cfrac {2}{z+4-{\cfrac {z+2}{z+5+{\cfrac {3}{z+6-\ddots }}}}}}}}}}}}}}$$

где $z\in \mathbb {C}$.

Фурье

Логарифм гамма-функции имеет следующее разложение в ряд Фурье для $0<z<1:$

$$\ln \Gamma (z)=\left({\frac {1}{2}}-z\right)(\gamma +\ln 2)+(1-z)\ln \pi -{\frac {1}{2}}\ln \sin(\pi z)+{\frac {1}{\pi }}\sum _{n=1}^{\infty }{\frac {\ln n}{n}}\sin(2\pi nz),$$

которое долгое время приписывалось Эрнсту Куммеру , выведшему его в 1847 году. Однако Ярослав Благоушин обнаружил, что Карл Йохан Мальмстен впервые вывел этот ряд в 1842 году.

Формула Раабе

В 1840 году Йозеф Людвиг Раабе доказал, что

$$\int _{a}^{a+1}\ln \Gamma (z)\,dz={\tfrac {1}{2}}\ln 2\pi +a\ln a-a,\quad a>0.$$

В частности, если $a=0$ затем

$$\int _{0}^{1}\ln \Gamma (z)\,dz={\tfrac {1}{2}}\ln 2\pi .$$

Последнее можно получить, логарифмируя приведенную выше формулу умножения, которая дает выражение суммы Римана подынтегральной функции. Берем лимит на $a\to \infty$ дает формулу.

Функция Пи

Альтернативное обозначение, первоначально введенное Гауссом, — это $\Pi$-функция, которая в терминах гамма-функции равна

$$\Pi (z)=\Gamma (z+1)=z\Gamma (z)=\int _{0}^{\infty }e^{-t}t^{z}\,dt,$$

так что $\Pi (n)=n!$ для каждого неотрицательного целого числа $n$.

Используя функцию пи, формула отражения принимает вид

$$\Pi (z)\Pi (-z)={\frac {\pi z}{\sin(\pi z)}}={\frac {1}{\operatorname {sinc} (z)}}$$

где sinc — нормированная функция sinc , а теорема умножения принимает вид

$$\Pi \left({\frac {z}{m}}\right)\,\Pi \left({\frac {z-1}{m}}\right)\cdots \Pi \left({\frac {z-m+1}{m}}\right)=(2\pi )^{\frac {m-1}{2}}m^{-z-{\frac {1}{2}}}\Pi (z)\ .$$

Мы также иногда находим

$$\pi (z)={\frac {1}{\Pi (z)}}\ ,$$

которая представляет собой целую функцию , определенную для каждого комплексного числа, точно так же, как обратная гамма-функция . Что $\pi (z)$ является целым, значит, у него нет полюсов, поэтому $\Pi \left(z\right)$, нравиться $\Gamma \left(z\right)$, не имеет нулей .

Объем с n -эллипсоида радиусами r ₁ , …, r _n можно выразить как

$$V_{n}(r_{1},\dotsc ,r_{n})={\frac {\pi ^{\frac {n}{2}}}{\Pi \left({\frac {n}{2}}\right)}}\prod _{k=1}^{n}r_{k}.$$

Связь с другими функциями

• В первом интеграле выше, который определяет гамма-функцию, пределы интегрирования фиксированы. Верхняя и нижняя неполные гамма-функции — это функции, полученные путем изменения нижнего или верхнего (соответственно) предела интегрирования.
• Гамма-функция связана с бета-функцией формулой
  $$\mathrm {B} (z_{1},z_{2})=\int _{0}^{1}t^{z_{1}-1}(1-t)^{z_{2}-1}\,dt={\frac {\Gamma (z_{1})\,\Gamma (z_{2})}{\Gamma (z_{1}+z_{2})}}.$$
• Логарифмическая производная гамма-функции называется дигамма-функцией ; высшие производные – это полигамма-функции .
• Аналогом гамма-функции над конечным полем или конечным кольцом являются гауссовы суммы , разновидность экспоненциальной суммы .
• Обратная гамма-функция представляет собой целую функцию и изучалась как отдельная тема.
• Гамма-функция также проявляется в важной связи с дзета-функцией Римана : $\zeta (z)$.
  $$\pi ^{-{\frac {z}{2}}}\;\Gamma \left({\frac {z}{2}}\right)\zeta (z)=\pi ^{-{\frac {1-z}{2}}}\;\Gamma \left({\frac {1-z}{2}}\right)\;\zeta (1-z).$$
  Он также появляется в следующей формуле:
  $$\zeta (z)\Gamma (z)=\int _{0}^{\infty }{\frac {u^{z}}{e^{u}-1}}\,{\frac {du}{u}},$$
  который действителен только для $\Re (z)>1$.
  Логарифм гамма-функции удовлетворяет следующей формуле Лерха:
  $$\log \Gamma (z)=\zeta _{H}'(0,z)-\zeta '(0),$$
  где $\zeta _{H}$ – дзета -функция Гурвица , $\zeta$ — дзета-функция Римана, а штрих ( ′ ) обозначает дифференцирование по первой переменной.
• Гамма-функция связана с растянутой экспоненциальной функцией . Например, моменты этой функции равны
  $$\langle \tau ^{n}\rangle \equiv \int _{0}^{\infty }t^{n-1}\,e^{-\left({\frac {t}{\tau }}\right)^{\beta }}\,\mathrm {d} t={\frac {\tau ^{n}}{\beta }}\Gamma \left({n \over \beta }\right).$$

Особые ценности

Основная статья: Частные значения гамма-функции

Некоторые конкретные значения гамма-функции, включая первые 20 цифр после десятичной точки:

$${\begin{array}{rcccl}\Gamma \left(-{\tfrac {3}{2}}\right)&=&{\tfrac {4{\sqrt {\pi }}}{3}}&\approx &+2.36327\,18012\,07354\,70306\\\Gamma \left(-{\tfrac {1}{2}}\right)&=&-2{\sqrt {\pi }}&\approx &-3.54490\,77018\,11032\,05459\\\Gamma \left({\tfrac {1}{2}}\right)&=&{\sqrt {\pi }}&\approx &+1.77245\,38509\,05516\,02729\\\Gamma (1)&=&0!&=&+1\\\Gamma \left({\tfrac {3}{2}}\right)&=&{\tfrac {\sqrt {\pi }}{2}}&\approx &+0.88622\,69254\,52758\,01364\\\Gamma (2)&=&1!&=&+1\\\Gamma \left({\tfrac {5}{2}}\right)&=&{\tfrac {3{\sqrt {\pi }}}{4}}&\approx &+1.32934\,03881\,79137\,02047\\\Gamma (3)&=&2!&=&+2\\\Gamma \left({\tfrac {7}{2}}\right)&=&{\tfrac {15{\sqrt {\pi }}}{8}}&\approx &+3.32335\,09704\,47842\,55118\\\Gamma (4)&=&3!&=&+6\end{array}}$$

(Эти цифры можно найти в OEIS . Представленные здесь значения усечены, а не округлены.)Комплекснозначная гамма-функция не определена для неположительных целых чисел, но в этих случаях значение может быть определено в сфере Римана как ∞ . Обратная гамма-функция и четко определена аналитична при этих значениях (и во всей комплексной плоскости ):

$${\frac {1}{\Gamma (-3)}}={\frac {1}{\Gamma (-2)}}={\frac {1}{\Gamma (-1)}}={\frac {1}{\Gamma (0)}}=0.$$

Лог-гамма-функция

Аналитическая функция log Γ( z )

Поскольку гамма-функции и факториал растут так быстро для умеренно больших аргументов, многие вычислительные среды включают функцию, возвращающую натуральный логарифм гамма-функции (часто называемую lgamma или lngamma в средах программирования или gammaln в электронных таблицах); он растет гораздо медленнее, а для комбинаторных вычислений позволяет складывать и вычитать журналы вместо умножения и деления очень больших значений. Его часто определяют как

$$\ln \Gamma (z)=-\gamma z-\ln z+\sum _{k=1}^{\infty }\left[{\frac {z}{k}}-\ln \left(1+{\frac {z}{k}}\right)\right].$$

Дигамма -функция , которая является производной этой функции, также часто встречается.В контексте технических и физических приложений, например, при распространении волн, функциональное уравнение

$$\ln \Gamma (z)=\ln \Gamma (z+1)-\ln z$$

Логарифмическая гамма-функция в комплексной плоскости от −2 − 2i до 2 + 2i с цветами

часто используется, поскольку позволяет определить значения функции в одной полосе шириной 1 по z из соседней полосы. В частности, начав с хорошего приближения для a z с большой действительной частью, можно шаг за шагом идти вниз к желаемому z . По указанию Карла Фридриха Гаусса Роктешель (1922) предложил $\ln(\Gamma (z))$ приближение для больших Re( z ) :

$$\ln \Gamma (z)\approx (z-{\tfrac {1}{2}})\ln z-z+{\tfrac {1}{2}}\ln(2\pi ).$$

Это можно использовать для точной аппроксимации ln(Γ( z )) для z с меньшим Re( z ) с помощью (PEBöhmer, 1939)

$$\ln \Gamma (z-m)=\ln \Gamma (z)-\sum _{k=1}^{m}\ln(z-k).$$

Более точное приближение можно получить, используя больше членов из асимптотических разложений ln(Γ( z )) и Γ( z ) , которые основаны на приближении Стирлинга.

$$\Gamma (z)\sim z^{z-{\frac {1}{2}}}e^{-z}{\sqrt {2\pi }}\left(1+{\frac {1}{12z}}+{\frac {1}{288z^{2}}}-{\frac {139}{51\,840z^{3}}}-{\frac {571}{2\,488\,320z^{4}}}\right)$$

как | г | → ∞ при постоянной | арг( z ) | < π . (См. последовательности A001163 и A001164 в OEIS .)

В более «естественном» изложении:

$$\ln \Gamma (z)=z\ln z-z-{\tfrac {1}{2}}\ln z+{\tfrac {1}{2}}\ln 2\pi +{\frac {1}{12z}}-{\frac {1}{360z^{3}}}+{\frac {1}{1260z^{5}}}+o\left({\frac {1}{z^{5}}}\right)$$

как | г | → ∞ при постоянной | арг( z ) | < π . (См. последовательности A046968 и A046969 в OEIS .)

Коэффициенты членов с k > 1 из z ^{1− к} в последнем расширении просто

$${\frac {B_{k}}{k(k-1)}}$$

где Bk _— числа Бернулли .

Гамма-функция также имеет ряд Стирлинга (выведенный Чарльзом Эрмитом в 1900 году), равный

$$\log \Gamma (1+x)={\frac {x(x-1)}{2!}}\log(2)+{\frac {x(x-1)(x-2)}{3!}}(\log(3)-2\log(2))+\cdots ,\quad \Re (x)>0.$$

Свойства

Теорема Бора -Моллерапа что среди всех функций, расширяющих факториалы до положительных действительных чисел, только гамма-функция является лог-выпуклой , то есть ее натуральный логарифм выпукл утверждает , на положительной вещественной оси. Другая характеристика дается теоремой Виланда .

Гамма-функция — это уникальная функция, которая одновременно удовлетворяет

1. $\Gamma (1)=1$,
2. $\Gamma (z+1)=z\Gamma (z)$ для всех комплексных чисел $z$ кроме неположительных целых чисел, и,
3. для целого числа n , ${\textstyle \lim _{n\to \infty }{\frac {\Gamma (n+z)}{\Gamma (n)\;n^{z}}}=1}$ для всех комплексных чисел $z$.

В определенном смысле функция ln(Γ) является более естественной формой; это проясняет некоторые внутренние атрибуты функции. Ярким примером является ряд Тейлора для ln(Γ) около 1:

$$\ln \Gamma (z+1)=-\gamma z+\sum _{k=2}^{\infty }{\frac {\zeta (k)}{k}}\,(-z)^{k}\qquad \forall \;|z|<1$$

где ζ ( k ) обозначает дзета-функцию Римана в точке k .

Итак, используя следующее свойство:

$$\zeta (s)\Gamma (s)=\int _{0}^{\infty }{\frac {t^{s}}{e^{t}-1}}\,{\frac {dt}{t}}$$

мы можем найти интегральное представление для функции ln(Γ) :

$$\ln \Gamma (z+1)=-\gamma z+\int _{0}^{\infty }{\frac {e^{-zt}-1+zt}{t\left(e^{t}-1\right)}}\,dt$$

или, установив z = 1 , чтобы получить интеграл для γ , мы можем заменить член γ его интегралом и включить его в приведенную выше формулу, чтобы получить:

$$\ln \Gamma (z+1)=\int _{0}^{\infty }{\frac {e^{-zt}-ze^{-t}-1+z}{t\left(e^{t}-1\right)}}\,dt\,.$$

Также существуют специальные формулы логарифма гамма-функции для рационального z . Например, если $k$ и $n$ являются целыми числами с $k<n$ и $k\neq n/2\,,$ затем

$${\begin{aligned}\ln \Gamma \left({\frac {k}{n}}\right)={}&{\frac {\,(n-2k)\ln 2\pi \,}{2n}}+{\frac {1}{2}}\left\{\,\ln \pi -\ln \sin {\frac {\pi k}{n}}\,\right\}+{\frac {1}{\pi }}\!\sum _{r=1}^{n-1}{\frac {\,\gamma +\ln r\,}{r}}\cdot \sin {\frac {\,2\pi rk\,}{n}}\\&{}-{\frac {1}{2\pi }}\sin {\frac {2\pi k}{n}}\cdot \!\int _{0}^{\infty }\!\!{\frac {\,e^{-nx}\!\cdot \ln x\,}{\,\cosh x-\cos(2\pi k/n)\,}}\,{\mathrm {d} }x\end{aligned}}$$

видеть. Эту формулу иногда используют для численных вычислений, поскольку подынтегральная функция убывает очень быстро.

Интегрирование по лог-гамме

Интеграл

$$\int _{0}^{z}\ln \Gamma (x)\,dx$$

может быть выражено через Барнса G -функцию ( Барнса см. в G -функции доказательство ):

$$\int _{0}^{z}\ln \Gamma (x)\,dx={\frac {z}{2}}\ln(2\pi )+{\frac {z(1-z)}{2}}+z\ln \Gamma (z)-\ln G(z+1)$$

где Re( z ) > −1 .

Это также можно записать через дзета-функцию Гурвица :

$$\int _{0}^{z}\ln \Gamma (x)\,dx={\frac {z}{2}}\ln(2\pi )+{\frac {z(1-z)}{2}}-\zeta '(-1)+\zeta '(-1,z).$$

Когда $z=1$ отсюда следует, что

$$\int _{0}^{1}\ln \Gamma (x)\,dx={\frac {1}{2}}\ln(2\pi ),$$

является следствием формулы Раабе и это также . О. Эспиноза и В. Молл вывели аналогичную формулу для интеграла от квадрата $\ln \Gamma$:

$$\int _{0}^{1}\ln ^{2}\Gamma (x)dx={\frac {\gamma ^{2}}{12}}+{\frac {\pi ^{2}}{48}}+{\frac {1}{3}}\gamma L_{1}+{\frac {4}{3}}L_{1}^{2}-\left(\gamma +2L_{1}\right){\frac {\zeta ^{\prime }(2)}{\pi ^{2}}}+{\frac {\zeta ^{\prime \prime }(2)}{2\pi ^{2}}},$$

где $L_{1}$ является ${\frac {1}{2}}\ln(2\pi )$.

Д.Х. Бэйли и его соавторы дал оценку за

$$L_{n}:=\int _{0}^{1}\ln ^{n}\Gamma (x)\,dx$$

когда $n=1,2$ в терминах дзета-функции Торнгейма–Виттена и ее производных.

Кроме того, известно также, что

$$\lim _{n\to \infty }{\frac {L_{n}}{n!}}=1.$$

Приближения

Сравнение гаммы (синяя линия) с факториалом (синие точки) и аппроксимацией Стирлинга (красная линия)

Комплексные значения гамма-функции можно аппроксимировать с помощью приближения Стирлинга или приближения Ланцоша .

$$\Gamma (z)\sim {\sqrt {2\pi }}z^{z-1/2}e^{-z}\quad {\hbox{as }}z\to \infty {\hbox{ in }}\left|\arg(z)\right|<\pi .$$

Это точно в том смысле, что отношение аппроксимации к истинному значению приближается к 1 в пределе | г | уходит в бесконечность.

Гамма-функция может быть вычислена с фиксированной точностью для $\operatorname {Re} (z)\in [1,2]$ применив интегрирование по частям к интегралу Эйлера. Для любого положительного числа x гамма-функция может быть записана

$${\begin{aligned}\Gamma (z)&=\int _{0}^{x}e^{-t}t^{z}\,{\frac {dt}{t}}+\int _{x}^{\infty }e^{-t}t^{z}\,{\frac {dt}{t}}\\&=x^{z}e^{-x}\sum _{n=0}^{\infty }{\frac {x^{n}}{z(z+1)\cdots (z+n)}}+\int _{x}^{\infty }e^{-t}t^{z}\,{\frac {dt}{t}}.\end{aligned}}$$

Когда Re( z ) ∈ [1,2] и $x\geq 1$, абсолютное значение последнего интеграла меньше, чем $(x+1)e^{-x}$. Выбрав достаточно большой $x$, это последнее выражение можно сделать меньше, чем $2^{-N}$ на любую желаемую стоимость $N$. Таким образом, гамма-функция может быть оценена как $N$ немного точности с приведенной выше серией.

Быстрый алгоритм вычисления гамма-функции Эйлера для любого алгебраического аргумента (в том числе рационального) был построен Е. А. Карацубой.

Для аргументов, которые являются целыми числами, кратными 1/24 конкретные гамма - функцию также можно быстро оценить с помощью среднеарифметико-геометрических итераций (см. значения гамма-функции ).

Практические реализации

В отличие от многих других функций, таких как нормальное распределение , для гамма-функции нет очевидной быстрой и точной реализации, которую легко реализовать. $\Gamma (z)$, легко находится. Поэтому стоит изучить возможные решения. Если скорость важна, а точность нет, опубликованные таблицы для $\Gamma (z)$ легко найти при поиске в Интернете, например, в онлайн-библиотеке Wiley можно использовать линейную интерполяцию . Большую точность можно получить при использовании кубической интерполяции за счет дополнительных вычислительных затрат. С $\Gamma (z)$ таблицы обычно публикуются для значений аргументов от 1 до 2, свойство $\Gamma (z+1)=z\ \Gamma (z)$ может использоваться для быстрого и легкого перевода всех реальных значений $z<1$ и $z>2$ в диапазон $1\leq z\leq 2$, так что только табличные значения $z$ необходимо использовать от 1 до 2.

Если интерполяционные таблицы нежелательны, то упомянутое выше приближение Ланцоша хорошо работает с точностью от 1 до 2 знаков для небольших, часто используемых значений z. Если приближение Ланцоша недостаточно точное, формулу Стерлинга для гамма-функции можно использовать . Более полное и точное решение аппроксимации Стерлинга можно найти на сайте Math2.org , оно воспроизведено ниже в терминах $\Gamma (z)$ за первые 8( $z^{0}{\text{ to }}z^{-7}$) условия. На основе экспериментальных данных в сравнении с известными значениями $\Gamma (z)$ для 1, 1,5 и 2 (1, ${\sqrt {\pi }}/2$и 1 соответственно), это решение имеет точность до 9 цифр для значений z выше 5 и 16 цифр для z выше 20. Меньшие значения z менее точны, но простой перевод $\Gamma (z)=\Gamma (z+1)/z$ может использоваться для легкого перевода более высоких и точных значений в более низкие значения, когда это необходимо. Менее точные потребности также можно удовлетворить, просто используя меньшее количество членов бесконечного ряда.

Асимптотический ряд Стирлинга для $\Gamma (z)$ используя первые 8 терминов:

$\Gamma (z)={\sqrt {2\pi /z}}{\Bigl (}z/e{\Big )}^{z}{\Bigl (}1+{\frac {1}{12z}}+{\frac {1}{288z^{2}}}-{\frac {139}{51840z^{3}}}-{\frac {571}{2488320z^{4}}}+{\frac {163879}{209018880z^{5}}}+{\frac {5246819}{75246796800z^{6}}}-{\frac {534703531}{902961561600z^{7}}}-...{\Bigl )}$

Приложения

Один автор описывает гамма-функцию как «возможно, наиболее распространенную специальную функцию или наименее «специальную» из них. Другие трансцендентные функции […] называются «специальными», потому что некоторых из них можно было бы избежать, избегая многих специализированные математические темы. С другой стороны, гамма-функции Γ( z ) . труднее всего избежать

Проблемы интеграции

Гамма-функция находит применение в таких разнообразных областях, как квантовая физика , астрофизика и гидродинамика . Гамма -распределение , формулируемое в терминах гамма-функции, используется в статистике для моделирования широкого круга процессов; например, время между возникновением землетрясений.

Основной причиной полезности гамма-функции в таких контекстах является преобладание выражений типа $f(t)e^{-g(t)}$ которые описывают процессы, которые экспоненциально затухают во времени или пространстве. Интегралы от таких выражений иногда можно решить через гамма-функцию, когда элементарного решения не существует. Например, если f — степенная функция, а g — линейная функция, простая замена переменных $u:=a\cdot t$ дает оценку

$$\int _{0}^{\infty }t^{b}e^{-at}\,dt={\frac {1}{a^{b}}}\int _{0}^{\infty }u^{b}e^{-u}d\left({\frac {u}{a}}\right)={\frac {\Gamma (b+1)}{a^{b+1}}}.$$

Тот факт, что интегрирование выполняется вдоль всей положительной действительной линии, может означать, что гамма-функция описывает кумуляцию зависящего от времени процесса, который продолжается бесконечно, или значение может быть суммой распределения в бесконечном пространстве.

Конечно, часто полезно использовать пределы интегрирования, отличные от 0 и ∞, для описания кумуляции конечного процесса, и в этом случае обычная гамма-функция больше не является решением; тогда решение называется неполной гамма-функцией . иногда называют полной гамма-функцией (Обычную гамма-функцию, полученную путем интегрирования по всей положительной действительной линии, для контраста .)

Важной категорией экспоненциально убывающих функций являются гауссовы функции.

$$ae^{-{\frac {(x-b)^{2}}{c^{2}}}}$$

и их интегралы, такие как функция ошибок . Между этими функциями и гамма-функцией существует множество взаимосвязей; в частности, фактор ${\sqrt {\pi }}$ получено путем оценки ${\textstyle \Gamma \left({\frac {1}{2}}\right)}$ является «то же самое», что и нормализующий коэффициент функции ошибок и нормального распределения .

Интегралы, которые мы обсуждали до сих пор, включают трансцендентные функции , но гамма-функция также возникает из интегралов чисто алгебраических функций. В частности, длины дуг эллипсов собой кривые , и лемнискат , которые представляют определяемые алгебраическими уравнениями, задаются эллиптическими интегралами , которые в особых случаях можно оценить с точки зрения гамма-функции. Гамма-функцию также можно использовать для расчета «объема» и «площади» гиперсфер - мерных n .

Расчет продуктов

Способность гамма-функции обобщать факториальные произведения сразу же приводит к ее приложениям во многих областях математики; в комбинаторике и, как следствие, в таких областях, как теория вероятностей и вычисление степенных рядов . Многие выражения, включающие произведения последовательных целых чисел, можно записать в виде некоторой комбинации факториалов, наиболее важным примером, возможно, является биномиальный коэффициент . Например, для любых комплексных чисел z и n с | г | < 1 , мы можем написать

$$(1+z)^{n}=\sum _{k=0}^{\infty }{\frac {\Gamma (n+1)}{k!\Gamma (n-k+1)}}z^{k},$$

который очень похож на биномиальный коэффициент, когда n является неотрицательным целым числом,

$$(1+z)^{n}=\sum _{k=0}^{n}{\frac {n!}{k!(n-k)!}}z^{k}=\sum _{k=0}^{n}{\binom {n}{k}}z^{k}.$$

Пример биномиальных коэффициентов объясняет, почему свойства гамма-функции при расширении до отрицательных чисел являются естественными. Биномиальный коэффициент дает количество способов выбрать k элементов из набора из n элементов; если k > n , то способов, конечно, нет. Если k > n , ( n - k )! является факториалом отрицательного целого числа и, следовательно, бесконечен, если мы используем определение факториалов гамма-функцией - деление на бесконечность дает ожидаемое значение 0.

Мы можем заменить факториал гамма-функцией, чтобы распространить любую такую ​​формулу на комплексные числа. Как правило, это работает для любого продукта, в котором каждый фактор является рациональной функцией индексной переменной путем факторизации рациональной функции в линейные выражения. Если P и Q монические полиномы степени m и n с соответствующими корнями p ₁ , …, pm _— и q ₁ , …, q _n , мы имеем

$$\prod _{i=a}^{b}{\frac {P(i)}{Q(i)}}=\left(\prod _{j=1}^{m}{\frac {\Gamma (b-p_{j}+1)}{\Gamma (a-p_{j})}}\right)\left(\prod _{k=1}^{n}{\frac {\Gamma (a-q_{k})}{\Gamma (b-q_{k}+1)}}\right).$$

Если у нас есть способ численного расчета гамма-функции, вычислить числовые значения таких продуктов очень просто. Количество гамма-функций в правой части зависит только от степени многочленов, поэтому не имеет значения, равно ли b − a 5 или 10. ⁵ . Приняв соответствующие пределы, можно сделать так, чтобы уравнение выполнялось, даже если левое произведение содержит нули или полюса.

Приняв пределы, некоторые рациональные продукты с бесконечным числом факторов также можно оценить с точки зрения гамма-функции. Благодаря теореме о факторизации Вейерштрасса аналитические функции могут быть записаны как бесконечные произведения, а иногда их можно представить как конечные произведения или факторы гамма-функции. Мы уже видели один яркий пример: формула отражения по сути представляет синусоидальную функцию как произведение двух гамма-функций. Исходя из этой формулы, показательная функция, а также все тригонометрические и гиперболические функции могут быть выражены через гамма-функцию.

Еще больше функций, включая гипергеометрическую функцию и ее частные случаи, могут быть представлены с помощью комплексных контурных интегралов от произведений и частных гамма-функции, называемых интегралами Меллина – Барнса .

Аналитическая теория чисел

Применением гамма-функции является изучение дзета-функции Римана . Фундаментальным свойством дзета-функции Римана является ее функциональное уравнение :

$$\Gamma \left({\frac {s}{2}}\right)\zeta (s)\pi ^{-{\frac {s}{2}}}=\Gamma \left({\frac {1-s}{2}}\right)\zeta (1-s)\pi ^{-{\frac {1-s}{2}}}.$$

Помимо прочего, это обеспечивает явную форму аналитического продолжения дзета-функции до мероморфной функции в комплексной плоскости и приводит к немедленному доказательству того, что дзета-функция имеет бесконечное количество так называемых «тривиальных» нулей на действительной прямой. Борвейн и др. назовите эту формулу «одним из самых прекрасных открытий математики». Еще одним претендентом на это звание может стать

$$\zeta (s)\;\Gamma (s)=\int _{0}^{\infty }{\frac {t^{s}}{e^{t}-1}}\,{\frac {dt}{t}}.$$

Обе формулы были выведены Бернхардом Риманом в его основополагающей статье 1859 года « Ueber die Anzahl der Primzahlen unter einer gegebenen Größe » («О числе простых чисел, меньших заданной величины»), ставшей одной из вех в развитии аналитической теории чисел . раздел математики, изучающий простые числа с помощью инструментов математического анализа.

История

Гамма-функция привлекла внимание некоторых из самых выдающихся математиков всех времен. Ее история, в частности задокументированная Филипом Дж. Дэвисом в статье, за которую он получил премию Шовене в 1963 году , отражает многие важные события в математике, начиная с 18 века. По словам Дэвиса, «каждое поколение нашло что-то интересное, что можно сказать о гамма-функции. Возможно, следующее поколение тоже это сделает».

век: Эйлер

Даниэля Бернулли Письмо Кристиану Гольдбаху , 6 октября 1729 г.

Проблема распространения факториала на нецелые аргументы, по-видимому, впервые рассматривалась Даниэлем Бернулли и Кристианом Гольдбахом в 1720-х годах. В частности, в письме Бернулли Гольдбаху от 6 октября 1729 г. Бернулли ввел представление произведения

$$x!=\lim _{n\to \infty }\left(n+1+{\frac {x}{2}}\right)^{x-1}\prod _{k=1}^{n}{\frac {k+1}{k+x}}$$

который хорошо определен для действительных значений x, отличных от отрицательных целых чисел.

Леонард Эйлер позже дал два разных определения: первое было не его интегралом, а бесконечным произведением , которое хорошо определено для всех комплексных чисел n , кроме отрицательных целых чисел:

$$n!=\prod _{k=1}^{\infty }{\frac {\left(1+{\frac {1}{k}}\right)^{n}}{1+{\frac {n}{k}}}}\,,$$

о чем он сообщил Гольдбаху в письме от 13 октября 1729 года. 8 января 1730 года он снова написал Гольдбаху, чтобы объявить о своем открытии интегрального представления.

$$n!=\int _{0}^{1}(-\ln s)^{n}\,ds\,,$$

что справедливо, когда действительная часть комплексного числа n строго больше -1 (т. е. $\Re (n)>-1$). Благодаря замене переменных t = −ln s это становится знакомым интегралом Эйлера. Эйлер опубликовал свои результаты в статье «De Progressionibus Transcententibus seu Quarum Termini Generales Alphaice Dari nequeunt» («О трансцендентных прогрессиях, т. е. тех, общие члены которых не могут быть заданы алгебраически»), представленной в Петербургскую Академию 28 ноября 1729 г. . Эйлер далее открыл некоторые важные функциональные свойства гамма-функции, включая формулу отражения.

Джеймс Стирлинг , современник Эйлера, также попытался найти непрерывное выражение для факториала и придумал то, что сейчас известно как формула Стирлинга . Хотя формула Стирлинга дает хорошую оценку n ! , также для нецелых чисел, он не дает точного значения. Расширения его формулы, исправляющие ошибку, были даны самим Стирлингом и Жаком Филиппом Мари Бине .

XIX век: Гаусс, Вейерштрасс и Лежандр

Первая страница статьи Эйлера

Карл Фридрих Гаусс переписал произведение Эйлера как

$$\Gamma (z)=\lim _{m\to \infty }{\frac {m^{z}m!}{z(z+1)(z+2)\cdots (z+m)}}$$

и использовал эту формулу для открытия новых свойств гамма-функции. Хотя Эйлер был пионером в теории комплексных переменных, он, похоже, не рассматривал факториал комплексного числа, как это впервые сделал Гаусс. Гаусс также доказал теорему умножения гамма-функции и исследовал связь между гамма-функцией и эллиптическими интегралами .

Карл Вейерштрасс далее установил роль гамма-функции в комплексном анализе , начиная с еще одного представления продукта:

$$\Gamma (z)={\frac {e^{-\gamma z}}{z}}\prod _{k=1}^{\infty }\left(1+{\frac {z}{k}}\right)^{-1}e^{\frac {z}{k}},$$

где γ — постоянная Эйлера–Машерони . Вейерштрасс изначально писал свой продукт как продукт, предназначенный для 1 / Γ , и в этом случае он берется по нулям функции, а не по ее полюсам. Вдохновленный этим результатом, он доказал то, что известно как факторизационная теорема Вейерштрасса — что любую целую функцию можно записать как произведение ее нулей в комплексной плоскости; обобщение основной теоремы алгебры .

Название гамма-функция и символ Γ были введены Адрианом-Мари Лежандром около 1811 года; Лежандр также переписал интегральное определение Эйлера в его современной форме. Хотя этот символ представляет собой греческую «гамму» в верхнем регистре, не существует общепринятого стандарта относительно того, следует ли писать имя функции «гамма-функция» или «гамма-функция» (некоторые авторы просто пишут « Γ -функция»). Альтернативное обозначение «пи-функции» Π( z ) = z ! из-за Гаусса иногда встречается в старой литературе, но обозначения Лежандра доминируют в современных произведениях.

Имеет смысл задаться вопросом, почему мы различаем «обычный факториал» и гамма-функцию, используя разные символы, и, в частности, почему гамма-функция должна быть нормализована к Γ( n + 1) = n ! вместо простого использования « Γ( n ) = n ! ». Учтите, что обозначения показателей степени x ^н , было обобщено с целых чисел на комплексные числа x ^С без каких-либо изменений. Мотивация Лежандра для нормализации, похоже, неизвестна, и некоторые критиковали ее как громоздкую (математик 20-го века Корнелиус Ланцос , например, назвал ее «лишенной всякой рациональности» и вместо этого использовал бы z ! ). Нормализация Лежандра упрощает некоторые формулы, но усложняет другие. С современной точки зрения лежандровая нормировка гамма-функции представляет собой интеграл аддитивного характера e ^{− х} против мультипликативного символа x ^С относительно меры Хаара ${\textstyle {\frac {dx}{x}}}$ на группе Ли R ⁺ . Таким образом, эта нормализация проясняет, что гамма-функция является непрерывным аналогом суммы Гаусса .

гамма-

Несколько проблематично то, что гамма-функции дано большое количество определений. Хотя они описывают одну и ту же функцию, доказать эквивалентность не совсем просто. Стирлинг так и не доказал, что его расширенная формула точно соответствует гамма-функции Эйлера; доказательство было впервые дано Чарльзом Эрмитом в 1900 году. Вместо того, чтобы искать специализированное доказательство для каждой формулы, было бы желательно иметь общий метод определения гамма-функции.

Одним из способов доказательства было бы найти дифференциальное уравнение , характеризующее гамма-функцию. Большинство специальных функций в прикладной математике возникают как решения дифференциальных уравнений, решения которых единственны. Однако гамма-функция, похоже, не удовлетворяет ни одному простому дифференциальному уравнению. Отто Гёльдер доказал в 1887 году, что гамма-функция, по крайней мере, не удовлетворяет никакому алгебраическому дифференциальному уравнению , показав, что решение такого уравнения не может удовлетворять рекуррентной формуле гамма-функции, что делает ее трансцендентно-трансцендентной функцией . Этот результат известен как теорема Гёльдера .

Определенная и общеприменимая характеристика гамма-функции не была дана до 1922 года. Затем Харальд Бор и Иоганнес Моллеруп доказали то, что известно как теорема Бора-Моллерупа : что гамма-функция является единственным решением факториального рекуррентного соотношения, которое является положительным и логарифмически выпуклая при положительном z и значение которой в точке 1 равно 1 (функция называется логарифмически выпуклой, если ее логарифм выпуклый). Другая характеристика дается теоремой Виланда .

Теорема Бора – Моллерупа полезна, поскольку относительно легко доказать логарифмическую выпуклость любой из различных формул, используемых для определения гамма-функции. Идя дальше, вместо того, чтобы определять гамма-функцию по какой-либо конкретной формуле, мы можем выбрать условия теоремы Бора-Моллерапа в качестве определения, а затем выбрать любую формулу, которая нам нравится, которая удовлетворяет этим условиям, в качестве отправной точки для изучения гамма-функции. . Этот подход использовала группа Бурбаки .

Борвейн и Корлесс обзор трех столетий работы над гамма-функцией.

Справочные таблицы и программное обеспечение

Хотя гамма-функцию можно вычислить практически так же легко, как и любую математически более простую функцию, с помощью современного компьютера — даже с помощью программируемого карманного калькулятора — это, конечно, не всегда так. До середины 20 века математики полагались на таблицы, сделанные вручную; в случае гамма-функции, в частности, таблица, рассчитанная Гауссом в 1813 году и таблица, вычисленная Лежандром в 1825 году.

руки график абсолютного значения комплексной гамма-функции из Таблиц высших функций Янке ] и Эмде .

Таблицы комплексных значений гамма-функции, а также нарисованные от руки графики были приведены в «Таблицах функций с формулами и кривыми» Янке , и Эмде , впервые опубликованных в Германии в 1909 году. По словам Майкла Берри «издание в J&E трехмерный график, показывающий полюса гамма-функции в комплексной плоскости, приобрел почти культовый статус».

На самом деле до 1930-х годов, когда в теоретической физике были обнаружены применения комплексной гамма-функции, практически не было никакой практической необходимости ни в чем, кроме реальных значений гамма-функции. Когда в 1950-х годах стали доступны электронные компьютеры для производства таблиц, для удовлетворения спроса было опубликовано несколько обширных таблиц для сложной гамма-функции, включая таблицу с точностью до 12 десятичных знаков от Национального бюро стандартов США .

Воспроизведение знаменитого сложного графика Янке и Эмде (Таблицы функций с формулами и кривыми, 4-е изд., Дувр, 1945 г.) гамма-функции от -4,5 - 2,5i до 4,5 + 2,5i.

Реализации гамма-функции с плавающей запятой двойной точности и ее логарифма теперь доступны в большинстве программного обеспечения для научных вычислений и библиотеках специальных функций, например TK Solver , Matlab , GNU Octave и GNU Scientific Library . Гамма-функция также была добавлена ​​в стандартную библиотеку C ( math.h ). Реализации произвольной точности доступны в большинстве систем компьютерной алгебры , таких как Mathematica и Maple . PARI/GP , MPFR и MPFUN содержат бесплатные реализации произвольной точности. В некоторых программных калькуляторах , например, в калькуляторе Windows и калькуляторе GNOME , функция факториала возвращает Γ( x + 1), если входное значение x не является целым числом.

См. также

• Восходящий факториал
• Интеграл Каэна – Меллина
• Эллиптическая гамма-функция
• постоянная Гаусса
• Псевдогамма-функция
• Гамма-функция Адамара
• Обратная гамма-функция
• Приближение Ланцоша
• Множественная гамма-функция
• Многомерная гамма-функция
• p -адическая гамма-функция
• Поххаммер к -символ
• q -гамма-функция
• Основная теорема Рамануджана
• Приближение Спуджа
• Приближение Стирлинга

Примечания

• Эта статья включает в себя материал из статьи Citizendium « Гамма-функция », которая лицензируется по лицензии Creative Commons Attribution-ShareAlike 3.0 Unported , но не по GFDL .

Дальнейшее чтение

• Абрамовиц, Милтон; Стегун, Ирен А., ред. (1972). «Глава 6» . Справочник по математическим функциям с формулами, графиками и математическими таблицами . Нью-Йорк: Дувр.
• Эндрюс, GE ; Аски, Р.; Рой, Р. (1999). «Глава 1 (Гамма- и Бета-функции)». Специальные функции . Нью-Йорк: Издательство Кембриджского университета. ISBN  978-0-521-78988-2 .
• Артин, Эмиль (2006). «Гамма-функция». В Розене, Майкл (ред.). Экспозиция Эмиля Артина: подборка . История математики. Том. 30. Провиденс, Род-Айленд: Американское математическое общество.
• Аски, Р. ; Рой, Р. (2010), «Гамма-функция» , в Олвере, Фрэнке У.Дж .; Лозье, Дэниел М.; Буасверт, Рональд Ф.; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям , издательство Кембриджского университета, ISBN  978-0-521-19225-5 , МР   2723248 .
• Биркгоф, Джордж Д. (1913). «Примечание о гамма-функции» . Бык. амер. Математика. Соц . 20 (1): 1–10. дои : 10.1090/s0002-9904-1913-02429-7 . МР   1559418 .
• Бёмер, П.Е. (1939). определенные интегралы Дифференциальные уравнения и Лейпциг: Кёлер Верлаг.
• Дэвис, Филип Дж. (1959). «Интеграл Леонарда Эйлера: исторический профиль гамма-функции». Американский математический ежемесячник . 66 (10): 849–869. дои : 10.2307/2309786 . JSTOR   2309786 .
• Пост, Эмиль (1919). «Обобщенные гамма-функции» . Анналы математики . Вторая серия. 20 (3): 202–217. дои : 10.2307/1967871 . JSTOR   1967871 . Проверено 5 марта 2021 г.
• Пресс, WH; Теукольский, С.А.; Феттерлинг, WT; Фланнери, BP (2007). «Раздел 6.1. Гамма-функция» . Численные рецепты: искусство научных вычислений (3-е изд.). Нью-Йорк: Издательство Кембриджского университета. ISBN  978-0-521-88068-8 .
• Роктешель, Орегон (1922). гамма-функции для аргументов Методы расчета сложных Дрезден: Технический университет Дрездена .
• Темме, Нико М. (1996). Специальные функции: введение в классические функции математической физики . Нью-Йорк: Джон Уайли и сыновья. ISBN  978-0-471-11313-3 .
• Уиттакер, ET ; Уотсон, Дж. Н. (1927). Курс современного анализа . Издательство Кембриджского университета. ISBN  978-0-521-58807-2 .

Внешние ссылки

• Цифровая библиотека математических функций NIST: Гамма-функция
• Паскаль Себа и Ксавье Гурдон. Введение в гамма-функцию . В форматах PostScript и HTML .
• Справочник по C++ для std::tgamma
• Примеры задач, связанных с гамма-функцией, можно найти на сайте exampleproblems.com .
• «Гамма-функция» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Оценщик гамма-функции Wolfram (произвольная точность)
• «Гамма» . Wolfram . Сайт функций
• Объем n-сфер и гамма-функция на MathPages