Лемниската постоянная

«Постоянная Гаусса» перенаправляется сюда. Чтобы узнать о параметре, используемом в орбитальной механике, см. Гравитационную постоянную Гаусса .

Лемниската Бернулли

В математике лемнискаты константа ϖ — трансцендентная математическая константа, представляющая собой отношение периметра лемнискаты к Бернулли ее диаметру , аналогично определению π для круга. Аналогично, периметр лемнискаты $(x^{2}+y^{2})^{2}=x^{2}-y^{2}$ составляет 2 ϖ . Константа лемниската тесно связана с эллиптическими функциями лемниската и примерно равна 2,62205755. Это также проявляется при оценке гамма- и бета-функций при определенных рациональных значениях. Символ ϖ является рукописным вариантом буквы π ; см. Пи § Вариант пи .

Иногда величины 2 ϖ или ϖ/2 называют константой лемнискаты .

По состоянию на 2024 год рассчитано более 1,2 триллиона цифр этой константы.

История

Постоянная Гаусса , обозначаемая G , равна ϖ / π ≈ 0,8346268. и назван в честь Карла Фридриха Гаусса , который вычислил его через среднее арифметико-геометрическое как $1/M{\bigl (}1,{\sqrt {2}}{\bigr )}$. К 1799 году у Гаусса было два доказательства теоремы о том, что $M{\bigl (}1,{\sqrt {2}}{\bigr )}=\pi /\varpi$ где $\varpi$ – константа лемнискаты.

Джон Тодд назвал еще две лемнискатные константы: первую лемнискатную константу A = ϖ /2 ≈ 1,3110287771 и вторую лемнискатную константу B = π /(2 ϖ ) ≈ 0,5990701173 .

Лемнискатная константа $\varpi$ и первая константа лемнискаты Тодда $A$ была доказана трансцендентность Карлом Людвигом Зигелем в 1932 году, а затем Теодором Шнайдером в 1937 году и второй лемнискатной константой Тодда. $B$ и постоянная Гаусса $G$ трансцендентность была доказана Теодором Шнайдером в 1941 году. В 1975 году Григорий Чудновский доказал, что множество $\{\pi ,\varpi \}$ независима алгебраически над $\mathbb {Q}$, что означает, что $A$ и $B$ также алгебраически независимы. Но набор ${\bigl \{}\pi ,M{\bigl (}1,1/{\sqrt {2}}{\bigr )},M'{\bigl (}1,1/{\sqrt {2}}{\bigr )}{\bigr \}}$ (где штрих обозначает производную по второй переменной) не является алгебраически независимым над $\mathbb {Q}$. Фактически,

$$\pi =2{\sqrt {2}}{\frac {M^{3}\left(1,{\frac {1}{\sqrt {2}}}\right)}{M'\left(1,{\frac {1}{\sqrt {2}}}\right)}}={\frac {1}{G^{3}M'\left(1,{\frac {1}{\sqrt {2}}}\right)}}.$$

В 1996 году Юрий Нестеренко доказал, что множество $\{\pi ,\varpi ,e^{\pi }\}$ алгебраически независима над $\mathbb {Q}$.

Формы

Обычно, $\varpi$ определяется первым равенством ниже.

$${\begin{aligned}\varpi &=2\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}={\sqrt {2}}\int _{0}^{\infty }{\frac {\mathrm {d} t}{\sqrt {1+t^{4}}}}=\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {t-t^{3}}}}=\int _{1}^{\infty }{\frac {\mathrm {d} t}{\sqrt {t^{3}-t}}}\\[6mu]&=4\int _{0}^{\infty }{\Bigl (}{\sqrt[{4}]{1+t^{4}}}-t{\Bigr )}\,\mathrm {d} t=2{\sqrt {2}}\int _{0}^{1}{\sqrt[{4}]{1-t^{4}}}\mathop {\mathrm {d} t} =3\int _{0}^{1}{\sqrt {1-t^{4}}}\,\mathrm {d} t\\[2mu]&=2K(i)={\tfrac {1}{2}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{2}}{\bigr )}={\tfrac {1}{2{\sqrt {2}}}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{4}}{\bigr )}={\frac {\Gamma (1/4)^{2}}{2{\sqrt {2\pi }}}}={\frac {2-{\sqrt {2}}}{4}}{\frac {\zeta (3/4)^{2}}{\zeta (1/4)^{2}}}\\[5mu]&=2.62205\;75542\;92119\;81046\;48395\;89891\;11941\ldots ,\end{aligned}}$$

где К — полный эллиптический интеграл первого рода с модулем к , В — бета-функция , Г — гамма-функция и z — дзета-функция Римана .

Константу лемнискаты также можно вычислить с помощью среднего арифметико-геометрического значения. $M$,

$$\varpi ={\frac {\pi }{M{\bigl (}1,{\sqrt {2}}{\bigr )}}}.$$

Более того,

$$e^{\beta '(0)}={\frac {\varpi }{\sqrt {\pi }}}$$

что аналогично

$$e^{\zeta '(0)}={\frac {1}{\sqrt {2\pi }}}$$

где $\beta$ – бета-функция Дирихле и $\zeta$ — дзета-функция Римана .

Константа лемнискаты равна

$$\varpi ={\tfrac {1}{2}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{2}}{\bigr )}$$

где В обозначает бета-функцию . Формула для тэта -функций Якоби имеет вид

$$\varpi =\pi \vartheta _{01}^{2}\left(e^{-\pi }\right)$$

Константа Гаусса обычно определяется как обратная величина среднего арифметико-геометрического числа 1 и квадратного корня из 2 после его вычисления $M{\bigl (}1,{\sqrt {2}}{\bigr )}$ опубликовано в 1800 году: $$G={\frac {1}{M{\bigl (}1,{\sqrt {2}}{\bigr )}}}$$Константы лемнискаты Джона Тодда можно выразить через бета-функцию B: $${\begin{aligned}A&={\frac {\varpi }{2}}={\tfrac {1}{4}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{2}}{\bigr )},\\[3mu]B&={\frac {\pi }{2\varpi }}={\tfrac {1}{4}}\mathrm {B} {\bigl (}{\tfrac {1}{2}},{\tfrac {3}{4}}{\bigr )}.\end{aligned}}$$

Ряд

Формулу Вьета для π можно записать:

$${\frac {2}{\pi }}={\sqrt {\frac {1}{2}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}}}\cdots$$

Аналогичная формула для ϖ :

$${\frac {2}{\varpi }}={\sqrt {\frac {1}{2}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\bigg /}\!{\sqrt {\frac {1}{2}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\Bigg /}\!{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\bigg /}\!{\sqrt {\frac {1}{2}}}}}}}\cdots$$

Произведение Уоллиса для π :

$${\frac {\pi }{2}}=\prod _{n=1}^{\infty }\left(1+{\frac {1}{n}}\right)^{(-1)^{n+1}}=\prod _{n=1}^{\infty }\left({\frac {2n}{2n-1}}\cdot {\frac {2n}{2n+1}}\right)={\biggl (}{\frac {2}{1}}\cdot {\frac {2}{3}}{\biggr )}{\biggl (}{\frac {4}{3}}\cdot {\frac {4}{5}}{\biggr )}{\biggl (}{\frac {6}{5}}\cdot {\frac {6}{7}}{\biggr )}\cdots$$

Аналогичная формула для ϖ :

$${\frac {\varpi }{2}}=\prod _{n=1}^{\infty }\left(1+{\frac {1}{2n}}\right)^{(-1)^{n+1}}=\prod _{n=1}^{\infty }\left({\frac {4n-1}{4n-2}}\cdot {\frac {4n}{4n+1}}\right)={\biggl (}{\frac {3}{2}}\cdot {\frac {4}{5}}{\biggr )}{\biggl (}{\frac {7}{6}}\cdot {\frac {8}{9}}{\biggr )}{\biggl (}{\frac {11}{10}}\cdot {\frac {12}{13}}{\biggr )}\cdots$$

Связанный результат для постоянной Гаусса ( $G=\varpi /\pi$) является:

$${\frac {\varpi }{\pi }}=\prod _{n=1}^{\infty }\left({\frac {4n-1}{4n}}\cdot {\frac {4n+2}{4n+1}}\right)={\biggl (}{\frac {3}{4}}\cdot {\frac {6}{5}}{\biggr )}{\biggl (}{\frac {7}{8}}\cdot {\frac {10}{9}}{\biggr )}{\biggl (}{\frac {11}{12}}\cdot {\frac {14}{13}}{\biggr )}\cdots$$

Бесконечный ряд, открытый Гауссом:

$${\frac {\varpi }{\pi }}=\sum _{n=0}^{\infty }(-1)^{n}\prod _{k=1}^{n}{\frac {(2k-1)^{2}}{(2k)^{2}}}=1-{\frac {1^{2}}{2^{2}}}+{\frac {1^{2}\cdot 3^{2}}{2^{2}\cdot 4^{2}}}-{\frac {1^{2}\cdot 3^{2}\cdot 5^{2}}{2^{2}\cdot 4^{2}\cdot 6^{2}}}+\cdots$$

Формула Мачина для π : ${\textstyle {\tfrac {1}{4}}\pi =4\arctan {\tfrac {1}{5}}-\arctan {\tfrac {1}{239}},}$ и несколько подобных формул для π можно получить, используя тождества суммы тригонометрических углов, например, формулу Эйлера ${\textstyle {\tfrac {1}{4}}\pi =\arctan {\tfrac {1}{2}}+\arctan {\tfrac {1}{3}}}$. Аналогичные формулы могут быть разработаны для ϖ , включая следующие, найденные Гауссом: ${\tfrac {1}{2}}\varpi =2\operatorname {arcsl} {\tfrac {1}{2}}+\operatorname {arcsl} {\tfrac {7}{23}}$, где $\operatorname {arcsl}$ — лемниската арксинус .

Константу лемнискаты можно быстро вычислить по ряду

$\varpi =2^{-1/2}\pi {\biggl (}\sum _{n\in \mathbb {Z} }e^{-\pi n^{2}}{\biggr )}^{2}=2^{1/4}\pi e^{-\pi /12}{\biggl (}\sum _{n\in \mathbb {Z} }(-1)^{n}e^{-\pi p_{n}}{\biggr )}^{2}$

где $p_{n}={\tfrac {1}{2}}(3n^{2}-n)$ (это обобщенные пятиугольные числа ). Также

$\sum _{m,n\in \mathbb {Z} }e^{-2\pi (m^{2}+mn+n^{2})}={\sqrt {1+{\sqrt {3}}}}{\dfrac {\varpi }{12^{1/8}\pi }}.$

В духе, аналогичном Базельской проблеме ,

$\sum _{z\in \mathbb {Z} [i]\setminus \{0\}}{\frac {1}{z^{4}}}=G_{4}(i)={\frac {\varpi ^{4}}{15}}$

где $\mathbb {Z} [i]$ являются гауссовскими целыми числами и $G_{4}$ - ряд Эйзенштейна веса ⁠ $4$⁠ ( см. в разделе «Лемнискатные эллиптические функции § Числа Гурвица» ). более общий результат

Соответствующий результат

$\sum _{n=1}^{\infty }\sigma _{3}(n)e^{-2\pi n}={\frac {\varpi ^{4}}{80\pi ^{4}}}-{\frac {1}{240}}$

где $\sigma _{3}$ представляет собой функцию суммы положительных делителей .

В 1842 году Мальмстен нашел

$\beta '(1)=\sum _{n=1}^{\infty }(-1)^{n+1}{\frac {\log(2n+1)}{2n+1}}={\frac {\pi }{4}}\left(\gamma +2\log {\frac {\pi }{\varpi {\sqrt {2}}}}\right)$

где $\gamma$ постоянная Эйлера и $\beta (s)$ — бета-функция Дирихле.

Константа лемнискаты определяется быстро сходящимся рядом

$$\varpi =\pi {\sqrt[{4}]{32}}e^{-{\frac {\pi }{3}}}{\biggl (}\sum _{n=-\infty }^{\infty }(-1)^{n}e^{-2n\pi (3n+1)}{\biggr )}^{2}.$$

Константа также определяется бесконечным произведением

$\varpi =\pi \prod _{m=1}^{\infty }\tanh ^{2}\left({\frac {\pi m}{2}}\right).$

Непрерывные дроби

(Обобщенная) цепная дробь для π равна $${\frac {\pi }{2}}=1+{\cfrac {1}{1+{\cfrac {1\cdot 2}{1+{\cfrac {2\cdot 3}{1+{\cfrac {3\cdot 4}{1+\ddots }}}}}}}}$$ Аналогичная формула для ϖ : $${\frac {\varpi }{2}}=1+{\cfrac {1}{2+{\cfrac {2\cdot 3}{2+{\cfrac {4\cdot 5}{2+{\cfrac {6\cdot 7}{2+\ddots }}}}}}}}$$

Определите Брункера непрерывную дробь с помощью $$b(s)=s+{\cfrac {1^{2}}{2s+{\cfrac {3^{2}}{2s+{\cfrac {5^{2}}{2s+\ddots }}}}}},\quad s>0.$$ Позволять $n\geq 0$ кроме первого равенства, где $n\geq 1$. Затем $${\begin{aligned}b(4n)&=(4n+1)\prod _{k=1}^{n}{\frac {(4k-1)^{2}}{(4k-3)(4k+1)}}{\frac {\pi }{\varpi ^{2}}}\\b(4n+1)&=(2n+1)\prod _{k=1}^{n}{\frac {(2k)^{2}}{(2k-1)(2k+1)}}{\frac {4}{\pi }}\\b(4n+2)&=(4n+1)\prod _{k=1}^{n}{\frac {(4k-3)(4k+1)}{(4k-1)^{2}}}{\frac {\varpi ^{2}}{\pi }}\\b(4n+3)&=(2n+1)\prod _{k=1}^{n}{\frac {(2k-1)(2k+1)}{(2k)^{2}}}\,\pi .\end{aligned}}$$ Например, $${\begin{aligned}b(1)&={\frac {4}{\pi }}\\b(2)&={\frac {\varpi ^{2}}{\pi }}\\b(3)&=\pi \\b(4)&={\frac {9\pi }{\varpi ^{2}}}.\end{aligned}}$$

Простые цепные дроби

Простые цепные дроби для константы лемнискаты и связанных с ней констант включают $${\begin{aligned}\varpi &=[2,1,1,1,1,1,4,1,2,\ldots ],\\[8mu]2\varpi &=[5,4,10,2,1,2,3,29,\ldots ],\\[5mu]{\frac {\varpi }{2}}&=[1,3,4,1,1,1,5,2,\ldots ],\\[2mu]{\frac {\varpi }{\pi }}&=[0,1,5,21,3,4,14,\ldots ].\end{aligned}}$$

Интегралы

Геометрическое представление $\varpi /2$ и $\varpi /{\sqrt {2}}$

Постоянная лемнискаты ϖ связана с площадью под кривой $x^{4}+y^{4}=1$. Определение $\pi _{n}\mathrel {:=} \mathrm {B} {\bigl (}{\tfrac {1}{n}},{\tfrac {1}{n}}{\bigr )}$, вдвое больше площади в положительном квадранте под кривой $x^{n}+y^{n}=1$ является ${\textstyle 2\int _{0}^{1}{\sqrt[{n}]{1-x^{n}}}\mathop {\mathrm {d} x} ={\tfrac {1}{n}}\pi _{n}.}$ В квартическом случае ${\tfrac {1}{4}}\pi _{4}={\tfrac {1}{\sqrt {2}}}\varpi .$

В 1842 году Мальмстен обнаружил, что

$$\int _{0}^{1}{\frac {\log(-\log x)}{1+x^{2}}}\,dx={\frac {\pi }{2}}\log {\frac {\pi }{\varpi {\sqrt {2}}}}.$$

Более того, $$\int _{0}^{\infty }{\frac {\tanh x}{x}}e^{-x}\,dx=\log {\frac {\varpi ^{2}}{\pi }}$$

и

$$\int _{0}^{\infty }e^{-x^{4}}\,dx={\frac {\sqrt {2\varpi {\sqrt {2\pi }}}}{4}},\quad {\text{analogous to}}\,\int _{0}^{\infty }e^{-x^{2}}\,dx={\frac {\sqrt {\pi }}{2}},$$ разновидность интеграла Гаусса .

Константа лемнискаты появляется при вычислении интегралов

$${\frac {\pi }{\varpi }}=\int _{0}^{\frac {\pi }{2}}{\sqrt {\sin(x)}}\,dx=\int _{0}^{\frac {\pi }{2}}{\sqrt {\cos(x)}}\,dx$$

$${\frac {\varpi }{\pi }}=\int _{0}^{\infty }{\frac {dx}{\sqrt {\cosh(\pi x)}}}$$

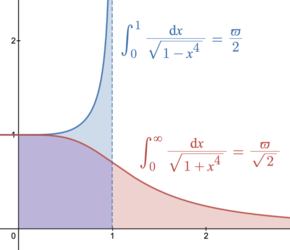
Константы лемнискаты Джона Тодда определяются интегралами:

$$A=\int _{0}^{1}{\frac {dx}{\sqrt {1-x^{4}}}}$$

$$B=\int _{0}^{1}{\frac {x^{2}\,dx}{\sqrt {1-x^{4}}}}$$

Окружность эллипса

Константа лемнискаты удовлетворяет уравнению

$${\frac {\pi }{\varpi }}=2\int _{0}^{1}{\frac {x^{2}\,dx}{\sqrt {1-x^{4}}}}$$

Эйлер открыл в 1738 году, что для прямоугольной эластики (первая и вторая константы лемнискаты)

$${\textrm {arc}}\ {\textrm {length}}\cdot {\textrm {height}}=A\cdot B=\int _{0}^{1}{\frac {\mathrm {d} x}{\sqrt {1-x^{4}}}}\cdot \int _{0}^{1}{\frac {x^{2}\mathop {\mathrm {d} x} }{\sqrt {1-x^{4}}}}={\frac {\varpi }{2}}\cdot {\frac {\pi }{2\varpi }}={\frac {\pi }{4}}$$

Теперь учитывая окружность $C$ эллипса с осями ${\sqrt {2}}$ и $1$, удовлетворяя $2x^{2}+4y^{2}=1$Стирлинг отметил, что

$${\frac {C}{2}}=\int _{0}^{1}{\frac {dx}{\sqrt {1-x^{4}}}}+\int _{0}^{1}{\frac {x^{2}\,dx}{\sqrt {1-x^{4}}}}$$

Следовательно, полная окружность равна

$$C={\frac {\pi }{\varpi }}+\varpi =3.820197789\ldots$$

Это также длина дуги синусоиды на половине периода:

$$C=\int _{0}^{\pi }{\sqrt {1+\cos ^{2}(x)}}\,dx$$

Другие ограничения

Аналогично $$2\pi =\lim _{n\to \infty }\left|{\frac {(2n)!}{\mathrm {B} _{2n}}}\right|^{\frac {1}{2n}}$$ где $\mathrm {B} _{n}$ являются числами Бернулли , мы имеем $$2\varpi =\lim _{n\to \infty }\left({\frac {(4n)!}{\mathrm {H} _{4n}}}\right)^{\frac {1}{4n}}$$ где $\mathrm {H} _{n}$ являются числами Гурвица .

Ссылки

• Вайсштейн, Эрик В. «Постоянная Гаусса» . Математический мир .
• Последовательности A014549, A053002 и A062539 в OEIS.
• Кокс, Дэвид А. (январь 1984 г.). «Среднее арифметико-геометрическое Гаусса» (PDF) . L'Enseignement Mathématique . 30 (2): 275–330. doi : 10.5169/seals-53831 . Проверено 25 июня 2022 г.

Внешние ссылки

• «Постоянная Гаусса и где она встречается» . www.johndcook.com . 17.10.2021.