Золотое сечение

Чтобы узнать о других значениях, см. Золотое сечение (значения) и Золотое число (значения) .

Золотое сечение ( φ )

Представительства
десятичный	1.618 033 988 749 894 ...
Алгебраическая форма	${\frac {1+{\sqrt {5}}}{2}}$
Непрерывная дробь	$1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}$

Золотой прямоугольник с длинной стороной a + b и короткой стороной a можно разделить на две части: аналогичный золотой прямоугольник (заштрихованный красным, справа) с длинной стороной a и короткой стороной b , и квадрат (закрашенный синим, слева) со сторонами длина а . Это иллюстрирует отношения а + б / а = а / б знак равно φ .

В математике две величины находятся в золотом сечении, если их отношение такое же, как отношение их суммы к большей из двух величин. Выражаясь алгебраически, для величин $a$ и $b$ с $a>b>0$, $a$ находится в золотом сечении $b$ если

${\frac {a+b}{a}}={\frac {a}{b}}=\varphi$

где греческая буква фи ( $\varphi$ или $\phi$) обозначает золотое сечение. Константа $\varphi$ удовлетворяет квадратному уравнению $\varphi ^{2}=\varphi +1$ и является иррациональным числом со значением

$\varphi ={\frac {1+{\sqrt {5}}}{2}}=$1.618 033 988 749 ....

Золотое сечение было названо крайним и средним Евклидом отношением . и божественная пропорция Луки Пачоли , а также носит несколько других имен.

Математики изучали свойства золотого сечения с древности. Это отношение диагонали правильного пятиугольника появляется при построении додекаэдра к его стороне и, таким образом , и икосаэдра . Золотой прямоугольник — то есть прямоугольник с соотношением сторон $\varphi$— можно разрезать на квадрат и прямоугольник меньшего размера с тем же соотношением сторон . Золотое сечение использовалось для анализа пропорций природных объектов и искусственных систем, таких как финансовые рынки , в некоторых случаях на основе сомнительного соответствия данным. Золотое сечение проявляется в некоторых закономерностях природы , включая спиральное расположение листьев и других частей растительности.

20-го века Некоторые художники и архитекторы , в том числе Ле Корбюзье и Сальвадор Дали , пропорции своих работ приближались к золотому сечению, полагая, что это эстетически приятно. Эти варианты использования часто появляются в форме золотого прямоугольника.

Расчет

Две величины $a$ и $b$ находятся в золотом сечении $\varphi$ если

${\frac {a+b}{a}}={\frac {a}{b}}=\varphi .$

Один из методов нахождения закрытой формы для $\varphi$ начинается с левой дроби. Упрощение дроби и замена обратной $b/a=1/\varphi$,

${\frac {a+b}{a}}={\frac {a}{a}}+{\frac {b}{a}}=1+{\frac {b}{a}}=1+{\frac {1}{\varphi }}.$

Поэтому,

$1+{\frac {1}{\varphi }}=\varphi .$

Умножение на $\varphi$ дает

$\varphi +1=\varphi ^{2}$

который можно переставить в

${\varphi }^{2}-\varphi -1=0.$

Квадратная формула дает два решения:

${\frac {1+{\sqrt {5}}}{2}}=1.618033\dots$ и ${\frac {1-{\sqrt {5}}}{2}}=-0.618033\dots .$

Потому что $\varphi$ представляет собой отношение между положительными величинами, $\varphi$ обязательно положительный корень. Отрицательный корень на самом деле является отрицательным обратным $-{\frac {1}{\varphi }}$, которое имеет много общих свойств с золотым сечением.

История

Смотрите также: Математика и искусство и число Фибоначчи § История

По словам Марио Ливио ,

Некоторые из величайших математических умов всех времен, от Пифагора и Евклида в древней Греции , средневекового итальянского математика Леонардо Пизанского и астронома эпохи Возрождения Иоганна Кеплера до современных научных деятелей, таких как оксфордский физик Роджер Пенроуз , проводили бесконечные часы. над этим простым соотношением и его свойствами. ... Биологи, художники, музыканты, историки, архитекторы, психологи и даже мистики размышляли и обсуждали причины его повсеместного распространения и привлекательности. На самом деле, вероятно, будет справедливо сказать, что золотое сечение вдохновляло мыслителей всех дисциплин, как никакое другое число в истории математики.

- Золотое сечение: история Фи, самого удивительного числа в мире

Древнегреческие математики впервые изучили золотое сечение из-за его частого появления в геометрии ; деление линии на «крайнее и среднее отношение» (золотое сечение) имеет важное значение в геометрии правильных пентаграмм и пятиугольников . Согласно одной из историй, математик 5-го века до нашей эры Гиппас обнаружил, что золотое сечение не является ни целым числом, ни дробью (оно иррационально ), удивив пифагорейцев . ( » Евклида В « Началах ок . 300 г. до н.э. ) представлено несколько положений и их доказательств с использованием золотого сечения: и содержит свое первое известное определение, которое выглядит следующим образом:

Говорят, что прямая линия разрезана в крайнем и среднем отношении, когда вся линия относится к большему отрезку, а большее к меньшему.

Майкл Мэстлин , первый, кто написал десятичную аппроксимацию соотношения

Золотое сечение изучалось периферийно в течение следующего тысячелетия. Абу Камиль (ок. 850–930) использовал его в своих геометрических расчетах пятиугольников и десятиугольников; его сочинения повлияли на сочинения Фибоначчи (Леонардо Пизанского) (ок. 1170–1250), который использовал это соотношение в связанных задачах геометрии, но не заметил, что оно связано с числами Фибоначчи .

Лука Пачоли назвал свою книгу «Божественная пропорция» ( 1509 ) в честь соотношения; книга, в значительной степени заимствованная у Пьеро делла Франчески , исследовала его свойства, включая его появление в некоторых платоновых телах . Леонардо да Винчи , иллюстрировавший книгу Пачоли, назвал это соотношение sectio aurea («золотое сечение»). Хотя часто говорят, что Пачоли выступал за применение золотого сечения для получения приятных, гармоничных пропорций, Ливио указывает, что интерпретация была связана с ошибкой 1799 года и что Пачоли фактически защищал витрувианскую систему рациональных пропорций. Пачоли также видел в этом соотношении католическое религиозное значение, что и привело к названию его работы. Математики 16-го века, такие как Рафаэль Бомбелли, решали геометрические задачи, используя соотношение.

Немецкий математик Саймон Якоб (ум. 1564) заметил, что последовательные числа Фибоначчи сходятся к золотому сечению ; это было заново открыто Иоганном Кеплером в 1608 году. Первое известное десятичное приближение (обратного) золотого сечения было заявлено как «около $0.6180340$» в 1597 году Михаэлем Мэстлином из Тюбингенского университета в письме Кеплеру, своему бывшему ученику. В том же году Кеплер написал Мэстлину о треугольнике Кеплера , который сочетает в себе золотое сечение с теоремой Пифагора . Кеплер сказал об этом:

У геометрии есть два великих сокровища: одно — теорема Пифагора, другое — деление прямой на экстремальное и среднее отношение. Первое мы можем сравнить с массой золота, второе мы можем назвать драгоценным камнем.

Математики восемнадцатого века Авраам де Муавр , Николай I Бернулли и Леонард Эйлер использовали формулу, основанную на золотом сечении, которая находит значение числа Фибоначчи на основе его положения в последовательности; в 1843 году она была заново открыта Жаком Филиппом Мари Бине , в честь которого она была названа «формулой Бине». Мартин Ом впервые использовал немецкий термин Goldener Schnitt («золотое сечение») для описания соотношения в 1835 году. Джеймс Салли использовал эквивалентный английский термин в 1875 году.

К 1910 году изобретатель Марк Барр начал использовать греческую букву фи ( $\varphi$) как символ золотого сечения. Он также был представлен тау ( $\tau$), первая буква древнегреческого τομή («разрез» или «раздел»).

Дэн Шехтман демонстрирует квазикристаллы в НИСТ в 1985 году, используя модель Зометоя .

Система построения зоме , разработанная Стивом Баером х годов, основана на системе симметрии икосаэдра в конце 1960 - / додекаэдра и повсеместно использует золотое сечение. Между 1973 и 1974 годами Роджер Пенроуз разработал мозаику Пенроуза — узор, связанный с золотым сечением как по соотношению площадей двух ромбических плиток, так и по их относительной частоте внутри узора. Это вызвало интерес после открытия Дэном Шехтманом, получившим Нобелевскую премию в 1982 году, квазикристаллов с икосаэдрической симметрией, которые вскоре были объяснены с помощью аналогий с мозаикой Пенроуза.

Математика

Иррациональность

Золотое сечение – иррациональное число . Ниже приведены два коротких доказательства иррациональности:

Противоречие от выражения в самых низких выражениях

Если бы φ было рациональным , то это было бы отношение сторон прямоугольника с целыми сторонами (прямоугольник, содержащий всю диаграмму). Но это также будет отношение целых сторон меньшего прямоугольника (самая правая часть диаграммы), полученного удалением квадрата. Последовательность уменьшения длин целых сторон, образованная удалением квадратов, не может продолжаться бесконечно, поскольку положительные целые числа имеют нижнюю границу, поэтому φ не может быть рациональным.

Это доказательство путем бесконечного спуска . Напомним, что:

целое — это длинная часть плюс короткая часть;
целое относится к более длинной части так же, как более длинная часть относится к более короткой части.

Если мы назовем все $n$ и более длинная часть $m,$ тогда второе утверждение выше становится

$n$ это $m$ как $m$ это $n-m.$

Сказать, что золотое сечение $\varphi$ рационально означает, что $\varphi$ это дробь $n/m$ где $n$ и $m$ являются целыми числами. Мы можем взять $n/m$ быть в самых низких условиях и $n$ и $m$ быть позитивным. Но если $n/m$ находится в самом низком выражении, то равноценное $m/(n-m)$ находится в еще более низких терминах. Это противоречие следует из предположения, что $\varphi$ является рациональным.

По иррациональности √ 5

Другое короткое доказательство – возможно, более широко известное – иррациональности золотого сечения использует замыкание рациональных чисел при сложении и умножении. Если $\varphi ={\tfrac {1}{2}}(1+{\sqrt {5}})$ рационально, то $2\varphi -1={\sqrt {5}}$ также рационально, что является противоречием, если уже известно, что квадратный корень всех неквадратных натуральных чисел иррационален.

Минимальный полином

Золотое сечение φ и его отрицательная обратная величина — φ ⁻¹ являются двумя корнями квадратного многочлена x ² - Икс - 1 . Отрицательное золотое сечение — φ и обратное φ. ⁻¹ являются двумя корнями квадратного многочлена x ² + Икс - 1 .

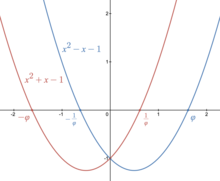
Золотое сечение также является алгебраическим числом и даже целым алгебраическим числом . Он имеет минимальный полином

$x^{2}-x-1.$

Этот квадратичный многочлен имеет два корня : $\varphi$ и $-\varphi ^{-1}.$

Золотое сечение также тесно связано с полиномом

$x^{2}+x-1,$

у которого есть корни $-\varphi$ и $\varphi ^{-1}.$ Золотое сечение, являющееся корнем квадратного многочлена, является конструктивным числом .

Сопряжение золотого сечения и степени

Сопряженный корень минимального многочлена $x^{2}-x-1$ является

$-{\frac {1}{\varphi }}=1-\varphi ={\frac {1-{\sqrt {5}}}{2}}=-0.618033\dots .$

Абсолютное значение этой величины ( $0.618\ldots$) соответствует соотношению длин, взятому в обратном порядке (более короткая длина сегмента к большей длине сегмента, $b/a$).

Это иллюстрирует уникальное свойство золотого сечения среди положительных чисел:

${\frac {1}{\varphi }}=\varphi -1,$

или его инверсия:

${\frac {1}{1/\varphi }}={\frac {1}{\varphi }}+1.$

Сопряженное и определяющее квадратично-полиномиальное отношение приводят к десятичным значениям, дробная часть которых совпадает с $\varphi$:

${\begin{aligned}\varphi ^{2}&=\varphi +1=2.618033\dots ,\\[5mu]{\frac {1}{\varphi }}&=\varphi -1=0.618033\dots .\end{aligned}}$

Последовательность полномочий $\varphi$ содержит эти значения $0.618033\ldots ,$ $1.0,$ $1.618033\ldots ,$ $2.618033\ldots ;$ в более общем смысле,любая сила $\varphi$ равен сумме двух непосредственно предшествующих степеней:

$\varphi ^{n}=\varphi ^{n-1}+\varphi ^{n-2}=\varphi \cdot \operatorname {F} _{n}+\operatorname {F} _{n-1}.$

В результате можно легко разложить любую степень $\varphi$ в кратное $\varphi$ и константа. Кратное и константа всегда являются соседними числами Фибоначчи. Это приводит к еще одному свойству положительных сил $\varphi$:

Если $\lfloor n/2-1\rfloor =m,$ затем:

${\begin{aligned}\varphi ^{n}&=\varphi ^{n-1}+\varphi ^{n-3}+\cdots +\varphi ^{n-1-2m}+\varphi ^{n-2-2m}\\[5mu]\varphi ^{n}-\varphi ^{n-1}&=\varphi ^{n-2}.\end{aligned}}$

Цепная дробь и квадратный корень

См. Также: Число Люка § Цепные дроби для степеней золотого сечения.

Приближения обратного золотого сечения конечными цепными дробями или отношениями чисел Фибоначчи.

Формула $\varphi =1+1/\varphi$ можно рекурсивно разложить, чтобы получить непрерывную дробь золотого сечения:

$\varphi =[1;1,1,1,\dots ]=1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}$

Фактически это простейшая форма цепной дроби, наряду с ее обратной формой:

$\varphi ^{-1}=[0;1,1,1,\dots ]=0+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}$

этих Подходящие дроби цепных дробей ( $1/1,$ $2/1,$ $2/1,$ $3/2,$ $5/3,$ $8/5,$ $13/8,$ ... или $1/1,$ $1/2,$ $2/3,$ $3/5,$ $5/8,$ $8/13,$ ...) являются отношениями последовательных чисел Фибоначчи . Постоянно малые члены ее непрерывной дроби объясняют, почему аппроксиманты сходятся так медленно. Это делает золотое сечение крайним случаем неравенства Гурвица для диофантовых приближений , которое утверждает, что для каждого иррационального $\xi$, существует бесконечно много различных дробей $p/q$ такой, что,

$\left|\xi -{\frac {p}{q}}\right|<{\frac {1}{{\sqrt {5}}q^{2}}}.$

Это означает, что константа ${\sqrt {5}}$ невозможно улучшить без исключения золотого сечения. Фактически, это наименьшее число, которое необходимо исключить, чтобы получить более точное приближение к таким числам Лагранжа .

Форма непрерывного квадратного корня для $\varphi$ можно получить из $\varphi ^{2}=1+\varphi$, что дает:

$\varphi ={\sqrt {1+{\sqrt {1+{\sqrt {1+\cdots }}}}}}.$

Связь с числами Фибоначчи и Люка

Дополнительная информация: число Фибоначчи § Связь с золотым сечением.

См. Также: Число Лукаса § Связь с числами Фибоначчи.

Спираль Фибоначчи (вверху), которая аппроксимирует золотую спираль , используя квадраты последовательности Фибоначчи размером до 21 . Другая аппроксимация золотой спирали создается (внизу) из сложенных квадратов, длины сторон которых представляют собой числа, принадлежащие последовательности чисел Люка , здесь до 76 .

Числа Фибоначчи и числа Люка имеют сложную связь с золотым сечением. В последовательности Фибоначчи каждое число равно сумме двух предыдущих, начиная с базовой последовательности. $0,1$:

$0,$ $1,$ $1,$ $2,$ $3,$ $5,$ $8,$ $13,$ $21,$ $34,$ $55,$ $89,$ $\ldots$( ОЭИС : A000045 ).

Последовательность чисел Люка (не путать с обобщенными последовательностями Люка , частью которых она является) похожа на последовательность Фибоначчи, в которой каждый член представляет собой сумму двух предыдущих, однако вместо этого начинается с $2,1$:

$2,$ $1,$ $3,$ $4,$ $7,$ $11,$ $18,$ $29,$ $47,$ $76,$ $123,$ $199,$ $\ldots$( ОЭИС : A000032 ).

В исключительных случаях золотое сечение равно пределу отношений последовательных членов последовательности Фибоначчи и последовательности чисел Люка:

$\lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}=\lim _{n\to \infty }{\frac {L_{n+1}}{L_{n}}}=\varphi .$

Другими словами, если число Фибоначчи и Люка делится на его непосредственного предшественника в последовательности, частное приблизительно равно $\varphi$.

Например, ${\frac {F_{16}}{F_{15}}}={\frac {987}{610}}=1.6180327\ldots ,$ и ${\frac {L_{16}}{L_{15}}}={\frac {2207}{1364}}=1.6180351\ldots .$

Эти приближения поочередно то ниже, то выше, чем $\varphi ,$ и сходиться к $\varphi$ по мере увеличения чисел Фибоначчи и Лукаса.

Выражения в закрытой форме для последовательностей Фибоначчи и Люка, включающие золотое сечение:

$F\left(n\right)={{\varphi ^{n}-(1-\varphi )^{n}} \over {\sqrt {5}}}={{\varphi ^{n}-(-\varphi )^{-n}} \over {\sqrt {5}}},$

$L\left(n\right)=\varphi ^{n}+(-\varphi )^{-n}=\left({1+{\sqrt {5}} \over 2}\right)^{n}+\left({1-{\sqrt {5}} \over 2}\right)^{n}\,.$

Объединив обе приведенные выше формулы, можно получить формулу для $\varphi ^{n}$ который включает в себя числа Фибоначчи и Люка:

$\varphi ^{n}={{L_{n}+F_{n}{\sqrt {5}}} \over 2}\,.$

Между числами Фибоначчи и Люка можно сделать вывод $L_{2n}=5F_{n}^{2}+2(-1)^{n}=L_{n}^{2}-2(-1)^{n},$ что упрощает выражение предела частного чисел Люка по числам Фибоначчи как равного квадратному корню из пяти :

$\lim _{n\to \infty }{\frac {L_{n}}{F_{n}}}={\sqrt {5}}.$

Действительно, верны гораздо более сильные утверждения:

$\vert L_{n}-{\sqrt {5}}F_{n}\vert ={\frac {2}{\varphi ^{n}}}\to 0,$

$(L_{3n}/2)^{2}=5(F_{3n}/2)^{2}+(-1)^{n}.$

Эти значения описывают $\varphi$ как фундаментальная единица поля алгебраических чисел $\mathbb {Q} ({\sqrt {5}})$.

Последовательные степени золотого сечения подчиняются повторяемости Фибоначчи , т.е. $\varphi ^{n+1}=\varphi ^{n}+\varphi ^{n-1}.$

Приведение к линейному выражению можно выполнить за один шаг, используя:

$\varphi ^{n}=F_{n}\varphi +F_{n-1}.$

Это тождество позволяет любому многочлену $\varphi$ свести к линейному выражению, например:

${\begin{aligned}3\varphi ^{3}-5\varphi ^{2}+4&=3(\varphi ^{2}+\varphi )-5\varphi ^{2}+4\\[5mu]&=3[(\varphi +1)+\varphi ]-5(\varphi +1)+4\\[5mu]&=\varphi +2\approx 3.618033.\end{aligned}}$

Последовательные числа Фибоначчи также можно использовать для получения аналогичной формулы золотого сечения, здесь путем бесконечного суммирования :

$\sum _{n=1}^{\infty }|F_{n}\varphi -F_{n+1}|=\varphi .$

В частности, полномочия $\varphi$ округляются до чисел Лукаса (по порядку, за исключением первых двух степеней, $\varphi ^{0}$ и $\varphi$, находятся в обратном порядке):

${\begin{aligned}\varphi ^{0}&=1,\\[5mu]\varphi ^{1}&=1.618033989\ldots \approx 2,\\[5mu]\varphi ^{2}&=2.618033989\ldots \approx 3,\\[5mu]\varphi ^{3}&=4.236067978\ldots \approx 4,\\[5mu]\varphi ^{4}&=6.854101967\ldots \approx 7,\end{aligned}}$

и так далее. Числа Лукаса также напрямую порождают степени золотого сечения; для $n\geq 2$:

$\varphi ^{n}=L_{n}-(-\varphi )^{-n}.$

В их взаимосвязи с золотым сечением лежит представление о том, что сумма третьих последовательных чисел Фибоначчи равна числу Люка, то есть $L_{n}=F_{n-1}+F_{n+1}$; и, что немаловажно, что $L_{n}={\frac {F_{2n}}{F_{n}}}$.

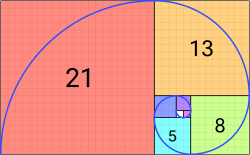
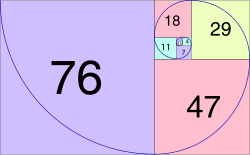
И последовательность Фибоначчи, и последовательность чисел Люка можно использовать для создания приблизительных форм золотой спирали (которая представляет собой особую форму логарифмической спирали ) с использованием четвертей круга с радиусами из этих последовательностей, лишь незначительно отличающимися от истинной золотой логарифмической спирали. спираль. Спираль Фибоначчи — это обычно термин, используемый для спиралей, которые аппроксимируют золотые спирали с использованием квадратов и четвертей кругов Фибоначчи.

Геометрия

Золотое сечение занимает видное место в геометрии. Например, он по своей сути участвует во внутренней симметрии пятиугольника и расширяется, образуя часть координат вершин правильного додекаэдра , а также вершин 5-ячеечного . Он также присутствует в треугольнике Кеплера и мозаике Пенроуза , а также в различных других многогранниках .

Строительство

Деление отрезка на внутреннее (вверху) и внешнее (внизу) разделение в соответствии с золотым сечением.

Разделение по внутреннему разделению

1. Наличие сегмента прямой $AB,$ построить перпендикуляр $BC$ в точку $B,$ с $BC$ половина длины $AB.$ Нарисуйте гипотенузу $AC.$
2. Нарисуйте дугу с центром $C$ и радиус $BC.$ Эта дуга пересекает гипотенузу $AC$ в точку $D.$
3. Нарисуйте дугу с центром $A$ и радиус $AD.$ Эта дуга пересекает исходный отрезок $AB$ в точку $S.$ Точка $S$ делит исходный сегмент прямой $AB$ на отрезки $AS$ и $SB$ с длиной в золотом сечении.

Деление внешним делением

1. Нарисуйте отрезок линии $AS$ и сконструировать не по делу $S$ сегмент $SC$ перпендикулярно $AS$ и той же длины, что и $AS.$
2. Разделите отрезок пополам $AS$ с $M.$
3. Круговая дуга вокруг $M$ с радиусом $MC$ пересекается в точке $B$ прямая линия через точки $A$ и $S$ (также известное как расширение $AS$). Соотношение $AS$ к построенному сегменту $SB$ это золотое сечение.

Примеры применения вы можете увидеть в статьях Пятиугольник с заданной длиной стороны , Декагон с заданной описанной окружностью и Десятиугольник с заданной длиной стороны .

Оба приведенных выше алгоритма создают геометрические конструкции , которые определяют два выровненных отрезка линии , где соотношение более длинного и более короткого является золотым сечением.

Золотой угол

Основная статья: Золотой угол

г ≈ 137,508°

Когда два угла, образующие полный круг, имеют размеры в золотом сечении, меньший из них называется золотым углом . ${\textstyle g\colon }$

${\begin{aligned}{\frac {2\pi -g}{g}}&={\frac {2\pi }{2\pi -g}}=\varphi ,\\[8mu]2\pi -g&={\frac {2\pi }{\varphi }}\approx 222.5^{\circ },\\[8mu]g&={\frac {2\pi }{\varphi ^{2}}}\approx 137.5^{\circ }.\end{aligned}}$

Этот угол возникает в моделях роста растений как оптимальное расстояние между побегами листьев вокруг стеблей растений, чтобы последующие листья не блокировали солнечный свет от листьев под ними.

Пятиугольная система симметрии

Пятиугольник и пентаграмма

Пентаграмма окрашена так, чтобы различать сегменты ее линий разной длины. Четыре длины находятся в золотом пропорции друг к другу.

В правильном пятиугольнике отношение диагонали к стороне является золотым сечением, а пересекающиеся диагонали разделяют друг друга в золотом сечении. Свойства золотого сечения правильного пятиугольника можно подтвердить, применив теорему Птолемея к четырехугольнику, образованному удалением одной из его вершин. Если длинная грань и диагонали четырехугольника равны $a,$ и короткие края $b,$ тогда теорема Птолемея дает $a^{2}=b^{2}+ab.$ Разделив обе части на $ab$ доходность (см. § Расчет выше),

${\frac {a}{b}}={\frac {a+b}{a}}=\varphi .$

Диагональные сегменты пятиугольника образуют пентаграмму с пятиконечной или многоугольник звездой , геометрия которого типично описывается формулой $\varphi$. Прежде всего, каждое пересечение ребер разделяет другие ребра в золотом сечении. Отношение длины более короткого сегмента к сегменту, ограниченному двумя пересекающимися краями (то есть стороне перевернутого пятиугольника в центре пентаграммы) равно $\varphi ,$ как показано на четырехцветной иллюстрации.

Пятиугольная и пентаграммная геометрия позволяют нам вычислить следующие значения для $\varphi$:

${\begin{aligned}\varphi &=1+2\sin(\pi /10)=1+2\sin 18^{\circ },\\[5mu]\varphi &={\tfrac {1}{2}}\csc(\pi /10)={\tfrac {1}{2}}\csc 18^{\circ },\\[5mu]\varphi &=2\cos(\pi /5)=2\cos 36^{\circ },\\[5mu]\varphi &=2\sin(3\pi /10)=2\sin 54^{\circ }.\end{aligned}}$

Золотой треугольник и золотой гномон

Основная статья: Золотой треугольник (математика)

Золотой треугольник ABC можно разделить биссектрисой на меньший золотой треугольник CXB и золотой гномон XAC .

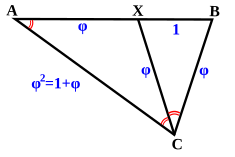
Треугольник, образованный двумя диагоналями и стороной правильного пятиугольника, называется золотым треугольником или возвышенным треугольником . Это остроугольный равнобедренный треугольник с углом при вершине 36° и углом при основании 72°. Две его равные стороны находятся в золотом пропорции к основанию. Треугольник, образованный двумя сторонами и диагональю правильного пятиугольника, называется золотым гномоном . Это тупоугольный равнобедренный треугольник с углом при вершине 108° и углем при основании 36°. Его основание находится в золотом пропорции к двум равным сторонам. Таким образом, пятиугольник можно разделить на два золотых гномона и центральный золотой треугольник. Пять вершин правильной пентаграммы представляют собой золотые треугольники. как и десять треугольников, образованных соединением вершин правильного десятиугольника с его центральной точкой.

Разделение одного из основных углов золотого треугольника пополам разделяет его на меньший золотой треугольник и золотой гномон. Аналогично любой остроугольный равнобедренный треугольник можно разделить на подобный треугольник и тупоугольный равнобедренный треугольник, но золотой треугольник — единственный, для которого это деление производится биссектрисой, потому что это единственный равнобедренный треугольник, угол при основании которого в два раза больше угол его вершины. Биссектриса золотого треугольника делит сторону, с которой он встречается, в золотом сечении, а площади двух разделенных частей также находятся в золотом сечении.

Если угол вершины золотого гномона разделить на три части , трисектор снова разделит его на меньший золотой гномон и золотой треугольник. Трисектор делит основание в золотом сечении, а площади двух частей соответствуют золотому сечению. Аналогично любой тупоугольный треугольник можно подразделить на подобный треугольник и остроугольный равнобедренный треугольник, но золотой гномон — единственный, для которого это подразделение производится трисектором угла, потому что это единственный равнобедренный треугольник, угол при вершине которого в три раза больше его базовый угол.

Мозаика Пенроуза

Основная статья: плитка Пенроуза

Плитки воздушного змея и дротика из мозаики Пенроуза. Цветные дуги делят каждое ребро в золотом сечении; когда две плитки имеют общий край, их дуги должны совпадать.

Золотое сечение занимает видное место в мозаике Пенроуза , семействе апериодических мозаик плоскости, разработанных Роджером Пенроузом , вдохновленным замечанием Иоганна Кеплера о том, что пентаграммы, декагоны и другие формы могут заполнять пробелы, которые оставляют только пятиугольные фигуры, сложенные вместе. Было изучено несколько вариантов этой мозаики, все прототипы которых демонстрируют золотое сечение:

• В оригинальной версии этой мозаики Пенроуза использовались четыре формы: правильные пятиугольники и пентаграммы, фигуры «лодочки» с тремя вершинами пентаграммы и ромбы в форме «ромба».
• В мозаике Пенроуза «воздушный змей и дротик» используются воздушные змеи с тремя внутренними углами 72 ° и одним внутренним углом 144 °, а также дротики, вогнутые четырехугольники с двумя внутренними углами 36 °, одним 72 ° и одним невыпуклым углом 216 °. . Специальные правила сопоставления ограничивают возможность пересечения плиток на любом ребре, в результате чего в любой вершине получается семь комбинаций плиток. И воздушные змеи, и дротики имеют стороны двух длин в золотом пропорции друг к другу. Площади этих двух форм плитки также находятся в золотом пропорции друг к другу.
• Воздушный змей и дротик можно разрезать по осям симметрии на пару золотых треугольников и золотых гномонов соответственно. При наличии подходящих правил сопоставления эти треугольники, называемые в данном контексте треугольниками Робинсона , могут использоваться в качестве прототипов для формы мозаики Пенроуза.
• Ромбическая мозаика Пенроуза содержит два типа ромба: тонкий ромб с углами 36° и 144° и толстый ромб с углами 72° и 108°. Все длины сторон равны, но отношение длин сторон к короткой диагонали в тонком ромбе равно $1:\varphi$, как и отношение сторон к длинной диагонали толстого ромба. Как и в случае с мозаикой из воздушного змея и дротика, площади двух ромбов находятся в золотом пропорции друг к другу. Опять же, эти ромбы можно разложить на пары треугольников Робинсона.

Оригинальная четырехплиточная плитка Пенроуза

Ромбическая плитка Пенроуза

В треугольниках и четырехугольниках

Строительство Одома

Конструкция Одома: AB : BC = AC : AB = φ : 1.

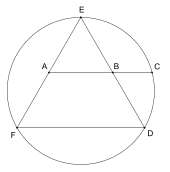
Джордж Одом нашел конструкцию для $\varphi$ с участием равностороннего треугольника : если отрезок, соединяющий середины двух сторон, продлен до пересечения описанной окружности , то две средние точки и точка пересечения с окружностью находятся в золотой пропорции.

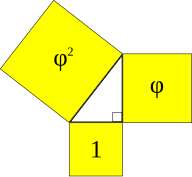
Треугольник Кеплера

Основная статья: треугольник Кеплера

Геометрическая прогрессия площадей квадратов на сторонах треугольника Кеплера

Равнобедренный треугольник, образованный из двух треугольников Кеплера, максимизирует отношение его внутреннего радиуса к длине стороны.

Треугольник Кеплера , названный в честь Иоганна Кеплера , представляет собой уникальный прямоугольный треугольник со сторонами в геометрической прогрессии :

$1\mathbin {:} {\sqrt {\varphi }}\mathbin {:} \varphi$.

Эти длины сторон являются тремя пифагорейскими средними двух чисел. $\varphi \pm 1$. Три квадрата по его сторонам имеют площади в золотой геометрической прогрессии. $1\mathbin {:} \varphi \mathbin {:} \varphi ^{2}$.

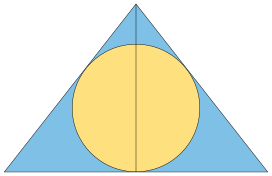
Среди равнобедренных треугольников соотношение внутреннего радиуса к длине стороны максимально для треугольника, образованного двумя отраженными копиями треугольника Кеплера, имеющими общую большую из двух сторон. Тот же равнобедренный треугольник максимизирует отношение радиуса полукруга в его основании к его периметру .

Для треугольника Кеплера с наименьшей длиной стороны $s$, площадь и острые внутренние углы равны:

${\begin{aligned}A&={\tfrac {s^{2}}{2}}{\sqrt {\varphi }},\\[5mu]\theta &=\sin ^{-1}{\frac {1}{\varphi }}\approx 38.1727^{\circ },\\[5mu]\theta &=\cos ^{-1}{\frac {1}{\varphi }}\approx 51.8273^{\circ }.\end{aligned}}$

Золотой прямоугольник

Основная статья: Золотой прямоугольник

Чтобы построить золотой прямоугольник с помощью линейки и циркуля за четыре простых шага:

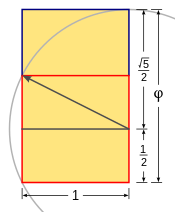
Нарисуйте квадрат.

Проведите линию от середины одной стороны квадрата к противоположному углу.

Используйте эту линию в качестве радиуса, чтобы нарисовать дугу, определяющую высоту прямоугольника.

Завершите золотой прямоугольник.

Золотое сечение определяет пропорции длин смежных сторон золотого прямоугольника в $1:\varphi$ соотношение. Складывание золотых прямоугольников создает золотые прямоугольники заново, а удаление или добавление квадратов из золотых прямоугольников оставляет прямоугольники по-прежнему пропорциональными. $\varphi$ соотношение. Они могут быть созданы с помощью золотых спиралей , последовательных квадратов и четвертей круга размером с число Фибоначчи и Люка. Они занимают видное место в икосаэдре, а также в додекаэдре (более подробно см. Раздел ниже).

Золотой ромб

Основная статья: Золотой ромб

Золотой ромб — это ромб , диагонали которого пропорциональны золотому сечению, чаще всего $1:\varphi$. Для ромба таких пропорций его острый и тупой углы равны:

${\begin{aligned}\alpha &=2\arctan {1 \over \varphi }\approx 63.43495^{\circ },\\[5mu]\beta &=2\arctan \varphi =\pi -\arctan 2=\arctan 1+\arctan 3\approx 116.56505^{\circ }.\end{aligned}}$

Длины его короткой и длинной диагоналей $d$ и $D$, по длине стороны $a$ являются:

${\begin{aligned}d&={2a \over {\sqrt {2+\varphi }}}=2{\sqrt {{3-\varphi } \over 5}}a\approx 1.05146a,\\[5mu]D&=2{\sqrt {{2+\varphi } \over 5}}a\approx 1.70130a.\end{aligned}}$

Его площадь, по $a$,и $d$:

${\begin{aligned}A&=(\sin(\arctan 2))~a^{2}={2 \over {\sqrt {5}}}~a^{2}\approx 0.89443a^{2},\\[5mu]A&={{\varphi } \over 2}d^{2}\approx 0.80902d^{2}.\end{aligned}}$

Его внутренний радиус , с точки зрения стороны $a$:

$r={\frac {a}{\sqrt {5}}}.$

Золотые ромбы образуют грани ромботриаконтаэдра , два золотых ромбоэдра , додекаэдр Билинского , и ромбический шестиконтаэдр .

Золотая спираль

Основная статья: Золотая спираль

Золотая спираль (красная) и ее приближение четвертькругами (зеленый) с перекрытием, показанным желтым цветом.

, Логарифмическая спираль радиус которой увеличивается на величину золотого сечения на каждые 108° поворота, окружающая вложенные золотые равнобедренные треугольники. Это другая спираль, отличная от золотой спирали , которая увеличивается на величину золотого сечения за поворот на 90°.

Логарифмические спирали — это самоподобные спирали, в которых расстояния, пройденные за оборот, находятся в геометрической прогрессии . Логарифмическая спираль, радиус которой увеличивается в раз золотого сечения на каждую четверть оборота, называется золотой спиралью . Эти спирали можно аппроксимировать четвертькругами, растущими по золотому сечению: или их приближения, полученные из чисел Фибоначчи, часто изображается вписанным в спиральный узор из квадратов, растущих в одинаковом соотношении. Точную логарифмическую форму золотой спирали можно описать полярным уравнением с $(r,\theta )$:

$r=\varphi ^{2\theta /\pi }.$

Не все логарифмические спирали связаны с золотым сечением, и не все спирали, связанные с золотым сечением, имеют ту же форму, что и золотая спираль. Например, другая логарифмическая спираль, заключающая в себе вложенную последовательность золотых равнобедренных треугольников, растет на золотое сечение на каждые 108 °, на которые она поворачивается, вместо угла поворота золотой спирали на 90 °. Другой вариант, называемый «лучшей золотой спиралью», увеличивается на золотое сечение за каждый пол-оборота, а не за каждую четверть оборота.

В додекаэдре и икосаэдре

координаты додекаэдра Декартовы :
(±1, ±1, ±1)
(0, ± φ , ± 1 / ж )
(± 1 / φ , 0, ± φ )
(± φ , ± 1 / ф , 0)
Вложенный куб внутри додекаэдра показан пунктирными линиями.

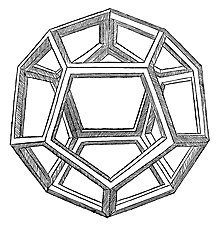
Правильный додекаэдр и его двойственный многогранник, икосаэдр , являются платоновыми телами , размеры которых связаны с золотым сечением. Додекаэдр имеет $12$ правильные пятиугольные грани, тогда как икосаэдр имеет $20$ равносторонние треугольники ; у обоих есть $30$ края .

Для додекаэдра со стороной $a$, радиус описанной и вписанной сферы, а также средний радиус равны ( $r_{u},$ $r_{i},$ и $r_{m},$ соответственно):

$r_{u}=a\,{\frac {{\sqrt {3}}\varphi }{2}},$ $r_{i}=a\,{\frac {\varphi ^{2}}{2{\sqrt {3-\varphi }}}},$ и $r_{m}=a\,{\frac {\varphi ^{2}}{2}}.$

А для икосаэдра стороны $a$, радиус описанной и вписанной сферы, а также средний радиус равны:

$r_{u}=a{\frac {\sqrt {\varphi {\sqrt {5}}}}{2}},$ $r_{i}=a{\frac {\varphi ^{2}}{2{\sqrt {3}}}},$ и $r_{m}=a{\frac {\varphi }{2}}.$

Объем и площадь поверхности додекаэдра можно выразить через $\varphi$:

$A_{d}={\frac {15\varphi }{\sqrt {3-\varphi }}}$ и $V_{d}={\frac {5\varphi ^{3}}{6-2\varphi }}$.

Также как и для икосаэдра:

$A_{i}=20{\frac {\varphi ^{2}}{2}}$ и $V_{i}={\frac {5}{6}}(1+\varphi ).$

Три золотых прямоугольника касаются всех 12 вершин правильного икосаэдра .

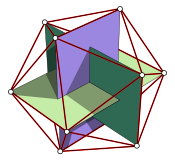
Эти геометрические значения можно вычислить по их декартовым координатам , которые также можно задать с помощью формул, включающих $\varphi$. Координаты додекаэдра показаны на рисунке выше, а координаты икосаэдра представляют собой циклические перестановки :

$(0,\pm 1,\pm \varphi )$, $(\pm 1,\pm \varphi ,0)$, $(\pm \varphi ,0,\pm 1).$

Наборы из трёх золотых прямоугольников пересекаются перпендикулярно внутри додекаэдров и икосаэдров, образуя кольца Борромео . В додекаэдрах пары противоположных вершин в золотых прямоугольниках встречаются с центрами пятиугольных граней, а в икосаэдрах — в их вершинах. В целом, три золотых прямоугольника содержат $12$ вершины икосаэдра или, что то же самое, пересекают центры $12$ граней додекаэдра.

Куб ; можно вписать в правильный додекаэдр, при этом некоторые диагонали пятиугольных граней додекаэдра служат рёбрами куба следовательно, длины ребер находятся в золотом сечении. Объем куба равен ${\tfrac {2}{2+\varphi }}$ раз больше, чем у додекаэдра. Фактически, золотые прямоугольники внутри додекаэдра находятся в золотых пропорциях к вписанному кубу, так что ребра куба и длинные ребра золотого прямоугольника сами находятся в $\varphi :\varphi ^{2}$ соотношение. С другой стороны, в октаэдр , который является двойственным многогранником куба, можно вписать икосаэдр, так что икосаэдр $12$ вершины касаются $12$ ребра октаэдра в точках, разделяющих его ребра в золотом сечении.

Другие многогранники связаны с додекаэдром и икосаэдром или их симметрией и, следовательно, имеют соответствующие отношения к золотому сечению. К ним относятся соединение пяти кубов , соединение пяти октаэдров , соединение пяти тетраэдров , соединение десяти тетраэдров , ромбический триаконтаэдр , икосододекаэдр , усеченный икосаэдр , усеченный додекаэдр и ромбокосододекаэдр , ромбический эннеаконтаэдр и многогранники Кеплера-Пуансо и ромбические h. экеконтаэдр . В четырех измерениях додекаэдр и икосаэдр выглядят как грани 120-ячеечной и 600-ячеечной граней , размеры которых снова связаны с золотым сечением.

Другие объекты недвижимости

золотого сечения Десятичное разложение можно рассчитать с помощью методов поиска корня, таких как метод Ньютона или метод Галлея , по уравнению $x^{2}-x-1=0$ или на $x^{2}-5=0$ (чтобы вычислить ${\sqrt {5}}$ первый). Время, необходимое для расчета $n$ цифры золотого сечения с использованием метода Ньютона по существу $O(M(n))$, где $M(n)$ это временная сложность умножения двух $n$-значные числа. Это значительно быстрее, чем известные алгоритмы для $\pi$ и $e$. Легко запрограммированная альтернатива, использующая только целочисленную арифметику, — вычислить два больших последовательных числа Фибоначчи и разделить их. Отношение чисел Фибоначчи $F_{25001}$ и $F_{25000},$ каждый более $5000$ цифры, выход более $10{,}000$ значащие цифры золотого сечения. Десятичное разложение золотого сечения $\varphi$ рассчитано с точностью до десяти триллионов ( $1\times 10^{13}=10{,}000{,}000{,}000{,}000$) цифры.

В комплексном плане пятые корни единства $z=e^{2\pi ki/5}$ (для целого числа ${\textstyle k}$) удовлетворение $z^{5}=1$ являются вершинами пятиугольника. Они не образуют кольцо квадратных целых чисел , однако сумма любого корня пятой степени из единицы и его комплексно-сопряженного числа $z+{\bar {z}},$ — квадратичное целое число, элемент ${\textstyle \mathbb {Z} [\varphi ].}$ Конкретно,

${\begin{aligned}e^{0}+e^{-0}&=2,\\[5mu]e^{2\pi i/5}+e^{-2\pi i/5}&=\varphi ^{-1}=-1+\varphi ,\\[5mu]e^{4\pi i/5}+e^{-4\pi i/5}&=-\varphi .\end{aligned}}$

Это справедливо и для остальных корней десятой степени из единицы, удовлетворяющих $z^{10}=1,$

${\begin{aligned}e^{\pi i}+e^{-\pi i}&=-2,\\[5mu]e^{\pi i/5}+e^{-\pi i/5}&=\varphi ,\\[5mu]e^{3\pi i/5}+e^{-3\pi i/5}&=-\varphi ^{-1}=1-\varphi .\end{aligned}}$

Для гамма-функции $\Gamma$, единственные решения уравнения $\Gamma (z-1)=\Gamma (z+1)$ являются $z=\varphi$ и $z=-\varphi ^{-1}$.

Когда золотое сечение используется в качестве основы системы счисления (см. основу золотого сечения , иногда называемую финарием или $\varphi$-nary ), квадратичные целые числа в кольце $\mathbb {Z} [\varphi ]$ – то есть числа вида $a+b\varphi$ для $a,b\in \mathbb {Z}$ – имеют конечные представления, но рациональные дроби имеют неконечные представления.

Золотое сечение также появляется в гиперболической геометрии как максимальное расстояние от точки на одной стороне идеального треугольника до ближайшей из двух других сторон: это расстояние, длина стороны равностороннего треугольника, образованного точками касания окружность, вписанная в идеальный треугольник, равна $4\log(\varphi ).$

в теории модулярных функций Золотое сечение появляется и . Для $\left|q\right|<1$, позволять

$R(q)={\cfrac {q^{1/5}}{1+{\cfrac {q}{1+{\cfrac {q^{2}}{1+{\cfrac {q^{3}}{1+\ddots }}}}}}}}.$

Затем

$R(e^{-2\pi })={\sqrt {\varphi {\sqrt {5}}}}-\varphi ,\quad R(-e^{-\pi })=\varphi ^{-1}-{\sqrt {2-\varphi ^{-1}}}$

и

$R(e^{-2\pi i/\tau })={\frac {1-\varphi R(e^{2\pi i\tau })}{\varphi +R(e^{2\pi i\tau })}}$

где $\operatorname {Im} \tau >0$ и $(e^{z})^{1/5}$ в цепной дроби следует оценивать как $e^{z/5}$. Функция $\tau \mapsto R(e^{2\pi i\tau })$ инвариантен относительно $\Gamma (5)$, конгруэнтная подгруппа модулярной группы . Также для положительных действительных чисел $a,b\in \mathbb {R} ^{+}$ и $ab=\pi ^{2},$ затем

${\begin{aligned}{\Bigl (}\varphi +R{{\bigl (}e^{-2a}{\bigr )}}{\Bigr )}{\Bigl (}\varphi +R{{\bigl (}e^{-2b}{\bigr )}}{\Bigr )}&=\varphi {\sqrt {5}},\\[5mu]{\Bigl (}\varphi ^{-1}-R{{\bigl (}{-e^{-a}}{\bigr )}}{\Bigr )}{\Bigl (}\varphi ^{-1}-R{{\bigl (}{-e^{-b}}{\bigr )}}{\Bigr )}&=\varphi ^{-1}{\sqrt {5}}.\end{aligned}}$

$\varphi$ — число Писо–Виджаярагавана .

Приложения и наблюдения

Видимые глазу ритмы: прямоугольники в соотношениях сторон φ (слева, посередине) и φ. ² (правая сторона) замостить квадрат.

Архитектура

Дополнительная информация: Математика и архитектура.

Швейцарский архитектор Ле Корбюзье , известный своим вкладом в современный международный стиль , сосредоточил свою философию дизайна на системах гармонии и пропорций. Вера Ле Корбюзье в математический порядок Вселенной была тесно связана с золотым сечением и рядом Фибоначчи, которые он описывал как «ритмы, видимые глазу и ясные в их отношениях друг с другом. И эти ритмы лежат в самой основе человеческой деятельности, они звучат в человеке органической неизбежностью, той самой прекрасной неизбежностью, которая вызывает выслеживание Золотого Сечения детьми, стариками, дикарями и учеными».

Ле Корбюзье явно использовал золотое сечение в своей Модулор системе масштаба для обозначения архитектурных пропорций . Он видел в этой системе продолжение давней традиции Витрувия » Леонардо да Винчи , « Витрувианского человека , работ Леона Баттисты Альберти и других, которые использовали пропорции человеческого тела для улучшения внешнего вида и функций архитектуры .

Помимо золотого сечения, Ле Корбюзье основывал систему на человеческих измерениях , числах Фибоначчи и двойной единице. Он довел идею золотого сечения в человеческих пропорциях до крайности: он разделил высоту своего модельного человеческого тела на уровне пупка на две части в золотом сечении, а затем разделил эти части в золотом сечении на колени и горло; он использовал эти пропорции золотого сечения в системе Модулора . Ле Корбюзье 1927 года Вилла Штайн в Гарше стала примером применения системы Modulor. Прямоугольный план, фасад и внутренняя структура виллы очень напоминают золотые прямоугольники.

Другой швейцарский архитектор, Марио Ботта , основывает многие свои проекты на геометрических фигурах. Несколько частных домов, которые он спроектировал в Швейцарии, состоят из квадратов и кругов, кубов и цилиндров. В доме, который он спроектировал в Ориглио , золотое сечение — это пропорция между центральной и боковыми частями дома.

Искусство

Дополнительная информация: Математика и искусство и История эстетики.

да Винчи Иллюстрация додекаэдра Пачоли » из «Божественной пропорции (1509 г.)

да Винчи Иллюстрации многогранников Леонардо Пачоли в «Божественной пропорции» заставили некоторых предположить, что он включил золотое сечение в свои картины. Но предположение о том, что его Мона Лиза , например, использует пропорции золотого сечения, не подтверждается собственными сочинениями Леонардо. Леонардо Точно так же, хотя Витрувианский человек часто изображается в связи с золотым сечением, пропорции фигуры на самом деле ему не соответствуют, и в тексте упоминаются только соотношения целых чисел.

Сальвадор Дали под влиянием работ Матилы Гики . явно использовал золотое сечение в своем шедевре «Таинство Тайной Вечери» . Размеры полотна – золотой прямоугольник. Огромный додекаэдр, в перспективе так, что края кажутся в золотом пропорции друг к другу, подвешен над Иисусом и позади него и доминирует в композиции.

Статистическое исследование 565 произведений искусства разных великих художников, проведенное в 1999 году, показало, что эти художники не использовали золотое сечение при определении размеров своих полотен. В результате исследования был сделан вывод, что среднее соотношение двух сторон изученных картин равно $1.34,$ средние значения для отдельных художников варьируются от $1.04$ (Гойя) чтобы $1.46$ (Беллини). С другой стороны, Пабло Тосто перечислил более 350 работ известных художников, в том числе более 100 с полотнами с золотым прямоугольником и ${\sqrt {5}}$ пропорции и другие с такими пропорциями, как ${\sqrt {2}},$ $3,$ $4,$ и $6.$

Изображение пропорций в средневековой рукописи. По словам Яна Чихольда : «Пропорции страницы 2:3. Пропорции полей 1:1:2:3. Пропорции текстовой области соответствуют золотому сечению».

Книги и дизайн

Основная статья: Каноны построения страниц

По словам Яна Чихольда ,

Было время, когда отклонения от поистине красивых пропорций страницы $2\mathbin {:} 3,$ $1\mathbin {:} {\sqrt {3}},$ и Золотое сечение были редкостью. Многие книги, выпущенные между 1550 и 1770 годами, показывают эти пропорции точно, с точностью до полмиллиметра.

Согласно некоторым источникам, золотое сечение используется в повседневном дизайне, например, в пропорциях игральных карт, открыток, плакатов, табличек с выключателями и широкоэкранных телевизоров.

Флаги

Флаг Того , соотношение сторон которого использует золотое сечение.

По словам его дизайнера, соотношение сторон (отношение ширины к высоте) флага Того должно было соответствовать золотому сечению.

Музыка

Эрно Лендвай анализирует работы Белы Бартока как основанные на двух противоположных системах: золотом сечении и акустической шкале . хотя другие музыковеды отвергают этот анализ. Французский композитор Эрик Сати использовал золотое сечение в нескольких своих произведениях, включая Sonneries de la Rose+Croix . Золотое сечение также проявляется в организации разделов музыки Дебюсси « Отражения в воде » из «Образов » (1-я серия, 1905), в которой «последовательность тональностей обозначена интервалы 34, 21, 13 и 8, а главная кульминация находится в позиции фи».

Музыковед Рой Ховат заметил, что формальные границы «Мера » Дебюсси точно соответствуют золотому сечению. Трезизе считает имеющиеся доказательства «замечательными», но предупреждает, что никакие письменные или зарегистрированные доказательства не позволяют предположить, что Дебюсси сознательно стремился к таким пропорциям.

Теоретики музыки, в том числе Ганс Зендер и Хайнц Болен, экспериментировали со шкалой 833 цента , музыкальной шкалой, основанной на использовании золотого сечения в качестве основного музыкального интервала . При измерении в центах (логарифмической шкале музыкальных интервалов) золотое сечение составляет примерно 833,09 цента.

Природа

Деталь блюдцеобразного растения Aeonium tabuliforme , демонстрирующая множественное спиральное расположение ( парастихия ).

Основная статья: Закономерности в природе

Смотрите также: число Фибоначчи § Природа

Иоганн Кеплер писал, что «образ мужчины и женщины проистекает из божественной пропорции. По моему мнению, размножение растений и репродуктивные действия животных находятся в одном и том же соотношении».

Психолог Адольф Цейзинг отметил, что золотое сечение появилось в филлотаксисе , и на основе этих закономерностей в природе доказал , что золотое сечение является универсальным законом. Цейзинг написал в 1854 году универсальный ортогенетический закон «стремления к красоте и полноте как в природе, так и в искусстве».

Однако некоторые утверждают, что многие очевидные проявления золотого сечения в природе, особенно в отношении размеров животных, являются вымышленными.

Физика

Квазиодномерный Изинга ферромагнетик ${\textstyle {\ce {CoNb2O6}}}$ (ниобат кобальта) имеет 8 предсказанных состояний возбуждения (с E ₈ симметрией ), которые при исследовании рассеяния нейтронов показали, что два самых низких состояния находятся в золотом сечении. В частности, эти квантовые фазовые переходы во время спинового возбуждения, которые происходят при температуре, близкой к абсолютному нулю, показали пары изломов в упорядоченной фазе и перевороты спина в парамагнитной фазе; обнаруживая, чуть ниже критического поля , спиновую динамику с резкими модами при низких энергиях, приближающихся к золотой середине.

Оптимизация

Не существует известного общего алгоритма равномерного расположения заданного количества узлов на сфере для любого из нескольких определений четного распределения (см., например, проблему Томсона или проблему Таммеса ). Однако полезным приближением является разделение сферы на параллельные полосы с одинаковой площадью поверхности и размещение одного узла в каждой полосе на расстоянии по долготе от золотого сечения круга, т.е. $360^{\circ }/\varphi \approx 222.5^{\circ }.$ Этот метод был использован для размещения 1500 зеркал студенческого спутника Starshine-3 .

является важнейшим элементом поиска золотого сечения Золотое сечение также .

Спорные наблюдения

Примеры спорных наблюдений золотого сечения включают следующее:

Раковины Наутилуса часто ошибочно называют золотыми.

• Часто утверждается, что определенные пропорции в телах позвоночных животных (включая человека) находятся в золотом сечении; например, соотношение последовательных фаланговых и пястных костей (костей пальцев), как говорят, приблизительно соответствует золотому сечению. Однако реальные показатели этих элементов у конкретных людей сильно различаются, и рассматриваемая пропорция часто значительно отличается от золотого сечения.
• раковины моллюсков, таких как наутилус, находятся в золотом сечении. Часто утверждается, что Рост раковин наутилуса следует логарифмической спирали , и иногда ошибочно утверждают, что любая логарифмическая спираль связана с золотым сечением. или иногда утверждали, что каждая новая камера имеет золотые пропорции по сравнению с предыдущей. Однако измерения раковин наутилусов не подтверждают это утверждение.
• Историк Джон Мэн утверждает, что и страницы, и текстовая область Библии Гутенберга «основаны на форме золотого сечения». Однако, по его собственным измерениям, соотношение высоты и ширины страниц $1.45.$
• Исследования психологов, начиная с Густава Фехнера ок. 1876 , были разработаны для проверки идеи о том, что золотое сечение играет роль в восприятии красоты человеком . Хотя Фехнер обнаружил, что предпочтение отдается пропорциям прямоугольников, основанным на золотом сечении, более поздние попытки тщательно проверить такую ​​гипотезу оказались в лучшем случае безрезультатными.
• При инвестировании некоторые специалисты по техническому анализу используют золотое сечение, чтобы указать на поддержку уровня цен или сопротивление росту цен на акции или товары; после значительных изменений цен вверх или вниз новые уровни поддержки и сопротивления предположительно находятся на уровне цен или вблизи них, связанных с начальной ценой через золотое сечение. Использование золотого сечения в инвестировании также связано с более сложными закономерностями, описываемыми числами Фибоначчи (например, волновой принцип Эллиотта и ретрейсмент Фибоначчи ). Однако другие аналитики рынка опубликовали анализы, показывающие, что эти проценты и закономерности не подтверждаются данными.

Египетские пирамиды

Великая пирамида Гизы

Великая пирамида в Гизе (также известная как пирамида Хеопса или Хуфу) была проанализирована пирамидологами двойной треугольник Кеплера как имеющая в поперечном сечении . Если бы эта теория была верна, золотое сечение описывало бы соотношение расстояний от середины одной из сторон пирамиды до ее вершины и от той же средней точки до центра основания пирамиды. Однако неточность измерения, вызванная отчасти удалением внешней поверхности пирамиды, не позволяет отличить эту теорию от других числовых теорий пропорций пирамиды, основанных на числах Пи или на соотношениях целых чисел. Современные ученые пришли к единому мнению, что пропорции этой пирамиды не основаны на золотом сечении, поскольку такая основа несовместима как с тем, что известно о египетской математике со времени строительства пирамиды, так и с египетскими теориями архитектуры и пропорций. использовал в других своих произведениях.

Парфенон

Утверждается, что многие пропорции Парфенона соответствуют золотому сечению, но это в значительной степени дискредитировано.

Некоторые говорят, что фасад Парфенона (ок. 432 г. до н. э.) , а также элементы его фасада и других мест ограничены золотыми прямоугольниками. Другие ученые отрицают, что у греков была какая-либо эстетическая связь с золотым сечением. Например, Кит Девлин говорит: «Конечно, часто повторяемое утверждение о том, что Парфенон в Афинах основан на золотом сечении, не подтверждается реальными измерениями. Фактически, вся история о греках и золотом сечении кажется необоснованной. " Мидхат Дж. Газале утверждает, что «только до Евклида… математические свойства золотого сечения были изучены».

Измерив 15 храмов, 18 монументальных гробниц, 8 саркофагов и 58 могильных стел с пятого века до нашей эры по второй век нашей эры, один исследователь пришел к выводу, что золотое сечение полностью отсутствовало в греческой архитектуре классической пятого века до нашей эры, и почти отсутствовал в течение следующих шести столетий. Более поздние источники, такие как Витрувий (первый век до н.э.), обсуждают исключительно пропорции, которые можно выразить целыми числами, то есть соизмеримые, а не иррациональные пропорции.

Современное искусство

Альберт Глейзес , Купальщицы (1912)

Секция d'Or («Золотое сечение») представляла собой коллектив художников , скульпторов, поэтов и критиков, связанных с кубизмом и орфизмом . Действуя примерно с 1911 по 1914 год, они приняли это название, чтобы подчеркнуть, что кубизм представляет собой продолжение великой традиции, а не изолированное движение, а также в знак уважения к математической гармонии, связанной с Жоржем Сёра . (Некоторые авторы утверждали, что Сёра использовал золотое сечение в своих картинах, но сочинения и картины Сёра предполагают, что он использовал простые целочисленные соотношения, и любое приближение золотого сечения было случайным.) Кубисты наблюдали в его гармонии, геометрической структурированности движения и формы, «примат идеи над природой», «абсолютную научную ясность замысла». ли золотое сечение в каких-либо композициях картины, представленные на знаменитой выставке Золотого салона Однако, несмотря на общий интерес к математической гармонии, труднее определить, использовало 1912 года. Ливио, например, утверждает, что это не так. и Марсель Дюшан сказал то же самое в интервью. С другой стороны, анализ показывает, что Хуан Грис использовал золотое сечение при создании произведений, которые, вероятно, но не окончательно, были показаны на выставке. Историк искусства Дэниел Роббинс утверждал, что название выставки не только отсылает к математическому термину, но и относится к более ранней группе Bandeaux d'Or , с которой Альберт Глез и другие бывшие члены аббатства Кретей . были связаны

Пит Мондриан широко использовал золотое сечение в своих геометрических картинах. Говорят, что хотя другие эксперты (в том числе критик Ив-Ален Буа ) опровергли эти утверждения.

См. также

• Список работ, оформленных с использованием золотого сечения
• Металлическое средство
• Пластиковое соотношение
• Сакральная геометрия
• Суперзолотое сечение
• Соотношение серебра

Ссылки

Цитируемые работы

• Герц-Фишлер, Роджер (1998) [1987]. Математическая история золотого числа . Дувр. ISBN  9780486400075 . (Первоначально называлась «Математическая история деления в экстремальном и среднем отношении ».)
• Ливио, Марио (2002). Золотое сечение: история Фи, самого удивительного числа в мире . Нью-Йорк: Бродвейские книги. ISBN  9780767908153 .
• Посаментье, Альфред С .; Леманн, Ингмар (2011). Славное золотое сечение . Книги Прометея . ISBN  9-781-61614-424-1 .

Дальнейшее чтение

• Дочи, Дьёрдь (1981). Сила ограничений: пропорциональная гармония в природе, искусстве и архитектуре . Бостон: Шамбала.
• Харгиттай, Иштван, изд. (1992). Пятикратная симметрия . Всемирная научная. ISBN  9789810206000 .
• Хантли, HE (1970). Божественная пропорция: исследование математической красоты . Нью-Йорк: Дувр. ISBN  978-0-486-22254-7 .
• Шааф, Уильям Л., изд. (1967). Золотая мера (PDF) . Серия переизданий группы по изучению математики Калифорнийской школы. Стэнфордский университет. Архивировано (PDF) из оригинала 25 апреля 2015 г.
• Ссимоне, Альдо (1997). Золотое сечение. Культурно-исторический лейтмотив математики . Палермо: Sigma Edizioni. ISBN  978-88-7231-025-0 .
• Вальзер, Ганс (2001) [ Золотое сечение, 1993]. Золотое сечение . Питер Хилтон пер. Вашингтон, округ Колумбия: Математическая ассоциация Америки. ISBN  978-0-88385-534-8 .

Внешние ссылки

• Вайсштейн, Эрик В. «Золотое сечение» . Математический мир .
• Богомольный, Александр (2018). «Золотое сечение в геометрии» . Разрезать узел .
• Нотт, Рон. «Соотношение золотого сечения: Фи» . Информация и деятельность профессора математики.
• «Миф, который не исчезнет» , Кейт Девлин , в котором рассматриваются многочисленные обвинения в использовании золотого сечения в культуре.
• Ложные золотые спирали, собранные Рэндаллом Манро
• Лекция на YouTube о проблеме мышей Зенона и логарифмических спиралях