Соединение пяти кубиков
| Соединение пяти кубиков | |
|---|---|
 ( Animation , 3D model ) | |
| Тип | Обычное соединение |
| Символ Коксетера | 2{5,3}[5{4,3}] [1] |
| звездообразования Ядро | ромбический триаконтаэдр |
| Выпуклая оболочка | Додекаэдр |
| Индекс | UCUC9 |
| Многогранники | 5 кубиков |
| Лица | 30 квадратов (видны как 360 треугольников ) |
| Края | 60 |
| Вершины | 20 |
| Двойной | Соединение пяти октаэдров |
| Группа симметрии | икосаэдрический ( I h ) |
| Подгруппа, ограничивающаяся одним компонентом | пиритоэдрический ( T h ) |
Соединение кубов пяти является одним из пяти правильных многогранных соединений. Впервые он был описан Эдмундом Гессом в 1876 году.
Это одно из пяти правильных соединений и двойственное соединению пяти октаэдров . Его можно рассматривать как огранку правильного додекаэдра.
Это одна звездочек ромботриаконтаэдра из . Он имеет икосаэдрическую симметрию ( I h ).
Геометрия [ править ]
Соединение представляет собой огранку додекаэдра (где можно увидеть пентаграммы, соответствующие пятиугольным граням). Каждый куб представляет собой выборку из 8 из 20 вершин додекаэдра.
 |  |  |  |
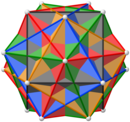| Виды с осей симметрии 2-го, 5-го и 3-го порядка. | |||
Если фигуру рассматривать как объединение пяти кубов, дающее простое невыпуклое тело без самопересекающихся поверхностей, то она имеет 360 граней (все треугольники ), 182 вершины (60 со степенью 3, 30 со степенью 4, 12 со степенью 5, 60 со степенью 8 и 20 со степенью 12) и 540 ребер, что дает эйлерову характеристику 182 - 540 + 360 = 2.
Расположение краев [ править ]
Его выпуклая оболочка представляет собой правильный додекаэдр . Кроме того, он разделяет расположение ребер с малым дитригональным икосододекаэдром , большим дитригональным икосододекаэдром и дитригональным додекадодекаэдром . Благодаря им он может образовывать многогранные соединения, которые также можно рассматривать как вырожденные однородные звездчатые многогранники; малый сложный ромбикосододекаэдр , большой сложный ромбикосододекаэдр и сложный ромбикосододекаэдр .
 Малый дитригональный икосододекаэдр |  Большой дитригональный икосододекаэдр |  Дитригональный додекадодекаэдр |
 Додекаэдр ( выпуклая оболочка ) |  Соединение пяти кубиков |  В виде сферической плитки |
Соединение десяти тетраэдров можно образовать, взяв каждый из этих пяти кубов и заменив их двумя тетраэдрами стеллы -октангула (которые имеют то же расположение вершин, что и куб).
Как созвездие [ править ]
 Желтая область соответствует одной грани куба. | Это соединение может образовываться в виде звездочки ромбического триаконтаэдра . |
См. также [ править ]
 |
Ссылки [ править ]
- ^ Правильные многогранники, стр.49-50, стр.98.
- Кромвель, Питер Р. (1997), Многогранники , Кембридж
{{citation}}: CS1 maint: отсутствует местоположение издателя ( ссылка ) . стр. 360 - Харман, Майкл Г. (около 1974 г.), Многогранные соединения , неопубликованная рукопись .
- Скиллинг, Джон (1976), «Однородные соединения однородных многогранников», Mathematical Proceedings of the Cambridge Philosophical Society , 79 (3): 447–457, Бибкод : 1976MPCPS..79..447S , doi : 10.1017/S0305004100052440 , MR 039755 4 , S2CID 123279687 .
- Канди Х. и Роллетт А. «Пять кубов в додекаэдре». §3.10.6 в Математических моделях , 3-е изд. Стрэдброк, Англия: Tarquin Pub., стр. 135–136, 1989.
- HSM Coxeter , Правильные многогранники , (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8 , 3.6 Пять правильных соединений , стр. 47-50, 6.2 Стеллирование платоновых тел , стр. 96-104
Внешние ссылки [ править ]
- MathWorld: Куб 5-Соединительный
- Джордж Харт: Соединения кубов
- Стивен Датч: Однородные многогранники и их двойники
- Клитцинг, Ричард. «3D соединение» .
 | Эта многогранникам, статья, посвященная незавершена . Вы можете помочь Википедии, расширив ее . |